в каком веке появились термины комбинаторика вероятность

История комбинаторики

История комбинаторики освещает развитие комбинаторики — раздела конечной математики, который исследует в основном различные способы выборки заданного числа m элементов из заданного конечного множества: размещения, сочетания, перестановки, а также перечисление и смежные проблемы. Начав с анализа головоломок и азартных игр, комбинаторика оказалась исключительно полезной для решения практических задач почти во всех разделах математики. Кроме того, комбинаторные методы оказались полезными в статистике, генетике, лингвистике и многих других науках.

Содержание

Древний период

Средневековье

В XII веке индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями.

В Западной Европе ряд глубоких открытий в области комбинаторики сделали два еврейских исследователя, Авраам ибн Эзра (XII век) и Леви бен Гершом (он же Герсонид, XIV век). Ибн Эзра обнаружил симметричность биномиальных коэффициентов, а Герсонид дал явные формулы для их подсчёта и применения в задачах вычисления числа размещений и сочетаний.

Несколько комбинаторных задач содержит «Книга абака» (Фибоначчи, XIII век). Например, он поставил задачу найти наименьшее число гирь, достаточное для взвешивания любого товара весом от 1 до 40 фунтов.

Новое время

Джероламо Кардано написал математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Тарталья и Галилей. В историю зарождавшейся теории вероятностей вошла переписка заядлого игрока шевалье де Мерэ с Пьером Ферма и Блезом Паскалем, где были затронуты несколько тонких комбинаторных вопросов. Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.

В этот же период формируется терминология новой науки. Термин «сочетание» (combination) впервые встречается у Паскаля (1653, опубликован в 1665 году). Термин «перестановка» (permutation) употребил в указанной книге Якоб Бернулли (хотя эпизодически он встречался и раньше). Бернулли использовал и термин «размещение» (arrangement).

После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Абрахам де Муавр и Джеймс Стирлинг нашли формулы для аппроксимации факториала. [5]

Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера. Он детально рассмотрел, например, следующие проблемы:

Кроме перестановок и сочетаний, Эйлер изучал разбиения, а также сочетания и размещения с условиями.

Современное развитие

В начале XX века начала развиваться комбинаторная геометрия: были доказаны теоремы Минковского — Радона, Радона, Хелли, Юнга, Бляшке, а также строго доказана изопериметрическая теорема. На стыке топологии, анализа и комбинаторики были доказаны теоремы Борсука — Улама и Люстерника — Шнирельмана. Во второй четверти XX века были поставлены проблема Борсука и проблема Нелсона — Эрдёша — Хадвигера. В 1940-х годах оформилась теория Рамсея. Отцом современной комбинаторики считается Пал Эрдёш, который ввёл в комбинаторику вероятностный анализ. Внимание к конечной математике и, в частности, к комбинаторике значительно повысилось со второй половины XX века, когда появились компьютеры. Сейчас это чрезвычайно содержательная и быстроразвивающаяся область математики.

Источник

Комбинаторика

Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.

Содержание

Примеры комбинаторных конфигураций и задач

Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:

Примерами комбинаторных задач являются:

Разделы комбинаторики

Перечислительная комбинаторика

Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.

Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.

Типичным примером задач данного раздела является подсчёт количества перестановок. Другой пример — известная Задача о письмах.

Структурная комбинаторика

К данному разделу относятся некоторые вопросы теории графов, а также теории матроидов.

Экстремальная комбинаторика

Примером этого раздела может служить следующая задача: какова наибольшая размерность графа, удовлетворяющего определённым свойствам.

Теория Рамсея

Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее:

в группе из 6 человек всегда можно найти трёх человек, которые либо попарно знакомы друг с другом, либо попарно незнакомы.

В терминах структурной комбинаторики это же утверждение формулируется так:

в любом графе с 6 вершинами найдётся либо клика, либо независимое множество размера 3.

Вероятностная комбинаторика

Этот раздел отвечает на вопросы вида: какова вероятность присутствия определённого свойства у заданного множества.

Топологическая комбинаторика

Топологическая комбинаторика (англ.) применяет идеи и методы комбинаторики в топологии, при изучении дерева принятия решений, частично упорядоченных множеств, раскрасок графа и др.

Инфинитарная комбинаторика

Инфинитарная комбинаторика (англ.) — применение идей и методов комбинаторики к бесконечным (в том числе, несчётным) множествам.

Открытые проблемы

Комбинаторика, и в частности, теория Рамсея, содержит много известных открытых проблем, подчас с весьма несложной формулировкой. Например, неизвестно, при каком наименьшем N в любой группе из N человек найдутся 5 человек, либо попарно знакомых друг с другом, либо попарно незнакомых (хотя известно, что 49 человек достаточно). [1]

Исторический очерк

См. также

Примечания

Литература

Ссылки

КОМБИНАТОРИКА — КОМБИНАТОРИКА, и, жен. Раздел дискретной математики, изучающий всевозможные сочетания и расположения предметов. | прил. комбинаторный, ая, ое. К. анализ. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

КОМБИНАТОРИКА — раздел математики, где рассматриваются сочетания, размещения, перестановки элементов и связанные с ними задачи. Широко применяется при вероятностном моделировании геол. процессов. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н … Геологическая энциклопедия

комбинаторика — — [http://www.dunwoodypress.com/148/PDF/Biotech Eng Rus.pdf] Тематики биотехнологии EN combinatorics … Справочник технического переводчика

КОМБИНАТОРИКА — раздел математики, посвящённый решению задач выбора и расположения элементов из некоторого основного (обычно конечного) множества в соответствии с заданными правилами. Простейшими задачами К. являются перестановки, сочетания и размещения … Большая политехническая энциклопедия

комбинаторика — и; ж. [лат. combinare соединять] Раздел математики, изучающий все возможные способы простейших перестановок элементов, цифр, каких л. данных. * * * комбинаторика раздел математики, в котором изучаются простейшие «соединения». Перестановки … … Энциклопедический словарь

Комбинаторика — 1) то же, что математический Комбинаторный анализ. 2) Раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов… … Большая советская энциклопедия

Комбинаторика — ж. Раздел математики, изучающий различного рода соединения элементов: перестановки, сочетания, размещения. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

комбинаторика — комбинаторика, комбинаторики, комбинаторики, комбинаторик, комбинаторике, комбинаторикам, комбинаторику, комбинаторики, комбинаторикой, комбинаторикою, комбинаториками, комбинаторике, комбинаториках (Источник: «Полная акцентуированная парадигма… … Формы слов

Источник

Комбинаторика и теория вероятности

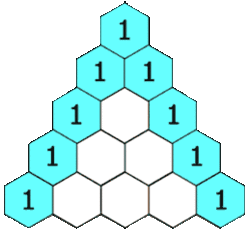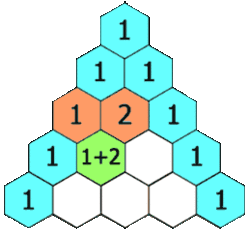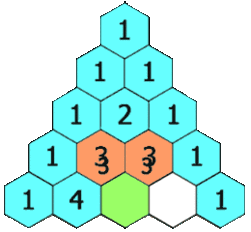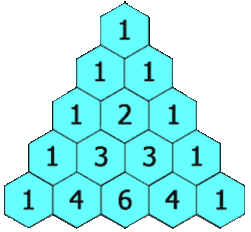
Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Нидийцы умели вычислять числа, которые сейчас называют «сочетания». В XII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из n слогов. Как научная дисциплина, комбинаторика сформировалась в XVII в. В книге «Теория и практика арифметики» (1656 г.) французский автор А. Также посвящает сочетаниям и перестановкам целую главу Б. Паскаль в «Трактате об арифметическом треугольнике» и в «Трактате о числовых порядках» (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин «комбинаторика» стал употребляться после опубликования Лейбницем в 1665 г. работы «Рассуждение о комбинаторном искусстве», в которой впервые было дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги «Ars conjectandi» (искусство предугадывания) в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в XIX веке.

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения

Комбинаторика – это раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составленной по заданным правилам.

Если исходное множество состоит из n различных элементов, то при каждом выборе мы будем извлекать из него новый элемент, отличный от всех других – это выбор без повторений.

Если исходное множество состоит из элементов k типов (классов), причём внутри каждого класса элементы неразличимы, то при очередном выборе мы можем извлечь либо новый элемент, либо такой, какой уже встречался при предшествующих извлечениях – это выбор с повторениями.

Иногда модель выбора с повторениями описывают по-другому. Полагают, что исходное множество содержит n различных элементов, но каждый элемент после его извлечения «записывается» в создаваемой комбинации и возвращается обратно в исходное множество. При этом каждый из n элементов может быть извлечён и «записан» неоднократно; число повторений зависит только от числа производимых извлечений. Такую модель называют также выбором с возвращением.

Извлечённые из исходного множества m элементов составляют выборку; из элементов выборки в соответствии с заданными правилами строится (или составляется) комбинация элементов.

Правило умножения. Пусть требуется выполнить одно за другим какие-то m действий. Если первое действие можно выполнить n1 способами, второе действие – n2 способами, третье – n3 способами и так до m-го действия, которое можно выполнить nm способами, то все m действий вместе могут быть выполнены n1× n2× n3×… nm способами.

Пример. Четыре мальчика и четыре девочки садятся на 8 расположенных подряд стульев, причём мальчики садятся на места с чётными номерами, а девочки – на места с нечётными номерами. Сколькими способами это можно сделать?

Решение: Первый мальчик может сесть на любое из четырёх чётных мест, второй – на любое из оставшихся трёх мест, третий – на любое из оставшихся двух мест. Последнему мальчику предоставляется всего одна возможность. Согласно правилу умножения, мальчики могут занять 4 места 4×3×2×1=24 способами. Столько же возможностей имеют и девочки. Таким образом, согласно правилу умножения, мальчики и девочки могут занять все стулья 24×24=576 способами.

Ответ: 576 способами.

Правило сложения. Если два действия взаимно исключают друг друга, причём одно из них можно выполнить m способами, а другое – n способами, то выполнить одно любое из этих действий можно m + n способами.

Пример. Имеется 20 тетрадей в линейку и 30 тетрадей в клетку. Необходимо выбрать две тетради одного вида. Сколько способов выбора двух тетрадей возможно, если учитывается порядок выбора тетрадей?

Решение: Условимся первым действием считать выбор тетрадей в линейку, вторым – выбор тетрадей в клетку. По правилу умножения две тетради в линейку можно выбрать 20×19=380 способами. Аналогично, две тетради в клетку можно выбрать 30×29=870 способами. Согласно условию задачи, следует выбрать две тетради одного вида. Таким образом, должно быть выполнено либо первое, либо второе, но не первое действие, а затем второе. Эти действия не могут быть выполнены одновременно. Поскольку они взаимно исключают друг друга. Поэтому общее число способов выбора тетрадей одного вида равно 380+870=1250.

1. В меню столовой предложено на выбор 5 первых, 8 вторых и 4 третьих блюда. Сколько различных вариантов обедов, состоящих из одного первого, одного второго и одного третьего блюда, можно составить из предложенного меню?

Решение: Согласно правилу умножения таких обедов можно составить 5×8×4 = 160.

Ответ: 160 вариантов обедов.

2. Миша забыл вторую и последнюю цифру пятизначного номера телефона друга. Какое наибольшее число звонков предстоит сделать Мише, если он решил перепробовать комбинации всех забытых цифр, чтобы в результате дозвониться до друга?

Решение: Второй и последней цифрой могут быть все 10 цифр. По правилу умножения получаем 10×10=100.

4. Девятиклассники Миша, Дима, Антон и Саша побежали на перемене к теннисному столу, за которым уже шла игра. Сколькими способами подбежавшие к столу четверо девятиклассников могут занять очередь для игры в настольный теннис?

Решение: Первым в очередь мог встать любой девятиклассник, вторым – любой из оставшихся троих, третьим – любой из оставшихся двоих и четвёртым – девятиклассник, подбежавший последним. По правилу умножения у четверых ребят существует 4×3×2×1=24 способа занять очередь.

5. Здание школы имеет 5 запасных выходов. Сколькими способами можно войти и выйти из здания школы?

Решение: По правилу умножения получаем 5×5=25 способов.

6. В городских соревнованиях по футболу участвовало 5 команд. Каждая

команда провела с каждой из остальных по одной игре на своём поле и по

одной игре на поле соперника. Сколько всего игр было сыграно?

Решение: Порядок выбора пары не имеет значения. Для каждой игры принимающую команду можно выбрать 5 способами, а команду гостей 4 способами; по правилу умножения общее количество игр равно 5×4=20 игр

7. В гардеробе у Алёши имеются брюки трёх цветов, свитера двух расцветок и ботинки двух цветов. Сколько существует всевозможных цветовых сочетаний брюк, свитера и ботинок у Алёши?

Решение: По правилу умножения получаем 3×2×2=12 сочетаний.

Ответ: 12 сочетаний.

8. Одновременно происходят выборы президента школьной детско-юношеской организации «СОТУР» и его заместителя. На должность президента выставили свои кандидатуры Лапина Юля, Губенко Юля, Осадчук Женя, а на должность заместителя – Малеванова Кристина, Явон Даша и Русалеева Даша. Сколько различных исходов выборов существует? В скольких вариантах будет кандидатура Малевановой Кристины?

Решение: По правилу умножения число различных исходов выборов равно 3×3=9. Кандидатура Малевановой Кристины будет в 3 вариантах.

Ответ: 9 исходов; 3 варианта.

9. У Любы есть любимый костюм, в котором она ходит в школу. Она надевает к нему белую, голубую, розовую или красную блузку, а в качестве «сменки» берёт босоножки или туфли. Кроме того, у Любы есть три разных бантика, подходящих ко всем блузкам. а) Сколько существует вариантов Любиной одежды? б) Сколько дней Люба сможет выглядеть по-новому в этом костюме? в) Сколько дней она будет ходить в туфлях? г) Сколько дней она будет ходить в красной блузке и босоножках?

Решение: а) По правилу умножения получаем: 4×2×3=24 варианта. б) по-новому будет выглядеть 24 дня. в) 12 дней (половина вариантов). г) 3 дня (так как будут меняться только бантики).

Ответ: а) 24 варианта; б) 24 дня; в) 12 дней; г) 3 дня.

10. Составляя расписание уроков на понедельник для 9 «Б» класса, завуч хочет первым уроком поставить либо физику, либо алгебру, а вторым – либо русский язык, либо литературу, либо историю, либо географию. Сколько существует вариантов составления расписания на первые два урока?

Решение: По правилу умножения получаем: 4×2=8 вариантов.

11. У Светланы три юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций из юбок и кофт имеется у Светланы?

Решение: По правилу умножения получаем: 3×5=15 комбинаций.

Ответ: 15 комбинаций.

12. Стас решил пойти на новогодний карнавал в костюме мушкетёра. В ателье проката ему предложили на выбор различные по фасону и цвету предметы: 3 пары брюк, 4 камзола, 3 шляпы, 2 пары сапог. Сколько различных карнавальных костюмов можно составить из этих предметов?

Решение: Общее количество предметов по правилу умножения равно: 3×4×3×2=72.

Ответ: 72 различных костюма.

13. Завуч составляет расписание уроков. В пятницу в 9 «Г» классе должно быть 6 уроков, причём обязательно один сдвоенный урок – алгебра. Сколько различных вариантов расписания уроков может составить завуч на пятницу, если 4 оставшихся урока она комбинирует из литературы, истории, биологии и физики?

Решение: Будем рассматривать сдвоенный урок как один урок, тогда всего нужно поставить в расписание 5 уроков. Первый урок можно выбрать из 5 вариантов, второй – из 4 вариантов, третий – из 3 вариантов, четвёртый – из 2 вариантов, а пятым поставить оставшийся урок. Общее число вариантов равно 5×4×3×2×1=120 вариантов.

Ответ: 120 вариантов.

14. На зачёте по алгебре будет пять задач – по одной из каждой пройденной темы. Задачи будут взяты из общего списка по 10 задач в каждой теме, а всего было пройдено 5 тем. При подготовке к зачёту Вова решил только по 8 задач в каждой теме. Найдите: а) общее число всех возможных вариантов зачётной работы; б) число тех вариантов, в которых Вова умеет решать все пять задач;

в) число тех вариантов, в которых Вова не сможет решить ни одной задачи;

г) число тех вариантов, в которых Вова умеет решать все задачи, кроме первой.

Решение: а) Первая задача может быть выбрана 10 способами, вторая тоже 10 (из задач другой темы), третья, четвёртая и пятая задачи также могут быть выбраны 10 способами каждая; по правилу умножения общее число всех возможных вариантов зачётной работы равно 10×10×10×10×10=100000. б) Число вариантов, в которых Вова умеет решать все пять задач равно 8×8×8×8×8=32768. в) Число вариантов, в которых Вова не сможет решить ни одной задачи равно 2×2×2×2×2=32. г) Число тех вариантов, в которых Вова умеет решать все задачи, кроме первой, равно 2×8×8×8×8=8192.

Ответ: а) 100000; б) 32768; в) 32; г) 8192.

1. Сколько существует четных пятизначных чисел, начинающихся нечетной цифрой?

2. На ферме есть 20 овец и 24 свиньи. Сколькими способами можно выбрать одну овцу и одну свинью? Если такой выбор уже сделан, сколькими способами можно сделать его еще раз?

3. Несколько стран в качестве символа своего государства решили использовать флаг в виде четырёх вертикальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зелёный. У каждой страны свой, отличный от других, флаг.

а) Сколько всего стран могут использовать такую символику?

б) Сколько всего стран могут использовать такую символику с верхней белой полосой?

в) Сколько всего стран могут использовать такую символику с нижней зелёной полосой?

Решение: а) 4*3*2*1 =24 страны, б) 6 стран (четвертая часть), в) 6 стран.

4. В школьной столовой на обед приготовили в качестве вторых блюд молочную кашу, плов и макароны. На сладкое – пирожное, фрукты, йогурт. Можно выбрать одно второе блюдо и одно блюдо на десерт. Сколько существует различных вариантов обеда?

Решение: 3*3=9 вариантов.

5. Имеются 10 различных точек, принадлежащих данной плоскости , причем никакие три из них не лежат на одной прямой. Сколько прямых можно провести через эти точки, если каждая из прямых проходит через две различные точки?

2) «Теория вероятностей».

В жизни под событием понимают любое явление, которое происходит или не происходит. Событиями являются и результаты испытаний (опытов), наблюдений и измерений. Все события можно разделить на невозможные, достоверные и случайные.

Невозможным называют событие, которое в данных условиях произойти не может.

Например: а) Петя родился 30 февраля;

б) вода в чайнике закипела при температуре 50°С.

Достоверным называют событие, которое в данных условиях обязательно произойдёт.

Например: а) после урока наступит перемена;

б) после воскресенья наступит будний день.

Случайным называют событие, которое в данных условиях может произойти, а может и не произойти.

Например: а) при телефонном звонке абонент оказался занят;

б) день рождения двух моих друзей – 15 марта.

События называются равновозможными, если по условию испытания нет оснований считать какое-либо из них более возможным, чем любое другое.

Рассмотрим группы событий:

1) «появление орла» и «появление решки» при одном бросании монеты;

2) «появление 1 очка», «появление 2 очков», …, «появление 6 очков» при одном бросании игральной кости;

3) «падение бутерброда маслом вверх» и «падение бутерброда маслом вниз»;

4) «изъятие из набора домино дубля» и «изъятие из набора домино костяшки с разными очками».

В примерах 1 и 2 нет оснований полагать, что в наступлении одного из событий есть какое-то преимущество (если монета и кубик правильные). Это равновозможные события. Часто равновозможность событий удаётся установить из соображений симметрии.

Примеры 3 и 4 демонстрируют образцы неравновозможных событий. Действительно, бутерброд чаще падает маслом вниз из-за того, что после намазывания хлеба маслом центр тяжести бутерброда смещается из центра его симметрии в сторону слоя масла. Дублей в наборе домино (пример 4) всего 7, а остальных костяшек 21.

Событие называется событием, противоположным событию А, если оно происходит, когда не происходит событие А.

Пример. Событию «все спортсмены команды завоевали призовые места» противоположным является событие «хотя бы один из спортсменов команды не занял призовое место».

Классическое определение вероятности

В повседневной жизни в разговоре часто используется слово «вероятный». Например, «к вечеру, вероятно, пойдёт дождь», «это невероятный случай», «вероятнее всего он опоздает». При употреблении этого слова интуитивно оценивается возможность наступления того или иного события. Можно сказать, что одно событие наступает чаще, чем другое. В этом случае говорят, что оно более возможно, т. е. его наступление более вероятно. Естественно. При такой оценке человеку помогает здравый смысл и жизненный опыт.

Вероятность события – это численная мера объективной возможности его появления.

Событие А называется благоприятствующим событию В, если появление события А влечёт за собой появление события В.

Пример. Событие А=<выбито 4 очка> является благоприятствующим событию В=<выбито менее 5 очков>.

Вероятность Р(А) наступления события А вычисляется как отношение числа исходов, благоприятствующих наступлению события, к числу всех исходов испытания.

Если N – число всех исходов испытания, а М – число исходов, благоприятствующих событию А, то .

1. Вероятность достоверного события равна 1: .

2. Вероятность невозможного события равна 0:

Теорема. Сумма вероятностей противоположных событий равна 1: .

Вероятность противоположного события находится по формуле: .

Пример. Вероятность попадания некоторым стрелком по бегущей мишени равна 0,8. какова вероятность того, что этот стрелок промахнётся, сделав выстрел?

Решение: Пусть событие А – попадание по мишени, тогда Р(А)=0,8. Событие — промах. = 1-Р(А)=1-0,8=0,2.Ответ: 0,2.

На практике – при изучении случайных явлений в естествознании, экономике, медицине, производстве – часто встречаются испытания, у которых число возможных исходов необозримо велико. А в ряде случаев до проведения реальных испытаний трудно или невозможно установить равновозможность исходов испытания. Поэтому, наряду с классическим, на практике используют так называемое статистическое определением вероятности. Чтобы выяснить, насколько вероятно то или иное случайное событие, связанное с экспериментом, нужно подсчитать, как часто оно происходит. Для этого используют две важные величины:

Относительной частотой события А в данной серии испытаний называют отношение числа испытаний М, в которых это событие произошло, к числу всех проведённых испытаний N, при этом число М называют абсолютной частотой или частотой события А.

Абсолютная частота показывает, сколько раз в серии экспериментов наблюдалось данное событие; относительная частота показывает, какая доля экспериментов завершилась наступлением данного события.

Относительную частоту события А обозначают , поэтому по определению: .

Пример. Во время тренировки в стрельбе по цели было сделано 30

выстрелов и зарегистрировано 26 попаданий. Какова относительная частота

попадания по цели в данной серии выстрелов?

Решение: Событие А – попадание по цели произошло в 26 случаях, т. е. М=26. Общее число испытаний N=30, поэтому =.

Ответ: .

Под статистической вероятностью понимают число, около которого колеблется относительная частота события при большом числе испытаний.

Невозможные, достоверные и случайные события

Для каждого из этих событий определить, каким оно является: невозможным, достоверным или случайным.

1. Из 26 учащихся класса двое справляют свой день рождения:января;июня.

Ответ: 1) случайное; 2) невозможное.

2. Случайным образом открывается художественное произведение и находится второе слово на левой странице. Это слово начинается: 1) с буквы М; 2) с буквы Ъ.

Ответ: 1) случайное; 2) невозможное.

3. Из списка журнала 9 класса (в котором есть и мальчики, и девочки) случайным образом выбран ученик: 1) это мальчик; 2) выбран ученик, которому 15 лет; 3) выбранному ученику 15 месяцев; 4) этому ученику больше двух лет.

Ответ: 1) случайное; 2) случайное; 3) невозможное.

Ответ: 1) невозможное; 2) достоверное.

5. В нашей школе учатся 758 учеников. Событие А=<в школе есть ученики с совпадающими днями рождения> является случайным или достоверным. Выясните, произошло ли это событие в вашем классе?

Ответ: Событие А – достоверное, так как количество учащихся школы 758>366 дней в году. Это событие случайное, так как количество учащихся нашего класса 26 человек.

6. Среди 150 билетов школьной благотворительной лотереи 30 выигрышных. Сколько билетов надо купить, чтобы событие А=<вы ничего не выиграете> было невозможным?

Ответ: 150-29=121 билет.

7. В 9 «Г» классе учится 16 мальчиков и 10 девочек. Какие из следующих событий являются невозможными, какие случайными, какие – достоверными:

А= <в классе есть два человека, родившихся в разные месяцы>;

В=<в классе есть два человека, родившихся в одном месяце>;

С=<в классе есть два мальчика, родившихся в одном месяце>;

D=<в классе есть две девочки, родившиеся в одном месяце>;

Е=<все мальчики родились в разные месяцы>;

F=<все девочки родились в разные месяцы>;

К=<есть мальчик и девочка, родившиеся в одном месяце>;

М= <есть мальчик и девочка, родившиеся в разные месяцы>.

Ответ: Событие А – случайное, событие В – достоверное, событие С – достоверное, событие D – случайное, событие Е – невозможное, событие F – случайное, событие K – случайное, событие M – случайное.

8. Около школы останавливаются автобусы трёх маршрутов, идущих в сторону лесозавода: № 5, № 13 и № 23. Интервал в движении автобусов каждого маршрута колеблется от 8 до 10 минут. Когда Саша, Маша, Кристина и Катя подошли к остановке, от неё отошёл автобус № 13, а ещё через 6 минут подошёл автобус № 5. После этого каждый из ребят высказал своё мнение о том, автобус какого маршрута будет следующим:

Саша: Следующим обязательно будет № 23.

Маша: Возможно, что следующим будет № 23.

Кристина: Возможно, что следующим будет № 13.

Катя: Невозможно, что следующим будет № 5.

С кем из ребят вы согласны, а с кем нет? Объясните сделанный выбор.

Ответ: Не прав только Саша.

9. На дорогу от дома до школы Миша тратит от 10 до 15 минут, если идёт пешком, и от 2 до 3 минут, если едет на автобусе. При каких интервалах движения автобусов событие А==<по пути в школу Мишу обгонит хотя бы один автобус> будет невозможным, при каких – случайным, при каких – достоверным?

Ответ: Больше 7 минут – случайным, меньше 7 минут – достоверным.

Совместные и несовместные события

1. В сыгранной Катей и Ларисой партии в шахматы: 1) Катя выиграла, Лариса проиграла; 2) Катя проиграла, Лариса проиграла.

Ответ: 1) совместные; 2) несовместные.

1. Ниже перечислены разные события. Укажите противоположные им события.

а) Мою новую соседку по парте зовут или Таня, или Аня.

б) Из пяти выстрелов в цель попали хотя бы два.

в) На контрольной я не решил, как минимум, три задачи из пяти.

Решение: а) Мою новую соседку по парте зовут не Таня и не Аня.

б) Из пяти выстрелов в цель попали менее двух.

в) На контрольной я решил максимум две задачи из пяти.

2. Назовите событие, для которого противоположным является такое событие:

а) на контрольной работе больше половины класса получили пятёрки;

б) все семь пулек в тире у меня попали мимо цели;

в) в нашем классе все умные и красивые;

г) в кошельке у меня есть три рубля одной монетой, или три доллара одной бумажкой.

Решение: а) «На контрольной работе пятёрки получили не более половины класса», или «на контрольной работе больше половины класса не получили пятёрки». б) «В тире хотя бы одна пулька из семи у меня попала в цель». в) «В нашем классе есть хотя бы один не умный или не красивый». г) «В кошельке у меня нет ни трёх рублей одной монетой, ни трёх долларов одной бумажкой».

1. Таня забыла последнюю цифру номера телефона знакомой девочки и набрала её наугад. Какова вероятность того, что Таня попала к своей знакомой?

Решение: На последнем месте в номере телефона может стоять одна из 10 цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; n=10; все предыдущие цифры никакого значения не имеют. Из n=10 только одна цифра верная, поэтому m=1. вероятность события А, состоящего в том, что, набрав последнюю цифру номера наугад, Таня попала к своей знакомой, равна =.

Ответ: .

2. Витя забыл две последние цифры номера телефона приятеля и набрал их наугад. С какой вероятностью этот звонок попадёт к приятелю?

Решение: Исходом в данном случае является пара десятичных цифр (0..9) с учётом порядка и с повторениями; общее число возможных исходов n=10×10=100; все исходы считаем равновозможными. Среди этих исходов только один является правильным, соответствующим номеру телефона приятеля. Таким образом, событию А – «звонок попадёт к приятелю» благоприятствует только один исход mA=1; вероятность =.

3. Для новогодней лотереи отпечатали 1500 билетов, из которых 120 выигрышных. Какова вероятность того, что купленный билет окажется выигрышным?

Решение: Если продажа билетов будет организована так, что покупка любого из 1500 билетов будет равновозможна, то можно применить формулу классической вероятности. Пусть событие А – «купленный билет оказался выигрышным». Тогда количество благоприятствующих исходов m=120, а общее число равновозможных исходов n=1500; вероятность

4. Для экзамена подготовили билеты с номерами от 1 до 25. какова вероятность того, что взятый наугад учеником билет имеет: 1) однозначный номер; 2) двузначный номер?

Решение: Общее число билетов n=25; извлечение каждого из них считается равновозможным. Рассмотрим событие А – «взятый билет имеет однозначный номер», В – «взятый билет имеет двузначный номер». Количество благоприятствующих исходов: mA=9 (одна цифра от 1 до 9); mB=16 (первая цифра 1 или 2, вторая цифра – от 0 до 9 после 1, от 0 до 5 после 2, всего 10+6=16). Искомые вероятности: ; =

Ответ: 1) ; 2) .

5. Ученик при подготовке к экзамену не успел выучить один из тех 25 билетов, которые будут предложены на экзамене. Какова вероятность того, что ученику достанется на экзамене выученный билет?

Решение: Общее число билетов n=25; выбор каждого билета равновозможен. Событие А – «ученику достанется на экзамене выученный билет»; количество благоприятствующих исходов m=25-1=24. Вероятность события А: ==0,96.

Ответ: .

6. В лотереи 1000 билетов, среди которых 20 выигрышных, приобретается один билет. Какова вероятность того, что этот билет: 1) выигрышный;

Решение: Общее число билетов n=1000; приобретение каждого из них равновозможно. Рассмотрим события и подсчитаем благоприятствующие им исходы: =, =.

7. Женя купил 2 лотерейных билета, и один из них оказался выигрышным. Можно ли утверждать, что вероятность выигрыша в лотереи ?

Ответ: Нет. Одного испытания не достаточно, чтобы по частоте узнать вероятность.

8. Алёша забыл последнюю цифру телефонного номера и набрал её наугад,

помня только, что эта цифра нечётная. Найти вероятность того, что номер

Решение: Исходом в данном случае являются цифры от 0 до 9, таких цифр – 10, но среди них нечётных только – 5. Отсюда следует, что M=5, N=10, значит

=.

9. В классе 20 мальчиков и 10 девочек.

а) На класс дали один билет в цирк, который решено разыграть по жребию. Какова вероятность, что в цирк пойдёт мальчик?

б) Учитель истории знает, что 3 девочки и 5 мальчиков из класса были накануне в кино, поэтому не выучили домашнее задание. К сожалению, он не знает их фамилий, но очень хочет поставить кому-нибудь двойку. Кого ему лучше вызвать к доске – мальчика или девочку?

в) Влад не решил домашнюю задачу по математике. Какова вероятность, что учитель этого не узнает, если за урок он успевает спросить пятерых?

Ответ: а) 0,067; б) лучше вызвать девочку; в) 0,833.

10. Для школьного новогоднего вечера напечатали 125 пронумерованных пригласительных билетов, между которыми предполагается разыграть главный приз. Какова вероятность, что номер счастливчика будет оканчиваться: а) на тройку; б) на девятку? в) Вова получил пригласительный билет с номером 33, а Таня – 99. Верно ли, что у Вовы больше шансов получить главный приз?

Ответ: а) 0,104; б) 0,096; в) Нет, не верно. У обоих шансы равны.

11. У Вики две одинаковые пары варежек. Уходя на улицу, она наугад берёт две варежки. Какова вероятность, что они окажутся парными (т. е. на разные руки)?

Ответ:

12. Вика потеряла одну из варежек на улице, и теперь их у неё три. Уходя на улицу, она по-прежнему выбирает две варежки случайным образом. Какова вероятность того, что они окажутся парными?

Ответ: .

13. В лотереи участвуют 100 билетов. Разыгрывается один приз. а) Какова вероятность того, что вы ничего не выиграете на свой единственный билет?

б) Участвуя в той же лотереи, вы купили 20 билетов. Какова вероятность, что вы опять останетесь ни с чем?

Решение: а) Общее число исходов равно 100. Благоприятных исходов – 1, значит =; б) Общее число исходов равно 100. Благоприятных исходов – 80, значит =.

1. Дано распределение дней рождения старшеклассников (учащихся 9-11 классов) по месяцам и дням недели

Источник