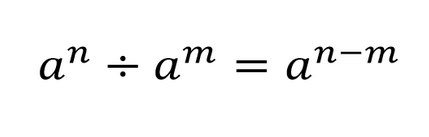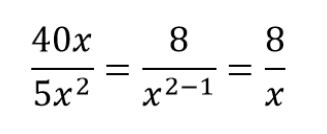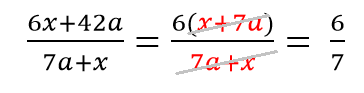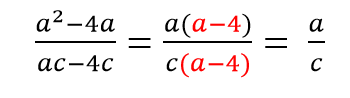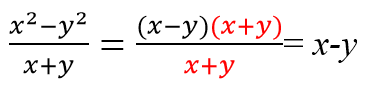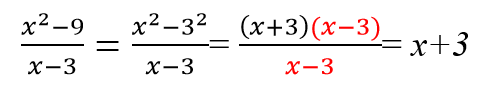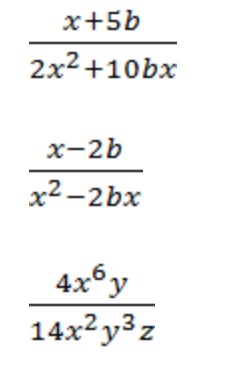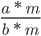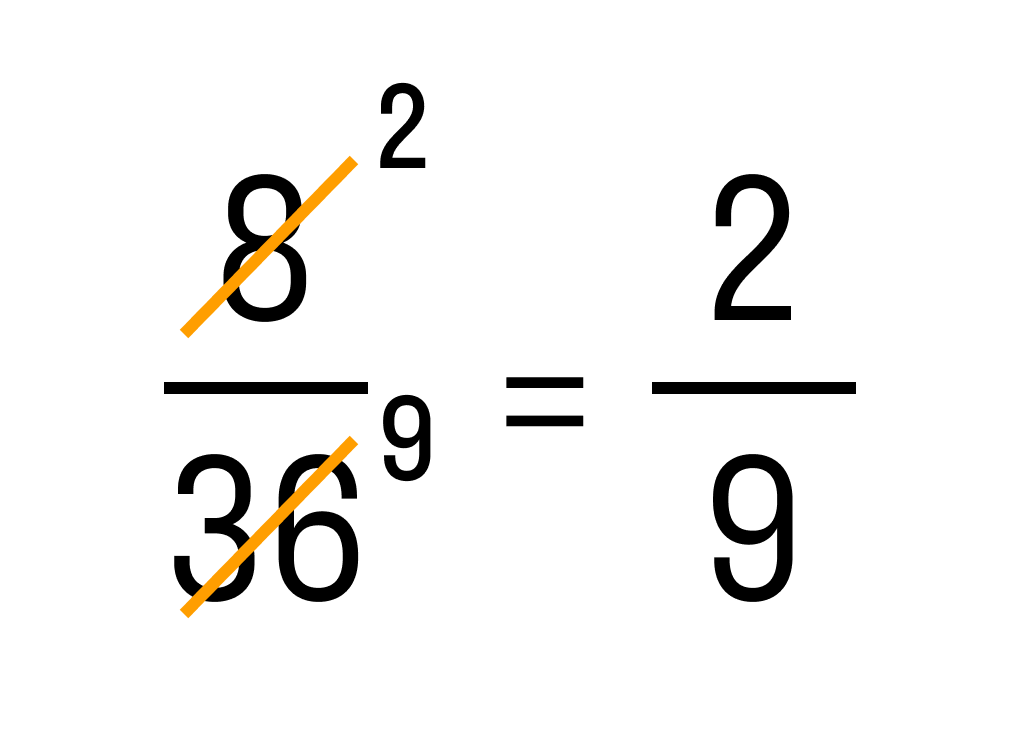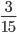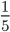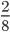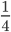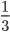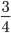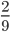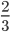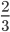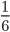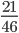в каком классе проходят сокращение дробей

Урок математики в 6-м классе на тему «Сокращение дробей»

Разделы: Математика

Ход урока

I. Устный счет: “МАТЕМАТИЧЕСКАЯ ЗАРЯДКА”.

Задание написано на доске, учащиеся должны определить, какое из равенств является верным, а какое нет. Учитель показывает физические упражнения, которые соответствуют ответу “да” и “нет”, а дети показывают то из них, которое означает, на их взгляд, правильный ответ.

ВЕРНО ЛИ РАВЕНСТВО:

а) ;
б) ;
в) ;
г) ;
д) ;
е) ;
ж) ;
з) ?

II. Игра: “КТО БЫСТРЕЕ СЯДЕТ В РАКЕТУ”.

а) На каком свойстве основано сокращение дробей?
б) Какая дробь называется несократимой?
в) Что меняется при сокращении дроби?

а) ;
б) ;
в) .

а) ;
б) ;
в) .

4. Найдите сумму дробей и сократите результат:

а) ;
б) ;
в) .

5. Сократите неправильную дробь, и затем выделите из нее целую часть:

а) ;
б) ;
в) .

6. Какую часть прямого угла составляет угол, равный:

7. Какую часть метра составляют

III. Закрепление.

На доске записаны выражения, а под ними ответы, но не по порядку. Ученики должны найти для каждого выражения правильный ответ. Несколько учеников работают на переносных досках, а все остальные на местах.

СОКРАТИТЕ ДРОБНОЕ ВЫРАЖЕНИЕ:

а) ;
б) ;
в) ;
г) ;
д) ;
е) ;

ОТВЕТЫ: 1,2; 0,1; 0,5; 1; 3; 0,5.

IV. Домашнее задание.

Учебник “Математика 6” стр.41 (ответить на вопросы 1 и 2), № 281, 282.

V. Самостоятельная работа.

Детям раздается дидактический материал.

1 вариант	2 вариант	3 вариант	4 вариант
а)	а)	а)	а)
б)	б)	б)	б)
в)	в)	в)	в)

2. СОКРАТИТЕ ДРОБНОЕ ВЫРАЖЕНИЕ:

1 вариант	2 вариант	3 вариант	4 вариант
а)	а)	а)	а)
б)	б)	б)	б)
в)	в)	в)	в)

Источник

Как сокращать алгебраические дроби?

Определение

Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:

Алгебраическая дробь содержит буквенные множители и степени.

Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.

Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.

Сокращение алгебраических дробей

Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.

Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.

Сокращение дробей с буквами и степенями проходит в три этапа:

Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:

Пример сокращения дроби со степенями и буквами:

Получаем сокращенную дробь.

Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.

❌ Так нельзя	✅ Так можно

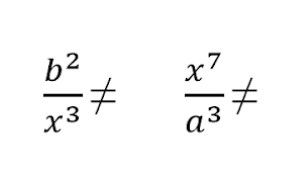Примеры сокращения алгебраических дробей с одночленами:

Пример сокращения №1.

Получаем сокращенную алгебраическую дробь.

Пример сокращения №2.

Получаем сокращенную дробь.

Сокращение алгебраических дробей с многочленами

Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:

Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.

Примеры сокращения алгебраических дробей с многочленами:

Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).

Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.

Вынесение общего множителя при сокращении дробей

При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.

Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:

Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.

Пример 1.

Пример 2.

Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.

Сокращение дробей. Формулы сокращенного умножения

Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.

Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.

Примеры сокращения дробей с помощью формул сокращенного умножения:

Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.

Примеры сокращения дробей за 7 и 8 классы

Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.

Источник

Конспекты урока математики в 5 классе по темпе «»Сокращение дробей»

Ищем педагогов в команду «Инфоурок»

1. Организационный момент. Приветствие. (1 мин)

Пусть девизом нашего сегодняшнего урока будет такой стишок:

Кто ничего не замечает

Тот ничего не изучает

Кто ничего не изучает,

Тот вечно хнычет и скучает

А нам с вами сегодня, надеюсь, скучать не придется.

2. Актуализация знаний. (5 мин)

Прежде, предлагаю немного размяться и вспомнить то, что мы изучали на предыдущих уроках.

На слайдах появляются картинки с вопросами.

1. Какая часть фигуры закрашена? (слайд 1)

2. В году 365 дней. Какую часть года составляют февраль в обычном и високосном году? (слайд 2)

3. Первоклассник спит 9 часов в сутки, а учится 5 часов. Какую часть суток он спит, а какую учится? (слайд 3)

4. Вставить пропущенные слова: (слайд 4)

Каждый может за версту

Видеть дробную черту

Над чертой ________ (числитель), знайте

Под чертою _________(знаменатель)

Дробь такую непременно

Надо звать ___________ (обыкновенной)

Знаменатель показывает (на сколько частей делим целое), а числитель (сколько частей целого взяли)

Молодцы! Справились с этим заданиями.

5. А теперь давайте вспомним, в чем заключается основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же число (отличное от 0), то получится дробь равная данной. (слайд 5)

Формулировка темы урока. (На слайде круг, разделенный на части) (3 мин)

А теперь следующее задание. Скажите, какая часть круга закрашена на первой картинке? (8/12) (слайд 6)

А на второй картинке? (4/6)

Глядя на эти рисунки, что мы можем сказать о дробях, выражающих закрашенную часть круга? (Они равны)

Т.е. можем записать, что . Так?

Взгляните теперь на третью картинку. Какая часть круга закрашена? (2/3) Что про эту дробь можем сказать? (Она тоже равна двум предыдущим)

Значит, можем записать:

(слайд 7)

А как получилась из дроби 8/12 дробь 4/6? (числитель и знаменатель делили на 2)

А из второй дроби третья?

Скажите, что мы делаем с дробью? (упрощаем, уменьшаем, сокращаем)

(По сравнению с первой дробью, что можно сказать о третьей)

Согласно основному свойству дроби (которое мы вспомнили перед началом урока) мы

можем делить числитель и знаменатель дроби на одно и то же число. И будет получаться

Преобразование, которое было выполнено, называется сокращением дроби.

Догадались о чем мы будем с вами говорить? Сформулируйте тему урока

Тема: Сокращение дробей» (слайд 8)

Запишите в тетради тему урока.

Сформулируйте цель урока. Что бы вы хотели узнать на этом уроке?

Эпиграфом к уроку пусть станут слова древнеримского оратора и философа Цицерона «Без знания дробей никто не может признаться знающим математику» (слайд 9)

3. Открытие новых знаний. (5 мин)

Что нужно сделать, чтобы сократить дробь?

Давайте откроем учебник (стр. 141) и посмотрим.

Работа с учебником.

Читаем вслух правило.

Сократить дробь — это значит, числитель и знаменатель дроби разделить на

одно и то же число, отличное от нуля. (слайд 10)

Пример. Возьмем дробь . Попробуем её сократить. Посмотрите, как это сделано в учебнике.

(Запишем пример в тетрадь)

Можно записывать по-другому (образец записи в учебнике на стр. 141 слева на полях)

А можно сократить еще дробь ? (Нет)

Дробь, которую нельзя сократить называется несократимой.

Другими нельзя подобрать такое число, на которое бы одновременно могли разделить числитель и знаменатель.

Оказывается, что некоторые дроби сократить нельзя.

Среди всех дробей равных , несократимая только одна.

Приведите еще примеры несократимых дробей.

При сокращении дробей:

Необходимо сокращать дробь до тех пор пока это возможно, т.е. пока не придем к несократимой дроби. (слайд 11)

Сокращение можно выполнять последовательно:

Пример: .

(Пример оформления в учебнике на стр. 141)

4. Первичное закрепление знаний

За доской два человека выполняют № 497 (по четыре примера каждый) (На выполнение номера дается 5 минут)

Потом вместе проверяем

Дополнительное задание для тех, кто сделал раньше № 498

5. Физкультминутка. (2 мин)

Раздаю на каждый ряд карточки. Каждый ученик вытягивает по одной. На карточке дробь. Дроби попарно равны. Тот, кто вытягивает равную дробь становится в соответствующую пару.

6. Введение нового знания в систему знаний. (5 мин)

Задание на слайде. Перетащите несократимые дроби в карман, а те которые можно сократить сократите (работа по вариантам со взаимопроверкой)

Первый вариант записывает те дроби, которые можно сократить и выполняет сокращение, а второй вариант записывает дроби, которые нельзя сократить.

(Тот, кому не досталось пары работает у доски, выписывая несократимые дроби)

Дроби: , , , , , , , .

Несократимые дроби: , , , , .

Сократимые дроби: , , .

После выполнения задания учащиеся обмениваются тетрадями и проверяют друг друга и ставят друг другу оценки.

Правильные ответы на слайде.

Работа в парах. При каких натуральных значениях букв получатся равные дроби: (4 мин)

а) ; б) ; в) ; г)

Историческая справка. На слайдах дроби в Древнем Египте, Риме, Вавилоне и на Руси.

А теперь, чтобы закрепить материал выполним задание посложней.

№ 502 из учебника. (6 мин)

8. Домашнее задание

Что нового узнали на уроке?

Что значит сократить дробь?

Всякую ли дробь можно сократить?

Как называют дробь, которую нельзя сократить?

Оцените свою деятельность на уроке…

— Мне всё удалось (поднимите руку)

— У меня остались вопросы (поднимите руку)

— Мне было интересно (сделайте один хлопок)

Источник

Сокращение обыкновенных дробей

Что такое «сокращение дробей»

Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.

Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.

В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:

Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.

С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:

=

=

где a, b, m — натуральные числа.

Графически сокращение дробей обычно записывается вот так:

Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.

Пример 1. Сократим обыкновенную дробь

Разделим числитель и знаменатель на общий делитель 3.

= =

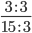
Сокращение выполнено: =

Пример 2. Сократим обыкновенную дробь

Разделим числитель и знаменатель на общий делитель 2.

= =

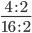
Сокращение выполнено: =

Приведение дробей к несократимому виду

Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.

Так, в результате сокращения в примере 2, мы из дроби получили дробь

Выходит, что дробь выдержит еще одно сокращение и придет к виду

Сокращая дробь, стремитесь в итоге получить несократимую дробь.

Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.

— несократимая дробь, так как по свойствам НОД мы знаем, что:

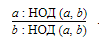
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.

Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.

Пример 3. Приведите обыкновенную дробь к несократимому виду

Найдем НОД числителя и знаменателя. НОД = 12

Найдем частное: 12 : 12 = 1

= =

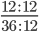
Сокращение выполнено: =

Пример 4. Приведите обыкновенную дробь к несократимому виду

Найдем НОД числителя и знаменателя. НОД = 5

Найдем частное: 15 : 5 = 3

= =

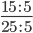
Сокращение выполнено: =

Правило сокращения дробей

Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.

Выполняйте сокращение дробей по следующему алгоритму:

В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.

Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.

Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7

Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.

Пример 5. Сократите дробь

Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5

Мысленно убираем все общие множители и перемножаем оставшиеся.

= =

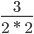
Сокращение выполнено: =

Пример 6. Сократите обыкновенную дробь

Найдем НОД числителя и знаменателя. НОД = 9

= =

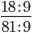
Сокращение выполнено: =

Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.

Пример 6. Сократите дробь:

= = =

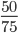
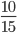
Сокращение выполнено: =

Пример 7. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

168 = 2 * 2 * 2 * 3 * 7

240 = 2 * 2 * 2 * 2 * 3 * 5

Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24

НОД 168 и 240 равен 24

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7

= =

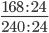
Сокращение выполнено: =

Пример 8. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

360 = 2 * 2 * 2 * 3 * 3 * 5

540 = 2 * 2 * 3 * 3 * 3 * 5

Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180

НОД 360 и 540 равен 180

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2

= =

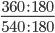
Сокращение выполнено: =

Пример 8. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

420 = 2 * 2 * 3 * 5 * 7

2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7

Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420

НОД 420 и 2520 равен 420

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1

= =

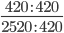
Сокращение выполнено. Дробь приведена к несократимому виду: =

Пример 9. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

1575 = 3 * 3 * 5 * 5 * 7

3450 = 2 * 3 * 5 * 5 * 23

Перемножаем все общие множители между собой 3 * 5 * 5 = 75

НОД 1575 и 3450 равен 72

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21

= =

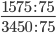
Сокращение выполнено. Дробь приведена к несократимому виду: =

Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.

Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.

Источник