Что такое уровень доверия в статистике

Уровень значимости и уровень надежности в EXCEL

history 23 ноября 2016 г.

Дадим определение терминам уровень надежности и уровень значимости. Покажем, как и где они используется в MS EXCEL .

СОВЕТ : Для понимания терминов Уровень значимости и Уровень надежности потребуется знание следующих понятий:

Уровень значимости обычно обозначают греческой буквой α ( альфа ). Чаще всего для уровня значимости используют значения 0,001; 0,01; 0,05; 0,10.

Уровень надежности

Термин Уровень надежности имеет синонимы: уровень доверия, коэффициент доверия, доверительный уровень и доверительная вероятность (англ. Confidence Level , Confidence Coefficient ).

В математической статистике обычно используют значения уровня доверия 90%; 95%; 99%, реже 99,9% и т.д.

Например, Уровень доверия 95% означает, что событие, вероятность которого 1-0,95=5% исследователь считать маловероятным или невозможным. Разумеется, выбор уровня доверия полностью зависит от исследователя. Так, степень доверия авиапассажира к надежности самолета, несомненно, должна быть выше степени доверия покупателя к надежности электрической лампочки.

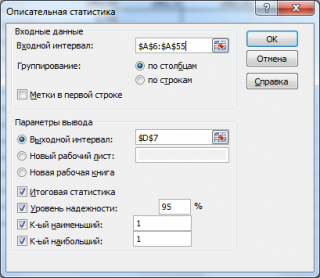
Уровень надежности в MS EXCEL

После нажатия кнопки ОК будет выведено другое диалоговое окно.

Если Уровень надежности задан 95%, то надстройка Пакет анализа использует следующую формулу (выводится не сама формула, а лишь ее результат):

или эквивалентную ей

где =СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка)) – является стандартной ошибкой среднего (формулы приведены в файле примера ).

=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95; СТАНДОТКЛОН.В(Выборка); СЧЁТ(Выборка))

Источник

Формула доверия

Сегодня мы расскажем об одной из ключевых фишек нашей DLP-системы — уровне доверия. Это показатель, который присваивается каждому человеку в компании и отражает вероятность того, что данный сотрудник окажется нарушителем.

Сейчас в DLP-решениях на первый план выходит аналитика. Пару лет назад все российские вендоры стали понемногу пытаться «разворачивать» DLP-системы от борьбы с утечками в сторону выявления и предотвращения других нелегитимных действий сотрудников — мошенничества, откатов, сговоров и т.п. Однако каждый человек генерирует такое количество информации в день, что отслеживать действия каждого невозможно даже в средних компаниях, не говоря о крупном бизнесе. Поэтому способность системы сделать качественную аналитику в автоматическом режиме и очертить круг лиц «под подозрением» была бы очевидным преимуществом. Так возникла идея создания уровня доверия, основной целью которого была прозрачность ситуации с внутренними угрозами в компании.

Мы хотели, чтобы безопасник мог быстро, без долгого анализа данных DLP-системы, понять, к кому в компании стоит присмотреться повнимательнее. Очень простая и изящная концепция, не так ли? Казалось бы, идея лежит на поверхности. Однако чтобы создать такую формулу доверия, которая не вызывала бы бешеного количества ложных срабатываний, потребовалось проделать серьезную работу и связать в одно целое результаты социальной инженерии, статистики и бизнес-анализа. В этой статье мы расскажем о том, как вывести формальное выражение величины доверия к сотрудникам с точки зрения защиты от умышленной или случайной утечки. Судя по реальной статистике совершающихся инцидентов, формула эта оказалась достаточно точной.

Немного теории

Идея автоматического профилирования персон в системах DLP не просто витает в воздухе, но и часто фигурирует в международных стандартах и рекомендациях по безопасности. А вот ее реализация на сегодняшний день не имеет общепринятой методологии. Естественным путем является построение такого показателя на основе анализа большого объема данных (Big Data). На языке Big Data техники эта проблема относится к управлению репутацией и доверием («Trust and reputation management» [1]).

По своей природе профилирование относится к области поведенческого анализа. С точки зрения бизнес-поведения здесь применяются методы современной психологии, физиологии, социологии [2, 3].

В качестве вычислительного аппарата рассматриваются методы математической статистики, случайных процессов, статистической физики 4. Отдельная ветвь моделей опирается на теорию нейронных сетей [10, 11].

Формула доверия — точность и простота

Консультации с экспертами в области защиты информации от утечки позволили выделить среди теоретических методов наиболее эффективные: социология, математическая статистика, бизнес-анализ. Даже такой набор методов очень обширен, и их верификация весьма трудоемка, несмотря на то, что комбинировать эти методы — занятие увлекательное. Поэтому мы начали с отбора наиболее подходящих для нашей цели методик. Основными критериями при выборе были точность и простота.

Мы решили, что лучшим показателем точности служит то, сколько человек из числа реальных злоумышленников, обнаруженных офицерами безопасности, система смогла автоматически определить в качестве потенциальных нарушителей. Таким образом, мы сравнивали результаты работы офицера безопасности и расчеты разных методик.

Второй критерий — простота — отвечает за то, чтобы в модели уровня доверия отсутствовали избыточные переменные (факторы). Дело в том, что каждый дополнительный фактор вносит неопределенность, вследствие этого теряется прозрачность результата. Иными словами, если уровень доверия, присвоенный человеку, резко изменится, безопаснику будет труднее понять, чем вызваны эти изменения. Это бы свело на нет наши усилия по достижению главной цели — сделать данные DLP-аналитики максимально наглядными и прозрачными для пользователя.

Согласно этим критериям был принят оптимальный алгоритм, заложенный впоследствии в DLP-систему.

Исходные данные

Мы располагаем очень обширным массивом данных по реальным инцидентам безопасности. В ходе каждого внедрения и пилотного проекта создаются отчеты по событиям и инцидентам. Эти отчеты также содержат информацию о нарушителях — кадровые сведения, список событий, связанных с этим сотрудником, признаки для занесения человека в группу повышенного риска.

В качестве реальных данных выступали данные инцидентов по 8-ми отраслям:

«С» №1 — Статистика

В качестве статистического инструмента мы выбрали традиционную модель авторегрессии с ошибкой в виде белого шума. Такая модель позволяет подобрать лучшую линию (закон) на графике зависимости учитываемых факторов. Эта модель показала хороший результат на ряде подобных задач.

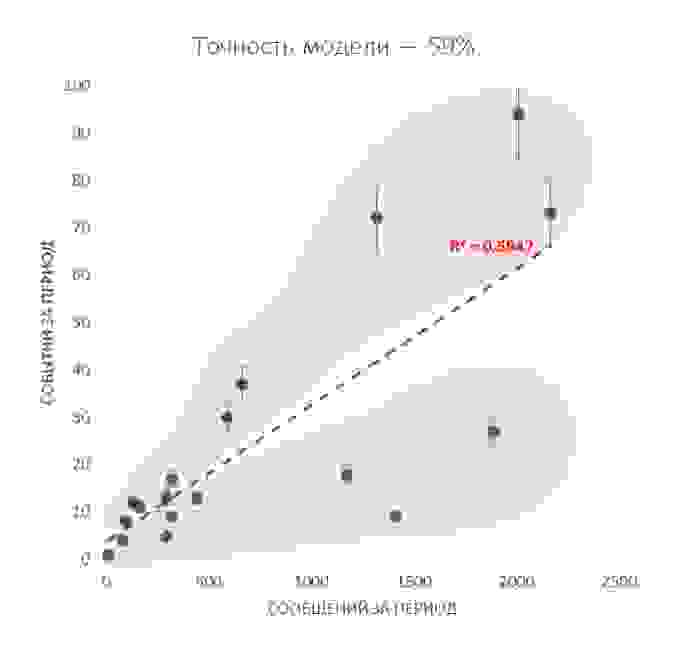
Факторный анализ мы начали со сравнения объема переписки персоны и числа событий, обнаруженных в этой переписке. Полагая, что события линейно зависят от объема переписки, мы получим такой закон зависимости событий от числа сообщений:

График функции зависимости обозначен пунктиром по причине того, что в некотором смысле «точность» этого закона (величина R 2 ) недостаточна, чтобы считать этот закон сколь-нибудь приемлемым для всех персон. Обычно для критериев точности мы принимаем нижний порог этой величины в 0,8.

Следующим шагом, который позволяет сделать статистика, стало «слепое» разделение персон по группам. Разделение дихотомическое — делим все персоны на 2 группы, и, если точность модели становится достаточной, принимаем такое разбиение. В противном случае, делим каждую подгруппу еще на 2 и так далее. На практике достаточно 1-2 итераций.

Статистическое деление на группы персон уже на первой итерации дало убедительную «точность» — более 90%. Естественно, отдельно решается вопрос достаточности объема выборки для такого вывода.

При достаточно хорошей выборке, линия регрессии (закон зависимости) может применяться как прогноз для любой персоны. И отклонения персон от этого закона можно с точки зрения статистики относить к аномалиям.

Все бы хорошо, но статистика, не подкрепленная бизнес-смыслом, зачастую дает неадекватные реальному положению дел результаты.

«С» №2 — Социология

На третьем этапе мы несколько скорректировали нашу модель. Нам необходимо было понять, что связывает персон внутри каждой статистически выделенной группы. Поэтому возникла необходимость поиска особенностей, согласующихся со статистическим разбиением. Для этого мы воспользовались методами социологии и бизнес-анализа.

Мониторинг социологических исследований и практическая их оценка дали такие варианты категорий персон:

Продвинутые пользователи хорошо знакомы с IT-инфраструктурой и особенно продвинуты в модификации, подмене данных. Для этой группы требуется особый контроль рабочих станций и используемых программ на уровне ядра ОС. Интерес представляют также коммуникации продвинутых пользователей и халатных пользователей, так как первые могут воспользоваться недостаточной ИБ-компетентностью вторых. В группе продвинутых пользователей распространены инциденты, связанные с кибербезопасностью, лавинные события, события, связанные с корпоративными системами документооборота и базами данных.

«С» №3 — Специфика бизнеса

Касаясь бизнес-факторов, особенно важно определить степень детализации, чтобы избежать неэффективного усложнения модели.

Конечно, в идеальном случае у офицера безопасности имеются схемы бизнес-процессов, в которые вовлечены коммерчески важные данные. В реальности такое встречается крайне редко.
В этих ситуациях выручает возможность систем DLP определять в информационном потоке виды документов и визуализировать их перемещение. При этом даже на небольшом периоде наблюдения накопленные сведения дают наглядную картину того, как в рамках тех или иных процессов перемещаются данные. Мы выделили несколько групп сотрудников, в их числе:

Особым положением пользуется группа материально ответственных сотрудников. Для них характерно преобладание событий, связанных с экономическими событиями безопасности. В сфере учета обычно используется некоторый отраслевой workflow, который можно успешно учитывать правилами политик автоматизированной системы DLP.

Итоговая формула уровня доверия

В ходе оценки различных моделей уровня доверия стало ясно, что он должен зависеть от:

С помощью модели, учитывающей эти факторы, мы смогли автоматически определить более 60% от общего числа нарушителей, независимо выявленных офицерами безопасности в ходе расследований и разборов инцидентов.

Такой результат стал весомым аргументом для того, чтобы на практике реализовать в DLP-решении динамический уровень доверия.

Заключение

Несмотря на то, что сейчас уровень доверия успешно работает и является одним из ключевых элементов аналитики в нашей DLP-системе, мы постоянно работаем над усовершенствованием формулы. Возможно, когда-нибудь в будущем сможем написать продолжение этой статьи под названием «Как мы сделали формулу доверия точнее в несколько раз».

Вероятнее всего, в развитии технологии поможет и конкуренция. Пока мы одни из DLP-вендоров всерьез играем на этом поле, однако, как уже говорилось в начале статьи, поведенческий анализ сейчас в тренде, так что наверняка скоро в эту сторону массово начнут смотреть и другие отечественные разработчики.

Источник

Доверительные интервалы

Определение

Доверительные интервалы (англ. Confidence Intervals) одним из типов интервальных оценок используемых в статистике, которые рассчитываются для заданного уровня значимости. Они позволяют сделать утверждение, что истинное значение неизвестного статистического параметра генеральной совокупности находится в полученном диапазоне значений с вероятностью, которая задана выбранным уровнем статистической значимости.

Нормальное распределение

Когда известна вариация (σ 2 ) генеральной совокупности данных, для расчета доверительных пределов (граничных точек доверительного интервала) может быть использована z-оценка. По сравнению с применением t-распределения, использование z-оценки позволит построить не только более узкий доверительный интервал, но и получить более надежные оценки математического ожидания и среднеквадратического (стандартного) отклонения (σ), поскольку Z-оценка основывается на нормальном распределении.

Формула

Для определения граничных точек доверительного интервала, при условии что известно среднеквадратическое отклонение генеральной совокупности данных, используется следующая формула

где X – математическое ожидание выборки, α – уровень статистической значимости, Z_α/2 – Z-оценка для уровня статистической значимости α/2, σ – среднеквадратическое отклонение генеральной совокупности, n – количество наблюдений в выборке. При этом, σ/√ n является стандартной ошибкой.

Таким образом, доверительный интервал для уровня статистической значимости α можно записать в виде

Пример

Предположим, что размер выборки насчитывает 25 наблюдений, математическое ожидание выборки равняется 15, а среднеквадратическое отклонение генеральной совокупности составляет 8. Для уровня значимости α=5% Z-оценка равна Z_α/2=1,96. В этом случае нижняя и верхняя граница доверительного интервала составят

А сам доверительный интервал может быть записан в виде

Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности попадет в диапазон от 11,864 до 18,136.

Методы сужения доверительного интервала

Допустим, что диапазон [11,864; 18,136] является слишком широким для целей нашего исследования. Уменьшить диапазон доверительного интервала можно двумя способами.

Снизив уровень статистической значимости до α=10%, мы получим Z-оценку равную Z_α/2=1,64. В этом случае нижняя и верхняя граница интервала составят

А сам доверительный интервал может быть записан в виде

В этом случае, мы можем сделать предположение, что с вероятностью 90% математическое ожидание генеральной совокупности попадет в диапазон [12,376; 17,624].

Если мы хотим не снижать уровень статистической значимости α, то единственной альтернативой остается увеличение объема выборки. Увеличив ее до 144 наблюдений, получим следующие значения доверительных пределов

Сам доверительный интервал станет иметь следующий вид

Таким образом, сужение доверительного интервала без снижения уровня статистической значимости возможно только лишь за счет увеличения объема выборки. Если увеличение объема выборки не представляется возможным, то сужение доверительного интервала может достигаться исключительно за счет снижения уровня статистической значимости.

Построение доверительного интервала при распределении отличном от нормального

В случае если среднеквадратичное отклонение генеральной совокупности не известно или распределение отлично от нормального, для построения доверительного интервала используется t-распределение. Это методика является более консервативной, что выражается в более широких доверительных интервалах, по сравнению с методикой, базирующейся на Z-оценке.

Формула

Для расчета нижнего и верхнего предела доверительного интервала на основании t-распределения применяются следующие формулы

где X – математическое ожидание выборки, α – уровень статистической значимости, t_α – t-критерий Стьюдента для уровня статистической значимости α и количества степеней свободы (n-1), σ – среднеквадратическое отклонение выборки, n – количество наблюдений в выборке.

Сам доверительный интервал может быть записан в следующем виде

Распределение Стьюдента или t-распределение зависит только от одного параметра – количества степеней свободы, которое равно количеству индивидуальных значений признака (количество наблюдений в выборке). Значение t-критерия Стьюдента для заданного количества степеней свободы (n) и уровня статистической значимости α можно узнать из справочных таблиц.

Пример

Предположим, что размер выборки составляет 25 индивидуальных значений, математическое ожидание выборки равно 50, а среднеквадратическое отклонение выборки равно 28. Необходимо построить доверительный интервал для уровня статистической значимости α=5%.

В нашем случае количество степеней свободы равно 24 (25-1), следовательно соответствующее табличное значение t-критерия Стьюдента для уровня статистической значимости α=5% составляет 2,064. Следовательно, нижняя и верхняя граница доверительного интервала составят

А сам интервал может быть записан в виде

Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [38,442; 61,558].

Использование t-распределения позволяет сузить доверительный интервал либо за счет снижения статистической значимости, либо за счет увеличения размера выборки.

Снизив статистическую значимость с 95% до 90% в условиях нашего примера мы получим соответствующее табличное значение t-критерия Стьюдента 1,711.

В этом случае мы можем утверждать, что с вероятностью 90% математическое ожидание генеральной совокупности окажется в диапазоне [40,418; 59,582].

Если мы не хотим снижать статистическую значимость, то единственной альтернативой будет увеличение объема выборки. Допустим, что он составляет 64 индивидуальных наблюдения, а не 25 как в первоначальном условии примера. Табличное значение t-критерия Стьюдента для 63 степеней свободы (64-1) и уровня статистической значимости α=5% составляет 1,998.

Это дает нам возможность утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [43,007; 56,993].

Выборки большого объема

К выборкам большого объема относятся выборки из генеральной совокупности данных, количество индивидуальных наблюдений в которых превышает 100. Статистические исследования показали, что выборки большего объема имеют тенденцию быть нормально распределенными, даже если распределение генеральной совокупности отличается от нормального. Кроме того, для таких выборок применение z-оценки и t-распределения дают примерно одинаковые результаты при построении доверительных интервалов. Таким образом, для выборок большого объема допускается применение z-оценки для нормального распределения вместо t-распределения.

Подведем итоги

В таблице собраны рекомендации по выбору методики построения доверительных интервалов для различных ситуаций.

Источник

Доверительные интервалы

Общий обзор

Взяв выборку из популяции, мы получим точечную оценку интересующего нас параметра и вычислим стандартную ошибку для того, чтобы указать точность оценки.

Однако, для большинства случаев стандартная ошибка как такова не приемлема. Гораздо полезнее объединить эту меру точности с интервальной оценкой для параметра популяции.

Это можно сделать, используя знания о теоретическом распределении вероятности выборочной статистики (параметра) для того, чтобы вычислить доверительный интервал (CI – Confidence Interval, ДИ – Доверительный интервал) для параметра.

Вообще, доверительный интервал расширяет оценки в обе стороны некоторой величиной, кратной стандартной ошибке (данного параметра); два значения (доверительные границы), определяющие интервал, обычно отделяют запятой и заключают в скобки.

Доверительный интервал для среднего

Использование нормального распределения

Выборочное среднее имеет нормальное распределение, если объем выборки большой, поэтому можно применить знания о нормальном распределении при рассмотрении выборочного среднего.

В частности, 95% распределения выборочных средних находится в пределах 1,96 стандартных отклонений (SD) среднего популяции.

Когда у нас есть только одна выборка, мы называем это стандартной ошибкой среднего (SEM) и вычисляем 95% доверительного интервала для среднего следующим образом:

Если повторить этот эксперимент несколько раз, то интервал будет содержать истинное среднее популяции в 95% случаев.

Обычно это доверительный интервал как, например, интервал значений, в пределах которого с доверительной вероятностью 95% находится истинное среднее популяции (генеральное среднее).

Хотя это не вполне строго (среднее в популяции есть фиксированное значение и поэтому не может иметь вероятность, отнесённую к нему) таким образом интерпретировать доверительный интервал, но концептуально это удобнее для понимания.

Использование t-распределения

Можно использовать нормальное распределение, если знать значение дисперсии в популяции. Кроме того, когда объем выборки небольшой, выборочное среднее отвечает нормальному распределению, если данные, лежащие в основе популяции, распределены нормально.

Если данные, лежащие в основе популяции, распределены ненормально и/или неизвестна генеральная дисперсия (дисперсия в популяции), выборочное среднее подчиняется t-распределению Стьюдента.

Вычисляем 95% доверительный интервал для генерального среднего в популяции следующим образом:

где — процентная точка (процентиль) t-распределения Стьюдента с (n-1) степенями свободы, которая даёт двухстороннюю вероятность 0,05.

Вообще, она обеспечивает более широкий интервал, чем при использовании нормального распределения, поскольку учитывает дополнительную неопределенность, которую вводят, оценивая стандартное отклонение популяции и/или из-за небольшого объёма выборки.

Когда объём выборки большой (порядка 100 и более), разница между двумя распределениями (t-Стьюдента и нормальным) незначительна. Тем не менее всегда используют t-распределение при вычислении доверительных интервалов, даже если объем выборки большой.

Обычно указывают 95% ДИ. Можно вычислить другие доверительные интервалы, например 99% ДИ для среднего.

Вместо произведения стандартной ошибки и табличного значения t-распределения, которое соответствует двусторонней вероятности 0,05, умножают её (стандартную ошибку) на значение, которое соответствует двусторонней вероятности 0,01. Это более широкий доверительный интервал, чем в случае 95%, поскольку он отражает увеличенное доверие к тому, что интервал действительно включает среднее популяции.

Доверительный интервал для пропорции

Выборочное распределение пропорций имеет биномиальное распределение. Однако если объём выборки n разумно большой, тогда выборочное распределение пропорции приблизительно нормально со средним .

Оцениваем выборочным отношением p=r/n (где r– количество индивидуумов в выборке с интересующими нас характерными особенностями), и стандартная ошибка оценивается:

95% доверительный интервал для пропорции оценивается:

Если объём выборки небольшой (обычно когда np или n(1-p) меньше 5), тогда необходимо использовать биномиальное распределение для того, чтобы вычислить точные доверительные интервалы.

Заметьте, что если p выражается в процентах, то (1-p) заменяют на (100-p).

Интерпретация доверительных интервалов

При интерпретации доверительного интервала нас интересуют следующие вопросы:

Насколько широк доверительный интервал?

Широкий доверительный интервал указывает на то, что оценка неточна; узкий указывает на точную оценку.

Ширина доверительного интервала зависит от размера стандартной ошибки, которая, в свою очередь, зависит от объёма выборки и при рассмотрении числовой переменной от изменчивости данных дают более широкие доверительные интервалы, чем исследования многочисленного набора данных немногих переменных.

Включает ли ДИ какие-либо значения, представляющие особенный интерес?

Можно проверить, ложится ли вероятное значение для параметра популяции в пределы доверительного интервала. Если да, то результаты согласуются с этим вероятным значением. Если нет, тогда маловероятно (для 95% доверительного интервала шанс почти 5%), что параметр имеет это значение.

Источник