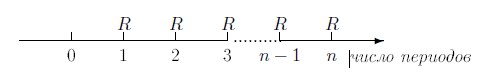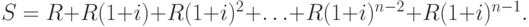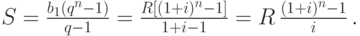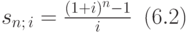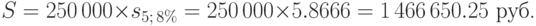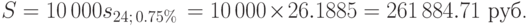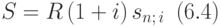что такое рента пренумерандо

Финансовые ренты

6.1 Основные определения

Финансовой рентой называется последовательность платежей, равных по величине и производящихся через равные промежутки времени.

Временной интервал между последовательными выплатами называется периодом ренты. Чаще всего встречаются ренты, период которых равен году, половине года, кварталу или месяцу. Срок от начала первого до конца последнего периода называется сроком ренты. Если последний период не указывается ( срок ренты бесконечный), то рента называется бессрочной.

Если выплаты производятся в конце периода, то рента называется обычной или постнумерандо, если выплаты производятся в начале периода, то рента называется авансированной или пренумерандо.

6.2 Функция коэффициентов для финансовой ренты

Сумма 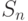первых n членов геометрической прогрессии, у которой , вычисляется по формуле:

Следовательно, наращенная сумма всей ренты в момент n будет равна:

Для коэффициента, на который умножается R в получившейся формуле, принято использовать следующее обозначение:

Тогда наращенная сумма финансовой ренты выражается формулой:

Из формулы (6.3) видно, что значение функции — это наращенная за n периодов сумма финансовой ренты с платежами, равными 1. Ранее, когда компьютеры еще не были так распространены, для выполнения расчётов по формуле (использовались специальные таблицы значений функции . Теперь для вычисления значений этой функции можно использовать финансовый калькулятор или программу Excel. Заметим, что функция не входит в число встроенных финансовых функций Excel. Но это легко исправить, так как нетрудно написать свою функцию, выполняющую вычисления по формуле (46), на VBA.

Рассмотрим два примера на применение формулы (6.3).

Пример 54. Фирма создаёт фонд помощи ветеранам труда, вкладывая ежегодно 250 000 руб. в банк, выплачивающий 8% годовых (сложных). Какая сумма будет на счёте фонда через 5 лет?

Пример 55. Предприниматель вкладывает 10 000 руб. в конце каждого месяца в банк, выплачивающий проценты по ставке 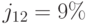. Какую сумму он накопит за 2 года?

Сделаем важное замечание, касающееся авансированных рент, когда платежи делаются в начале периода. Наращенная сумма авансированной ренты выражается формулой:

Действительно, вместе с авансированной рентой можно рассмотреть обычную ренту с тем же множеством платежей, которая начинается на один период раньше. Наращенные суммы этих рент в момент n должны совпадать, поэтому получаем формулу (6.4). Подобные несложные изменения потребуется выполнять и в остальных формулах, приведенных в этой лекции, если применять их для авансированных рент.

Источник

Различные виды постоянных рент

Различные виды постоянных рент

Далее рассматриваются ренты, которые отличаются от рассмотренных выше по применяемым процентным ставкам, срокам платежей, способу начисления процентов, моментом производства платежей.

Рента с простыми процентами. Современную величину А и наращенную сумму р-срочной продолжительностью n лет с годовой ставкой простых процентов i и годовым членом R определяют по формулам

Смешанные ренты. Срочные ренты (p > 1), у которых на платежи в пределах года начисляют простые проценты, а за годовые периоды − сложные, называют смешанными рентами. Современную величину Асм. и наращенную сумму Sсм. таких рент определяют по формулам

где R − годовой член ренты, − коэффициенты приведения и наращения обычных годовых рент (p = m = 1), i − годовая ставка процентов.

Рента с периодом, превышающим год. Пусть период ренты r > 1, проценты начисляются раз в конце года по ставке i годовых, платеж в конце периода равен Rr, срок ренты n кратен r. Тогда наращенная сумма S и современная величина А равны:

Вечная рента. Рента, число выплат которой бесконечно, называется вечной рентой. Современная величина А∞ вечной p-срочной ренты, с m-разовым начислением процентов в году по номинальной ставке j с годовым членом R

Отложенная рента. Начало действия отложенной, или отсроченной, ренты начинается спустя t лет после подписания финансового контракта. Очевидно, что запаздывание на t лет в выплате платежей по сравнению с обычной рентой не влияет на величину наращенной суммы отложенной (отсроченной) ренты. По иному обстоит дело с современной величиной отложенной ренты: она равна дисконтированному значению современной величины немедленной ренты (период дисконтирования равен величине t

отсрочки платежей). Дисконтный множитель должен соответствовать применяемым процентным ставкам и способу начисления процентов. Так, например, наращенная сумма St и современная величина Аt отложенной p-срочной ренты постнумерандо с

m-разовым начислением процентов в году равны:

где S и A ̶ наращенная сумма и современная величина соответствующей немедленной ренты постнумерандо.

Рента пренумерандо. Ренты с выплатами в начале периода называются рентами пренумерандо. При вычислении наращенной суммы и современной величины ренты пренумерандо можно использовать следующий прием. Все выплаты путем наращения вывести на конец соответствующих периодов и к вновь полученной ренте постнумерандо применить обычные формулы для вычисления наращенной суммы и современной величины ренты.

Так, например, наращенная сумма и современная величина p-срочной пренумерандо, с m-разовым начислением процентов в году равны:

где S и A ̶ наращенная сумма и современная величина соответствующей ренты постнумерандо.

Из этих формул следует, что наращенная сумма и современная величина рент пренумерандо больше соответствующих величин рент постнумерандо.

Ренты с платежами в середине периодов. Если поступления от произведенных инвестиций распределяются более или менее равномерно на протяжении периода, используют ренты с выплатами в середине периодов. В подобных ситуациях для уменьшения погрешности используют ренты с выплатами в середине периодов. В подобных ситуациях для уменьшения погрешности вычислений рекомендуется суммы поступлений за период относить к середине этого периода.

Наращенная сумма S1/2 и современная величина A1/2 p-срочной ренты с

m-разовым начислением процентов в году равны:

где S и A ̶ наращенная сумма и современная величина p-срочной ренты постнумерандо с m-разовым начислением процентов в году.

Ренты со случайными параметрами. В ряде случаев, когда один или несколько параметров ренты заранее не известны, их можно рассматривать как случайные величины с заданным или прогнозируемым законом распределения. Наращенная сумма и современная величина ренты в этом случае будут также случайными величинами. В таком случае естественно вести речь о вычислении среднего значения и дисперсии наращенной суммы или современной величины ренты. Если эти значения не удается вычислить аналитически, их можно оценить, моделируя значения соответствующих случайных величин.

Задачи аудиторной работы

1. Определить размеры постоянных взносов в начале каждого квартала, которые позволят накопить 1000 у. е. на счете банка с начислением по 1% ежемесячно в течение 10 лет.

2. Строительной фирмой заключен контракт на строительство здания. Согласно контракту, заказчик через 2 года после окончания строительства производит оплату в течение 3-х лет равными годовыми платежами, производимыми в конце года, в размере 2,5 млн. руб. каждый. Процентная ставка установлена в 10% годовых; проценты начисляются в конце года. Определить выигрыш заказчика, полученный в результате отсрочки платежей на 2 года.

/ Ответ. 1,079027 млн. руб. /

3. Участок сельскохозяйственных угодий может приносить ежегодный доход в

5. Определить постоянные взносы в конце каждого месяца на спецсчет банка, которые позволят за 30 лет накопить сумму, необходимую для того, чтобы в течение следующих 20 лет получать дополнительно к пенсии 150 у. е. в начале каждого месяца. Банк предлагает номинальную ставку 6% годовых с ежемесячным начислением процентов. Определить срок выплаты дополнительной пенсии, увеличенной в два раза. При необходимости скорректировать последнюю выплату.

/ Ответ. 20,95 у. е.; 7,171 лет; 314,59 у. е. /

Задачи для самостоятельного решения

1. На банковском счете накапливается 1000 у. е. с помощью постоянных взносов в начале каждого квартала по 25 у. е. На поступившие взносы начисляется ежемесячно 1%. Найти срок накоплений с целым количеством кварталов. Ри необходимости выполнить коррекцию всех взносов.

/ Ответ. 6,51; 25,07 у. е. /

2. Сравниваются два варианта строительства некоторого объекта. Первый требует разовых вложений в сумме 6 млн. руб. и капитального ремонта стоимостью

0,8 млн. руб. каждые 5 лет. Для второго затраты на создание 7 млн. руб., на капитальный ремонт – 0,4 млн. руб. каждые 10 лет. Временной горизонт, учитываемый в расчете – 50 лет. Процентная ставка – 10% годовых. Какой из вариантов является более выгодным?

/ Ответ. Второй вариант более выгоден /

/ Ответ. 88,322038 млн. /

Источник

Финансовые ренты (постнумерандо и пренумерандо)

Последовательность денежных поступлений, осуществляемых равными суммами через равные периоды (промежутки) времени, называют постоянной финансовой рентой.

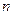
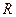
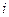
Пусть в течение —лет на счет вносится одна и та же сумма — член ренты. На взносы также в конце каждого года начисляются сложные проценты по ставке —% годовых. Наращенная сумма рентных платежей в этом случае определится по формуле:

(1.21.) (1.22.)

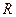
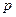
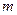
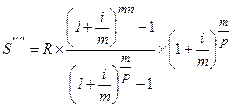
Если взносы в размере будут вноситься —раз в году (в конце или начале расчётных периодов) и на суммы на счёте — раз в году будут начисляться сложные проценты по годовой ставке , то наращенная сумма взносов за —лет в этом случае определится по формуле:

(1.23.) (1.24.)

Из приведенных формул путем несложных математических преобразований можно вывести формулы для определения размера взносов, обеспечивающих накопление заданной суммы . Например:

(1.25.)

Задача 1.4. На депозитный счет ежемесячно в конце месяца в течение 5 лет будут вносить по 500 руб. На сумму счета также в конце каждого месяца будут начисляться сложные проценты по ставке 22% годовых. Определить сумму, которую получит вкладчик при закрытии счета.

Наращенная сумма ренты постнумерандо в общем виде определяется по формуле:

(1.22.) = 53847 (тыс. руб)

Ответ: 53847 тыс. руб

Задача 1.5. Взносы в накопительный пенсионный фонд будут производиться в начале каждого месяца и на них ежеквартально будут начисляться сложные проценты по ставке 36% годовых. Определить размер взноса, если за 40 лет в фонде должна быть накоплена сумма 1 млн. руб.

Оценка эффективности финансовых операций

Показателем, выступающем в качестве меры эффективности вложений средств при различных условиях, является эквивалентная (эффективная) годовая ставка простых или сложных процентов ( ).

(1.26.) (1.27.)

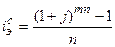
Задача 1.6.Финансовая компания в своем рекламном объявлении указывает, что вложенная сумма увеличивается на 0,46% ежедневно с начислением процентов на проценты. Определить эффективную годовую ставку процентов при заключении договора с компанией на 3 месяца.

(1.27.) = 2,05 или 205%

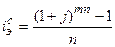
Расчеты в условиях инфляции

Инфляция характеризуется обесцениванием национальной валюты и общим повышением уровня цен.

Уровень инфляции 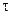(в %) показывает, на сколько процентов выросли цены за рассматриваемый период времени:

% (1.28.)

где — сумма, на которую надо увеличить первоначальную сумму для сохранения её покупательной способности в будущем.

— индекс инфляции (показывает во сколько раз выросли цены);

(1.29.) (1.30.)

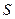
Индекс инфляции за период, состоящий из -го к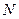оличества более коротких периодов, характеризующихся своим уровнем инфляции, можно определить по формуле:

(1.31.)

где — общее количество интервалов в наблюдаемом периоде.

При равных интервалах и равных уровнях инфляции за каждый интервал формула принимает вид:

(1.32.)

Будущую сумму ,характеризующую реальное, обесцененное в результате инфляции значение суммы , можно определить по формуле:

(1.33.)

Чтобы в условиях инфляции реальная покупательная способность будущих и современных сумм не отличалась, необходимо компенсировать потери от инфляции путем корректировки процентной ставки:

1. Точная корректировка осуществляется по формуле:

(1.34.)

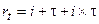
где — ставка брутто – ставка, учитывающая инфляцию;

— ставка процентов, характеризующая доходность операции без учета действия инфляции;

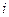
2. Приближённая корректировка:

(1.35.)

Вычисленное значение ставки брутто или следует подставлять в расчетные формулы вместо ставки процентов .

Задача 1.7.Определить ожидаемый годовой уровень инфляции при оптимистическом прогнозе ее величины за месяц на уровне 1,5%.

На основе месячного уровня инфляции определим индекс инфляции за год:

(1.32.) I_u = (1 + 0,015) 12 = 1,196 или 119,6%

Уровень инфляции определим по формуле:

(1.30.)

Ответ: уровень инфляции за год при оптимистическом прогнозе составит 19,6 %

С целью страхования потерь, вызванных действием инфляции, необходимо откорректировать ставку процентов, используемую для определения наращенной суммы долга. Точная корректировка осуществляется по формуле:

(1.34.)

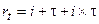
r_t = 0,05 + 0,06 + 0,05 * 0,06 = 0,113 или 11,3%

Вычисленную ставку процента подставляем в формулу для определения наращенной суммы долга вместо i

S c = 10000 * (1 + 0,113) 10 = 29171($)

Кредитные операции

Широко известны следующие способы погашения кредита (займа, долга):

· единовременным платежом в конце срока;

· единовременным платежом в конце срока путём создания погасительного фонда;

· равными срочными уплатами;

· частичными платежами актуарным методом;

· частичными платежами по правилу торговца.

При этом в расчетах могут использоваться простые или сложные проценты, процентные или учетные ставки, различное число и схемы выплат и начисления процентов, дополнительные условия кредитования типа авансовых платежей, льготных периодов, возможных конверсий или консолидаций и многое другое, что финансовый менеджер должен учитывать при разработке схем финансирования и планов погашения кредитов.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник