что такое рекурсия javascript
Функциональное программирование с точки зрения EcmaScript. Рекурсия и её виды
Сегодня мы продолжим наши изыскания на тему функционального программирования в разрезе EcmaScript, на спецификации которого основан JavaScript. В предыдущих статьях цикла были рассмотрены следующие темы:
Рекурсия
Реку́рсия — определение, описание, изображение какого-либо объекта или процесса внутри самого этого объекта или процесса, то есть ситуация, когда объект является частью самого себя. Термин «рекурсия» используется в различных специальных областях знаний — от лингвистики до логики, но наиболее применение находит в математике и информатике.
Применительно к программированию под рекурсией подразумевают процессы, которые вызывают сами себя в своём теле. Рекурсивная функция имеет несколько обязательных составляющих:
Выделим характерные составляющие рекурсивной функции. Терминальное условие
и правило движения по рекурсии
Важно осознавать, что рекурсия это не какая-то специфическая фича JS, а техника очень распространённая в программировании.
Рекурсивный и итеративный процессы
Рекурсию можно организовать двумя способами: через рекурсивный процесс или через итеративный.
Рекурсивный процесс мы с вами уже видели:
Итеративное решение задачи о факториале выглядело бы так:
Оба этих варианта это рекурсия. В обоих решениях есть характерные для рекурсии черты: терминальное условие и правило движения по рекурсии. Давайте разберём их отличия.
Рекурсивный процесс на каждом шаге запоминает действие. которое надо сделать. Дойдя до термального условия, он выполняет все запомненные действия в обратном порядке. Поясним на примере. Когда рекурсивный процесс считает факториал 6, то ему нужно запомнить 5 чисел чтобы посчитать их в самом конце, когда уже никуда не деться и рекурсивно двигаться вглубь больше нельзя. Когда мы находимся в очередном вызове функции, то где-то снаружи этого вызова в памяти хранятся эти запомненные числа.
Выглядит это примерно так:
Как видите, основная идея рекурсивного процесса — откладывание вычисления до конца.
Такой процесс порождает изменяемое во времени состояние, которое хранится «где-то» снаружи текущего вызова функции.
Думаю, вы помните, что в первой статье из цикла о Функциональном программировании мы говорили о важности имутабельности и отсутствия состояния. Наличие состояния порождает много проблем, с которыми не всегда легко справится.
Итеративный процесс отличается от рекурсивного фиксированным количеством состояний. На каждом своём шаге итеративный процесс считает всё, что может посчитать, поэтому каждый шаг рекурсии существует независимо от предыдущего.
Думаю, очевидно, что итеративный процесс потребляет меньше памяти. Следовательно, всегда при создании рекурсии следует использовать его. Единственное исключение: если мы не можем посчитать значение до достижения термального условия.
Древовидная рекурсия
Многие считают, что деревья и работа с ними это что-то очень заумное, сложное и не понятное простым смертным. На самом деле это не так. Любая иерархическая структура может быть представлена в виде дерева. Даже человеческое мышление подобно дереву.
Чтобы лучше понять древовидную рекурсию разберём простой и популярный пример — числа Фибоначчи.
Чи́сла Фибона́ччи — элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, … (последовательность A000045 в OEIS), в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел. Названы в честь средневекового математика Леонардо Пизанского (известного как Фибоначчи).
Математически довольно просто сформулировать описание (а ведь декларативное программирование и есть описание) данной последовательности:
Теперь давайте перейдём от математики к логическим рассуждениям(нам ведь нужно программную логику написать). Для вычисления fib(5) нам придётся вычислить fib(4) и fib(3). Для вычисления fib(4) нам придётся вычислить fib(3) и fib(2). Для вычисления fib(3) нам придётся вычислить fib(2) и так до тех пор пока мы не дойдём до известных значений (1) и (2) в нашей математической модели.
На какие мысли нас должны навести наши рассуждения? Очевидно, мы должны использовать рекурсию. Термальное условие можно сформулировать как n
Рекурсия в JavaScript
Что такое рекурсия в JS? Это способность функции вызвать саму себя в своем теле. Рекурсивная функция обязательно должна иметь условие завершения, иначе мы попадем в бесконечный цикл. Случайное создание бесконечного цикла переполнит стек вызовов и браузер зависнет. Поэтому новички держатся от рекурсии подальше, на всякий случай.
Пример вызова обычной функции
Пример бесконечного цикла при вызове рекурсивной функции.
Пример демонстрирует, что если функция вызывается в теле, то после того как она отработает, все начнется сначала. Так делать не нужно.
let x = 2;
function recursion() <
x++;
recursion();
>
Как применять рекурсию в JavaScript?
С помощью рекурсии выведем в консоль числа от 3 до 6, так мы добавим в код возможность выхода из функции. Объявим глобальную переменную x со значением 3. Создадим функцию recursion(), в теле которой будем увеличивать содержимое переменной на 1 (x++) и выводить текущее значение x в консоль console.log(x). Сначала выведется число 3, к нему прибавится единица, значение переменной x станет равной 4, она также выведется на экран. Затем к 4 снова прибавится единица, значение переменной станет равной 5-ти. Это действие будет повторяться до тех пор, пока в переменной не окажется число 6. Как только нам вернется x со значением 6, работа функции завершится.
let x = 3;
function recursion() <
x++;
console.log(x);
if (x > 5) <
return x;
>
recursion();
>
recursion();
В результате в консоль выведутся следующие числа:
Пример рекурсии с массивами
Найдем сумму элементов массива при помощи рекурсии.
function summa(array, sum) <
sum += array.shift();
Функция summa первым параметром принимает массив, элементы которого мы будем суммировать при её вызове. Во второй параметр мы будем передавать результат суммы, с нулевым первоначальным значением. При помощи метода shift удаляем из массива array первый элемент и возвращает его значение. В результате изменится длина массива. Удаленный элемент присвоим переменной sum.
// текущее значение переменной sum = 1
0+1=1 // первоначальное значение + удаленный первый элемент массива
Создаем условие, где выясняем, есть ли ещё элементы в массиве? Если длина массива не равна нулю, значит, в массиве ещё есть элементы.
А на третьем проходе, тоже самое проделываем с последним элементом. Таким образом, в переменную sum перекочевали все элементы массива.
Итого
Очень часто новички боятся решать задачи с помощью рекурсий. Но к счастью, в 90% случаях в программировании на JS вполне можно обойтись без рекурсий, например, заменив их циклами. Многие так и делают, не знают и не хотят ничего знать о рекурсиях. Что нужно изучать в JavaScript, чтобы с легкостью решать при решении задач, где что применять? Советую вам подобрать такой обучающий курс, где бы автор рассказал вам то, что он использует в своей практике программирования на JavaScript. Есть толковый видеокурс, где собрана уникальная практическая информация, которая необходима Вам для успешного освоения языка JavaScript.
Копирование материалов разрешается только с указанием автора (Михаил Русаков) и индексируемой прямой ссылкой на сайт (http://myrusakov.ru)!
Добавляйтесь ко мне в друзья ВКонтакте: http://vk.com/myrusakov.
Если Вы хотите дать оценку мне и моей работе, то напишите её в моей группе: http://vk.com/rusakovmy.
Если Вы не хотите пропустить новые материалы на сайте,
то Вы можете подписаться на обновления: Подписаться на обновления
Если у Вас остались какие-либо вопросы, либо у Вас есть желание высказаться по поводу этой статьи, то Вы можете оставить свой комментарий внизу страницы.
Порекомендуйте эту статью друзьям:
Если Вам понравился сайт, то разместите ссылку на него (у себя на сайте, на форуме, в контакте):
Комментарии ( 0 ):
Для добавления комментариев надо войти в систему.
Если Вы ещё не зарегистрированы на сайте, то сначала зарегистрируйтесь.
Copyright © 2010-2021 Русаков Михаил Юрьевич. Все права защищены.
Понимание рекурсии с помощью JavaScript
Russian (Pусский) translation by Ilya Nikov (you can also view the original English article)

Введение
Некоторые проблемы более естественным образом решаются с помощью рекурсии. Например, последовательность, подобная последовательности Фибоначчи, имеет рекурсивное определение. Каждое число в последовательности представляет собой сумму двух предыдущих чисел в последовательности. Проблемы, которые требуют, чтобы вы построили или пересекли древовидную структуру данных, также могут быть решены с помощью рекурсии. Обучение думать рекурсивно даст вам мощное умение решать такие проблемы.
В этом уроке я шаг за шагом приведу несколько рекурсивных функций, чтобы увидеть, как они работают, и показать методы, которые вы можете использовать для систематического определения рекурсивных функций.
Содержание:
Что такое рекурсия?
Вы берете линию один и говорите им «пожалуйста, держитесь». Затем вы берете линию два и ставите их на удержание. Затем вы поднимаете линию три и помещаете их в режим ожидания. Наконец, вы отвечаете на четвертую строку и говорите с вызывающим. Когда вы закончите с четвертым абонентом, вы повесите трубку и возьмете третий звонок. Когда вы закончите с третьим вызовом, вы повесите трубку и возьмете второй звонок. Когда вы закончите со вторым вызовом, вы повесите трубку и заберете первый звонок. Когда вы закончите этот звонок, вы можете, наконец, положить телефон.
Каждый из телефонных звонков в этом примере подобен рекурсивному вызову функции. Когда вы получаете звонок, он помещается в стек вызовов (в терминах кода). Если вы не можете выполнить звонок сразу, вы переводите вызов на удержание. Если у вас есть вызов функции, который не может быть сразу оценен, он остается в стеке вызовов. Когда вы можете ответить на звонок, он подбирается. Когда ваш код способен оценивать вызов функции, он выгружается из стека. Соблюдайте эту аналогию, просматривая приведенные ниже примеры кода.
Рекурсия с цифрами
Предположим, что у вас есть функция, которая будет суммировать числа от 1 до n. Например, если n = 4, сумма будет равна 1 + 2 + 3 + 4.
Сначала мы определяем базовый случай. Обнаружение базового случая можно также рассматривать как поиск случая, когда проблема может быть решена без рекурсии. В этом случае, когда n равно нулю. 0 не имеет частей, поэтому наша рекурсия может остановиться, когда мы достигнем 0.
Это то, что происходит на каждом шагу:
Это еще один способ увидеть, как функция обрабатывает каждый вызов:
Аргумент должен измениться в рекурсивном случае и приблизит вас к основному случаю. Этот аргумент должен быть протестирован в базовом случае. В предыдущем примере, поскольку мы вычитаем один из рекурсивного случая, мы проверяем, равен ли аргумент нулю в нашем базовом случае.
Задача
Рекурсия со списками
Повторение в списке похоже на повторение по числу, за исключением того, что вместо сокращения числа на каждом шаге мы уменьшаем список на каждом шаге, пока не дойдем до пустого списка.
Рассмотрим функцию sum, которая принимает список как входные данные и возвращает сумму всех элементов в списке. Это реализация для суммы функции:
Когда вы повторяетесь в списке, проверьте, не пуст ли он. В противном случае сделайте рекурсивный шаг в сокращенной версии списка.
Задача
Построение списков
Здесь функция eq возвращает true, если оба входа одинаковы. Функция cons использует элемент и список как входные данные и возвращает новый список с добавленным элементом к началу.
Мы будем проверять, совпадает ли первый элемент в списке с элементом, который мы хотим удалить. Если это так, удалите первый элемент из списка и верните новый список. Если первый элемент не равен элементу, который мы хотим удалить, мы берем первый элемент в списке и добавляем его на рекурсивный шаг. Рекурсивный шаг будет содержать список с удаленным первым элементом.
В ситуации, когда нам нужно создать список, мы берем первый элемент и добавляем его в рекурсивную часть нашего списка.
Задача
Обзор
Рекурсия похожа на итерацию. Любая функция, которую вы можете определить рекурсивно, также может быть определена с помощью циклов. Другие вещи, которые следует учитывать при использовании рекурсии, повторяются во вложенных списках и оптимизируют рекурсивные вызовы.
Отличным ресурсом для продолжения изучения рекурсии является книга The Little Schemer. Она учит вас мыслить рекурсивно, используя формат вопросов и ответов.
Что такое рекурсия javascript
В теле функции могут быть вызваны другие функции для выполнения подзадач.
Рекурсия используется для ситуаций, когда выполнение одной сложной задачи можно представить как некое действие в совокупности с решением той же задачи в более простом варианте.
Сейчас мы посмотрим примеры.
Эта глава предназначена для читателей, которые пока с этой темой незнакомы и хотят лучше разобраться в том, как работают функции.
Степень pow(x, n) через рекурсию
Её можно представить как совокупность более простого действия и более простой задачи того же типа вот так:
Этот алгоритм на JavaScript:
Общее количество вложенных вызовов называют глубиной рекурсии. В случае со степенью, всего будет n вызовов.
Максимальная глубина рекурсии в браузерах ограничена, точно можно рассчитывать на 10000 вложенных вызовов, но некоторые интерпретаторы допускают и больше.
Контекст выполнения, стек
Теперь мы посмотрим, как работают рекурсивные вызовы. Для этого мы рассмотрим, как вообще работают функции, что происходит при вызове.
У каждого вызова функции есть свой «контекст выполнения» (execution context).
Затем интерпретатор приступает к выполнению вложенного вызова.
Разберём происходящее с контекстами более подробно, начиная с вызова (*) :
Как видно из иллюстраций выше, глубина рекурсии равна максимальному числу контекстов, одновременно хранимых в стеке.
Обратим внимание на требования к памяти. Рекурсия приводит к хранению всех данных для неоконченных внешних вызовов в стеке, в данном случае это приводит к тому, что возведение в степень n хранит в памяти n различных контекстов.
Реализация возведения в степень через цикл гораздо более экономна:
Любая рекурсия может быть переделана в цикл. Как правило, вариант с циклом будет эффективнее.
Но переделка рекурсии в цикл может быть нетривиальной, особенно когда в функции, в зависимости от условий, используются различные рекурсивные подвызовы, когда ветвление более сложное.
Есть и другие применения, с которыми мы встретимся по мере изучения JavaScript.
Здесь мы постарались рассмотреть происходящее достаточно подробно, однако, если пожелаете, допустимо временно забежать вперёд и открыть главу info:debugging-chrome, с тем чтобы при помощи отладчика построчно пробежаться по коду и посмотреть стек на каждом шаге. Отладчик даёт к нему доступ.
Рекурсия
Время чтения: больше 15 мин
Обновлено 27 октября 2021
Кратко
Рекурсия — это что-то, что описывает само себя.
Представить рекурсию проще всего на примере зеркального коридора — когда напротив друг друга стоят два зеркала. Если посмотреть в одно, то в нём будет отражение второго, во втором — отражение первого и так далее.
В «Начале» Нолана есть момент с зеркальным коридором, когда в отражении зеркала видно отражение зеркала, в котором видно отражение зеркала, в котором видно.
Второй пример, чуть более академически правильный — это фрактал. Тот же треугольник Серпинского — это пример рекурсии, потому что часть фигуры — это одновременно вся фигура.
Треугольник состоит из 3 точно таких же треугольников.
Рекурсия в программировании
В программировании под рекурсией чаще всего понимают функцию, которая вызывает саму себя.
При решении некоторых задач мы можем обнаружить, что решение можно разбить на несколько простых действий и более простой вариант той же задачи.
Например, при возведении числа в степень мы берём число, умножаем его на себя несколько раз. Эту операцию можно представить в виде:
Но это же можно представить в виде нескольких последовательных умножений на 2:
При таком представлении всё возведение в степень — это лишь умножение предыдущего результата на 2:
Именно такие задачи называются рекурсивными — когда часть условия ссылается на всю задачу в целом (или похожую на неё).
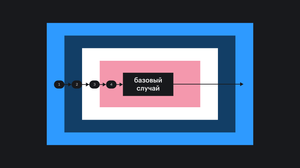
У рекурсии 2 составляющие: повторяющиеся операции и базовый случай.
Повторяющиеся операции
В примере с возведением в степень повторяющиеся операции — это умножение.
Такие операции могут быть сложными и включать в себя несколько подзадач. Такое, например, часто встречается в математике.
Базовый случай
Вторая важная часть рекурсии — это базовый случай.
Базовый случай — это условие, при выполнении которого рекурсия заканчивается и функция больше не вызывает саму себя.
Например, при возведении в степень базовый случай наступает, когда значение степени становится равно искомому.
Как только выполнение доходит до базового случая, оно останавливается.
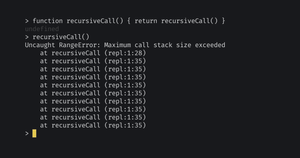
Без базового случая любая рекурсивная функция уйдёт в бесконечное выполнение, потому что будет вызывать себя без конца.
В JS это приводит к переполнению стека вызовов, и функция останавливается с ошибкой.
Если выполнить функцию без базового случая, которая лишь вызывает себя, получим ошибку.
Цикл и рекурсия
Из-за повторяющихся операций рекурсия схожа с циклом. Их часто считают взаимозаменяемыми, но это всё же не совсем так.
Рекурсия проигрывает циклу в следующем:
Цикл же проигрывает рекурсии в таких вещах:
Поэтому на вопрос «Что использовать: рекурсию или цикл?» ответом будет «Зависит от задачи», серебряной пули здесь нет :–)
Давайте решим одну и ту же задачу с использованием цикла и рекурсии, чтобы увидеть разницу в подходах. Будем писать функцию для нахождения факториала.
Факториал числа — это произведение всех чисел от единицы до этого числа. Например, факториал 5 — это произведение (1 × 2 × 3 × 4 × 5) = 120.
Факториал с помощью цикла
Сперва решим задачу нахождения факториала с помощью цикла.
В этой функции мы используем цикл, чтобы умножить каждое число на результат предыдущего умножения. То же самое мы можем сделать и рекурсивно.
Факториал с помощью рекурсии
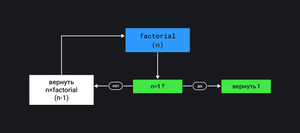
Для расчёта факториала рекурсивно мы создадим функцию, в которой в первую очередь опишем базовый случай, а уже потом — повторяющиеся действия.
Хорошим правилом при работе с рекурсией считается первым делом описывать базовый случай (как ранний выход, early return) и только потом — всё остальное. Это позволяет сделать работу с рекурсией безопаснее.
В виде блок-схемы мы можем представить алгоритм факториала как условие и под-вызов той же функции.
Кроме того, что функция стала заметно короче, она теперь выражает непосредственно математическую суть факториала.
Разберём по шагам, что происходит с переменной n и результатом функции factorial после каждого вызова:
Минусы такой реализации:
Рекурсивные структуры данных
Раньше мы упомянули, что в программировании чаще всего под рекурсией понимают функцию, которая вызывает сама себя. Но кроме рекурсивных функций ещё есть рекурсивные структуры данных.
Структура данных — это контейнер, который хранит данные в определённом формате. Этот контейнер решает, каким образом внешний мир может эти данные считать или изменить.
Структуры данных, части которых включают в себя такие же структуры, называются (вы угадали) рекурсивными. Работать с такими структурами в цикле не очень удобно. Чтобы понять почему, рассмотрим пример одной из рекурсивных структур данных — дерева.
Деревья
Дерево — это структура, в которой у каждого узла может быть несколько дочерних подузлов — «детей».
Мы уже встречались с деревьями в статье «Как браузер рисует страницы». Мы рассматривали DOM, CSSOM и Render Tree. Вспомним, как выглядит DOM-дерево.
Работать с деревьями с помощью циклов (итеративно) неудобно. Представьте, что мы хотим получить названия всех элементов на странице. Да, мы можем пройтись циклом по 1-му уровню или 2-му, но дальше нужно думать, как определять, где мы были, где ещё нет и куда идти дальше.
С рекурсией обход дерева становится немного проще.
Рекурсивный обход
В случае с рекурсией мы можем придумать например такой алгоритм для обхода дерева:
Когда использовать рекурсию
Сама по себе рекурсия — это всего лишь инструмент. Нет чётких правил, когда её надо использовать, а когда — нет. Есть лишь некоторые рекомендации.