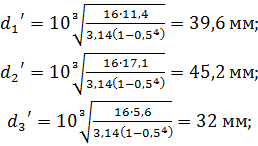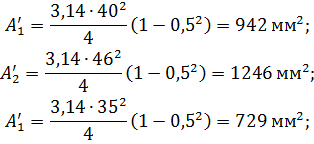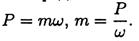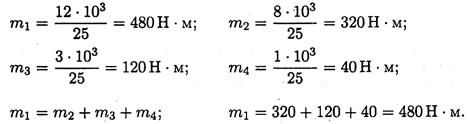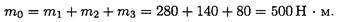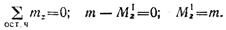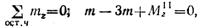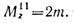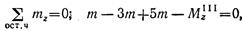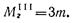что такое рациональное расположение колес на валу
Выполнение контрольной, курсовой, типовой работы по математике, физике, информатике, графике
Строим эпюру крутящих моментов. Заметим, что скачок на эпюре всегда численно равен приложенному вращающему момену.
Выбираем соответствующий масштаб.
Откладываем значения моментов, штрихуем эпюру поперек, обводим по контуру, записываем значения моментов (см. эпюру под схемой вала (рис. 26.3)). Максимальный крутящий момент на участке Ш МКз = 320 Н·м.
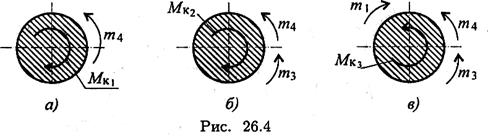
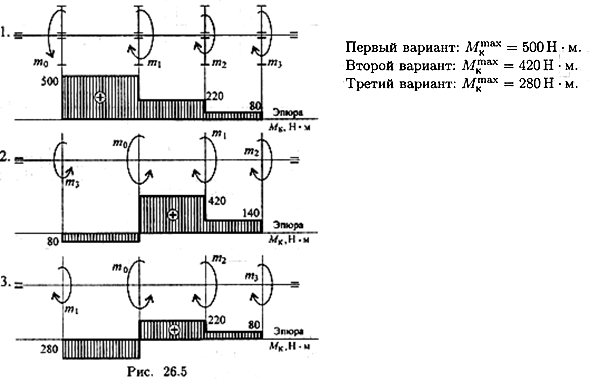
Пример 2. Выбрать рациональное расположение колес на валу (рис. 26.5). m1 = 280 Н·м; m2 = 140 Н·м; m3 = 80 Н·м.
Примечание. Меняя местами колеса (шкивы) на валу можно изменять величины крутящих моментов. Рациональным р. положением является такое, при котором крутящие моменты принимают минимальные из возможных значения.
mo = m1 + m2 + m3 = 280 + 140 + 80 = 500 Н·м.
Рассмотрим нагрузки на валу при различном расположении колес.
Из представленных вариантов наиболее рационально расположение шкивов в третьем случае, здесь значения крутящих моментов минимальны. Вывод: при установке шкивов желательно, чтобы мощность подавалась в середине вала и по возможности равномерно распределялась направо и налево.
Первый вариант: 
.
Второй вариант: 
.
Третий вариант: 
.
Расчет на прочность при кручении
Практическое занятие 5
Расчет на прочность при кручении
К выполнению задания необходимо приступить после изучения темы
2.4. «Сдвиг и кручение».
Цель:научиться определять диаметр вала из условия прочности и жесткости при кручении.
Краткие теоретические сведения
Условие прочности при кручении
Проектировочный расчёт, определение размеров поперечного сечения
Условие жёсткости при кручении
Проектировочный расчет определения наружного диаметра
АЛГОРИТМ ВЫПОЛНЕНИЯ
1. Построить эпюру крутящих моментовпо длине вала для предложенной в задании схемы.
2. Выбрать рациональное расположение колес на валуи дальнейшие расчеты проводить для вала с рационально расположенными шкивами.
(Рациональное расположение колёс – расположение, при котором максимальное значение крутящего момента на валу – наименьшее из всех возможных.) Для экономии металла сечение бруса рекомендуется выполнить кольцевым
3. Определить потребные диаметры вала круглого и кольцевого сечения из расчета на прочность и жесткость и выбрать наибольшее из полученных значений, округлив величину диаметра.
4. Сравнить затраты металла для случая круглого и кольцевого сечений. Сравнение провести по площадям поперечных сечений валов. 
Площади валов рассчитать в наиболее нагруженном сечении (по максимальному крутящему моменту на эпюре моментов).
Пример. Для заданного бруса (рис. 28.1) построить эпюры крутящих моментов, рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента. Построить эпюру крутящих моментов при рациональном расположении шкивов.
Из условия прочности определить диаметры вала для сплошного и кольцевого сечений, приняв 
Сравнить полученные результаты по полученным площадям поперечных сечений. [τк] = 35 МПа.
Решение
1. Пользуясь методом сечений, определяем крутящие моменты на участках вала (рис. 28.2).
Сечение 1 (рис. 28.2а):
Сечение 2 (рис. 28.2б):
Сечение 3 (рис. 28.2в):
2. Строим эпюру крутящих моментов. Значения крутящих моментов откладываем вниз от оси, т. к. моменты отрицательные.
Максимальное значение крутящего момента на валу в этом случае 1000Н . м (рис. 28.1).
3. Выберем рациональное расположение колес на валу. Наиболее целесообразно такое размещение колес, при котором наибольшие положительные и отрицательные значения крутящих моментов на участках будут по возможности одинаковыми. Из этих соображений ведущий шкив, передающий момент 1000Н . м, помещаем ближе к центру вала, ведомые шкивы 1 и 2 размещаем слева от ведущего с моментом 1000Н·м, шкив 3 остается на том же месте. Строим эпюру крутящих моментов при выбранном расположении шкива (рис. 28.3).
Максимальное значение крутящего момента на валу при выбранном расположении колес на валу 600 Н·м.
Условие прочности при кручении 
Момент сопротивления кручению
Определяем диаметры вала по сечениям:
Округляем полученные значения: d1 = 40 мм; d2 = 45 мм; d3 = 35 мм.
Моменты сопротивления остаются теми же, По условию
Полярный момент сопротивления кольца
Формула для определения наружного диаметра вала кольцевого сечения будет следующей:
Расчет можно провести по формуле
Диаметры вала по сечениям:
Наружные диаметры вала кольцевого сечения практически не изменились.
6. Для вывода об экономии металла при переходе на кольцевое сечение сравним площади сечений (рис. 28.4).
Сплошное круглое сечение:
При условии, что сечение – кольцо, (рис. 28.46):
Сравнительная оценка результатов:
Следовательно, при переходе с кругового на кольцевое сечение экономия металла по весу составит 1,3 раза.
Задание:
1.Для стального вала круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям.
2.Построить эпюру крутящих моментов по длине вала.
3.Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
4.Построить эпюру крутящих моментов для этого случая.
5.Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
6.Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного или оканчивающегося на 5 числа.
Данные взять из таблицы 7, схема 7.
| Параметр | Вариант | |||||||||
| a = b = c, м | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 |
| P1, кВт | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 |
| P2, кВт | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 |
| P3, кВт | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | 4,0 |
1.  | 2.  |
3.  | 4.  |
5.  | 6.  |
| 7. | 8. |
| 9. | 10. |
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| ПЗ. |
| Разраб. |
| Провер. |
| Лит. |
| Листов |
Цель: _______________________________________________________________
Оборудование (приборы, материалы, дидактическое обеспечение)_________________________________________________________
Компьютерная программа (если используется): Наименование программы_________________________________________________________
Дано:
Определить:
Провести расчет для вала кольцевого сечения, приняв с = 0,9.
Сделать выводы о целесообразности выполнения вала круглого или кольцевого сечения, сравнив площади поперечных сечений.
Решение:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| ПЗ |
Контрольные вопросы:
1.Какие деформации возникают при кручении? ___________________________
2.Какие гипотезы выполняются при деформации кручения? ________________
3.Изменяются ли длина и диаметр вала после скручивания?_________________
Какие внутренние силовые факторы возникают при кручении? ____________
Что такое рациональное расположение колес на валу? ____________________
Как изменится напряжение в сечении, если диаметр вала уменьшить в два раза?_________________________________________________________________________________________________________________________________________________________________________________________________________________
Проведены расчеты вала на прочность и жесткость. Получено: диаметр вала из расчета на прочность 65 мм, диаметр вала из расчета на жесткость 70 мм. Каким должен быть вал?________________________________________________________
Как изменится угол закручивания вала, если крутящий момент увеличить в 4 раза, а диаметр уменьшить в 2 раза?____________________________________________
Напишите условия прочности и жесткости при кручении.______________________
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| ПЗ |
Чему равен крутящий момент в сечении?___________________________________
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
ИМПЕРАТОРА АЛЕКСАНДРА I»
(ФГБОУ ВПО ПГУПС)
ПЕТРОЗАВОДСКИЙ ФИЛИАЛ
Практическое занятие 6
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
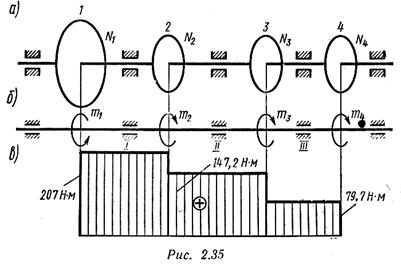
Решение. 1. Определяем моменты пар сил на шкивах
1. Определяем моменты пар сил на шкивах.
Вращающий момент определяем из формулы мощности при вращательном движении
Момент на шкиве 1 движущий, а моменты на шкивах 2, 3, 4 — моменты сопротивления механизмов, поэтому они имеют противоположное направление. Брус скручивается между движущим моментом и моментами сопротивления. При равновесии момент движущий равен сумме моментов сопротивления:
2. Определяем крутящие моменты в поперечных сечениях бруса с помощью метода сечений.
 |
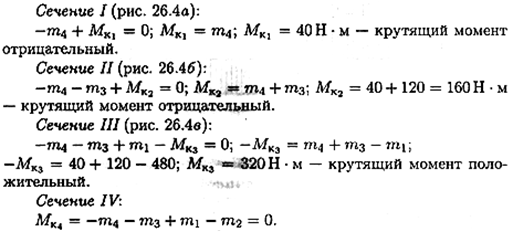3. Строим эпюру крутящих моментов. Заметим, что скачок на эпюре всегда численно равен приложенному вращающему моменту.
Выбираем соответствующий масштаб.
Откладываем значения моментов, штрихуем эпюру поперек, обводим по контуру, записываем значения моментов (см. эпюру под схемой вала (рис. 26.3)). Максимальный крутящий момент на участке III Мкз = 320 Н*м.
Пример 2. Выбрать рациональное расположение колес на валу (рис. 26.5). m1 = 280 Н • м; т2 = 140 Н • м; т3 = 80 Н* м.
Примечание. Меняя местами колеса (шкивы) на валу, можно изменять величины крутящих моментов. Рациональным расположением является такое, при котором крутящие моменты принимают минимальные из возможных значения.
Рассмотрим нагрузки на валу при различном расположении колес.
Из представленных вариантов наиболее рационально расположение шкивов в третьем случае, здесь значения крутящих моментов минимальны. Вывод: при установке шкивов желательно, чтобы мощность подавалась в середине вала и по возможности равномерно распределялась направо и налево.
Пример 3. Для бруса, изображенного на рис. 2.34, а, построить эпюру крутящих моментов.
Решение
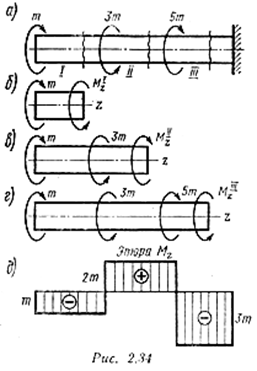
1. Заданный брус имеет три участка I, II, III. Напомним, что границами участков являются сечения, в которых прилажены внешние (скручивающие) моменты.
В данном случае проще, применяя метод сечений, оставлять левую и отбрасывать правую часть бруса — это дает возможность не определять реактивный момент в заделке.
Проводим произвольное поперечное сечение на участке I и составляем уравнение равновесия для оставленной части бруса, изображенной отдельно на рис. 2.34, 6:
В любом сечении участка I крутящий момент имеет найденное значение M 1 z = т. Из уравнения равновесия для оставленной части значение M 1 z получилось со знаком плюс. Это указывает на то, что выбранное направление M 1 z соответствует действительному.
Эпюра крутящих моментов на этом участке — прямая, параллельная оси абсцисс. Согласно принятому правилу знаков М 1 я отрицателен, и ординаты эпюры откладываем вниз от ее оси.
2. Проводим произвольное поперечное сечение на участке II и составляем уравнение равновесия для оставленной части бруса, изображенной отдельно на рис. 2.34, в:
И в этом случае выбранное направление M II z соответствует действительному. В любом сечении участка II крутящий момент Mz II = 2m. Согласно принятому правилу знаков, Mz II положителен и ординаты эпюры откладываем вверх от ее оси.
3. Проводим произвольное поперечное сечение на участке III и составляем уравнение равновесия для оставленной части бруса, изображенной отдельно на рис. 2.34, г:
В любом сечении участка III Mz III = —Зт.
Эпюра крутящих моментов представлена на рис. 2.34, д.
При нагружении бруса сосредоточенными моментами эпюра всегда имеет такой же характер, как и в рассматриваемом случае: на отдельных участках она ограничена прямыми, параллельными оси абсцисс; в местах приложения внешних (скручивающих) моментов получаются скачки на величину этих моментов.
Пример 4. На вал насажены шкивы 1, 2, 3, 4 (рис. 2.35, а). Шкив 1 передает от источника энергии на вал мощность N1 = 5,2 кВт, а остальные шкивы снимают с вала и передают рабочим машинам мощности соответственно N2 = 1,5 кВт; N3 = 1,7 кВт; N4 = 2,0 кВт. Вал вращается с частотой п = 240 об/мин. Построить эпюру крутящих моментов.
Техническая механика. Конспекты лекций (стр. 11 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
При рассмотрении правой части из условия ее равновесия мы получили бы, естественно, тот же результат: 
Аналогично вычисляется крутящий момент в поперечных сечениях на втором участке вала между шкивами I и III 
, а на третьем участке между шкивами III и IV 
Итак, крутящий момент в каком-либо поперечном сечении вала численно равен алгебраической сумме моментов внешних пар, действующих на вал в плоскостях, перпендикулярных оси вала, и приложенных по одну сторону от рассматриваемого сечения. Эпюру крутящих моментов строят аналогично эпюре продольных сил, откладывая от горизонтали (рис. 42б) ординаты, пропорциональные крутящим моментам в поперечных сечениях соответствующих участков вала.
Знак крутящего момента в поперечном сечении вала определяется исходя из направления внешних моментов. Крутящий момент положителен, когда внешние моменты вращают отсеченную часть по часовой стрелке, если смотреть со стороны проведенного сечения. Положительные ординаты эпюры крутящих моментов откладывают вверх, отрицательные — вниз от горизонтальной линии, называемой осью, или базой, эпюры.
Рациональное расположение колес на валу
Выберем рациональное расположение колес на вал, если заданы моменты: m1=280 н*м, m2=140 Н*м, m3=80 Н*м. Меняя местами колеса (шкивы) на валу, можно изменять величины крутящих моментов. Рациональным расположением является такое, при котором крутящие моменты принимают минимальные из всех возможных значений.
m0= m1+m2+m3=280+140+80=500 Н*м.
Рассмотрим нагрузки на валу при различном расположении колес:
Из представленных вариантов наиболее рационален третий вариант, где значение крутящего момента минимально. Вывод: при установке шкивов желательно, чтобы мощность подавалась в середине вала и по возможности равномерно распределялась налево и направо.
Рис. 43 Рациональное расположение колес на валу.
Под изгибом понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают изгибающие моменты (рис. 44). Элементы конструкций, работающих на изгиб, называют балками.
Рис. 44 Изгиб. Н. л. – нейтральная линия
Если изгибающий момент является единственным силовым фактором, а поперечные и нормальные силы отсутствуют, то такой изгиб называется чистым.
В большинстве случаев в поперечных сечениях бруса наряду с изгибающими моментами возникают поперечные силы. В этом случае изгиб называют поперечным.
Если же силы, вызывающие деформацию изгиба, действуют в плоскости, проходящей через ось балки, но не проходящей через одну из главных центральных осей ее поперечного сечения, имеет место косой изгиб.
Лекция № 23 «Эпюры поперечных сил и изгибающих моментов»
1. Эпюры поперечных сил и изгибающих моментов.
Определим внутренние силовые факторы в сечениях балки АВ (рис. 45,а), на которую действуют сосредоточенные силы
, перпендикулярные к ее оси. Эти силы вызывают вертикальные реакции
опор балки. Горизонтальная составляющая реакции шарнирно-неподвижной опоры при действии только вертикальных сил, перпендикулярных к оси балки, очевидно, равна нулю. Опорные реакции
могут быть определены из уравнений равновесия, составленных для всех сил, действующих на балку. Проведем мысленно произвольное поперечное сечение С на расстоянии z от левой опоры и рассмотрим условия равновесия левой и правой отсеченных частей балки (рис.45,б и в). Левая часть должна находиться в равновесии под действием внешних сил
и внутренних сил, возникающих в сечении С. Правая часть должна находиться в равновесии под действием внешних сил
и внутренних сил в проведенном сечении С.
Согласно закону равенства действия и противодействия, внутренние силы по сечению С для левой и правой частей одинаковы, но направлены в противоположные стороны. Внутренние силы в любом сечении балки могут быть заменены силой Q и парой сил с моментом М. Сила Q называется поперечной силой, а момент М — изгибающим моментом в поперечном сечении балки.
Для сил, действующих на левую отсеченную часть балки (рис.45,б), составим уравнение равновесия. Уравнение проекций на вертикальную ось у (рис.45,б):
уравнение моментов относительно точки С:
Решив первое из этих уравнений относительно Q, а второе относительно М, получим:
Итак, величины поперечной силы и изгибающего момента в любом поперечном сечении балки могут быть определены по известным внешним силам, действующим на балку.
Поперечная сила Q и момент пары М действуют на сечение левой и правой отсеченных частей балки в противоположных направлениях (рис.45,б). Чтобы при вычислении изгибающего момента М и поперечной силы Q в каком-либо поперечном сечении балки по внешним силам, действующим слева или справа от этого сечения, получить значения, одинаковые не только по величине, но и по знаку, следует установить противоположные правила знаков для сил и их моментов слева и справа от сечения.
Установим правило знаков для изгибающих моментов и поперечных сил.
Рис. 46 Правило знаков
Когда внешняя сила, расположенная слева от сечения, вращает относительно центра тяжести сечения по ходу часовой стрелки, то изгибающий момент считают положительным (рис.46,а). При противоположном направлении изгибающий момент считают отрицательным (рис.46,б).
Для поперечной силы знак также связан с характером деформации. Когда внешние силы действуют слева от сечения вверх, а справа — вниз, поперечная сила положительна (рис.46,в). При противоположном действии внешних сил, т. е. слева от сечения вниз, а справа — вверх, поперечная сила отрицательная (рис.46,г).
Внутренние силовые факторы в сечениях балок — поперечная сила Q и изгибающий момент М — зависят от внешней нагрузки и изменяются по длине балки. Законы их изменения представляются некоторым уравнениями, где аргументами являются координаты z поперечных сечений балки, а функциями — Q или М. Эти уравнения удобно представлять в виде эпюр, ординаты которых для любых значений абсциссы z дают соответствующие значения изгибающего момента М или поперечной силы Q. Эпюры изгибающих моментов и поперечных сил строятся аналогично эпюрам продольных сил и крутящих моментов. При построении эпюр положительные значения поперечных сил и моментов откладывают вверх от оси, отрицательные — вниз; ось (или базу) эпюры проводят параллельно оси балки.
Тема 2.7 Сочетание основных деформаций. Изгиб с растяжением или сжатием. Изгиб и кручение. Гипотезы прочности
Лекция № 24 «Сочетание основных деформаций»
1. Гипотезы прочности
2. Изгиб и кручение
1 Гипотезы прочности
Сложное деформированное состояние возникает в тех случаях, когда элемент конструкции или машина подвергается одновременно нескольким простейшим деформациям.
В заклепочных и шпоночных соединения одновременно возникают срез и смятие и соответственно действуют нормальные и касательные напряжения. В затянутых болтах также имеет место сложное деформирование, в них обнаруживается совместное действие растяжения от затяжки силой F и кручения от момента трения Мк. В связи с этим в болтах возникают нормальные напряжения от растяжения и касательные напряжения от кручения
где 
— площадь сечения болта; 
— полярный момент сопротивления.
Нормальные напряжения распределены по сечению равномерно, а касательные достигают максимальных значений у контура болта. Очевидно, периферийные точки болта находятся в наиболее опасном состоянии, особенно в связи с наличием концентрации напряжений в нарезке.
Другим примером сложного деформирования являются валы, которые работают на изгиб и кручение. При этом в поперечном сечении вала возникают нормальные и касательные напряжения. Возникающие от изгиба нормальные напряжения достигают максимального значения в волокнах, наиболее удаленных от нейтральной оси:
где Ми — изгибающий момент; 
— осевой момент сопротивления сечения.