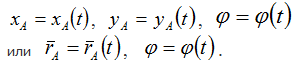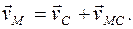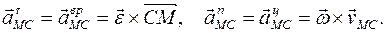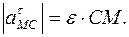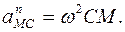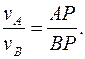что такое плоское движение тела

iSopromat.ru

Определение плоского движения

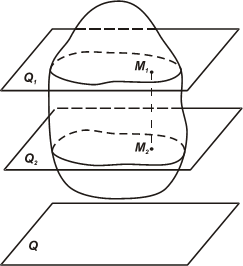
Плоским движением твердого тела называется такое его движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости (рис. 1.1).

То есть точки М₁ и М₂ тела А, например, двигаются в плоскостях Q₁ и Q₂, соответственно параллельных плоскости Q.

Закон плоского движения

Если в первоначальной момент отрезок М₁М₂ перпендикулярен плоскостям Q, Q₁, Q₂, то и при последующем движении тела он остается параллельным своему первоначальному положению и перпендикулярным к этим плоскостям, т.е. движется поступательно.

Следовательно, скорости и ускорения всех точек тела, лежащих на отрезке М₁М₂, равны и одинаково направлены.

Это позволяет свести изучение движение отрезка М₁М₂ к изучению движения точки М₁ или М₂ вместе с соответствующим сечением тела в плоскости (рис. 1.2).

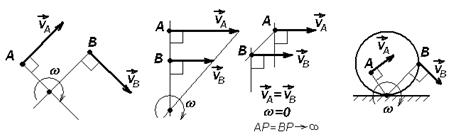
Положение фигуры в плоскости вполне определяется положением в этой плоскости какого-нибудь отрезка, например АВ, скрепленного с фигурой. Положение отрезка будет вполне определено, если будет известно положение какой-либо точки, например А (полюс), и угла наклона ( φ ) отрезка к выбранной оси.

Тогда закон движения фигуры в плоскости может быть записан в виде

В учебной литературе показано, что закон вращательного движения не зависит от выбора полюса.

Источник

Теоретическая механика

24. Плоскопараллельное (плоское) движение твердого тела.

Движение абсолютно твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой заданной неподвижной плоскости, называется плоскопараллельным. Другими словами, прямая, лежащая в плоскости сечения, в процессе движения тела не покидает этой плоскости.

Таким образом, плоское движение твердого тела полностью определяется движением плоской фигуры, образованной в результате сечения тела плоскостью. В дальнейшем, под плоским движением твердого тела будем понимать движение плоской фигуры в заданной плоскости.

Соотношение между скоростями точек плоской фигуры

В итоге можно утверждать, что плоское движение может быть рассмотрено как сумма двух движений: поступательное движение со скоростью и вращательное движение вокруг оси перпендикулярной плоскости движения.

Теперь докажем важную теорему, связывающую модули скоростей двух, произвольно выбранных точек плоской фигуры.

Теорема. Проекции скоростей двух точек плоской фигуры на прямую, соединяющую эти точки, равны.

Из равенства левых частей уравнений следует равенство их правых частей, то есть

Источник

Плоское движение твердого тела

1.4.1. Описание плоского (плоскопараллельного) движения (ППД) твердого тела

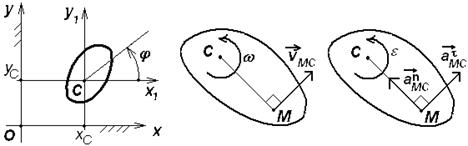
Движение плоской фигуры можно рассматривать как сложное движение тела, являющимся результатом сложения поступательного движения плоской фигуры вместе с полюсом С и её вращательного движения вокруг полюса С.

Поступательное движение фигуры вместе с полюсом рассматривается как переносное, вращательное вокруг полюса – как относительное её движение.

Рис. 6. Плоская фигура. Скорость и ускорение точки

1.4.2. Скорость точки плоской фигуры:

,

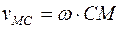
где ω – величина угловой скорости плоской фигуры. Вектор 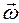направлен перпендикулярно плоскости движения.

Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны между собой.

1.4.3. Ускорение точки плоской фигуры равно сумме векторов ускорения полюса и ускорения этой точки при её вращении вокруг полюса:

,

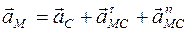
где

Касательное (вращательное) ускорение 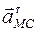направлено перпендикулярно отрезку МС в сторону ускорения вращения плоской фигуры вокруг полюса С (рис. 6,в). Его величина равна

Вектор нормального (центростремительного) ускорения 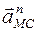направлен от точки М к полюсу С; его величина равна

Если найдено положение МЦС (точки Р), то движение плоской фигуры в каждый момент времени можно рассматривать как мгновенно-вращательное вокруг центра Р. Тогда скорость точки А плоской фигуры вычисляется по формуле 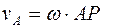и направлена перпендикулярно отрезку АР в сторону вращения плоской фигуры вокруг МЦС. Величины скоростей точек плоской фигуры пропорциональны расстояниям от этих точек до МЦС:

Положение МЦС можно найти на пересечении перпендикуляров к скоростям двух её точек (А и В), восстановленных из этих точек (рис. 7,а). Перпендикуляры могут совпадать (рис. 7,б) или не пересекаться. В последнем случае (рис. 7в) МЦС находится в бесконечно удаленной точке, скорости точек плоской фигуры одинаковы, угловая скорость её равна нулю.

Положение МЦС может определяться и непосредственно из специального кинематического условия движения. Например, если колесо катится без скольжения по неподвижной направляющей, то мгновенный центр скоростей находится в точке касания колеса с направляющей (рис. 7,г).

Рис.7. Положение мгновенного центра скоростей

Источник

Плоское движение твердого тела

16) Сложным движением точки

Сложным движением точки называется такое ее движение, при котором она движется относительно системы отсчета, перемещающейся по отношению к некоторой другой системе отсчета, принятой за неподвижную. Например, можно считать, что пассажир, идущий по вагону движущегося поезда, совершает сложное движение по отношению к полотну дороги, состоящее из движения пассажира по отношению к вагону (подвижная система отсчета) и движения пассажира вместе с вагоном по отношению к полотну дороги (неподвижная система отсчета).

Движение точки, обусловленное движением подвижной системы координат, называется переносным движением точки.

В приведенном выше примере движение пассажира относительно вагона будет относительным, а скорость – относительной скоростью пассажира; движение вагона по отношению к полотну дороги будет для пассажира переносным движением, а скорость вагона, в котором находится пассажир, будет в этот момент его переносной скоростью; наконец, движение пассажира по отношению к полотну будет его абсолютным движением, а скорость – абсолютной скоростью.

Источник

Плоское движение твердого тела

Плоским (плоскопараллельным) назыв. такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости. Уравнения плоского движения: x_A= f₁(t), y_A= f₂(t), j = f₃(t), точка А назыв. полюсом. Плоское движение тв.тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А),и из вращательного движения вокруг этого полюса. Поступательное перемещение зависит от выбора полюса, а величина и направление угла поворота не зависят.

Плоским движением твердого тела называется такое его движение, при котором каждая его точка все время движется в одной и той же плоскости.

Плоскости, в которых движутся отдельные точки тела, параллельны между собой и параллельны одной и той же неподвижной плоскости. Плоское движение твердого тела часто называют плоскопараллельным. Траектории точек тела при плоском движении являются плоскими кривыми.

Плоское движение твердого тела имеет большое значение в технике. Вращательное движение твердого тела вокруг неподвижной оси является частным случаем движения твердого тела.

При изучении плоского движения, как и любого другого, необходимо рассмотреть способы задания этого движения, а также приемы вычисления скоростей и ускорений точек тела.

Если в теле провести некоторую прямую О₁О₂, перпендикулярную плоскостям, в которых происходит движение точек, то все точки этой прямой будут двигаться по одинаковым траекториям с одинаковыми скоростями и ускорениями; сама прямая будет, естественно, сохранять свою ориентацию в пространстве. Таким образом, при плоском, движении твердого тела достаточно рассмотреть движение одного из сечений тела.

Сечение твердого тела будем называть плоской фигурой. Положение фигуры на ее плоскости полностью определяется положением отрезка прямой линии, жестко скрепленной с этой плоской фигурой.

Уравнения плоского движения твердого тела

Для задания положения плоской фигуры на плоскости относительно системы координат , лежащей в плоскости фигуры, достаточно задать на этой плоскости положение отрезка АВ, скрепленного с фигурой.

Положение отрезка АВ, относительно системы координат определяется заданием координат какой-нибудь точки этого отрезка и его направления. Например, координаты точки А ( ) и направление, заданное углом .

Уравнения движения плоской фигуры относительно системы координат имеют вид: .

Твердое тело при плоском движении имеет три степени свободы.

называются уравнениями плоского движения твердого тела.

Перейдем к изучению движения отдельной точки твердого тела. Положение любой точки М плоской фигуры относительно подвижной системы отсчета ,скрепленной с этой движущейся фигурой и лежащей в ее плоскости, полностью определяется заданием координат x и y точки М (Рис.6-3).

Между координатами точки М в различных системах отсчета существует связь:

, (6-1)

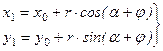
где — длина отрезка ОМ, — постоянный угол между ОМ и осью . С учетом выражений и получаем

, (6-2)

Формулы (6-2) являются уравнениями движения точки М плоской фигуры относительно координат . Эти формулы позволяют определить координаты любой точки плоской фигуры по заданным уравнениям движения этой фигуры и координатам этой точки относительно подвижной системы отсчета, скрепленной с движущейся фигурой.

Используя матрично-векторные обозначения уравнения (6-2) можно записать в такой форме:

, (6-3)

где А – матрица поворота на плоскости:

, , , .

Разложение плоского движения на поступательное

И вращательное движения.

Теорема. Любое движение твердого тела, в том числе и движение плоской фигуры в ее плоскости, бесчисленным множеством способов можно разложить на два движения, одно из которых переносное, а другое – относительное.

В частности, движение плоской фигуры в ее плоскости относительно системы , расположенной в той же плоскости, можно разложить на переносное и относительное движения следующим образом. Примем за переносное движение фигуры ее движение вместе с поступательно движущейся системой координат , начало которой скреплено с точкой О фигуры, принятой за полюс. Тогда относительное движение фигуры будет по отношению к подвижной системе координат вращением вокруг подвижной оси, перпендикулярной плоской фигуре и проходящей через выбранный полюс.

Для доказательства этого достаточно показать, что плоскую фигуру в ее плоскости из одного положения в любое другое можно перевести двумя перемещениями – поступательным перемещением в плоскости фигуры вместе с каким –либо полюсом и поворотом в той же плоскости вокруг этого полюса.

Рассмотрим два любых положения плоской фигуры 1 и 2. Выделим отрезок АB в рассматриваемой фигуре. Перевод фигуры из положения 1 в положение 2 можно рассматривать как суперпозицию двух движений: поступательного из 1 в 1′ и вращательного из 1′ в 2 вокруг точки A’, называемой обычно полюсом (рис. 6-4а). Существенно, что в качестве полюса можно выбрать любую точку, принадлежащую фигуре или даже лежащую в плоскости вне фигуры. На рис. 6-4б, к примеру, в качестве полюса выбрана точка В. Обратите внимание: длина пути при поступательном перемещении изменилась (в данном случае увеличилась), но угол поворота остался прежним!

Источник