что такое отрезок в математике 2 класс
Основы геометрии
Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
Познакомимся с основными геометрическими понятиями, изучаемыми в начальной школе.
Точка
Точка — это основная и самая простая геометрическая фигура.
В геометрии точка обозначается заглавной латинской буквой или цифрой. Многие латинские буквы по написанию похожи на английские буквы.
В тексте точку обозначают следующим символом: « (·) A » — точка « А ».
Прямая
Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.
Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.
Способы обозначения прямых
Способы обозначения лучей
Отрезок
Основное свойство отрезка — это его длина.
Длина отрезка — это расстояние между его концами.
В математике отрезок обозначается заглавными латинскими буквами.
Ломаная
Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.
Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.
Звенья ломаной — это отрезки ломаной.
В математике ломаная обозначается заглавными латинскими буквами.
Чтобы найти длину ломаной, необходимо сложить длины всех её звеньев (отрезков), из которых она состоит.
KLCM = KL + LC + CM = 3 см + 2 см + 2 см = 7 см
Вот мы и познакомились с основами геометрии. Теперь мы готовы рассмотреть не менее важную геометрическую фигуру — угол.
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии
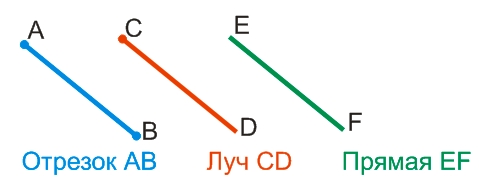
Отрезок, луч, прямая
Раздел математики, изучающий объемные фигуры и законы их измерения, называется геометрией.
Планиметрия изучает двумерные фигуры, расположенные на плоскости.
Простейшими фигурами планиметрии являются отрезок, луч и прямая.
Всё это прямые линии, главное отличие которых друг от друга заключается в следующем:
Провести «настоящую» прямую или луч невозможно, поэтому, ограничиваются построением отрезка, а чтобы различать отрезок, луч и прямую, ставят или не ставят точку в начале и конце отрезка:
Совпадающие прямые
Две прямые, расположенные в одной плоскости, могут либо пересекаться друг с другом (иметь одну общую точку), либо не пересекаться друг с другом (не иметь общих точек).
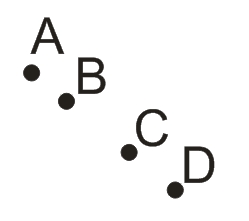
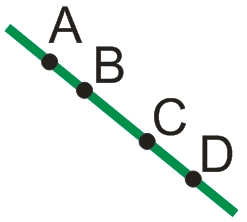
Возьмем произвольные четыре точки A, B, C, D, расположенные в одной плоскости и лежащие на одной прямой.
Очевидно, что вторая прямая наложится на первую. Говорят, что прямые AD и BC совместились или совпали.
Совпадающие прямые не являются ни пересекающимися, ни параллельными, поскольку имеют бесконечное множество общих точек. Все же, некоторые авторы совмещенные прямые рассматривают, как частный случай параллельных прямых, что, в общем-то, недалеко от истины.
Скрещивающиеся прямые
Две прямые, имеющие одну общую точку, называются скрещивающимися.
Перпендикулярными прямыми называются две скрещивающиеся прямые, при пересечении которых образуются четыре прямых угла.
Доказать это очень просто.
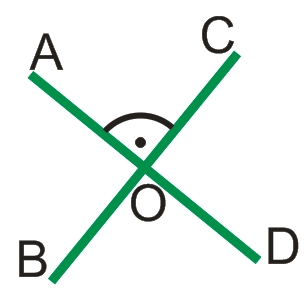
При пересечении двух прямых образуются 4 угла (см. рисунок выше): AOC, COD, DOB, BOA.
Если один из углов, например, АОС, равен 90°, то и смежный с ним угол COD также будет равен 90° (см. Что такое угол). Также будет прямым и другой смежный угол BOA.
Углы AOC и DOB также будут равны между собой, поскольку являются вертикальными углами.
Если же, какой-либо из углов (например, угол АОС) не является прямым, то прямыми не будут и смежные с ним углы COD и BOA. Поскольку, углы AOC и DOB являются вертикальными, то они равны между собой, а, т. к., угол АОС не равен 90°, то и угол DOB также не будет прямым.
Свойство перпендикулярных прямых: через любую точку плоскости можно провести тлько одну прямую, перпендикулярную данной прямой.
Параллельные прямые
Прямые будут параллельными, если они не имеют общих точек и при этом лежат в одной плоскости.
Аксиома параллельных прямых: через любую точку плоскости можно провести тлько одну прямую, параллельную данной прямой.
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Отрезок, луч, прямая
Раздел математики, изучающий объемные фигуры и законы их измерения, называется геометрией.
Планиметрия изучает двумерные фигуры, расположенные на плоскости.
Простейшими фигурами планиметрии являются отрезок, луч и прямая.
Всё это прямые линии, главное отличие которых друг от друга заключается в следующем:
Провести «настоящую» прямую или луч невозможно, поэтому, ограничиваются построением отрезка, а чтобы различать отрезок, луч и прямую, ставят или не ставят точку в начале и конце отрезка:
Совпадающие прямые
Две прямые, расположенные в одной плоскости, могут либо пересекаться друг с другом (иметь одну общую точку), либо не пересекаться друг с другом (не иметь общих точек).
Возьмем произвольные четыре точки A, B, C, D, расположенные в одной плоскости и лежащие на одной прямой.
Очевидно, что вторая прямая наложится на первую. Говорят, что прямые AD и BC совместились или совпали.
Совпадающие прямые не являются ни пересекающимися, ни параллельными, поскольку имеют бесконечное множество общих точек. Все же, некоторые авторы совмещенные прямые рассматривают, как частный случай параллельных прямых, что, в общем-то, недалеко от истины.
Скрещивающиеся прямые
Две прямые, имеющие одну общую точку, называются скрещивающимися.
Перпендикулярными прямыми называются две скрещивающиеся прямые, при пересечении которых образуются четыре прямых угла.
Доказать это очень просто.
При пересечении двух прямых образуются 4 угла (см. рисунок выше): AOC, COD, DOB, BOA.
Если один из углов, например, АОС, равен 90°, то и смежный с ним угол COD также будет равен 90° (см. Что такое угол). Также будет прямым и другой смежный угол BOA.
Углы AOC и DOB также будут равны между собой, поскольку являются вертикальными углами.
Если же, какой-либо из углов (например, угол АОС) не является прямым, то прямыми не будут и смежные с ним углы COD и BOA. Поскольку, углы AOC и DOB являются вертикальными, то они равны между собой, а, т. к., угол АОС не равен 90°, то и угол DOB также не будет прямым.
Свойство перпендикулярных прямых: через любую точку плоскости можно провести тлько одну прямую, перпендикулярную данной прямой.
Параллельные прямые
Прямые будут параллельными, если они не имеют общих точек и при этом лежат в одной плоскости.
Аксиома параллельных прямых: через любую точку плоскости можно провести тлько одну прямую, параллельную данной прямой.
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Как определяется понятие «отрезок» в геометрии
Содержание:
Для изображения прямых, лучей и отрезков применяют линейку. Отрезок на листике бумаги можно изобразить полностью, для луча и прямой – их фрагменты, ведь первый не имеет конца, только начало, вторая – бесконечна. Объясним, что такое отрезок в геометрии, чем отличается от иных фигур в евклидовом пространстве. Разберёмся с его свойствами.
Как выглядит отрезок
Обозначается двумя буквами – это название точек, лежащих в начале и конце. AB – концы геометрической фигуры, а расстояние между ними – длина фигуры, обозначается |AB|, измеряется преимущественно в сантиметрах.
Количество первых и вторых может быть любым.
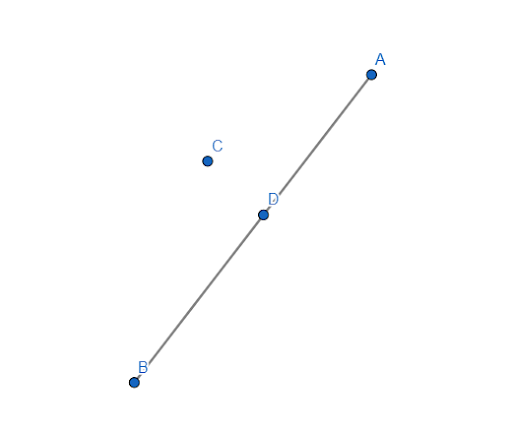
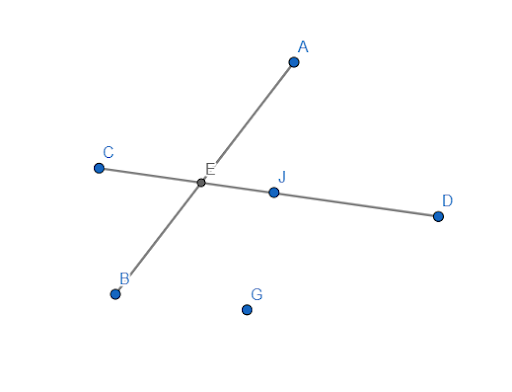
Различают следующие отрезки:
Выше показаны расположенные в одной точке пересекающиеся отрезки, имеющие общую точку – E. Два обрезка не могут иметь больше одной общей точки.
Разнообразие и измерение отрезков
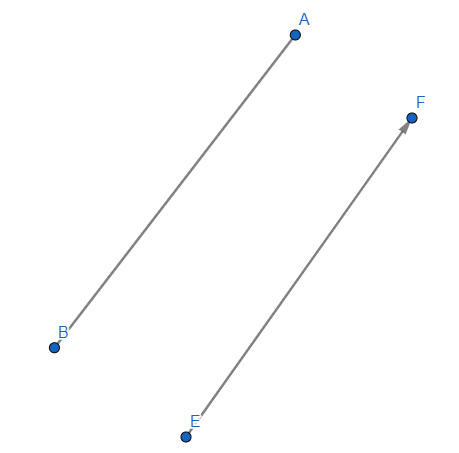
Геометрическая фигура AB тождественна или равная BA. Началом и концом может быть любая буква A или B, разницы нет. В случае с вектором фигура EF не равная FE.
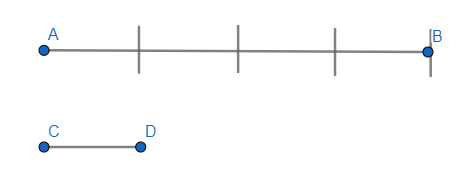
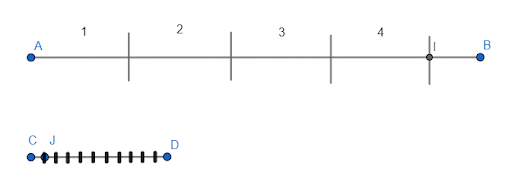
Измерение геометрических фигур основано на аксиоме Архимеда: дана пара отрезков разной длины, причём AB > CD. На AB можно отложить столько геометрических фигур CD, во сколько раз он меньше или короче AB.
CD. На AB можно отложить столько геометрических фигур CD, во сколько раз он меньше или короче AB.» src=»https://455811.selcdn.ru/BINGOCDN/default/moddocument/3023/e374aa7c42abc85c5922eca722ecfd2f1c4ee8aa.png» />
На практике их длина измеряется линейкой. Начальная точка совмещается с обозначением ноля на именительном приборе, точность которого равна одному миллиметру. Если конечная точка лежит между рисками на линейке, разницу в доли миллиметра не учитывают – значение округляют.
При измерении бывают следующие случаи (при условии, что AB > CD):
В подобных случаях обходятся избыточным и недостаточным измерениями. В первом – дробь округляют в меньшую сторону: если получается более 5,6, записывают 5,6; во втором – 5,7 см.