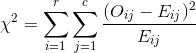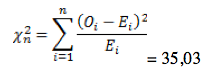Что такое хи квадрат в статистике
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
КРИТЕРИЙ ХИ-КВАДРАТ ПИРСОНА
– это непараметрический метод, который позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы. Выражаясь проще, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей).
1. История разработки критерия χ 2
Критерий хи-квадрат для анализа таблиц сопряженности был разработан и предложен в 1900 году английским математиком, статистиком, биологом и философом, основателем математической статистики и одним из основоположников биометрики Карлом Пирсоном (1857-1936).
2. Для чего используется критерий χ 2 Пирсона?
Критерий хи-квадрат может применяться при анализе таблиц сопряженности, содержащих сведения о частоте исходов в зависимости от наличия фактора риска. Например, четырехпольная таблица сопряженности выглядит следующим образом:
| Исход есть (1) | Исхода нет (0) | Всего | |
| Фактор риска есть (1) | A | B | A + B |
| Фактор риска отсутствует (0) | C | D | C + D |
| Всего | A + C | B + D | A + B + C + D |
Как заполнить такую таблицу сопряженности? Рассмотрим небольшой пример.
Заполняем исходными данными четырехпольную таблицу сопряженности:
| Артериальная гипертония есть (1) | Артериальной гипертонии нет (0) | Всего | |
| Курящие (1) | 40 | 30 | 70 |
| Некурящие (0) | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
Задача, которая ставится перед исследователем: имеются ли статистически значимые различия между частотой лиц с артериальным давлением среди курящих и некурящих? Ответить на этот вопрос можно, рассчитав критерий хи-квадрат Пирсона и сравнив получившееся значение с критическим.
3. Условия и ограничения применения критерия хи-квадрат Пирсона
4. Как рассчитать критерий хи-квадрат Пирсона?
| Исход есть (1) | Исхода нет (0) | Всего | |
| Фактор риска есть (1) | (A+B)*(A+C) / (A+B+C+D) | (A+B)*(B+D)/ (A+B+C+D) | A + B |
| Фактор риска отсутствует (0) | (C+D)*(A+C)/ (A+B+C+D) | (C+D)*(B+D)/ (A+B+C+D) | C + D |
| Всего | A + C | B + D | A+B+C+D |
Данный алгоритм применим как для четырехпольных, так и для многопольных таблиц.
5. Как интерпретировать значение критерия хи-квадрат Пирсона?
В том случае, если полученное значение критерия χ 2 больше критического, делаем вывод о наличии статистической взаимосвязи между изучаемым фактором риска и исходом при соответствующем уровне значимости.
6. Пример расчета критерия хи-квадрат Пирсона
Определим статистическую значимость влияния фактора курения на частоту случаев артериальной гипертонии по рассмотренной выше таблице:
χ 2 = (40-33.6) 2 /33.6 + (30-36.4) 2 /36.4 + (32-38.4) 2 /38.4 + (48-41.6) 2 /41.6 = 4.396.
О степенях свободы в статистике
В одном из предыдущих постов мы обсудили, пожалуй, центральное понятие в анализе данных и проверке гипотез — p-уровень значимости. Если мы не применяем байесовский подход, то именно значение p-value мы используем для принятия решения о том, достаточно ли у нас оснований отклонить нулевую гипотезу нашего исследования, т.е. гордо заявить миру, что у нас были получены статистически значимые различия.
Однако в большинстве статистических тестов, используемых для проверки гипотез, (например, t-тест, регрессионный анализ, дисперсионный анализ) рядом с p-value всегда соседствует такой показатель как число степеней свободы, он же degrees of freedom или просто сокращенно df, о нем мы сегодня и поговорим.
Степени свободы, о чем речь?
По моему мнению, понятие степеней свободы в статистике примечательно тем, что оно одновременно является и одним из самым важных в прикладной статистике (нам необходимо знать df для расчета p-value в озвученных тестах), но вместе с тем и одним из самых сложных для понимания определений для студентов-нематематиков, изучающих статистику.
Давайте рассмотрим пример небольшого статистического исследования, чтобы понять, зачем нам нужен показатель df, и в чем же с ним такая проблема. Допустим, мы решили проверить гипотезу о том, что средний рост жителей Санкт-Петербурга равняется 170 сантиметрам. Для этих целей мы набрали выборку из 16 человек и получили следующие результаты: средний рост по выборке оказался равен 173 при стандартном отклонении равном 4. Для проверки нашей гипотезы можно использовать одновыборочный t-критерий Стьюдента, позволяющий оценить, как сильно выборочное среднее отклонилось от предполагаемого среднего в генеральной совокупности в единицах стандартной ошибки:
Проведем необходимые расчеты и получим, что значение t-критерия равняется 3, отлично, осталось рассчитать p-value и задача решена. Однако, ознакомившись с особенностями t-распределения мы выясним, что его форма различается в зависимости от числа степеней свобод, рассчитываемых по формуле n-1, где n — это число наблюдений в выборке:

Сама по себе формула для расчета df выглядит весьма дружелюбной, подставили число наблюдений, вычли единичку и ответ готов: осталось рассчитать значение p-value, которое в нашем случае равняется 0.004.
Но почему n минус один?
Когда я впервые в жизни на лекции по статистике столкнулся с этой процедурой, у меня как и у многих студентов возник законный вопрос: а почему мы вычитаем единицу? Почему мы не вычитаем двойку, например? И почему мы вообще должны что-то вычитать из числа наблюдений в нашей выборке?
В учебнике я прочитал следующее объяснение, которое еще не раз в дальнейшем встречал в качестве ответа на данный вопрос:
“Допустим мы знаем, чему равняется выборочное среднее, тогда нам необходимо знать только n-1 элементов выборки, чтобы безошибочно определить чему равняется оставшейся n элемент”. Звучит разумно, однако такое объяснение скорее описывает некоторый математический прием, чем объясняет зачем нам понадобилось его применять при расчете t-критерия. Следующее распространенное объяснение звучит следующим образом: число степеней свободы — это разность числа наблюдений и числа оцененных параметров. При использовании одновыборочного t-критерия мы оценили один параметр — среднее значение в генеральной совокупности, используя n элементов выборки, значит df = n-1.
Однако ни первое, ни второе объяснение так и не помогает понять, зачем же именно нам потребовалось вычитать число оцененных параметров из числа наблюдений?
Причем тут распределение Хи-квадрат Пирсона?
Давайте двинемся чуть дальше в поисках ответа. Сначала обратимся к определению t-распределения, очевидно, что все ответы скрыты именно в нем. Итак случайная величина:
имеет t-распределение с df = ν, при условии, что Z – случайная величина со стандартным нормальным распределением N(0; 1), V – случайная величина с распределением Хи-квадрат, с ν числом степеней свобод, случайные величины Z и V независимы. Это уже серьезный шаг вперед, оказывается, за число степеней свободы ответственна случайная величина с распределением Хи-квадрат в знаменателе нашей формулы.
Давайте тогда изучим определение распределения Хи-квадрат. Распределение Хи-квадрат с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Кажется, мы уже совсем у цели, по крайней мере, теперь мы точно знаем, что такое число степеней свободы у распределения Хи-квадрат — это просто число независимых случайных величин с нормальным стандартным распределением, которые мы суммируем. Но все еще остается неясным, на каком этапе и зачем нам потребовалось вычитать единицу из этого значения?
Давайте рассмотрим небольшой пример, который наглядно иллюстрирует данную необходимость. Допустим, мы очень любим принимать важные жизненные решения, основываясь на результате подбрасывания монетки. Однако, последнее время, мы заподозрили нашу монетку в том, что у нее слишком часто выпадает орел. Чтобы попытаться отклонить гипотезу о том, что наша монетка на самом деле является честной, мы зафиксировали результаты 100 бросков и получили следующий результат: 60 раз выпал орел и только 40 раз выпала решка. Достаточно ли у нас оснований отклонить гипотезу о том, что монетка честная? В этом нам и поможет распределение Хи-квадрат Пирсона. Ведь если бы монетка была по настоящему честной, то ожидаемые, теоретические частоты выпадания орла и решки были бы одинаковыми, то есть 50 и 50. Легко рассчитать насколько сильно наблюдаемые частоты отклоняются от ожидаемых. Для этого рассчитаем расстояние Хи-квадрат Пирсона по, я думаю, знакомой большинству читателей формуле:
Где O — наблюдаемые, E — ожидаемые частоты.
Дело в том, что если верна нулевая гипотеза, то при многократном повторении нашего эксперимента распределение разности наблюдаемых и ожидаемых частот, деленная на корень из наблюдаемой частоты, может быть описано при помощи нормального стандартного распределения, а сумма квадратов k таких случайных нормальных величин это и будет по определению случайная величина, имеющая распределение Хи-квадрат.
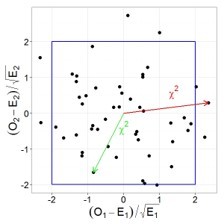
Давайте проиллюстрируем этот тезис графически, допустим у нас есть две случайные, независимые величины, имеющих стандартное нормальное распределение. Тогда их совместное распределение будет выглядеть следующим образом:
При этом квадрат расстояния от нуля до каждой точки это и будет случайная величина, имеющая распределение Хи-квадрат с двумя степенями свободы. Вспомнив теорему Пифагора, легко убедиться, что данное расстояние и есть сумма квадратов значений обеих величин.
Пришло время вычесть единичку!
Ну а теперь кульминация нашего повествования. Возвращаемся к нашей формуле расчета расстояния Хи-квадрат для проверки честности монетки, подставим имеющиеся данные в формулу и получим, что расстояние Хи-квадрат Пирсона равняется 4. Однако для определения p-value нам необходимо знать число степеней свободы, ведь форма распределения Хи-квадрат зависит от этого параметра, соответственно и критическое значение также будет различаться в зависимости от этого параметра.
Теперь самое интересное. Предположим, что мы решили многократно повторять 100 бросков, и каждый раз мы записывали наблюдаемые частоты орлов и решек, рассчитывали требуемые показатели (разность наблюдаемых и ожидаемых частот, деленная на корень из ожидаемой частоты) и как и в предыдущем примере наносили их на график.

Легко заметить, что теперь все точки выстраиваются в одну линию. Все дело в том, что в случае с монеткой наши слагаемые не являются независимыми, зная общее число бросков и число решек, мы всегда можем точно определить выпавшее число орлов и наоборот, поэтому мы не можем сказать, что два наших слагаемых — это две независимые случайные величины. Также вы можете убедиться, что все точки действительно всегда будут лежать на одной прямой: если у нас выпало 30 орлов, значит решек было 70, если орлов 70, то решек 30 и т.д. Таким образом, несмотря на то, что в нашей формуле было два слагаемых, для расчета p-value мы будем использовать распределение Хи-квадрат с одной степенью свободы! Вот мы наконец-то добрались до момента, когда нам потребовалось вычесть единицу. Если бы мы проверяли гипотезу о том, что наша игральная кость с шестью гранями является честной, то мы бы использовали распределение Хи-квадрат с 5 степенями свободы. Ведь зная общее число бросков и наблюдаемые частоты выпадения любых пяти граней, мы всегда можем точно определить, чему равняется число выпадений шестой грани.
Все становится на свои места
Теперь, вооружившись этими знаниями, вернемся к t-тесту:
в знаменателе у нас находится стандартная ошибка, которая представляет собой выборочное стандартное отклонение, делённое на корень из объёма выборки. В расчет стандартного отклонения входит сумма квадратов отклонений наблюдаемых значений от их среднего значения — то есть сумма нескольких случайных положительных величин. А мы уже знаем, что сумма квадратов n случайных величин может быть описана при помощи распределения хи-квадрат. Однако, несмотря на то, что у нас n слагаемых, у данного распределения будет n-1 степень свободы, так как зная выборочное среднее и n-1 элементов выборки, мы всегда можем точно задать последний элемент (отсюда и берется это объяснение про среднее и n-1 элементов необходимых для однозначного определения n элемента)! Получается, в знаменателе t-статистики у нас спрятано распределение хи-квадрат c n-1 степенями свободы, которое используется для описания распределения выборочного стандартного отклонения! Таким образом, степени свободы в t-распределении на самом деле берутся из распределения хи-квадрат, которое спрятано в формуле t-статистики. Кстати, важно отметить, что все приведенные выше рассуждения справедливы, если исследуемый признак имеет нормальное распределение в генеральной совокупности (или размер выборки достаточно велик), и если бы у нас действительно стояла цель проверить гипотезу о среднем значении роста в популяции, возможно, было бы разумнее использовать непараметрический критерий.
Схожая логика расчета числа степеней свободы сохраняется и при работе с другими тестами, например, в регрессионном или дисперсионном анализе, все дело в случайных величинах с распределением Хи-квадрат, которые присутствуют в формулах для расчета соответствующих критериев.
Таким образом, чтобы правильно интерпретировать результаты статистических исследований и разбираться, откуда возникают все показатели, которые мы получаем при использовании даже такого простого критерия как одновыборочный t-тест, любому исследователю необходимо хорошо понимать, какие математические идеи лежат в основании статистических методов.
Онлайн курсы по статистике: объясняем сложные темы простым языком
Стоит также отметить, что теоретические знания в области статистики будут определенно полезны не только тем, кто применяет статистику в академических целях, но и для тех, кто использует анализ данных в прикладных областях. Базовые знания в области статистики просто необходимы для освоения более сложных методов и подходов, которые используются в области машинного обучения и Data Mining. Таким образом, успешное прохождение наших курсов по введению в статистику — хороший старт в области анализа данных. Ну а если вы всерьез задумались о приобретении навыков работы с данными, думаем, вас может заинтересовать наша онлайн — программа по анализу данных, о которой мы подробнее писали здесь. Упомянутые курсы по статистике являются частью этой программы и позволят вам плавно погрузиться в мир статистики и машинного обучения. Однако пройти эти курсы без дедлайнов могут все желающие и вне контекста программы по анализу данных.
Хи-квадрат (χ 2 ) Пирсона: условия применения метода и интерпретация
Хи-квадрат Пирсона один из самых популярных статистических критериев для анализа качественных данных (номинальных, порядковых, ранговых), анализа частот. Однако, как и у каждого статистического критерия у хи-квадрата есть свои собственные правила применения метода, его интерпретации. Для того, чтобы Вы могли успешно овладеть этим ценнейшим статистическим инструментом сравнения статистических совокупностей по качественным данным предлагаем Вам ознакомиться с этой учебной статьей.
Как использовать хи-квадрат Пирсона?
Хи-квадрат используется прежде всего для анализа таблиц сопряженности (вид таблицы, которая учитывает совместное влияние фактора на исход, данные в таблице сопряженности должны быть представлены в виде частоты номинальных данных или интервалами, но не непрерывными количественными величинами). Стоит отметить, что при работе с сопряженными таблицами хи-квадрат часто является поддержкой для анализа влияния факторов риска с помощью расчета рисков (абсолютный и относительный риски) и отношение шансов.
Таблицы сопряженности могут принимать различные формы, простейшая таблица сопряженности выглядит следующим образом:
| Исход есть | Исхода нет | Всего | |
| Фактор риска есть | A | B | A+B |
| Фактора риска нет | C | D | C+D |
| Всего | A+C | B+D | A+B+C+D |
Как заполнить таблицу сопряженности? Обратимся к простому примеру:
Например, Вы хотите с помощью таблицы сопряженности и как следствия хи-квадрата Пирсона выяснить есть ли различия в частоте артериальной гипертонии в группах курящего и некурящего населения. Предполагается, что по остальным параметрам Ваши группы равномерны и превалирующим фактором риска развития артериальной гипертензии будет именно курение.
Для проведения исследования на основании ретроспективных данных (дизайн: случай-контроль) были отобраны две группы исследуемых — в первую вошли 70 человек, ежедневно выкуривающих не менее 1 пачки сигарет, во вторую группу вошли 80 некурящих такого же возраста, пола, и социального уровня (прочие систематически ошибки случайны).
В первой группе у 40 человек отмечалась артериальная гипертензия. Во второй — у 32 человек. Соответственно, референсное (нормальное) артериальное давление в группе «курильщиков» наблюдалось у 30 человек (70 — 40 = 30), а в группе «некурящих» нормальное АД наблюдалось у 48 (80 — 32 = 48).
Имея эти данные мы можем заполнить простейшую таблицу сопряженности:
| Повышенное АД | АД в пределах норма | Всего | |
| «Курильщики» | 40 | 30 | 70 |
| «Не курят» | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
АД- артериальное давление
Как видно из таблицы: каждая строка соответствует группе пациентов, которая подвергается влиянию фактора, каждый столбец, в свою очередь, обозначает частоту исходов в группе (к примеру: произошло/ не произошло, как в нашем примере).
Таблицы сопряженности служат удобным средством визуализации комбинации частот «фактор- исход» и субстратом для расчета хи-квадрата Пирсона, который в нашем случае сможет дать статистически точный ответ о случайности или не случайности наших находок.
Условия применения статистического критерия хи-квадрата Пирсона
бинарными (пол: мужской/женский, наличие или отсутствие заболевания)
порядковыми (степень артериальной гипертензии),
| Степень нарушения кровообращения | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | 49/13=3,77 | 16/12=1,33 | 9/5=1,80 |
| III | 81/34=2,38 | 144/32=4,50 | 9/14=0,64 |
| IV | 256/26=9,85 | 256/24=10,66 | 0/10*=0,10 |
| Всего | 16 | 16,49 | 2,54 |
как видно из данной таблицы одно из ожидаемых значений равно 0, в данном случае будет подставлена 1, корректнее применить точный критерий Фишера (см. Условия применения хи-квадрата Пирсона)
Четвертый этап
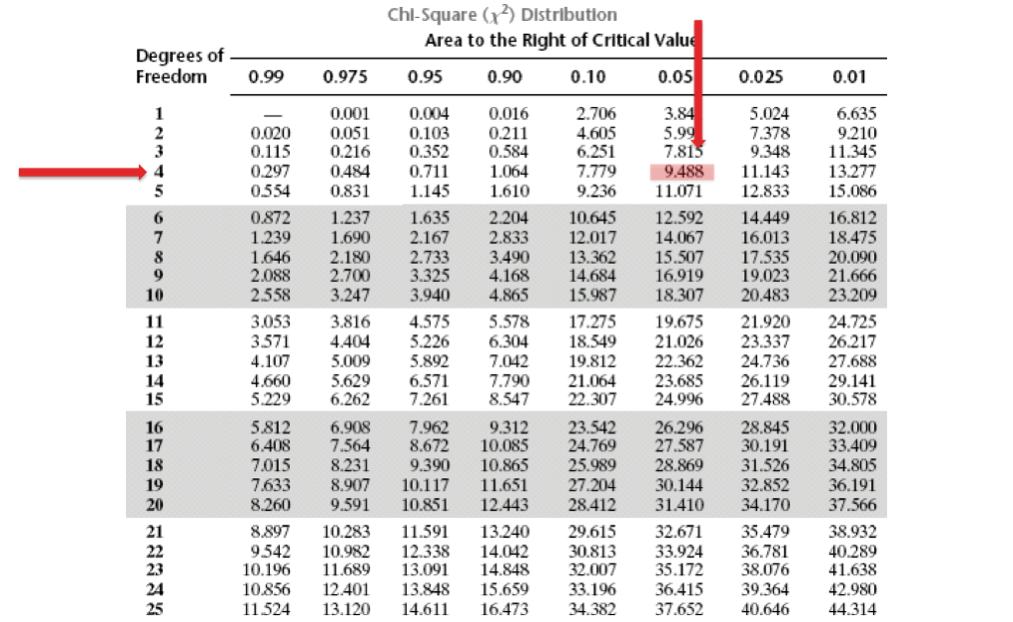
Необходимо соотнести полученное значение хи-квадрата с критическим значением хи-квадрата.Возникает вопрос, откуда брать критическое значение? Критическое значение хи-квадрата, как и для большинства, статистических критериев зависит от степени свободы и уровня достоверности (alpha), который Вы выбираете.В нашем случае, наше количество степеней свободы равно (3-1)*(3-1)=4, уровень значимости, который мы хотим соблюсти равен 0,05Обратимся к таблице критических значение хи-квадрата:
Инференциальная статистика: понимание гипотезы с использованием критерия хи-квадрат
Дата публикации Jul 11, 2019
Как инженер по науке о данных, крайне важно, чтобы набор выборочных данных, который вы выбираете из данных о населении, был надежным, чистым и хорошо проверенным на предмет его пригодности для построения моделей машинного обучения.
Так как ты это делаешь?Ну, у нас есть несколько статистических методов, таких как описательная статистика, где мы измеряем центральное значение данных, как они распределяются по среднему значению / медиане. Это нормально распределено или в разбросе данных есть перекос. Пожалуйста, обратитесь к моей предыдущей статье на том же для большей ясности.
Основы описательной статистики для аспирантов по науке о данных
Прикладная статистика фундаментальная для аспирантов Data Science
towardsdatascience.com
Первым делом мы визуализируем данные с использованием различных методов визуализации данных, чтобы на ранних этапах осознать любую асимметрию или несоответствие данных, чтобы идентифицировать любые виды взаимосвязей между переменными набора данных.
Данные имеют так много, чтобы сказать, и мы, инженер данных, даем им право высказывать и описывать себя, используя описательные статистические методы.
Но для того, чтобы делать какие-либо прогнозы или делать какие-то выводы, помимо данных, чтобы найти скрытую вероятность, мы полагаемся на методы логической статистики.
Инференциальная статистика касается выводов, основанных на отношениях, найденных в выборке, на отношениях в популяции. Инференциальная статистика помогает нам, например, решить, достаточно ли сильны различия между группами, которые мы видим в наших данных, чтобы поддержать нашу гипотезу о том, что групповые различия существуют в целом по всему населению.
Сегодня мы рассмотрим один из логически выведенных статистических механизмов для понимания концепции проверки гипотез с использованием популярного теста хи-квадрат.
Что такое тест хи-квадрат?
Это логический статистический тест, который работает с категориальными данными.
Тест хи-квадрат представляет собой статистический тест гипотезы, который предполагает (нулевая гипотеза), что наблюдаемые частоты для категориальной переменной соответствуют ожидаемым частотам для категориальной переменной. Тест вычисляет статистику, которая имеет распределение хи-квадрат, названное в честь греческой заглавной буквы Chi (X), произносится как «ки», как в кайте.
Мы пытаемся проверить вероятность тестовых данных (данных выборки), чтобы выяснить, является ли наблюдаемое распределение набора данных статистической случайностью (случайно) или нет.Статистика доброты соответствияв тесте хи-квадрат измеряет, насколько хорошо наблюдаемое распределение данных соответствует распределению, которое ожидается, если переменные являются независимыми.
Как работает Chi-Square?
Как правило, мы пытаемся установить связь между данной категориальной переменной в этом тесте. Хи-квадрат оценивает, являются ли данные переменные в наборе данных (выборке) независимыми, называемымиТест Независимости.Критерии хи-квадрат используются для проверки гипотез об одной или двух категориальных переменных иуместно, когда данные могут быть обобщены путем подсчета в таблице, Переменные могут иметь несколько категорий.
Тип теста хи-квадрат:
Для одной категориальной переменной мы выполняем
Проверка на соответствие критерия хи-квадрат начинается с предположения, что распределение переменной ведет себя определенным образом. Например, чтобы определить ежедневные кадровые потребности магазина розничной торговли, менеджер может пожелать узнать, существует ли равное количество покупателей каждый день недели.
Для двух категориальных переменных мы выполняем
Другой способ описать критерий хи-квадрат заключается в следующем:
Он проверяет нулевую гипотезу о том, что переменные являются независимыми.
Тест сравнивает наблюдаемые данные с моделью, которая распределяет данные в соответствии с ожиданием того, что переменные являются независимыми. В тех случаях, когда наблюдаемые данные не соответствуют модели, вероятность того, что переменные являются зависимыми, возрастает, что доказывает ошибочную гипотезу!
Гипотеза в хи-квадрат:
Прежде чем выполнять какие-либо дифференциальные статистические тесты, такие как Chi-Square, вы должны установить в качестве инженера данных.
Для одной категориальной переменной:
Для двух категориальных переменных:
Что такое распределение хи-квадрат?
распределение хи-квадрат(такжехи-квадратилиχ2-распределение) сКСтепени свободы это распределение суммы квадратовКнезависимые стандартные нормальные случайные величины.
Это одно из наиболее широко используемых распределений вероятностей в логической статистике, особенно при проверке гипотез или построении доверительных интервалов.
Основной причиной того, что распределение хи-квадрат широко используется при проверке гипотез, является его связь с нормальным распределением. Дополнительная причина, по которой широко используется распределение хи-квадрат, состоит в том, что он является членом класса тестов отношения правдоподобия (LRT). У LRT есть несколько желательных свойств; в частности, LRT обычно предоставляют высочайшую силу, чтобы отвергнуть нулевую гипотезу.
Степень свободы в распределении Чи в квадрате:
степени свободы(Д.Ф.илиd) скажу, сколько чисел в вашей сеткена самом деленезависимый. Для сетки хи-квадрат можно сказать, что степенью свободы является количество ячеек, которые необходимо заполнить до этого, учитывая итоги в полях, вы можете заполнить оставшуюся часть сетки, используя формулу.
Степени свободы для сетки хи-квадрат равны числу строк минус один раз, а число столбцов минус один: то есть (R-1) * (C-1).
Помнить!
По мере того как степень свободы (df) увеличивается, распределение хи-квадрат приближается к нормальному распределению
Статистика хи-квадрат:
Формула для статистики хи-квадрат, используемая в тесте хи-квадрат:
Индекс «сВот степени свободы. «ОЭто ваша наблюдаемая ценность иЕваше ожидаемое значение Символ суммирования означает, что вам придется выполнять вычисления для каждого отдельного элемента данных в вашем наборе данных.
E = (общее количество строк × общее количество столбцов) / размер выборки
Статистика хи-квадрат может использоваться только для чисел. Они не могут быть использованы для процентов, пропорций, средних или аналогичных статистических значений. Например, если у вас 10 процентов из 200 человек, вам нужно преобразовать это число (20), прежде чем вы сможете запустить тестовую статистику.
Тест хи-квадрат включает в себя вычисление метрики, называемой статистикой хи-квадрат, упомянутой выше, которая следует за распределением хи-квадрат.
Давайте рассмотрим пример, чтобы получить ясность по всем вышеупомянутым темам, связанным с хи-квадрат:
P-значение:
Нулевая гипотеза обеспечивает вероятностную структуру, с которой можно сравнивать наши данные. В частности, с помощью предложенной статистической модели нулевая гипотеза может быть представлена распределением вероятностей, называемымР-значение, который дает вероятность всех возможных результатов, если нулевая гипотеза верна;
Это вероятностное представление наших ожиданий при нулевой гипотезе.
Тест хи-квадрат, поясняемый примером:
Мы рассмотрим следующие важные шаги в нашем путешествии по тесту Chi_square для независимости двух переменных.
Проблема: эта проблема была получена изstarttrek
Опрос общественного мнения опросил простую случайную выборку из 1000 избирателей. Респонденты были классифицированы по полу (мужчина или женщина) и по избирательному предпочтению (республиканец, демократ или независимый). Результаты показаны в таблице непредвиденных расходов ниже.
Мы должны сделать вывод, есть ли гендерный разрыв? Значительно ли отличаются предпочтения мужчин при голосовании? Используйте уровень значимости 0,05.
Давайте попробуем решить эту проблему, используя критерий хи-квадрат, чтобы узнать значение P.
Вот тип теста, который мы будем использовать:
Тест хи-квадрат на независимость.
Итак, начнем с того, что сначала изложим нашу гипотезу.
Шаг 1: сформулируйте гипотезу:
Здесь нам нужно начать с установления нулевой гипотезы и контр-гипотезы (альтернативной гипотезы), как указано ниже.
Нулевая гипотеза:
Хо: Пол и избирательные предпочтения независимы.
Альтернативная гипотеза:
H1: Пол и предпочтения голосования не являются независимыми.
Шаг 2: Давайте создадим наш план анализа данных:
Здесь мы попытаемся выяснить значение P и сравнить его с уровнем значимости. Давайте возьмем стандарт и принялиуровень значимости должен быть 0,05.Учитывая пример данных в таблице выше, давайте попробуем использоватьТест хи-квадрат на независимость и вывести значение вероятности
Шаг 3: Давайте сделаем анализ образца:
Здесь мы проанализируем данные образца для вычисления
Все вышеперечисленные значения помогут нам найтиР-значение,
df = (2–1) * (3–1) = 1 * 2 = 2;
Расчет ожидаемой частоты:
Пусть Eij, представляет ожидаемые значения двух переменных, не зависящих друг от друга.
Eij = ih (итоговая строка X итоговая сумма в столбце) / итоговая сумма
Давайте вычислим ожидаемое значение для каждой данной строки и значения столбца, используя вышеупомянутую формулу. Позвольте мне снова скопировать изображение таблицы ниже, чтобы помочь вам сделать расчет легко,
Здесь общее значение строки 1 = 400, общее значение для column1 = 450, общий размер выборки = 1000,
E1,1 = (400 * 450) / 1000 = 180000/1000 = 180
Аналогично, давайте рассчитаем другие ожидаемые значения, как показано ниже,
E1,2 = (400 * 450) / 1000 = 180000/1000 = 180
E1,3 = (400 * 100) / 1000 = 40000/1000 = 40
E2,1 = (600 * 450) / 1000 = 270000/1000 = 270
E2,2 = (600 * 450) / 1000 = 270000/1000 = 270
E2,3 = (600 * 100) / 1000 = 60000/1000 = 60
Время для вычисления хи-квадратов для каждого вычисленного ожидаемого значения выше по формуле:
Расчет Chi-Sqaures:
Как уже обсуждалось выше, формула для расчета статистики хи-квадрат
Индекс «сВот степени свободы. «О”- ваше наблюдаемое значение (фактические значения приведены в таблице выше) иЕваше ожидаемое значение (которое мы только что рассчитали). Символ суммирования означает, что вам придется выполнять вычисления для каждого отдельного элемента данных в вашем наборе данных.
Используя приведенную выше формулу, наши значения хи-квадрат получаются такими, как указано ниже,
Χ² = (200–180) ² / 180 + (150–180) ² / 180 + (50–40) ² / 40 + (250–270) ² / 270 + (300–270) ² / 270 + (50– 60) ² / 60
Χ² = 400/180 + 900/180 + 100/40 + 400/270 + 900/270 + 100/60
Итак, наше окончательное значение статистики хи-квадрат,
Χ² = 2,22 + 5,00 + 2,50 + 1,48 + 3,33 + 1,67 = 16,2
Рассчитав значение хи-квадрат и степени свободы, мы просматриваем таблицу хи-квадрат, чтобы проверить, превышает ли статистика хи-квадрат 16,2 критическое значение для распределения хи-квадрат. Цель состоит в том, чтобы найтиЗначение P, которое является вероятностью того, что статистика хи-квадрат, имеющая 2 степени свободы, является более экстремальной, чем 16,2.
Как рассчитать P-значение?
Учитывая степень свободы = 2 и значение статистики хи-квадрат = 16,2, мы можем легко найти P-значение, используя это
Калькулятор хи-квадратссылку, просто введите статистическое значение хи-квадрат и степень свободы в качестве входных данных, а также сохраните свой уровень значимости как 0,05, вы найдете результат, как показано ниже,
Значение P =. 000304. Результат значим при р
Шаг 4: Интерпретация результата
A: Вывод из P-значения:
Так как мы получили P-значение 0,000304, мы можем интерпретировать результат, где это означает, что
Поскольку значение P (0,000304) меньше уровня значимости (0,05),
Таким образом, мы должны отклонить приведенное ниже
Нулевая гипотеза, который говорит, гНастройки ender и голосования независимы.
и принятьАльтернативная гипотеза:
Что говорит, гендерные и избирательные предпочтения не являются независимыми.
Отсюда можно сделать вывод, что
Существует связь между полом и предпочтениями при голосовании.
B: Интерпретация из таблицы хи-квадрат:
Поскольку критическое значение для альфа 0,05 (достоверность 95%) для df = 2 составляет 5,99, а наше статистическое значение хи-квадрат 16,3 намного больше 5,99, у нас есть достаточно доказательств, чтобы отвергнуть нашу гипотезу Null, которую мы рассмотрели выше.
Итак, мы принимаем альтернативную гипотезу:
Что говорит, гендерные и избирательные предпочтения не являются независимыми.
Отсюда мы заключаем, что
Существует связь между полом и предпочтениями при голосовании
Мы поймем, как выполнить тест Chi-Square с использованием ноутбука Python & Jupyter во второй части этой серии статей.Инференциальная статистика: проверка гипотез с использованием хи-квадрат и буду дальше исследовать
& также представит одну из ключевых тем: «Сила статистического теста »
Сила любого теста статистической значимости определяется как вероятность того, что он отвергнет ложную нулевую гипотезу.
Подводя итог этой части, с очень полезной инфографикой, которая поможет вам выбрать тип проверки гипотезы:
Поэтому выбирайте свои тестовые данные с умом и убедитесь, что вы правильно интерпретируете выборочные данные, чтобы вы могли продолжить разработку моделей ML с необходимой точностью и уверенностью.
Ваша способность быть эффективным исследователем данных в значительной степени станет реальностью только в том случае, если вы знаете, как анализировать данные выборки с минимальным отклонением. Чем больше вы обрабатываете данные с необходимой точностью и очищаете их на предварительной стадии EDA, тем более надежными и продуктивными будут ваши усилия по построению модели.