Что такое фактор гироскопической стабильности
Записки флинта
Копии некоторых моих постов на Российском оружейном портале
http://forum.guns.ru
Страницы
Saturday, February 28, 2004
Еще раз о формуле Зеленого Xолма или какая пуля нравится моему стволу
550 m/s). На более высоких скоростях, современные баллистики предложили заменить константу 150 на 180, и формула заработала опять.
В целом, в пределах одного калибра более длинная пуля означает что она более тяжелая. Т.е., в большинстве случев, даже без измерения длины пули можно примерно сказать по ее весу подходит она или нет вашему стволу. Предвижу массу возражений, что материалы, используемые для изготовления пуль и их компонентов варьируют по удельной плотности от пластмассы до свинца, поэтому прямой зависимости длины и веса нет и быт не может, но в целом такая тенденция просматривается.
Вот здесь сделаем Зарубку #1:
У каждого ствола есть ограничения (и главным образом по верхнему лимиту) по длине / весу пули.
Как я уже сказал выше, формула Гринхила является упрощенной моделью. Собственно формула гироскопической стабильности гораздо сложнее, и включает в себя несколько довольно трудно измеримых (скажем, в домашних условиях) факторов, как то Коэффициент опрокидывающего момента, Осевой момент инерции пули, Поперечный момент инерции пули, и т.д. Разбирать ее здесь не является моей задачей. А вот вывод из нее очень прост. Дабы пуля была стабильной, Гироскопический коэффициент должен быть больше единицы.
На shortmags.org нетак давно была опубликована модифициронанная «осовремененная» формула Гринхила. Некий гибрид между Гринхилом и формулой Гироскопический стабильности, в которой учитываются только диаметр, вес, длина и начальная скорость пули. Т.е. все, что вполне измеримо или уже известно.
Итак, для того, чтобы не словоблудить и не блуждать в теоретических потемках, я возьму для примера два наиболее часто ипользуемых нами калибра с наиболее типичными твистами.
Но для начала о критериях, которые мне дает «обновленная формула Гринхила».
SF = ((W*(20.62*(D^2.25))^2)/((T*(L^2.25))^2))/(1-(V/5705))
(Формула аккуратно выковыряна и Excel’овской таблички, которая была опубликована на ШортМаге.)
А теперь маленький шажок в сторону. А не отсюда ли у 223-го такая нестабильность и «отскакиваемость» от листиков да веточек в лесочке да среди кустиков.
Взгляните на секцию C таблицы: стоит перескочить на шаг нарезов 1:10 то все рассмотренные пули становятся стабильны.
Зарубка #3:
Серийной винтовке (twist 1:12) в 308-м подойдет практически любая пуля, кроме самых тяжелых (более 170 гран).
и
Зарубка #4:
Серийной винтовке (twist 1:12) в 223-м подойдет только 50-55 грановая пуля.
Спорно? Не согласны? Ну вот тогда независимый источник, который практически говорит тоже самое: http://benchrest.com/sst/shilentwist.html
Зарубка #5 и последняя.
Не спешите клясть боеприпас. Может, он сделан не для вашего ствола. Если нет табличных данных, распатроньте один. Промерьте длину пули. Диаметр вам известен, начальная скорость обычно на коробке, шаг нарезов в техпаспорте. Посчитайте.
Шаг нарезов
Начало
Нарезы, как известно, служат для того, чтобы, получив от них вращательное движение (угловую скорость), пуля приобрела гироскопическую устойчивость в полете. Устойчивость выражается через расчет фактора гироскопической стабильности (ФГС) или статической стабильности.
Гироскопическая стабильность пули
Фактор гироскопической стабильности должен быть больше единицы и выражается формулой:
,
Коэффициент опрокидывающего момента
Осевой момент инерции пули
Поперечный момент инерции пули
Плотность воздуха (зависит от температуры, давления и влажности)
линейная скорость пули (с учетом ветра)
угловая скорость пули
Калькулятор фактора гироскопической стабильности пули
Пуля M80 выпущена из ствола с шагом нарезов 1:12 под углом 32 градуса. При вылете из ствола коэффициент статической стабильности равен 1,35. Видно, как после 3000 метров наступает резкое снижение статической стабильности.
Формула Гринхила
шаг нарезов при заданной длине пули:
или при уже заданном шаге нарезов длина пули:
(150 * 0,308 2 ) / 1,35 = 10,54
Получаем приблизительно шаг нарезов 1:10,5 (10,54 дюймов на совершение полного оборота пули в стволе), что близко к используемому в винтовках калибра 30-06 шагу нарезов 1:10.
Если диаметр пули и ее длину брать в метрической системе, т.е в миллиметрах, константа НЕ МЕНЯЕТСЯ. Таким образом:
(150 * 7,82 2 ) / 34,29 = 267,51 мм
Калькулятор шага нарезов по формуле Гринхила
Исходные данные:
Константа (обычно 150) :
Диаметр пули, дюймов :
Результаты:
Шаг нарезов, дюймов :
Выводы
Вывод 1: Главную роль в стабилизации пули в играет ее длина, а не вес.
Вывод 2: Более длинные пули для стабилизации требуют более быстрых нарезов (меньшего шага нарезов)
Вывод 3: Шаг нарезов в изготавливаемоей винтовке выбирается по самой длинной (тяжелой) пуле, которая будет применяться в данном калибре.
Формула компании Sierra Bullets
0,06 * 2624 * 0,308 2 / 1,35 = 11, 063
Угловая скорость пули
Угловую скорость пули грубо можно оценить по формуле:
935/(12 * 0,0254) = 3 067,5 об/сек
Для вычисления угловой скорости можно воспользоваться калькулятором.
Типовой шаг нарезов в популярных калибрах
Рекомендуемые шаги нарезов в зависимости от калибра и веса пули
Ссылки
WinGyro программа для расчета фактора гироскопической стабильности
Calibers & Twists рекомендуемый шаг нарезов для разных калибров и весов пуль
Автор не несет никакой ответственности за любой вид ущерба, понесенного в результате использования присутствующей здесь информации. Автор оставляет на усмотрение читателя, применять полученные здесь сведения, или подвергнуть тщательной проверке в специализированных источниках.
Что такое фактор гироскопической стабильности
а с чем связан вопрос?
а с чем связан вопрос?
стабильность пули зависит от фактора гироскопической стабильности. фактически это некая инерционная составляющая приданная пуле, в следствии приложения ускорения и вращения в нарезах. с дистанцией падает, пуля становится нестабильной на траектории, максимально подвержена воздействиям из вне, может начать кувыркаться. начальный коэф.гироск.стабильности считается должен быть в промежутке 1.1-1.5 единиц, в зависимости от некоторых факторов. больше плохо, меньше тоже. насколько я понимаю на том самом «далеко», в районе мишени, не должен быть менее минимального значения. т.е. допустимо превышение ФГС в начале чтобы дотянуть до нужной дистанции, с возможной(но необъязательной) потерей кучности на дистанции до понижения ФГС до упомянутой вилки.
как то сумбурно, но вроде верно. если не прав поправте будет интересно.)
почти все правильно, НО:
скорость вращения пули падает намного медленнее, чем сама скорость пули и поэтому чем дальше по дистанции тем стабилизация пули только растет. И во многих случаях пуля на определенной дистанции становится перестабилизированной, что ведет к ухудшению кучности на бОльших дистанциях.
здесь все правильно, лучше если коэфициент 1.1-1.3
просто отличная скорость для 155 Бергера!
в идеале должно быть 1.1 чуть больше. вообще 155 пуля насколько я помню расчитана на 13-14 твист.
мне кажется, что перспективы очень хорошие, тем более, что куча в 0.2МОА просто отличная!
фишка в том, что 155 например у меня тоже хорошо летит с 11 твиста, но разогнать её до твоей скорости у меня вряд ли получится, твист не даст и вообще я заметил, что для 12 твиста 155 пуля очень подходит, но это не означает, что именно этот вариант самый идеальный.
мне кажется, что перспективы очень хорошие, тем более, что куча в 0.2МОА просто отличная!
фишка в том, что 155 например у меня тоже хорошо летит с 11 твиста, но разогнать её до твоей скорости у меня вряд ли получится, твист не даст и вообще я заметил, что для 12 твиста 155 пуля очень подходит, но это не означает, что именно этот вариант самый идеальный.
какие есть еще варианты? надо же в НН весной както бороться с 338 
скорость вращения пули падает намного медленнее, чем сама скорость пули и поэтому чем дальше по дистанции тем стабилизация пули только растет. И во многих случаях пуля на определенной дистанции становится перестабилизированной
честно говоря там много тяжелоучитываемых величин, форма, соотношение длинны пули к весу, фактор страгивания сердечника в оболочке и т.д. так называемый ВЛД фактор, удлиненные пули более устойчивы на высоких показателях ФГС, пример тому приведенный 155гран с 1.69. на начальный фгс влияет даже расположение ЦМ при прочих одинаковых величинах.
многие современные дальнобойные калибры при начальном фгс под 2 единицы отсутствием кучности на близких дистанциях не страдают.
вот было бы хорошо, чтобы Сеньер или ты как его ученик переубедил и всех нас и меня в том числе
так кто ж спорит, вот только бы сразу договориться, что понимать под понятием «кучность»? для одних 1МОА это просто супер, а другие 0.1 считают обычным результатом!
Указанные значения относятся к пуле при вылете из ствола.
В окошке пояснения к требованиям стабилизации.
Для необычных пуль требования к ФГС могут быть другими:
http://www.gsgroup.co.za/366260FN051.html
A value of 1.0 describes a bullet that is just barely stable. If the value drops below 1.0 a bullet is unstable; it yaws wildly. Accuracy is nonexistent.
It has been determined that a stability factor of 1.3 is the minimum level for reliable accuracy and performance.
Some authorities suggest that the stability factor should be no less that 1.5 for any application, including benchrest shooting.
Inside the barrel, the bullet is rotating about its centre of form, but as it exits the muzzle it starts rotating about its centre of gravity. If the centre of gravity of a poor quality bullet is offset from the central axis of symmetry on which the centre of form lies, then there can be a sudden sideways jump as the bullet exits the barrel. This jump can lead to a short term instability resulting in a large yaw angle and nutation which is not good for short range accuracy. The faster the rate of twist, the worse this short term instability is and the bigger the group size. So historically it has been important to keep the Stability Factor as low as possible. These days however, the quality of bullet manufacture is so good that using faster twists, resulting in higher Stability Factors than S = 1.5, is not really a problem.
By DANIEL LILJA
Lilja Precision Rifle Barrels, Inc.
PS
Немного о том, что формула Гринхилла устарела и нормальное значение ФГС=1.3-2.
Stability
Calculates the Miller stability factor.
This formula was derived by Don Miller and published in Precision Shooting. This formula is much better than the antiquated Greenhill’s formula. Stability value should be in the range of 1.3 to 2.0 to ensure bullet stability. Don Miller and Dave Brennan (editor of Precision Shooting) have also been kind enough to let me host his stability paper on my exterior ballistics bibliograpy page. The paper is titled A New Rule for Estimating Rifling Twist An Aid to Choosing Bullets and Rifles.
JBM Ballistics, LLC
. Значение ФГС должно находиться в диапазоне от 1,3 до 2,0 для обеспечения стабильности пули.
Важно понимать, что на 100м (при скорости =915-940мс) пуля еще может быть «не стабилизирована»(VLD в частности).
Пробуйте «прожигаться» на 100(2-3шт.) и пристреливаться на 300м, перед дальней дистанцией.
Продолжите пожалуйста мысль, что в результате получается на 100м и почему на 300м все приходит в норму? Сразу скажу, что я с вами согласен!
Сань, ты это что, капсюль поддувалом называешь?
«Подобранная» навеска на 100м, 5 выстрелов.
Вопрос, как прилетят на 1000yd пули собравшиеся в кучу на мишени ниже?
PS
Ответ Брайна Лица по поводу ФГС:
In other words, the label «under stabilized» that appears in the Loadbase calculation for SG’s above 1.3 and 1.4 is very conservative. The only way the bullet won’t actually be stable from a 1:12″ twist is if there’s more than 30% error in the Miller formula which is highly unlikely as 10% is likely to be the max error. If the calculated SG gets below 1.1, I’d start to worry that there might be a problem, but 1.3 and 1.4 is pretty safe.
To keep precession at the right level the first thing is to keep the stability factor from around 1.1 to 1.5 for your bullet of choice. Do not use the Greenhill formula to calculate the rate of twist you need, use of this formula is pretty much guaranteed to give you a twist that will stabilize the bullet. But, especially with secant ogive or VLD bullets, Greenhill’s formula can suggest twists that will overstabilize the bullet, preventing it tracking well at long range. The computation is not a trivial one, but there are computer programs available which will do this.
The next thing is to minimize in-bore yaw and keep good control of the launch ballistics. What am I talking about? If the bullet assumes some angle inside the barrel then you have in bore yaw. This is not good because on launch (exiting the muzzle) this yaw translates into precession and so increased drag. Secant ogive VLD bullets seem particularly susceptible to this problem and this may be overcome by loading the bullet out to such a length that the bullet touches the lands in the throat of the barrel. This keeps the bullet well centered on entry into the barrel. It is, of course, also important to load the bullet using an in line seating die or some method that keeps the bullet straight when loaded into the case.
You will also reduce your SD’s by using some form of bore lubricant, usually molybdenum disulfide in some form. The new ‘Black Diamond’ range of ammunition from Norma uses the NECO process of coating the bullets with a film of molybdenum disulfide, but you can probably do just as well by smearing a little molybdenum disulfide grease around the junction of the bullet and the case neck of your loaded rounds.
The rate of twist required to stabilize a bullet of a given caliber is directly proportional to its length. As bullets have become more streamlined for higher BC in any given weight category (as discussed above) they have gotten longer. Think about it a moment, the only way to increase the BC of a bullet at a given weight is to stretch the nose and maybe the boat tail to a more streamlined shape, thus lengthening it. That means that today’s bullets generally should use a slightly faster twist than the old ones.
I consider a 1:12″ to be the slowest desirable rate of twist for a Palma rifle today if one is not intent on shooting 155’s. The 1:13″ can shoot 175 and in some cases the 185 well, but it’s easier to get them shooting from a faster twist. The 1:12″ will shoot all of these perfectly well and in many cases the 190’s as well, although that’s not guaranteed.
Как летит пуля. Стабилизирующее вращение и сила Магнуса
Взаимодействие моментов при полете пули
Сила Магнуса и момент Магнуса
Двухплечевая модель рыскающего движения пули
Статически нестабильная пуля
Самовыравнивание пули вдоль набегающего потока воздуха
Выводы
Большинство людей полагает, что пули летят носиком вперед и остаются стабилизированными от дула до мишени, но это не обязательно так. На коротких дальностях большинство траекторий можно аппроксимировать до прямых линий, в то время как для больших дальностей необходимо принимать в расчет изгиб траекторий.
Большинство экспертов по стрелковому оружию принимают тот факт, что пули может болтать, когда они задевают какие-то объекты, или когда они пролетают промежуточные мишени. Тем не менее, как будет выяснено, некоторые физические условия должны быть выполнены для того, чтобы гарантировать стабильный полет, и пуля не будет стабилизироваться автоматически. Закручивание пули наделяет ее гироскопическими свойствами, которые очень важны – но не достаточны – для обеспечения стабильности пули.
Тем не менее, с точки зрения преподавания, движение вращающегося гироскопа является одним из наиболее сложных движений, с которым студенты-физики не дружат во время лекций по классической механике. Хотя движение гироскопов в целом может быть описано и полностью понято только путем тщательных математических расчетов, это вступление делает попытку описать элементы этого предмета посредством большого количества иллюстраций. Использование формул ограничено и предназначено только для тех, кто бы хотел их видеть Для объяснения некоторых основных физических терминов, используемых в статье, интересующийся читатель может обратиться к учебнику по элементарной физике.
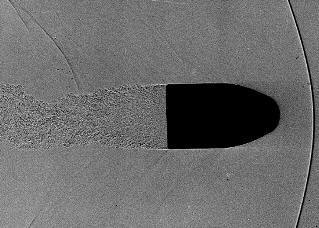
Отметьте изменение типа потока от ламинарного к турбулентному на каннелюре пули. Можно различить по крайней мере три ударные волны. Первая и наиболее интенсивная исходит от носика пули и называется конусом Маха. Вторая ударная волна начинается от расположения каннелюры, и третья ударная волна формируется за донцем пули. Кроме того, можно увидеть высоко турбулентный поток позади донца, который называется турбулентный след. Тип потока на поверхности пули изменяется от ламинарного пограничного слоя в переднем регионе пули, который характеризуется параллельными обтекающими линиями, до турбулентного потока, демонстрирующего завихрения, начинающиеся от каннелюры.
Теневая фотография демонстрирует поле обдувания пули, в основном состоящее из ламинарной и турбулентной областей. Поле обдувания в частности зависит от скорости, с которой движется пуля, формы пули и качества ее поверхности, как от наиболее важных факторов. Поле обдувания, очевидно, стремительно изменяется, когда скорость падает ниже скорости звука, которая составляет около 115 фт/с (340 м/с) для стандартных атмосферных условий.
9-мм оболочечная пистолетная пуля (9 mm Luger FMJ), летящая немного быстрее скорости звука.
Можно заметить серьезные отличия: конус Маха все еще присутствует, но он больше не прикреплен к носику пули, и угол открытия конуса увеличился. Турбулентный след все еще виден, но пограничный слой является ламинарным от носика до донца, на всем протяжении поверхности пули.
Математические формулы, посредством которых можно определить параметры поля обдувания (к примеру, давление и скорость поля обдувания в каждом положении) хорошо известны в математике, как уравнения Навье-Стокса. Тем не менее, данные уравнения и их действительные корни являются совершенно различными вещами. Даже с помощью мощных компьютеров до сих пор удалось найти всего лишь несколько применимых решений для некоторых специфических конфигураций. В виду таких математических ограничений баллистики по всему миру рассматривают движение пули в атмосфере, не учитывая специфических характеристик поля обдувания, и применяя упрощенную точку зрения: поле обдувания характеризуется силами и моментами, действующими на тело. В общем случае, эти силы и моменты должны быть определены экспериментально, что осуществляется в процессе стрелковых экспериментов и тестированием в аэродинамических трубах.
В общем случае, тело, движущееся через атмосферу, подвергается влиянию различных сил. Некоторые из этих сил являются силами массы, и прикладываются к СG (центру тяжести) тела и зависят от массы тела и ее распределения по телу. Вторая группа сил называется аэродинамическими силами. Эти силы происходят от взаимодействия поля обдувания с пулей и зависят от формы и качества поверхности тела. Некоторые аэродинамические силы зависят от рыскания, либо от вращения, либо от обоих из них.
Так как мы пытаемся изучать движение пуль на Земле, нам необходимо принимать во внимание ее вращение. Тем не менее, формулы Ньютона для движения справедливы только в инерциальной справочной системе координат – которая либо покоится, либо движется с постоянной скоростью. Поскольку мы считаем, что пуля движется в справочной системе координат, закрепленной на вращающейся Земле, нам приходится иметь дело с системой координат, движущейся с ускорением. Но мы можем компенсировать это – и все еще использовать формулы Ньютона – добавлением двух дополнительных сил.
Взаимодействие моментов при полете пули
Гироскопический эффект может быть описан и объяснен исходя из общих законов физики и может быть подтвержден математическими вычислениями. В данный момент мы просто должны принять то, что мы наблюдаем: ввиду гироскопического эффекта продольная ось пули движется в противоположном направлении от опрокидывающего момента, как показано стрелкой на рисунке.
В общем случае из-за влияния гироскопического эффекта, ось симметрии пули будет двигаться по поверхности конуса со скоростью, вектор которой будет направлен по оси конуса. Это движение часто называется прецессией. Тем не менее, более современные источники называют это медленной модой осцилляции. Опрокидывающий момент стремиться повернуть пулю вокруг оси, которая проходит через CG и которая перпендикулярна плоскости рыскания, плоскости, сформированной вектором скорости v и продольной осью пули. При отсутствии вращения угол рыскания d будет возрастать, и пуля начнет болтаться.
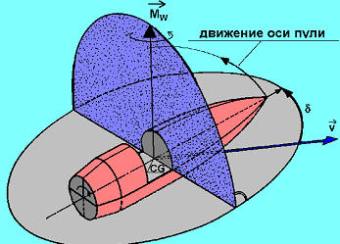
Если пуля обладает существенным вращением, скажем, если она вращается достаточно быстро вокруг оси своей симметрии, будет иметь место гироскопический эффект: продольная ось пули движется в направлении опрокидывающего момента, перпендикулярно к плоскости сопротивления. Тем не менее, эта ось смещается вместе с плоскостью сопротивления, которая затем поворачивается вокруг вектора скорости.
Чтобы еще больше все усложнить, скажем, что реальное движение стабилизируемой вращением пули еще более запутано. В дополнение к этому, к медленной осцилляции добавляется еще и быстрая осцилляция.
Поверхностное трение на поверхности пули замедляет ее вращательное движение. Момент затухания вращения (также момент затухания оборачивания) рассчитывается по приведенной выше формуле. Коэффициент затухания вращения зависит от геометрии пули и типа обтекания (ламинарное или турбулентное).
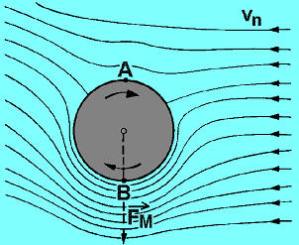
Сила Магнуса и момент Магнуса
В общем случае ветровая нагрузка будет являться доминирующей аэродинамической силой. Тем не менее, существует еще несколько более мелких сил, но нам бы хотелось упомянуть только силу Магнуса, которая, как оказывается, является очень важной для стабилизации пули.
Двухплечевая модель рыскающего движения пули
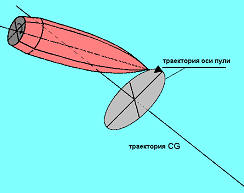
Теперь мы закончили обсуждать наиболее важные силы и аэродинамические моменты, влияющие на движение пули, но пока мы не видели, как выглядит результирующее движение пули. В данный момент нас не интересует сама по себе форма траектории (поступательное движение тела), но мы хотим сконцентрироваться на вращении вокруг ЦТ. Рыскающее движение пуль, стабилизируемых вращением, производимое суммой всех аэродинамических моментов, может быть смоделировано в виде суперпозиции быстрой и медленной мод осцилляции, и наиболее простым образом может быть объяснено и понято посредством двухплечевой модели.
Представьте себе, что вы смотрите на пулю сзади, как показано на рисунке. Простая двухплечевая модель адекватно описывает рыскающее движение пули, стабилизированной вращением, происходящее от взаимодействия всех аэродинамических моментов.
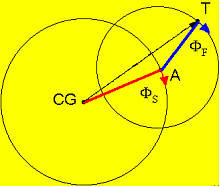
Рыскающее движение может быть осознано как суперпозиция быстрой и медленной осцилляций, часто называемых нутацией и прецессией. Представьте, что вы смотрите на пулю сзади. Плечо медленной моды от CG до A должно иметь точкой вращения CG и вращается с частотой медленной моды. Таким образом, А движется по окружности вокруг (красная окружность). Плечо быстрой моды от A до T, где T – носик пули, должно иметь точкой вращения точку А и вращаться с частотой быстрой моды. Таким образом, T вращается по окружности вокруг А. Расстояние от CG до T – это проекция продольной оси пули.
В соответствии с рисунком, представьте, что вы смотрите на пулю, летящую в сторону глаза наблюдателя. Тогда носик пули движется по спиралевидной (она еще называется геликоидной) траектории, как показано на рисунке, в то время, как CG остается закрепленным в центре окружности. Носик пули периодически возвращается назад, перпендикулярно к траектории. Если это происходит, угол рыскания становится минимальным.
Данный рисунок схематически показывает основное угловое движение пули, стабилизированной вращением, вблизи от дульного среза. Представьте, что CG пули закреплен в центре системы координат, и таким образом, пуля летит в направлении глаза наблюдателя. Тогда ее носик движется по спиралевидной траектории (как показано кривыми линиями) в направлении стрелок. На дульном срезе (t=0) угол рыскания может быть маленьким, но возрастать до максимального значения примерно в 1°, уменьшаясь затем снова почти до нуля.
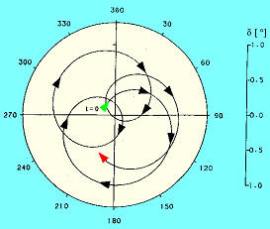
Отметьте, что величина успешных максимальных углов рыскания будет меньше, чем у их предшественников, так как пуля на рисунке предполагается динамически стабильной (максимальный угол рыскания уменьшается по мере того, как пуля продолжает продвигаться вперед).
Эта простая модель адекватно описывает рыскающее движение, если дополнительно принять, что частота быстрой моды превосходит частоту медленной моды, и длины плеч для медленной моды и быстрой моды для динамически стабилизированной пули постоянно укорачиваются.
ак как частота вращения w уменьшается намного медленнее, чем скорость vw, фактор гироскопической стабильности sg, как минимум вблизи от дульного среза, постоянно возрастает. Практический пример показан на рисунке 10 Этот рисунок демонстрирует фактор гироскопической стабильности для пули М80 калибра 7.62 x 51 НАТО, выстреленных под углом вылета 32° со скоростью 870 м/с из ствола с шагом нарезов в дульной части в 12 дюймов. Пуля M80 демонстрирует статическую стабильность на всем протяжении траектории полета, так как условие статической стабильности sg>1 сохраняется везде. Величина sg имеет минимальное значение 1.35 на дульном срезе.
Если, наоборот, пуля динамически нестабильна, угол рыскания увеличивается. Появление начального угла рыскания на дульном срезе вовсе не является индикатором нестабильности пули. В некоторых последних публикациях утверждения «пуля не стабилизирована» и «пуля показывает (большой) угол рыскания» используются как синонимы, что неверно. Наоборот, начальный угол рыскания на дульном срезе неизбежен и происходит из-за различных возмущений.
Равновесный угол рыскания (или рыскание покоя, также называемое равновесным рысканием) – это угол, на который отклоняется мгновенная ось прецессии от направления полета (см. рис). В результате влияния этого маленького наклона, возникает постоянный воздушный поток, который стремится отклонить пулю вправо. Таким образом, возникновение рыскания покоя является причиной, по которой пуля отклоняется вправо (для правосторонних нарезов) или влево (для левосторонних нарезов).
Поскольку мгновенное рыскание, получаемое на дульном срезе, у стабильной пули гасится, угол d становится равным рысканию покоя. Величина угла рыскания покоя обычно составляет лишь доли градуса около дульного среза, но может достигать существенных значений в верхней точке траектории, особенно для больших углов вылета.
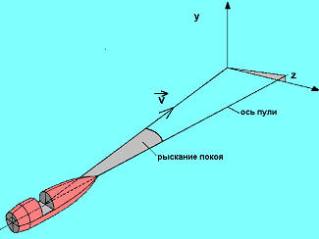
Возникновение рыскания покоя ответственно за боковой снос стабилизируемых вращением снарядов даже при отсутствии ветра. Зависящий от вращения боковой снос также называется деривацией. Также можно показать, что для правостороннего вращения рыскание покоя лежит справа от траектории. Таким образом, носик пули описывает розочку со средним смещением вправо, что приводит к боковому сносу вправо.
Статически нестабильная пуля
Возникает вопрос, в каких случаях эти нестабильности имеют существенный практический эффект. Если говорить о коротких дистанциях до нескольких тысяч калибров, динамическую нестабильность пули определить трудно, если, конечно, не применять очень сложную технику измерений. Если пуля сильно превышает эту дальность, угол рыскания достигает существенных значений, сопротивление возрастает и кучность падает. Скорее всего, вариации от выстрела к выстрелу будут ненормальными, а траектории станут непредсказуемыми.
Измерение скорости Доплеровским радаром для стандартной пули НАТО калибра 7.62×51, выстрелянной под углом 38.7° демонстрирует быструю потерю скорости вблизи дульного среза, но осциллирующую природу скорости для полетного времени, превышающего 14 секунд. Считается, что такая осцилляция скорости с частотой 1.0. 1.6 Гц может быть объяснена прецессионной нестабильностью, приводящей к конусообразному движению пули.
С первого взгляда все выглядит нормально. Скорость пули существенно уменьшается вблизи дульного среза, и после общего времени полета примерно в 30 секунд, пуля падает на дальности более 2,5 километров. Более пристальное изучение кривой зависимости скорости от времени, начиная с 14 секунд полета, четко демонстрирует осциллирующее поведение. Увеличенный сектор кривой зависимости скорости от времени показан на нижней иллюстрации рисунка.
Расчеты показывают, что частота колебания скорости возрастает от примерно одного оборота в секунду на 20 секундах полетного времени до почти двух оборотов в секунду на 28 секундах. Нет никаких сомнений в том, что измерения при помощи Доплеровского радара не являются ошибочными. С другой стороны, мы столкнулись не с аэродинамической силой, которая может быть ответственна за ускорение или замедление пули и вызывать осцилляции скорости. Это экспериментальное наблюдение можно объяснить динамической нестабильностью пули 7.62 х 51 НАТО на низких скоростях.
Из предыдущих рисунков мы узнали, что пуля калибра 7.62 х 51 НАТО статически и динамически стабильна вблизи дульного среза. Таким образом, рыскающее движение будет затухать, и после пролета определенной дистанции рыскание, за исключением небольшого рыскания покоя (деривации), практически окажется нулевым.
Когда скорость пули существенно снизится, и она начнет лететь на дозвуковой скорости, спектр обтекания сильно изменится. Это было подтверждено экспериментальными исследованиями BRL (смотри Выводы), и одним из последствий изменения спектра обтекания станет смещение центра давления для силы Магнуса. Для сверхзвуковой скорости эта точка располагается позади ЦТ, но перемещается вперед ЦТ на дозвуковых скоростях. Как было показано ранее (смотри рисунок 7 ), момент Магнуса становится сильным дестабилизирующим моментом, и как следствие, пуля становится динамически нестабильной.
Осцилляция на низких частотах, также называемая прецессией, больше не будет угасать и начинает медленно усиливаться. Тем не менее, пуля все еще имеет повышенную статическую стабильность, и, таким образом, гироскопический эффект продолжает иметь место. В конце концов, продольная ось пули смещается к поверхности конуса, в то время, как траектория является осью конуса. Так как эта осцилляция незатухающая, угол открытия конуса постоянно возрастает. Рисунок 26 схематически показывает конусообразное движение пули НАТО на ниспадающей ветви траектории.
Очевидно, что динамическая нестабильность пули НАТО оказывает заметное влияние на ее траекторию. По мере увеличения рыскания, скорость пули еще больше уменьшается, и дальность падает. Было отмечено, что для изучаемой партии пуль НАТО нестабильности были не воспроизводимы, и дальности, таким образом, даже при стрельбе на практически одинаковых дульных скоростях и при практически одинаковых углах вылета отличались существенно, по случайному закону. Стоит еще отметить, что расчеты внешней баллистики (смотри Выводы), основанные как на модели точечной массы, так и на модифицированной модели точечной массы не способны точно предсказать траекторию такой нестабильной пули.
Самовыравнивание пули вдоль набегающего потока воздуха
Пуля вылетает из ствола в неподвижную воздушную среду, т.е. воздух стоит на месте и бокового ветра нет. В горизонтальной плоскости все физические свойства гиростабилизированной пули имеют одинаковое значение относительно траектории ее полета. Углы рыскания влево и вправо одинаковы и компенсируют друг друга. Учитывая уменьшение этих углов по мере движения по траектории, мы можем принять, что пуля летит строго по линии вращения. Эта линия задана первоначально стрелком при выстреле.
Так она и будет лететь пока нет бокового ветра. Центр давления или максимального сопротивления набегающего потока воздуха находится впереди центра тяжести и располагается на линии полета. Пуля как бы закреплена в этом центре давления.
Далее появляется боковой ветер. Он осуществляет смещение вбок конуса ударной волны и через центр давления старается повернуть носик пули относительно центра тяжести. Дополнительно появляется набегающий поток воздуха внутри конуса ударной волны, который добавляет дополнительное отклонение по аналогии с подъемной силой крыла самолета на сверхзвуке.
Гироскоп, который представляет пуля, тут же старается вернуть ось своего вращения к ориентации, которая была до возмущения. Этот возврат происходит не центром давления, а центром тяжести. Пуля занимает первоначальное положение немного в стороне от прежней линии полета.
Мы знаем, что у гироскопа ось вращения уходит не по прямой от линии давления бокового воздуха, а и дополнительно отклоняется либо вверх, либо вниз, в зависимости от направления ветра. Это дополнительное отклонение так же приходит в ноль за счет гироскопического эффекта. В итоге пуля займет свою первоначальную ориентацию не только немного в стороне, а и выше, либо ниже.
Но ветер снова повторяет отклонение оси вращения пули и пуля снова компенсирует это отклонение гироскопическим эффектом. Так и идет борьба между боковым ветром и гироскопическим эффектом.
Как только ветер прекратится, этой борьбы не будет и пуля продолжит свой полет в той ориентации, которую обеспечивает гироскопический эффект.
Что касается набегающего потока воздуха внутри конуса ударной волны. При любом отклонении оси вращения, пуля перейдет, как вы сказали, в «мелкопериодические колебания». Набегающий поток будет не только с одной стороны, а и с противоположной. Сила его не одинакова слева и справа, поэтому в совокупности с основной силой отклонения ветром, появится некий малый угол.
Считается, что при боковом ветре в 20 миль в час центральная линия пули наклонится на угол 0,52 градуса относительно направления полета. Такой маленький и даже больший угол очень трудно заметить среди отклонений точек попадания пуль.
До настоящего времени не существует иного удобного метода, кроме эксперимента, с помощью которого можно предсказать динамическую нестабильность пули, особенно на дальних дистанциях. Некоторые очень сложные компьютеризованные процедуры (численные решения формул Навье-Стокса) для решения этих проблем только разрабатываются исследователями-баллистами.