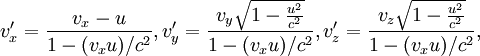что такое абсолютное движение твердого тела
Абсолютно твёрдое тело
Абсолю́тно твёрдое те́ло — второй опорный объект механики наряду с материальной точкой. Механика абсолютно твердого тела полностью сводима к механике материальных точек (с наложенными связями), но имеет собственное содержание (полезные понятия и соотношения, которые могут быть сформулированы в рамках модели абсолютно твердого тела), представляющее большой теоретический и практический интерес.
Существует несколько определений:
В трёхмерном пространстве и в случае отсутствия (других) связей абсолютно твёрдое тело обладает 6 степенями свободы: три поступательных и три вращательных. Исключение составляет двухатомная молекула или, на языке классической механики, твёрдый стержень нулевой толщины. Такая система имеет только две вращательных степени свободы.
Абсолютно твёрдых тел в природе не существует, однако в очень многих случаях, когда деформация тела мала и ей можно пренебречь, реальное тело может (приближенно) рассматриваться как абсолютно твёрдое тело без ущерба для задачи.
Содержание
Динамика абсолютно твердого тела
Динамика абсолютно твердого тела полностью определяется его полной массой, положением центра масс и тензором инерции (также, как динамика материальной точки — ее массой). (Конечно, имеется в виду, что заданы все внешние силы и внешние связи, которые, конечно, могут зависеть от формы тела или его частей и т.д.).
Другими словами, динамика абсолютно твердого тела при неизменных внешних силах зависит от распределения его масс только через полную массу, центр масс и тензор инерции, в остальном детали распределения масс абсолютно твердого тела никак не скажется на его движении [2] ; если как-то так перераспределить массы внутри абсолютно твердого тела, что не изменится центр масс и тензор инерции, движение твердого тела в заданных внешних силах не изменится (хотя при этом могут измениться и как правило изменятся внутренние напряжения в самом твердом теле!).
Частные определения
Абсолютно твёрдое тело на плоскости называется плоским ротатором. Он имеет 3 степени свободы: две поступательные и одну вращательную.
Абсолютно твёрдое тело с одной закреплённой точкой, неспособное вращаться и помещённое в поле тяжести, называется физическим маятником.
Абсолютно твёрдое тело с одной закреплённой точкой, но способное вращаться, называется волчком.
Абсолютное движение
В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух СО.
Обычно выбирают одну из СО за базовую («абсолютную»), другую называют «подвижной» и вводят следующие термины:
Также вводятся понятия соответствующих скоростей и ускорений. Например, переносная скорость — это скорость точки, обусловленная движением подвижной системы отсчёта относительно абсолютной. Другими словами, это скорость точки подвижной системы отсчёта, в данный момент времени совпадающей с материальной точкой.
Оказывается, что при получении связи ускорений в разных системах отсчёта возникает необходимость ввести ещё одно ускорение, обусловленное вращением подвижной системы отсчёта:
В дальнейшем рассмотрении, базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается.
Содержание
Классическая механика
Кинематика сложного движения точки
Скорость
Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть
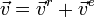
Ускорение
Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что координатные векторы подвижной системы координат также могут зависеть от времени.
Абсолютное ускорение точки равно геометрической сумме трёх ускорений — относительного, переносного и кориолисова, то есть
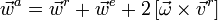
Кинематика сложного движения тела
Для твёрдого тела, когда все составные (то есть относительные и переносные) движения являются поступательными, абсолютное движение также является поступательным со скоростью, равной геометрической сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, например, у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геометрической сумме угловых скоростей составных движений. Если же составными движениями тела являются и поступательные, и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений.
Рассчитать взаимосвязь скоростей разных точек твёрдого тела в разных системах отсчёта можно с помощью комбинирования формулы сложения скоростей и формулы Эйлера для связи скоростей точек твёрдого тела. Связь ускорений находится простым дифференцированием полученного векторного равенства по времени.
Динамика сложного движения точки
При рассмотрении движения в неинерциальной СО нарушаются первые 2 закона Ньютона. Чтобы обеспечить формальное их выполнение, обычно вводятся дополнительные, фиктивные (не существующие на самом деле), силы инерции: центробежная сила и сила Кориолиса. Выражения для этих сил получаются из связи ускорений (предыдущий раздел).
Релятивистская механика
Скорость
При скоростях, близких к скорости света, преобразования Галилея не являются точно инвариантными и классическая формула сложения скоростей перестаёт выполняться. Вместо этого, инвариантными являются преобразования Лоренца, а связь скоростей в двух инерциальных СО получается следующей:
в предположении, что скорость 
Однако вводится величина — быстрота — которая аддитивна при переходе от одной СО к другой.
Неинерциальные СО
Связь скоростей и ускорений в системах отсчёта, движущихся друг относительно друга ускоренно, является значительно более сложной и определяется локальными свойствами пространства в рассматриваемых точках (зависит от производной тензора Римана).
Литература
См. также
Ссылки
Полезное
Смотреть что такое «Абсолютное движение» в других словарях:
абсолютное движение — сложное движение Движение точки по отношению к неподвижной системе отсчета. [http://sl3d.ru/o slovare.html] Тематики машиностроение в целом Синонимы сложное движение … Справочник технического переводчика
абсолютное движение — 3.1 абсолютное движение : Движение точек сооружения, определяемое как сумма переносного и относительного движений во время землетрясения. Источник: СП 14.13330.2014: Строительство в сейсмических районах 3.1 абсолютное движение: Движение точек… … Словарь-справочник терминов нормативно-технической документации
абсолютное движение — absoliutusis judėjimas statusas T sritis fizika atitikmenys: angl. absolute motion vok. absolute Bewegung, f rus. абсолютное движение, n pranc. mouvement absolu, m … Fizikos terminų žodynas
абсолютное движение точки или тела — Движение точки или тела по отношению к основной системе отсчета. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика Обобщающие … Справочник технического переводчика
абсолютное движение точки или тела — Движение точки или тела по отношению к основной системе отсчёта … Политехнический терминологический толковый словарь
Абсолютное пространство — в классической механике трёхмерное эвклидово пространство, в котором выполняется принцип относительности и преобразования Галилея. Термин введён Ньютоном (вместе с концепцией абсолютного времени) в «Математических началах натуральной философии».… … Википедия
Абсолютное, относительное и переносное ускорения — В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения когда материальная точка движется относительно какой либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом … Википедия
Абсолютное относительное и переносное ускорения — В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения когда материальная точка движется относительно какой либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом … Википедия
Абсолютное ускорение — В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения когда материальная точка движется относительно какой либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом … Википедия
движение — ▲ процесс ↑ перемещение < > неподвижный движение процесс перемещения. абсолютное движение. относительное движение. ↓ двинуться … Идеографический словарь русского языка
§ 7.1. Абсолютно твердое тело и виды его движения
При изучении кинематики мы говорили, что описать движение тела — это значит описать движение всех его точек. Иными словами, надо уметь находить координаты, скорость, ускорение, траектории всех точек тела. В общем случае это сложная задача, и мы не будем пытаться ее решать. Особенно она сложна, когда тела заметно деформируются в процессе движения.
Тело можно считать абсолютно твердым, если расстояния между двумя любыми точками тела неизменны. Иначе говоря, форма и размеры абсолютно твердого тела не изменяются при действии на него любых сил(1).
На самом деле таких тел нет. Это физическая модель. В тех случаях, когда деформации малы, можно реальные тела рассматривать как абсолютно твердые. Однако и движение твердого тела в общем случае сложно. Мы остановимся на двух, наиболее простых видах движения твердого тела: поступательном и вращательном.
Поступательное движение
Твердое тело движется поступательно, если любой отрезок прямой линии, жестко связанный с телом, все время перемещается параллельно самому себе.
При поступательном движении все точки тела совершают одинаковые перемещения, описывают одинаковые траектории, проходят одинаковые пути, имеют равные скорости и ускорения. Покажем это.
Пусть тело движется поступательно. Соединим две произвольные точки А и В тела отрезком прямой линии (рис. 7.1). Отрезок АВ должен оставаться параллельным самому себе. Расстояние АВ не изменяется, так как тело абсолютно твердое.
В процессе поступательного движения вектор 

Нетрудно заметить, что перемещения точек А и Б одинаковы и совершаются за одно и то же время. Следовательно, точки А и В имеют одинаковые скорости. Одинаковы у них и ускорения.
Совершенно очевидно, что для описания поступательного движения тела достаточно описать движение какой-либо одной его точки, так как все точки движутся одинаково. Лишь в этом движении можно говорить о скорости тела и ускорении тела. При любом другом движении тела его точки имеют различные скорости и ускорения, и термины «скорость тела» или «ускорение тела» теряют смысл.
Приблизительно поступательно движется ящик письменного стола, поршни двигателя автомобиля относительно цилиндров, вагоны на прямолинейном участке железной дороги, резец токарного станка относительно станины (рис. 7.2) и т. д.
Поступательными можно считать и движения, имеющие довольно сложный вид, например движение педали велосипеда или кабины «колеса обозрения» (рис. 7.3) в парках.
Вращательное движение
Вращательное движение вокруг неподвижной оси — еще один вид движения твердого тела.
Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, перпендикулярной плоскостям этих окружностей. Сама эта прямая есть ось вращения (MN на рисунке 7.4).
В технике такой вид движения встречается чрезвычайно часто: вращение валов двигателей и генераторов, колес современных скоростных электропоездов и деревенской телеги, турбин и пропеллеров самолетов и т. д. Вращается Земля вокруг своей оси.
Долгое время считалось, что в живых организмах устройств, подобных вращающемуся колесу, нет: «природа не создала колеса». Но исследования последних лет показали, что это не_так. У многих бактерий, например у кишечной палочки, имеется «мотор», вращающий жгутики. С помощью этих жгутиков бактерия перемещается в среде (рис. 7.5, а). Основание жгутика прикреплено к колесику (ротору) в форме кольца (рис. 7.5, б). Плоскость ротора параллельна другому кольцу, закрепленному в мембране клетки. Ротор вращается, делая до восьми оборотов в секунду. Механизм, приводящий ротор во вращение, остается пока во многом не ясным.
Кинематическое описание вращательного движения твердого тела
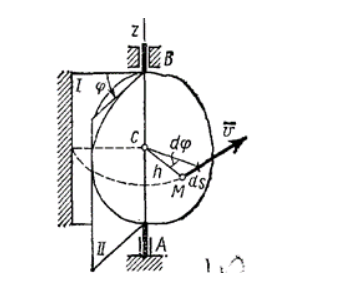
При вращении тела радиус rА окружности, описываемой точкой А этого тела (см. рис. 7.4), повернется за интервал времени Δt на некоторый угол φ. Легко видеть, что вследствие неизменности взаимного расположения точек тела на такой же угол φ повернутся за то же время и радиусы окружностей, описываемых любыми другими точками тела (см. рис. 7.4). Следовательно, этот угол φ можно считать величиной, характеризующей движение не только отдельной точки тела, но и вращательное движение всего тела в целом. Стало быть, для описания вращения твердого тела вокруг неподвижной оси достаточно лишь одной величины — переменной φ(t).
Этой единственной величиной (координатой) и может служить угол φ, на который поворачивается тело вокруг оси относительно некоторого своего положения, принятого за нулевое. Это положение задается осью О1Х на рисунке 7.4 (отрезки O2В, О3С параллельны О1Х).
В § 1.28 было рассмотрено движение точки по окружности. Были введены понятия угловой скорости ω и углового ускорения β. Так как при вращении твердого тела все его точки за одинаковые интервалы времени поворачиваются на одинаковые углы, то все формулы, описывающие движение точки по окружности, оказываются применимыми и для описания вращения твердого тела. Определения угловой скорости (1.28.2) и углового ускорения (1.28.6) могут быть отнесены к вращению твердого тела. Точно так же справедливы формулы (1.28.7) и (1.28.8) для описания движения твердого тела с постоянным угловым ускорением.
Связь между линейной и угловой скоростями (см. § 1.28) для каждой точки твердого тела дается формулой
где R — расстояние точки от оси вращения, т. е. радиус окружности, описываемой точкой вращающегося тела. Направлена линейная скорость по касательной к этой окружности. Различные точки твердого тела имеют разные линейные скорости при одной и той же угловой скорости.
Различные точки твердого тела имеют нормальные и тангенциальные ускорения, определяемые формулами (1.28.10) и (1.28.11):
Плоскопараллельное движение
Плоскопараллельным (или просто плоским) движением твердого тела называется такое движение, при котором каждая точка тела движется все время в одной плоскости. Причем все плоскости, в которых движутся точки, параллельны между собой. Типичный пример плоскопараллельного движения — качение цилиндра по плоскости. Плоскопараллельным является также движение колеса по прямому рельсу.
Напомним (в который раз!), что говорить о характере движения того или иного тела можно лишь по отношению к определенной системе отсчета. Так, в приведенных примерах в системе отсчета, связанной с рельсом (землей), движение цилиндpa или колеса является плоскопараллельным, а в системе отсчета, связанной с осью колеса (или цилиндра), — вращательным. Следовательно, скорость каждой точки колеса в системе отсчета, связаннои с землей (абсолютная скорость), согласно закону сложения скоростей равна векторной сумме линейной скорости вращательного движения (относительной скорости) и скорости поступательного движения оси (переносной скорости) (рис. 7.6):
Мгновенный центр вращения
Пусть тонкий диск катится по плоскости (рис. 7.7). Окружность можно рассматривать как правильный многоугольник со сколь угодно большим числом сторон.
Поэтому круг, изображенный на рисунке 7.7, можно мысленно заменить многоугольником (рис. 7.8). Но движение последнего состоит из ряда небольших поворотов: сначала вокруг точки С, затем вокруг точек С1, С2 и т. д. Поэтому движение диска тоже можно рассматривать как последовательность очень малых (бесконечно малых) поворотов вокруг точек С, C1 C2 и т. д.(2). Таким образом, в каждый момент времени диск вращается вокруг своей нижней точки С. Эта точка называется мгновенным центром вращения диска. В случае качения диска по плоскости можно говорить о мгновенной оси вращения. Этой осью является линия соприкосновения диска с плоскостью в данный момент времени.
Введение понятия мгновенного центра (мгновенной оси) вращения упрощает решение ряда задач. Например, зная, что центр диска имеет скорость и, можно найти скорость точки А (см. рис. 7.7). Действительно, так как диск вращается вокруг мгновенного центра С, то радиус вращения точки А равен АС, а радиус вращения точки О равен ОС. Но так как АС = 20С, то
Аналогично можно найти скорость любой точки этого диска.
Мы познакомились с наиболее простыми видами движения твердого тела: поступательным, вращательным, плоскопараллельным. В дальнейшем нам предстоит заняться динамикой твердого тела.
(1) В дальнейшем для краткости мы будем говорить просто о твердом теле.
(2) Разумеется, изобразить на рисунке многоугольник с бесконечным числом сторон невозможно.
Что такое абсолютное движение твердого тела
При любом ли движении тела можно использовать такую его модель, как материальная точка?
Какие модели тела ещё существуют?
Поступательное движение твёрдого тела.
Описание движения тела считается полным лишь тогда, когда известно, как движется каждая его точка.
Мы много внимания уделили описанию движения точки. Именно для точки вводятся понятия координат, скорости, ускорения, траектории. В общем случае задача описания движения тел является сложной. Особенно она сложна, если тела заметно деформируются в процессе движения. Проще описать движение тела, взаимное расположение частей которого не изменяется.
Тело, расстояние между любыми двумя точками которого остаётся постоянным при его движении, называется абсолютно твёрдым.
Абсолютно твёрдое тело — это одна из механических моделей, используемых при описании движения и взаимодействия тел.
На самом деле абсолютно твёрдых тел нет. Но в тех случаях, когда реальные тела при движении мало деформируются, их можно рассматривать как абсолютно твёрдые. Однако и движение абсолютно твёрдого тела в общем случае оказывается весьма сложным. Самое простое движение абсолютно твёрдых тел — поступательное.
Поступательным называется такое движение абсолютно твёрдого тела, при котором любой отрезок, соединяющий любые две точки тела, остаётся параллельным самому себе.
При поступательном движении все точки тела совершают одинаковые перемещения, описывают одинаковые траектории, проходят одинаковые пути, имеют в каждый момент времени равные скорости и ускорения. Покажем это.
Пусть тело движется поступательно (рис. 1.58). Соединим две его произвольные точки В и А отрезком. Расстояние |АВ| не изменяется, так как тело абсолютно твёрдое. При поступательном движении остаются постоянными модуль и направление вектора 

Согласно рисунку 1.58 перемещения точек А и В одинаковы и совершаются за одно и то же время. Очевидно, что любая точка твёрдого тела, например С, движется так же, как точки А и В.
Следовательно, точки А и В имеют одинаковые скорости и ускорения.
Совершенно очевидно, что для описания поступательного движения абсолютно твёрдого тела достаточно описать движение какой-либо одной его точки.
>Лишь при поступательном движении можно говорить о скорости и ускорении тела.
Примерно поступательно движутся ящик письменного стола, поршни двигателя автомобиля относительно цилиндров, вагоны на прямолинейном участке железной дороги, резец токарного станка относительно станины. Движение педали велосипеда или кабины колеса обозрения в парках (рис. 1.59, 1.60) — также примеры поступательного движения.
Для описания поступательного движения абсолютно твёрдого тела достаточно написать уравнение движения одной из его точек.
Вращательное движение абсолютно твёрдого тела.
Вращательное движение вокруг неподвижной оси — ещё один частный случай движения твёрдого тела.
В технике такой вид движения встречается очень часто: например, вращение валов двигателей и генераторов, турбин и пропеллеров самолётов.
Вращательным движением абсолютно твёрдого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения, при этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения.
Поступательное и вращательное движение
Движение твердого тела разделяют на виды:
Первые два из них – простейшие, а остальные представляют как комбинацию основных движений.
Поступательное криволинейное движение. Угол поворота тела
Поступательным называют движение твердого тела, при котором любая прямая, проведенная в нем, двигается, оставаясь параллельной своему начальному направлению.
Прямолинейное движение является поступательным, но не всякое поступательное будет прямолинейным. При наличии поступательного движения путь тела представляют в виде кривых линий.
Свойства поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые траектории и в каждый момент времени обладают одинаковыми по модулю и направлению значениями скорости и ускорения.
Следовательно, поступательное движение твердого тела определено движением любой его точки. Это сводится к задаче кинематики точки.
Понятие о скорости и ускорении тела имеют смысл только при наличии поступательного движения. В других случаях точки тела характеризуются разными скоростями и ускорениями.
Вращательное движение абсолютно твердого тела вокруг неподвижной оси – это движение всех точек тела, находящихся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывание окружностей, центры которых располагаются на этой оси.
При наличии такого вращения значения углов поворота радиус-вектора различных точек тела будут аналогичны.
Вращательное и поступательное движение. Формулы
| Поступательное | Вращательное |
| Равномерное | |
| s = υ · t | φ = ω · t |
| υ = c o n s t | ω = c o n s t |
| a = 0 | ε = 0 |
| Равнопеременное | |
| s = υ 0 t ± a t 2 2 | φ = ω 0 t ± ε · t 2 2 |
| υ = υ 0 ± a · t | ω = ω 0 ± ε · t |
| a = c o n s t | ε = c o n s t |
| Неравномерное | |
| s = f ( t ) | φ = f ( t ) |
| υ = d s d t | ω = d φ d t |
| a = d υ d t = d 2 s d t 2 | ε = d ω d t = d 2 φ d t 2 |
Задачи на вращательное движение
Решение
Решение