в какой точке находится изображение точки s в собирающей линзе

В какой точке находится изображение точки s в собирающей линзе

Могут ли линзы давать мнимые изображения предметов?

1) могут только собирающие линзы

2) могут только рассеивающие линзы

3) могут собирающие и рассеивающие линзы

4) никакие линзы не могут давать мнимые изображения.

Рассеивающие линзы всегда дают мнимое изображение. Собирающие линзы также могут давать мнимое изображение, для этого предмет должен быть приближен к линзе на расстояние меньшее, чем фокусное. Верно утверждение 3.

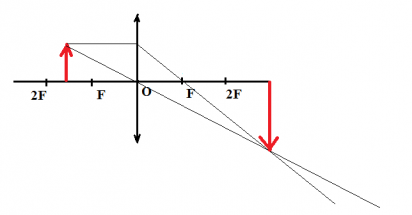
Ученик построил изображение A’B’ предмета AB в тонкой линзе.

Какие из лучей — 1, 2, 3, 4 — пройдут через точку B’?

Линза создает изображение источников света. Свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в одну точку (изображение), независимо от того, через какую часть линзы прошли лучи. Это означает, что все лучи, вышедшие из точки B, после преломления в линзе пройдут через точку B’.

Непонятно, почему все лучи должны пройти через точку B’.

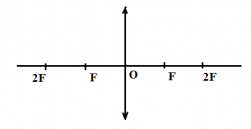
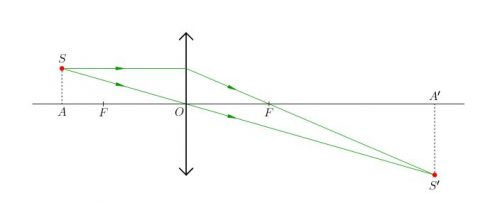
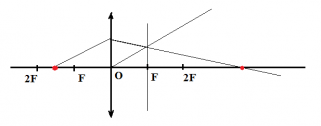
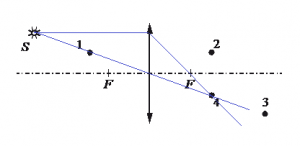
Какая из точек (1, 2, 3 или 4), показанных на рисунке, является изображением точки S в тонкой собирающей линзе с фокусным расстоянием F?

Построим изображение точки S в тонкой собирающей линзе. Луч, проходящий через оптический центр линзы, не меняет своего направления. Луч, направленный параллельно главной оптической оси, после преломления в линзе проходит через фокус.

Из рисунка видно, что изображением точки S является точка 2.

При расположении предмета на расстоянии 25 см от глаза на сетчатке получается его четкое изображение. Как должно измениться фокусное расстояние линзы-хрусталика при приближении предмета к глазу для получения четкого изображения этого предмета?

1) должно увеличиться

2) должно уменьшиться

3) не должно меняться

4) увеличится или уменьшится в зависимости от размера предмета

Оптическую систему глаза можно рассматривать как собирающую линзу с переменным фокусным расстоянием и неизменной «глубиной» (расстоянием от линзы до экрана), так как расстояние от хрусталика до сетчатки меняться не может. При приближении предмета для получения четкого изображения фокусное расстояние линзы-хрусталика должно уменьшиться. На примере формулы тонкой линзы: следовательно, если расстояние от предмета уменьшается, фокусное расстояние также уменьшается. Для глаза все аналогично.

Источник

Тонкие линзы. Построение изображений.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: построение изображений в линзах, формула тонкой линзы.

Правила хода лучей в тонких линзах, сформулированные в предыдущей теме, приводят нас к важнейшему утверждению.

Если в точке пересекаются сами преломлённые лучи, то изображение называется действительным. Оно может быть получено на экране, так как в точке концентрируется энергия световых лучей.

Теорема об изображении служит основой построения изображений в тонких линзах. Мы докажем эту теорему как для собирающей, так и для рассеивающей линзы.

Собирающая линза: действительное изображение точки.

Рис. 1. Случай a>f: действительное изображение точки S

Опустим перпендикуляры и на главную оптическую ось. Проведём также параллельно главной оптической оси, т. е. перпендикулярно линзе. Получим три пары подобных треугольников:

В результате имеем следующую цепочку равенств (номер формулы над знаком равенства указывает, из какой пары подобных треугольников данное равенство получено).

Отсюда находим искомое расстояние от точки до линзы:

Теорема об изображении в данном случае доказана.

Если источник не лежит на главной оптической оси, то в качестве удобных лучей годятся следующие:

Рис. 2. Построение изображения точки S, не лежащей на главной оптической оси

Рис. 3. Построение изображения точки S, лежащей на главной оптической оси

Посмотрим ещё раз на выражение ( 5 ). Его можно записать в несколько ином виде, более симпатичном и запоминающемся. Перенесём сначала единицу влево:

Теперь разделим обе части этого равенства на a:

Собирающая линза: действительное изображение предмета.

Рис. 4.

Из подобия треугольников и получим:

Формула (8) применяется во многих задачах, где фигурирует линейное увеличение линзы.

Рис. 5.a=2f: размер изображения равен размеру предмета

Рис. 6.a>2f: изображение действительное, перевёрнутое, уменьшенное

Рассмотрение первого случая f’ alt=’a>f’ /> нами полностью закончено. Переходим ко второму случаю. Он уже не будет столь объёмным.

Собирающая линза: мнимое изображение точки.

Снова обозначая через расстояние от до линзы, имеем соответствующую цепочку равенств (вы уже без труда в ней разберётесь):

Рис. 8. Построение изображения точки S, не лежащей на главной оптической оси

Рис. 9. Построение изображения точки S, лежащей на главной оптической оси

а затем делим обе части полученного равенства на a:

Собирающая линза: мнимое изображение предмета.

Учитывая это, мы легко строим изображение предмета, находящегося между линзой и фокальной плоскостью (рис. 10 ). Оно получается мнимым, прямым и увеличенным.

Рис. 10. : изображение мнимое, прямое, увеличенное

Собирающая линза: предмет в фокальной плоскости.

Рис. 11. a=f: изображение отсутствует

Соответственно, если предмет целиком расположен в фокальной плоскости, изображение этого предмета будет находиться на бесконечности (или, что то же самое, будет отсутствовать).

Итак, мы полностью рассмотрели построение изображений в собирающей линзе.

Рассеивающая линза: мнимое изображение точки.

К счастью, здесь нет такого разнообразия ситуаций, как для собирающей линзы. Характер изображения не зависит от того, на каком расстоянии предмет находится от рассеивающей линзы, так что случай тут будет один-единственный.

Рис. 12. Мнимое изображение точки S в рассеивающей линзе

Рис. 13. Построение изображения точки S, не лежащей на главной оптической оси

Если же точка лежит на главной оптической оси, то второй луч приходится брать произвольным (рис. 14 ).

Рис. 14. Построение изображения точки S, лежащей на главной оптической оси

Соотношение (13) даёт нам ещё один вариант формулы линзы. Сначала перепишем:

а потом разделим обе части полученного равенства на a:

Так выглядит формула линзы для рассеивающей линзы.

если соблюдать следующую договорённость о знаках:

— для мнимого изображения величина считается отрицательной;
— для рассеивающей линзы величина считается отрицательной.

Это очень удобно и охватывает все рассмотренные случаи.

Рассеивающая линза: мнимое изображение предмета.

Источник

Построение изображения в линзе

теория по физике 🧲 оптика

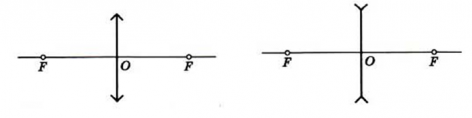
Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.

Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.

Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.

Способ построения изображений, а также

Вторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.

Построение изображения в собирающей линзе

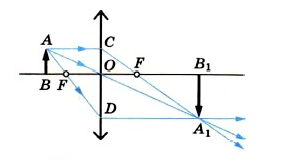
Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:

Два вида лучей при построении изображений в линзе

Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).

Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.

На пересечении двух лучей обозначаем точку А₁. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В₁. Изображение предмета при этом — А₁ В_1.

В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.

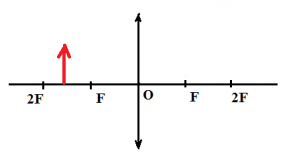
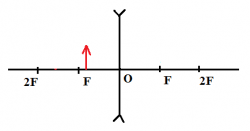
Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.

Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.

Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.

Частный случай — построение изображения точки

Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см. рисунок ниже). Так, изображению точки S соответствует точка S´.

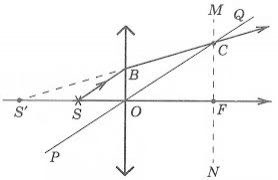
Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.

Пример №2. Построить изображение точки, расположенной на главной оптической оси.

Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.

Построение изображения в рассеивающей линзе

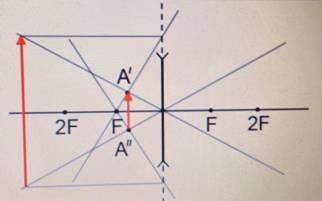
Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:

Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).

Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.

Пример №3. Построить изображение предмета в рассеивающей линзе.

Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.

Построение изображений в плоском зеркале

Плоское зеркало — это плоская поверхность, зеркально отражающая свет.

Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.

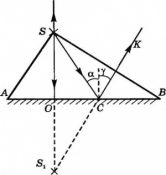
Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC. Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S₁, которое представляет собой точку пересечения продолжения отраженных лучей.

Таким образом, чтобы получить изображение в плоском зеркале, нужно:

Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.

Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S₁OC равны по стороне и двум углам. Следовательно SO = S₁O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.

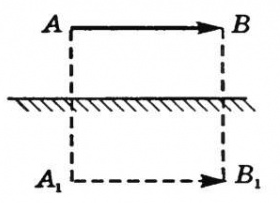
При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А₁В₁ соответствует предмету АВ.

Изображение и сам предмет всегда симметричны относительно зеркала.

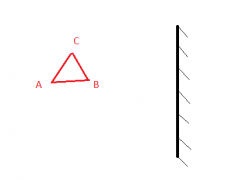
Пример №4. Построить изображение треугольника ABC в плоском зеркале.

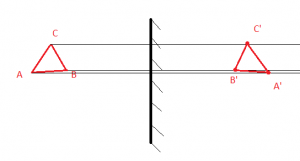
Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.

Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.

Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.

Источник

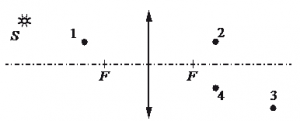
Задание EF18876

Какая точка является изображением точки S (см. рисунок), создаваемым тонкой собирающей линзой с фокусным расстоянием F?

Решение

Алгоритм решения

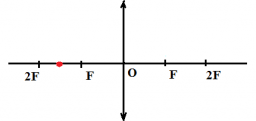
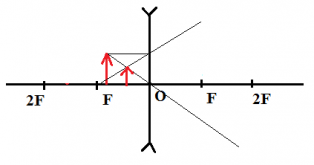
Решение

Построим изображение точки с учетом того, что линза собирающая. Для этого пустим из этой точки луч света, параллельный главной оптической оси. После прохождения через линзу луч преломится и пройдет через фокус. Затем пустим луч от этой точки через оптический центр линзы. Точка, в которой оба луча пересекутся, будет искомой. В данном случае это точка 4.

Добавить комментарий Отменить ответ

Похожие задания:

Дисперсия проявляется в следующих явлениях:
А. изменение видимого цвета белой.

Узкий пучок белого света после прохождения через стеклянную призму даёт на.

На поверхность тонкой прозрачной плёнки падает по нормали пучок белого света. В.

На две щели в экране слева падает плоская монохроматическая световая волна.

Точечные источники света S1 и S2 находятся близко друг от друга и создают на.

На плоскую непрозрачную пластину с узкими параллельными щелями падает по.

На рисунке приведены спектр поглощения неизвестного газа и спектры поглощения.

На рисунке приведены спектр поглощения разреженных атомарных паров неизвестного.

На рисунках А, Б и В приведены спектры излучения паров кальция Ca.

Свет падает на горизонтальное плоское зеркало. Угол между падающим и отражённым.

На рисунке показан ход двух лучей от точечного источника света А через тонкую.

Стеклянную линзу (показатель преломления стекла nстекла = 1,54), показанную на.

На рисунке показан ход лучей от точечного источника света А через тонкую линзу.

Предмет S отражается в плоском зеркале ab. На каком рисунке верно показано.

Как изменится период собственных электромагнитных колебаний в контуре (см.

В идеальном колебательном контуре (см. рисунок) напряжение между обкладками.

На рисунке приведён график зависимости силы тока i от времени t при свободных.

Катушка индуктивности подключена к источнику постоянного тока. Как изменится.

Энергия магнитного поля катушки с током равна 0,64 Дж. Индуктивность катушки.

В электромагнитной волне, распространяющейся со скоростью →v, происходят.

Какой объект, согласно классической электродинамике, не.

Выберите среди приведённых примеров электромагнитное излучение с минимальной.

Плоская рамка помещена в однородное магнитное поле, линии магнитной индукции.

Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5.

Проволочная рамка площадью 2×10–3 м2 вращается в однородном магнитном поле.

На рисунке запечатлён тот момент демонстрации по проверке правила Ленца, когда.

При вращении в однородном магнитном поле плоскости металлического кольца из.

Источник