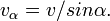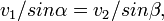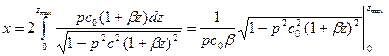в какой среде возникает рефрагированная волна

4.4. Рефрагированные волны

Ели мощности пластов в многослойном разрезе по сравнению с длиной волны очень малы, то можно говорить о непрерывном увеличении скорости с глубиной. Такие среды называются градиентными. В градиентных средах происходит искривление (рефракция) сейсмических лучей. Поэтому волны, распространяющиеся в градиентных средах, получили называние рефрагированных.

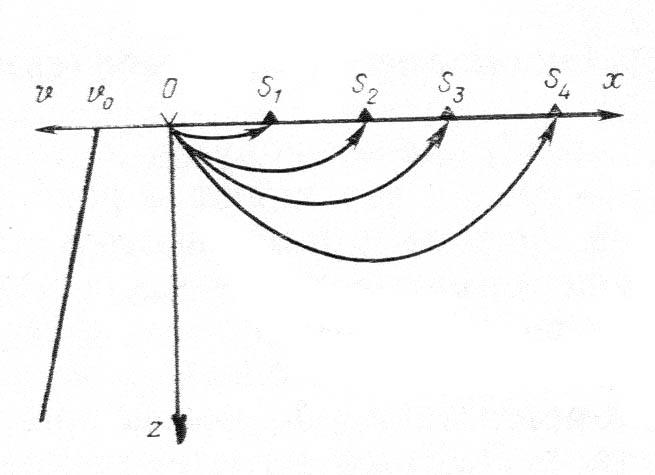
Наиболее важен для сейсморазведки случай, когда в среде скорость увеличивается с глубиной и лучи, вследствие этого, искривляются вогнутостью в сторону линии наблюдений. Тогда, рефрагированные волны, достигнув определенной глубины, распространяется в обратном направлении к линии наблюдений (рис. 4.5), где она регистрируется вместе с полезными отраженными и преломленными волнами. В сейсморазведке методом преломленных волн разработаны специальные методические приемы обнаружения рефрагированных волн.

Рис. 4.5. Ход лучей рефрагированных волн

4.5.Структура волнового поля

Совокупность колебаний, возникающих в геологической среде после воздействия источника, образует векторное волновое поле S(x,y,z,t), свойства и особенности которого определяются типом источника (взрывной или невзрывной), и распределением упругих свойств пород. Наблюдаемое на поверхности поле можно рассматривать, как результат сложения полей отдельных сейсмических волн, механизмы образования и пути распространения которых рассматривались нами ранее.

Вторичное поле источника. При распространении сейсмических волн вдали от источника в реальных геологических средах с большим числом границ всегда образуется множество вторичных волн.

Источник

Рефракция волн

Преломле́ние (рефра́кция) — явление изменения пути следования светового луча (или других волн), возникающее на границе раздела двух прозрачных (проницаемых для этих волн) сред или в толще среды с непрерывно изменяющимися свойствами. Преломление свойственно для многих видов излучения различной природы, например, электромагнитных и звуковых волн.

Тесно связано с преломлением такое явление, как отражение от границы прозрачных сред. В каком-то смысле это две стороны одного и того же явления. Так, например, явление полного внутреннего отражения связано с тем, что преломленной волны, которая бы удовлетворяла закону преломления для некоторых углов падения не находится, и волне приходится целиком отражаться.

Для каждого конкретного типа волн и сред имеются определенные соотношения, связывающие интенсивность падающей, преломленной и отраженной волны в зависимости от угла падения.

Физика явления

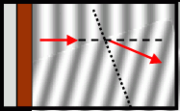
Преломление возникает, когда скорость движения волн в контактирующих средах различается (см. показатель преломления). В этом случае полное значение скорости волны должно быть разным по разные стороны границы раздела сред. Однако скорость движения гребня волны вдоль границы должна быть для обеих «половинок» волны одинаковой (ведь на границе не может быть резкого разрыва). 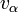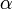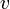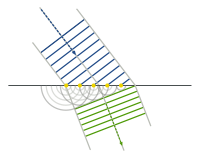Из геометрических соображений получается, что скорость движения гребня вдоль линии, наклоненной к направлению распространения волны под углом , выраженная через скорость гребня, измеренную в направлении распространения волны , будет

(Это ясно из того, что за то же время, пока волна пройдет в направлении своего распространения, то есть перпендикулярно гребню, расстояние, равное катету треугольника, вдоль наклонной линии она пройдет за это время расстояние, равное гипотенузе, а отношение этих расстояний, равное синусу угла, и даст отношение скоростей). См. также рисунки.

Тогда, записав для волны во второй среде то же самое и приравняв скорость вдоль границы раздела, получим

что эквивалентно закону Снелла, если учесть, что .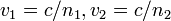

Для синусоидальной волны, характеризуемой частотой и волновым вектором, перпендикулярным (в изотропной среде, которая здесь и рассматривается) направлению распространения волны, такие же соображения дают понять, что составляющая волнового вектора, параллельная границе раздела, должна быть одинаковой до и после прохождения этой границы, что приводит к тому же выводу. (См. верхний рисунок).

Дополнительно интересно заметить, что волновой вектор фотона равен вектору его импульса, деленному на постоянную Планка, и это дает возможность дополнительной физической интерпретации закона преломления в терминах сохранения компоненты импульса вдоль границы.

Полное преломление

Источник

Годографы преломленных (головных) волн, их особенности для различных моделей сред. Рефрагированные волны

Особенности распространения упругих волн, энергия волн, эффекты ее поглощения, рассеяния и геометрического расхождения.

На процесс распр.упругих в-н влияют некоторые ф-ры среды: 1)геометрич.расхождение; 2)наличие в среде поглощения и рассеяния, 3)отражение энергии на акустич.жестких гран.;4)влияние неидентичности условий возбуждения и рассеяния;5) тонкая слоистость разреза;6) наложение волн-помех.

1)возб.произошло в т.О, пошел сферич.луч (внутри него энергия =const).сечение луча увелич. и кол-во эн.на единицу площади уменьш. О

2)среды не явл.абс.упр.(часть эн.тратится на трение м/у частицами),т.е. |А| уменьш.в соотв с коэфф.поглощ.

4)на разных участках проф.измен.усл.возб.и приема в-н. это надо учит.

6)из-за в-н –помех м.измен.частота и |А| колеб. МОГТ-способ подавл.этих в-н.

2. Слоистые среды, отражение и прохождение волн ч/з границу. Коэффициенты отражения.

В сейсморазведке принята модель слоистых сред. Поэтому нужно учит.,что при распростр.упругих волн, эти в-ны претерпевают отражение, преломление, рассеяние и др.процессы. при отражении в первую очередь происходит отраж.энергии на акустич.жестких гран.

Отражение энергии от акустически жестких границ несет в себе геологическую информацию о разрезе.

Типы волн, продольные, поперечные, поверхностные, обменные волны. Многоволновая сейсморазведка. Моделирование сейсм.волновых полей.

Типы волн

1.По характеру смещения частиц выделяют: поперечные (S) и продольные (Р).

Продольные волны ( деформация объема)- направление смещения частиц линейное и совпадает с направлением распр-я волны; распред. частиц сопровождается деформациями объёмного растяжения и сжатия.

Поперечные волны(деформация формы) – хар-ся линейными смещениями частиц в плоскости ^ плоскости смещения частиц; хар-ся деформациями сдвига и угловыми деформациями.

Поверхностные волны— распространяющиеся вдоль границы, не проникая глубоко в ½-пространство, распр.со скор.V_р

2.Типы волн по хар-ру пути в различных средах и по условиям генерации, по форме фронта в-н.

Прямые, проходящие, однократно- и многократно отраженные, преломленно-отраженные и отраженно-преломленные, дифрагированные, рефрагированные, зеркально-отраженные. Монотипные и обменные волны.

Волны-помехи: регулярные и нерегулярные (микросейсмы, фон помех).

4. Годографы однократно отраженных волн, их особенности для различных моделей сред. Многократные отраженные и дифрагированные волны, их годографы, способы подавления. Другие волны –помехи.

В слоист.среде крутизна год.меньше,чем в 1 случ. При криволин.отр.гран.на год.м.появл.точкиперегиба и разветвления.

Под дифракцией в широком смысле понимают всякое отклонение в распространении волн от законов отражения – преломления. Годограф дифр.в-ны имеет гиперболическую форму. Минимум гиперболы расположен над точкой отр. Годограф всегда касается годографа волны, подвергнувшейся дифракции, поскольку один из лучей всегда общий для обеих волн.

В-ны-помехи-все волны, кот. претерпели более 1отражения. Они засоряют сейсмозапись, мешают выделению и корреляции полезных волн. Для избавления от в-н-помех используют различные приемы при обработке сейсм.данных.

Осн.способ подавления в-помех – МОГТ (мет. многократн. перекрытий). МОГТ можно рассм. как интерференционную систему (суммирование сигналов из разных точек), ослабляются не только регулярные помехи, но и случайные,

Годографы преломленных (головных) волн, их особенности для различных моделей сред. Рефрагированные волны.

Самостоятельное движение фронта волны вдоль границы вызывает образование в среде вторичных волн, их называют головные волны.Распространение таких волн на значительном отрезке пути вдоль преломляющей границы и есть движение преломленных волн. Год.м.б. 2 видов: продольный,непродольный год.

Условия образования головных волн: 1) V2>V1 2) Падение под критическим углом.

Линейный годограф головной волны состоит из двух ветвей, разделенных мертвой зоной (зоной отсутствия головной волны). Знак кривизны годографа можно определить по направлению изменения угла наклона границы. Если преломляющая граница вогнутая, то годограф преломленной волны при этом обращен выпуклостью кверху и наоборот.

Рефрагированные волны —волны обладающие криволинейными лучами.

Годографы не выходят на поверхность.

6. Возбуждение упругих колебаний в сейсморазведке, преимущества и недостатки разных способов. Состав сейсморегистрирующего канала.

1)Осн.источник-взрывы(использование ВВ).Глубина закладки ВВ 5-25м. Явл.наиб.эффект.источником возб.упр.колеб.,колеб. получаются высокой частоты. Недостаток: высокая стоимость работ, нарушение экологии, ТБ.

2)Ударные источники(кувалда, падающ.груз, ГДУ(газо-динамич.установка)). Преимущества: не нарушает экологию. Недост.:слабые и низкочастотные источники.

3)Виброустановка.Высокочастотная. Широко используется.

Сейсморегистрирующая аппаратура явл.многоканальной,т.к. различные в-ны отл.по форме годографа. 120 каналов д.раб.2D, 8000 каналов-3D.

Невоспроизводимая запись.

Аналоговая магнит.запись

Цифровые системы

Телеметрические системы.

В них сигнал от СП попад в спец.полевой модуль, стоящий недалеко от СП, цифоровой модуль сейсм.сигн.преобраз.в цифровой вид.и по малопроводному кабелю передает в центральный регистр.блок, кот.создан на базе компа, где информация и записывается в памяти ЭВМ.

7. Линейные цифровые и телеметрические сейсморегистрирующие системы.

В наст.вр.регист.сейсмозаписи произв.на телеметрич.и цифровых сейсмостанциях(линейные и телеметрические). Линейные:120 каналов. В комплект помимо самой СС входит сумматор (д.сумм. слаб.записей),коррелятор(исп.с виброустан.). ФВК позв. выделять в виброграмме наличие свипа. Сейчас они произв.на базе Дельта-сигма технологий( ADST).

Телеметрические станции:

Суть: от СП сигнал поступает в модуль и преобраз.в цифр.вид, по связи перекачивается в ЦБ. Достоинства: отсутствие больш.тонкой косы, много каналов (1000 и более), что удобно для площадных работ, особенно с произвольн. сист.набл. Облад.большой диангностической способностью, контролир.раб.кажд.блока и запис.контрольн.ленту.

Источник

Годограф рефрагированной волны

Рефрагированная волна образуется при прохождении луча под границу раздела по криволинейной, выпуклой книзу траектории (рис. 62).

Найдем кривизну луча и определим ее связь с градиентом скорости. Из рис. 66 находим кривизну k (Облогина, 1968):

. (IX.32)

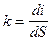
Изменение угла di ищем из закона преломления:

. (IX.33)

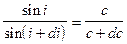
Так как угол i мал, то cos di » 1, sin di » di; и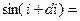
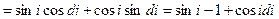
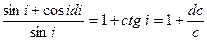
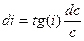
. Преобразуем (IX.33) пользуясь получен­ным выражением: . Отсюда

; . (IX.34)

Подставим (IX.34) в (IX.32):

. (IX.35)

, (IX.36)

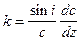
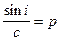
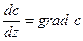
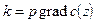
и, учитывая, что , окончательно получим выражение кривизны k

. (IX.37)

Формула (IX.37) связывает кривизну рефрагированного луча с градиентом скорости. Анализ ее показывает:

1) чем больше градиент скорости в геологической среде, тем больше кривизна луча k;

2) лучи имеют постоянную кривизну, т.е. дуги окружности, если скорость изменяется по линейному закону.

, (IX.38)

; . (IX.39)

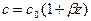
При c = const k = const;

3) луч обращен выпуклостью книзу, если grad c положителен, т.е. скорость с глубиной возрастает. Если же скорость убывает, то луч из выпуклого становится вогнутым, т.е. имеет точку перегиба;

4) чем больше угол i выхода луча из источника, тем больше его кривизна.

Найдем уравнение рефрагированного луча. Из рис. 66 находим:

; ; (IX.40)

. (IX.41)

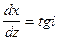
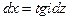
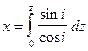
Введем согласно (IX.36) параметр p:

, (IX.42)

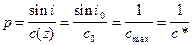
где с* – кажущаяся скорость. Следовательно,

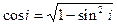
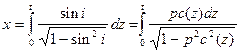
Так как , то выражение (IX.41) можно переписать в виде:

. (IX.44)

Мы получили интегральное уравнение рефрагированного луча. Найдем время пробега луча, т.е. годограф рефрагированной волны:

, (IX.45)

. (IX.46)

В итоге получаем интегральное выражение для годографа:

. (IX.47)

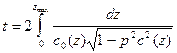
Теперь надо решить оба полученные уравнения (IX.43) и (IX.47). Зададимся линейным законом изменения скорости с глубиной (IX.38). Для решения уравнения (IX.44) воспользуемся простой формулой:

;

После подстановки пределов получим:

.

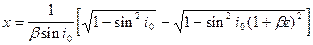
Возведем в квадрат обе части полученного уравнения и после простых преобразований получим:

. (IX.48)

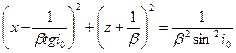
Это уравнение окружности с координатами центра , лежащего на прямой, параллельной оси x, и радиусом R, равным:

. (IX.49)

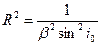
Таким образом, при линейном возрастании скорости с глубиной рефрагированная волна распространяется по окружности, центр которой расположен на прямой 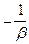, параллельной оси x (рис. 66).

Оценим z_max – глубину проникновения луча при данном законе изменения скорости:

, (IX.50)

. (IX.51)

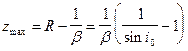
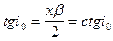
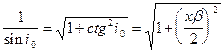
Из (IX.51) найдем: . Так как

,

то после подстановки полученного выражения в (IX.46) получим:

. (IX.52)

Формула (IX.52) позволяет определить глубину проникновения луча рефрагированной волны при линейном возрастании скорости с глубиной. Максимальное значение скорости на глубине z_max определим из выражения:

, (IX.53)

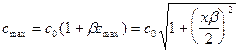
где градиент скорости b равен:

. (IX.54)

Анализируя полученное выражение для z_max, видим, что глубинность всегда зависит от базы наблюдения (взрыв-прибор), т.е. расстояния x. Чем больше это расстояние, тем глубже сейсмическая рефрагированная волна проходит в земную кору. Количественный анализ этой формулы и ее значение для понимания сейсмических данных ГСЗ по результатам исследования в океане будут даны в следующем параграфе.

Теперь обратимся к годографу рефрагированной волны (IX.47):

.

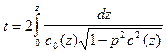
Решение этого интеграла требует громоздких вычислений, поэтому воспользуемся более простым методом, предложенным Т. И. Облогиной (1968). Кажущаяся скорость c* в точке выхода луча на земную поверхность равна истинной скорости в вершине луча, т.е.

. (IX.55)

. (IX.56)

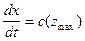
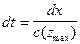
Отсюда уравнение годографа будет:

. (IX.57)

Поскольку c(z_max), как нам известно (IX.53), то:

. (IX.58)

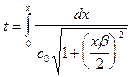
Это табличный интеграл вида 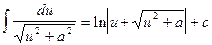. Поэтому

Но натуральный логарифм полученного выражения есть гиперболический синус:

.

. (IX.59)

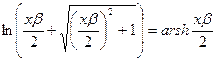
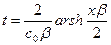
Это и есть уравнение годографа рефрагированной волны для линейного закона изменения скорости. Лучи и годографы показаны на рис. 62. При других законах изменения скорости с глубиной годограф будет иметь иной вид.

Каждую точку годографа рефрагированной волны можно рассматривать как точку вступления фиктивной головной волны. Поэтому О.К. Кондратьев предложил рассчитывать глубину проникновения луча по формуле

, (IX.60)

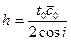
где t₀ – время, определяемое по годографу (рис. 66), с₀ – средняя скорость в толще, где проходит луч; .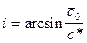

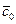
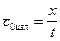
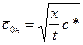
В соответствии с этим можно определить по точке излома годографа или по начальной точке ; или как среднее арифметическое из этих выражений:

. (IX.61)

Скорость в точке максимального проникновения луча, как было показано выше, равна кажущейся скорости, т.е.

. (IX.62)

Глубина H определяется по формуле:

. (IX.63)

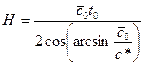
Более точная оценка глубины проникновения рефрагированной волны может быть проведена по формуле Гертглотца-Вихерта, преобразованной в 1934 г. С. В. Чибисовым для целей сейсморазведки:

. (IX.64)

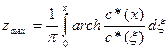
Дата добавления: 2015-06-27 ; просмотров: 1674 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник