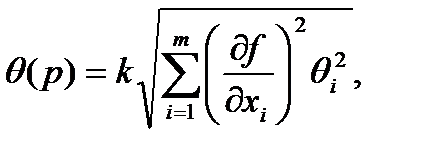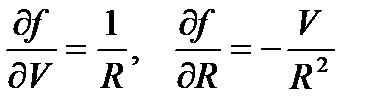в какой последовательности проводится оценивание неопределенности измерения
Аккредитация в Росаккредитации
форум для аккредитованных лабораторий
Неопределенность измерений
#1 Неопределенность измерений
Абсолютно точных измерений не существует. При проведении измерения его результат зависит от измерительной системы, методики измерения, квалификации оператора, внешних условий и других факторов. Так, если измерять одну и ту же величину несколько раз одним способом и в одинаковых условиях, то, как правило, полученные значения измеряемой величины всякий раз будут разными. Их среднее должно обеспечить значение оценки истинного значения величины, которая будет более достоверной, чем отдельное показание. Разброс показаний и их число дают некоторую информацию в отношении среднего значения как оценки истинного значения величины, однако, этого недостаточно. В руководстве по оценке неопределенности измерений (GUM) предложено выражать результат измерения как наилучшую оценку измеряемой величины вместе с соответствующей неопределенностью измерения. Неопределенность измерения можно представить через степень уверенности. Такая неопределенность будет отражать неполноту знания об измеряемой величине. Понятие «уверенности» очень важно, т. к. оно перемещает метрологию в сферу, где результат измерения должен рассматриваться и численно определяться в терминах вероятностей, которые выражают степень доверия. Неопределенность измерения — «неотрицательный параметр, характеризующий рассеяние значений, приписываемых измеряемой величине на основании используемой информации».
Таким образом, параметр этого распределения (также называемый — неопределенность) количественно характеризует точность результата измерений. Сходными для обоих подходов являются последовательности действий при оценивании характеристик погрешности и вычислении неопределенности измерений: Методы вычисления неопределенности, так же как и методы оценивания характеристик погрешности, заимствованы из математической статистики, однако при этом используются различные интерпретации закона распределения вероятностей случайных величин.
Из рассмотренных метрологических ситуаций можно предложить общее правило: результаты измерений в большинстве метрологических ситуаций характеризуются неопределенностью, а нормативы точности средств измерений, измерительных и контрольных процедур характеризуются погрешностью. Таким образом, понятия «неопределенность» и «погрешность» рекомендуется гармонично использовать без взаимного противопоставления и исключения одного из них.
Измерения выполняются ради оценки результата, сравнения его с нормативами и правила оценки результатов обуславливают требования к выполнению измерений.
Термины и определения
3.1 предельные значения, пределы поля допуска (limiting values, specification limits) L: Установленные значения параметра, представляющие собой верхнюю и/или нижнюю границы допустимых значений.
3.2 нижняя граница поля допуска (lower specification limit) L SL: Нижняя граница допустимых значений параметра.
3.3 верхняя граница поля допуска (upper specification limit) U SL:Верхняя граница допустимых значений параметра.
3.4 оценка соответствия (conformity test): Систематическая оценка соответствия продукции, процесса или услуги установленным требованиям посредством испытаний.
3.5 область допустимых значений (region of permissible values): Интервал или интервалы всех допустимых значений параметра.
Примечание – Если иначе не установлено, предельные значения считают принадлежащими области допустимых значений.
3.6 область недопустимых значений (region of non-permissible values): Интервал или интервалы всех недопустимых значений параметра.
Оценка соответствия — важный аспект управления качеством производства, метрологического надзора, проверки соответствия требованиям безопасности и санитарным нормам (например, по выбросам, уровню радиации, содержанию химических веществ и т. д.).
Измерение является неотъемлемой частью оценки соответствия, когда необходимо решить, соответствует ли выходная (измеряемая) величина установленному требованию. Для единственной величины такое требование обычно принимает вид границ, определяющих интервал допустимых значений величины. При отсутствии неопределенности полученное значение измеряемой величины, лежащее в пределах границ, считают соответствующим требованиям, в противном случае — несоответствующим. Наличие неопределенности измерения влияет на процедуру контроля и делает необходимым установление баланса рисков производителя и потребителя.
Возможные значения контролируемой величины представляют в виде распределения вероятностей. Можно рассчитать вероятность, с которой она соответствует установленным требованиям.
Хотя вышеизложенное справедливо для любых распределений вероятностей, в основном, целесообразно рассматривать случай нормального распределения как наиболее характерного для практики.
1.5. Оценка фактических уровней производственных физических факторов должна проводиться с учетом неопределенности измерений*(1).
*(1) ГОСТ Р 54500.1-2011/Руководство ИСО/МЭК 98-1:2009 “Неопределенность измерения. Введение в руководство по неопределенности измерения”, ГОСТ Р ИСО 10576-1-2006 “Руководство по оценке соответствия установленным требованиям.
Примечание: Приказом Росстандарта от 12 сентября 2017 г. N 1064-ст настоящий ГОСТ отменен с 1 сентября 2018 г. в связи с принятием и введением в действие ГОСТ 34100.1-2017/ISO/IEC Guide 98-1:2009 “Неопределенность измерения. Часть 1. Введение в руководства по выражению неопределенности измерения” для добровольного применения в РФ
СКО, характеризующее случайную погрешность Стандартная неопределенность, вычисленная по типу А
СКО, характеризующее неисключенную систематическую погрешность (погрешность СИ) Стандартная неопределенность, вычисленная по типу В
СКО, характеризующее суммарную погрешность Стандартная неопределенность, вычисленная по типу В
Доверительные границы погрешности Расширенная неопределенность
Метод исключения «промахов» по Q-критерию: (см также ГОСТ Р 8.736-2011)
Q=(X 1-X 2)/R
Наличие грубой погрешности доказано, если Q > Q (Р, n i).
Вычисление стандартной неопределённости измерений.
ПРИМЕЧАНИЕ: данный способ оценивания неопределённости измерений в терминологии ГОСТ Р 54500.3 является оцениванием по типу В. (настоящий ГОСТ отменен с 1 сентября 2018 г. в связи с принятием и введением в действие ГОСТ 34100.3-2017/ISO/IEC Guide 98-3:2008)
Среднеквадратическое отклонение: (синонимы: среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение; близкие термины: стандартное отклонение, стандартный разброс) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок.
где
Θ – граница НСП симметричного доверительного интервала (выражена как абсолютная погрешность СИ);
Θ+, Θ– верхняя и нижняя граница НСП для несимметричных доверительных интервалов, например, когда погрешность СИ несимметрична в положительную и отрицательную сторону (при измерении плотности потока энергии).
где
X i — результат i-ro наблюдения (единичного замера),
X̅ — среднее арифметическое значение оценки величины X (результат измерения),
n — количество наблюдений (замеров); для многократных измерений количество замеров должно быть не менее 4.
Встречаются ситуации, когда измерения проводятся с однократным наблюдением, и в этом случае стандартная неопределённость измерений оценивается только как Sθ., которая рассчитывается на основе погрешностей СИ.
Вычисление расширенной неопределённости измерений
Расширенная неопределенность измерений (U) определяется как суммарная стандартная неопределенность (u), умноженная на коэффициент охвата (k):
Коэффициент охвата для уровня доверия 95% для двухстороннего интервала охвата можно принять равным 2, а для одностороннего интервала охвата равным 1,64 при условии, что количество замеров будет не менее 11, что соответствует числу степеней свободы, равному 10 (ГОСТ 54500.3, п. 6.3.3, G6.6 (настоящий ГОСТ отменен с 1 сентября 2018 г. в связи с принятием и введением в действие ГОСТ 34100.3-2017/ISO/IEC Guide 98-3:2008). Таким образом, чем больше измерений в выборке, тем меньше ожидаемая неопределенность измерений.
Одно и двусторонний интервал охвата
Интервал охвата = интервал неопределённости (плохой перевод: ГОСТ Р 54500.3-2011/Руководство ИСО/МЭК 98-3:2008 (п. 6.2.2) Раньше использовались термины «одно — и двусторонние доверительные интервалы».
Если неопределённость оценивается по типу А, то интервал охвата=интервалу неопределённости
К чему ведет недостаточное количество измерений?
Коэффициент охвата для уровня доверия 95% для двухстороннего интервала охвата можно принять равным 2, а для одностороннего интервала охвата равным 1,64 при условии, что количество замеров будет не менее 11, что соответствует числу степеней свободы, равному 10 (ГОСТ 54500.3, п. 6.3.3, G6.6 ). Таким образом, чем больше измерений в выборке, тем меньше ожидаемая неопределенность измерений.
Аттестованная методика измерений (МИ) должна содержать значения установленной точности измерений в виде расширенной неопределённости.
При наличии установленного МИ диапазона расширенной неопределённости (U), приведенного в используемой аттестованной МИ, в протоколе измерений следует указывать ее значение, если целью исследования является оценка значения величины с некоторой точностью. Как правило, аттестованные МИ содержат установленные значения расширенной неопределённости измерений для двухстороннего охвата при уровне доверия 95%: ±U(95%), при этом используется коэффициент охвата (k), равный 2. В этом случае результат измерений приводится в протоколе как:
Представление результатов оценивания неопределенности
В какой последовательности проводится оценивание неопределенности измерения
ГОСТ Р ИСО 21748-2012
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
РУКОВОДСТВО ПО ИСПОЛЬЗОВАНИЮ ОЦЕНОК ПОВТОРЯЕМОСТИ, ВОСПРОИЗВОДИМОСТИ И ПРАВИЛЬНОСТИ ПРИ ОЦЕНКЕ НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЙ
Statistical methods. Guidance for the use of repeatability, reproducibility and trueness estimates in measurement uncertainty estimation
Дата введения 2013-12-01
Предисловие
1 ПОДГОТОВЛЕН Автономной некоммерческой организацией «Научно-исследовательский центр контроля и диагностики технических систем» (АНО «НИЦ КД») на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 29 ноября 2012 г. N 1419-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 21748:2010* «Руководство по использованию оценок повторяемости, воспроизводимости и правильности при оценке неопределенности измерений» (ISO 21748:2010 «Guidance for the use of repeatability, reproducibility and trueness estimates in measurement uncertainty estimation», IDT).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
6 ПЕРЕИЗДАНИЕ. Июль 2019 г.
Введение
Знание неопределенности результатов измерений крайне важно для принятия решений. Без количественных оценок неопределенности невозможно решить, превышают ли наблюдаемые отклонения результатов измерений заданную изменчивость, соответствуют ли объекты испытаний установленным требованиям. При отсутствии информации о неопределенности результатов измерений велика вероятность ошибочного принятия решений, которые могут привести к непредусмотренным расходам в процессе производства, неправильным судебным выводам, неблагоприятным последствиям для здоровья человека или неблагоприятным социальным последствиям.
ИСО/МЭК 17025:2005 «Общие требования к компетентности испытательных и поверочных лабораторий» (ISO/IEC 17025:2005 «General requirements for the competence of testing and calibration laboratories»).
ИСО 5725-2:1994 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерения» [ISO 5725-2:1994 «Accuracy (trueness and precision) of measurement methods and results. Part 2. Basic method for the determination of repeatability and reproducibility of a standard measurement method»]
Общий подход, используемый в настоящем стандарте, требует, чтобы:
— оценки повторяемости, воспроизводимости и правильности метода, полученные при межлабораторном исследовании в соответствии с ИСО 5725-2:1994, могли быть получены из опубликованной информации об использовании метода испытаний. Эти оценки позволяют получать внутрилабораторные и межлабораторные составляющие неопределенности, а также оценку неопределенности результатов, связанную с правильностью метода;
— лаборатория подтвердила на основе проверок присущих ей смещения и прецизионности, что качество выполнения ею метода испытаний соответствует установленным требованиям к методу испытаний, то есть подтвердила, что опубликованные данные о применении метода согласуются с результатами измерений и испытаний, полученными лабораторией;
— любые воздействия на результаты измерений, не охваченные межлабораторными исследованиями, были идентифицированы, а отклонения, вызванные этими воздействиями, определены количественно.
Оценку неопределенности определяют объединением оценок дисперсии, полученных в результате межлабораторных исследований в соответствии с GUM.
Для контроля полного понимания метода разброс результатов, полученных в межлабораторном исследовании, полезно сравнивать с оценками неопределенности измерений, полученными с использованием процедур GUM. Такие сравнения будут более эффективны при использовании последовательных оценок одного и того же параметра, полученных на основе данных совместных исследований.
Применяемый в настоящем стандарте международный стандарт разработан Техническим комитетом ИСО/ТС 69 «Применение статистических методов».
1 Область применения
В настоящем стандарте приведено руководство для:
— оценки неопределенности измерений на основе данных, полученных в результате исследований, проводимых в соответствии с ИСО 5725-2;
— сравнения результатов, полученных в межлабораторном исследовании, с оценками неопределенности измерений исследуемого параметра, полученными с использованием принципов переноса неопределенности (см. раздел 13).
В ИСО 5725-3 установлены дополнительные модели для анализа промежуточной прецизионности. Однако оценка неопределенности с использованием этих моделей не включена в настоящий стандарт, хотя этот общий подход может быть применен к более широкой группе моделей.
Настоящий стандарт применим во всех областях измерений и испытаний, когда должна быть определена неопределенность результатов.
В настоящем стандарте не приведено описание применения данных повторяемости в отсутствии данных воспроизводимости.
В настоящем стандарте использовано предположение, что признанные значимыми систематические воздействия устранены либо путем численной корректировки результатов, включенной в метод измерений, либо путем анализа и устранения причины воздействий.
В настоящем стандарте приведено общее руководство. Представленный подход к оценке неопределенности применим во многих случаях, однако возможно применение и других методов.
В общем случае информация, приведенная в настоящем стандарте, относительно результатов, методов и процессов измерений, относится также к результатам, методам и процессам испытаний.
2 Термины и определения
В настоящем стандарте применены термины по ИСО 5725-3, а также следующие термины с соответствующими определениями:
2.1 смещение (bias): Разность между математическим ожиданием результатов наблюдений испытаний и измерений и истинным значением.
1 Смещение представляет собой систематическую ошибку в противоположность случайной ошибке. Могут существовать одна или несколько причин, вызывающих систематическую ошибку. Большее систематическое отклонение от истинного значения соответствует большему значению смещения.
Применительно к измерениям под ошибкой следует понимать «погрешность».
3 На практике применяют вместо истинного значения принятое опорное значение.
[ИСО 3534-2:2006, определение 3.3.2]
2.2 суммарная стандартная неопределенность (combined standard uncertainty); : Стандартная неопределенность результата измерений, полученного через значения ряда других величин, равная положительному квадратному корню из суммы членов, представляющих собой дисперсии или ковариации этих величин, взятых с весами, соответствующими степени влияния этих величин на результат измерений.
[Руководство ИСО/МЭК 98-3:2008, определение 2.3.4]
2.3 коэффициент охвата (coverage factor); : Числовой коэффициент, на который умножают суммарную стандартную неопределенность при определении расширенной неопределенности.
[Руководство ИСО/МЭК 98-3:2008, определение 2.3.6]
2.4 расширенная неопределенность (expanded uncertainty); : Величина, определяющая интервал вокруг математического ожидания результатов измерений, охватывающий большую долю распределения значений, которые обоснованно могут быть приписаны измеряемой величине.
1 Долю распределения, охватывающую интервалом, характеризует вероятность охвата или уровень доверия интервала.
2 Чтобы связать определенный уровень доверия с интервалом расширенной неопределенности, необходимы предположения (в явной или неявной форме) о форме распределения вероятностей результатов измерений и их суммарной стандартной неопределенности. Уровень доверия, который соответствует этому интервалу, может соответствовать действительности только в той степени, в какой могут быть справедливы предположения.
3 В рекомендациях [20] расширенную неопределенность называют общей неопределенностью.
[Руководство ИСО/МЭК 98-3:2008, определение 2.3.5]
2.5 прецизионность (precision): Близость независимых результатов наблюдений, полученных при определенных принятых условиях.
1 Прецизионность зависит от распределения случайных ошибок и не связана ни с истинным, ни с заданным значениями.
2 Меру прецизионности обычно выражают в терминах изменчивости и вычисляют как стандартное отклонение результатов наблюдений (испытаний/измерений). Малой прецизионности соответствует большое стандартное отклонение.
3 Количественные меры прецизионности существенным образом зависят от принятых условий. Условия повторяемости и условия воспроизводимости являются примерами крайних вариантов принятых условий.
[ИСО 3534-2:2006, определение 3.3.4]
2.6 повторяемость (repeatability): Прецизионность в условиях повторяемости.
[ИСО 3534-2:2006, определение 3.3.5]
2.7 условия повторяемости (repeatability conditions): Условия наблюдений, при которых независимые результаты наблюдений (испытаний/измерений) получают одним и тем же методом на идентичных объектах наблюдений, в одной и той же лаборатории, с применением одних и тех же средств испытаний/измерений, одним и тем же оператором, с использованием одного и того же оборудования в течение короткого интервала времени.
— процедур измерений или испытаний;
— измерительного и испытательного оборудования, используемых в одних и тех же условиях;
Методика оценивания результата измерений и его неопределенности
Оценивание результата измерений и его неопределенности проводится в следующей последовательности:
-составление уравнения измерений;
-оценка входных величин и их стандартных отклонений (неопределенностей);
-оценка измеряемой (выходной) величины и ее неопределенности;
— составление бюджета неопределенности;
-оценка расширенной неопределенности результата измерений;
-представление результата измерений.
Рассмотрим эти составляющие подробнее.

Пусть имеются результаты ni измерений входной величины Xi, где i = 1…m. Как известно, при нормальном распределении наилучшей оценкой этой величины является среднее арифметическое
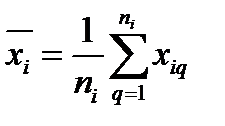
Стандартную неопределенность типа А определяют как среднеквадратическое отклонение по формуле:

Для вычисления стандартной неопределенности по типу В используют:
-данные о предыдущих измерений величин, входящих в уравнение измерения;
— сведения, имеющиеся в метрологических документах по поверки, калибровки и сведения изготовителя о приборе;
— сведения о предполагаемом вероятностном распределении значений величин, имеющихся в научно-технических отчетах и литературных источниках;
— данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих (подобных) СИ и материалов;
— неопределенность используемых констант и справочных данных;
— нормы точности измерений, указанные в технической документации на методы и СИ;
— другие сведения об источниках неопределенностей, влияющих на результат измерения.
Неопределенности этих данных обычно представляют в виде границ отклонения значения величины от ее оценки. Наиболее распространенный способ формализации неполного знания о значении величины заключается в постулировании равномерного закона распределения возможных значений этой величины в указанных границах ±bi для i-ой входной величины. При этом стандартную неопределенность по типу В определяют по следующей формуле
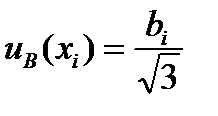
В случае других законов распределений формулы для вычисления неопределенности по типу В будут другие. В частности, если известно одно значение величины Xi, то это значение принимается в качестве оценки. При этом стандартную неопределенность вычисляют по формуле

где Up – расширенная неопределенность, k – коэффициент охвата. Если коэффициент охвата не указан, то, с учетом имеющихся сведений, принимают предположение о вероятностном распределении неопределенности величины Xi. Если такие сведения отсутствуют, то для определения коэффициента охвата можно воспользоваться данными таблицы П2.2 [П2.1].
Таблица П2.2
| Предполагаемое распределение неопределенности входной величины | Вероятность охвата Р, которой соответствует U ( x i ) | Коэффициент охвата k |
| 1,0 (предел допускаемых значений) | 3 | |
| 0,997 | 3 | |
| 0,99 | 2,6 | |
| 0,95 | 2 | |
| Неизвестное распределение | 2 |
При расширенной неопределенности, соответствующей вероятности P=0,99, коэффициент k= 0,9995· 

Если известны граница суммы неисключенных систематических погрешностей, распределенных по равномерному (равновероятному) закону θ(Р) или расширенная неопределенность в терминах концепции неопределенности Up, то коэффициент охвата при числе неисключенных систематических погрешностей m>4, зависит от доверительной вероятности. Коэффициент охвата kравен1,1 при Р=0,95; и1,4 при Р=0,99 [П2.1].
Неопределенности входных величин могут быть коррелированны. Для вычисления коэффициента корреляции r(xi, xq) используют согласованные пары результатов измерений 


Значимость коэффициента корреляции определяется критерием отсутствия или наличия связи между аргументами.
Вычисление суммарной неопределенности выходной величины проводят по тем же формулам, которые используются для расчета погрешностей косвенных измерений в классической концепции погрешности измерений.
В случае некоррелированных оценок входных величин, суммарную стандартную неопределенность 

и в случае коррелированных оценок – по формуле

Под бюджетом неопределенности понимается формализованное представление полного перечня источников неопределенности измерений по каждой входной величине с указанием их стандартной неопределенности и вклада их в суммарную стандартную неопределенность результата измерений.
Расширенная неопределенность равна произведению стандартной неопределенности u(y) результата измерений на коэффициент охвата k:
Руководство по неопределенности [П2.1] рекомендует рассматривать все результаты измерений при доверительной вероятности (вероятности охвата) Р=0,95. При этой вероятности преимущественно определяют число степеней свободы по эмпирической формуле Велча-Саттерствейта

При этом коэффициент охвата определяется при вероятности Р=0,95 с использованием таблицы распределения Стьюдента по формуле
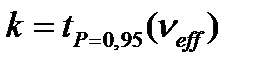
Коэффициент охвата ( 
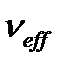 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 16 | 20 | 30 |  |
| tP=0,95 | 3,182 | 2,776 | 2,571 | 2,447 | 2,365 | 2,306 | 2,262 | 2,228 | 2,120 | 2,086 | 2,042 | 1,960 |
| tP=0,99 | 5,841 | 4,604 | 4,032 | 3,707 | 3,499 | 3,355 | 3,250 | 3,169 | 2,921 | 2,845 | 2,750 | 2,576 |
Формулу для оценки суммарной стандартной неопределенности (П2.7) можно записать в более простом виде


также как и формулу (П2.10) для определения числа степеней свободы

где 

При оценке вклада неопределенности (см.формулу П2.10) по типу А принимают 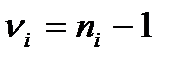
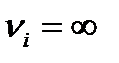

где nA – число повторных измерений входной величины, оцениваемой по типу А.
При представлении результатов измерений Руководство рекомендует приводить достаточное количество информации, чтобы можно было проанализировать и/или повторить весь процесс получения результата измерений и вычисления неопределенностей, а именно:
— алгоритм получения результата измерений;
— алгоритм расчета всех поправок для исключения систематических погрешностей и их неопределенней;
— неопределенности всех используемых данных и способы их получения;
Таким образом, в документации по результатам измерений необходимо представлять:
uc – суммарную неопределенность;
Up – расширенную неопределенность;
k – коэффициент охвата;
ui – данные о входных величинах;

Например, если результатом измерения является электросопротивление, то при оформлениирезультата измерений, записывают: «Электросопротивление резистора составляет 163,2 Ом. Расширенная неопределенность результата измерений составляет ± 2,4 Ом при коэффициенте охвата равном 2» или «измерения показали, что электросопротивление резистора находится в интервале (160,8 – 165,6) Ом при коэффициенте, равном 2». По умолчанию предполагается, что эти результаты соответствуют вероятности охвата 0,95.
Несмотря на то, что нормативный документ РМГ 43-2001[П2.2] на территории России не действует (вместо него введен в действие ГОСТ Р 54500-2011 [П2.3]), приведенные в нем примеры очень понятны и могут дать необходимое представление о том, как проводить оценку неопределенности результатов измерений.
Пример из РМГ 43-2001
1) Приведем данные, имеющиеся в распоряжении оператора, задача которого состоит в измерении силы тока с помощью вольтметра и токового шунта.
1 Составление уравнения измерения

где I – сила измеряемого тока, V – напряжение на шунте, которое непосредственно измеряется для определения силы тока, R– сопротивление шунта, t°C – температура окружающей среды, способная повлиять на результат измерения силы тока.
1.2. Производится многократное (n=10) измерение напряжения с помощью вольтметра на сопротивлении шунта при температуре t = (23,00±0,05)°С.
Границы неисключенной систематической погрешности вольтметра в милливольтах определены при его калибровке в виде следующего выражения:
1.3. Сопротивление шунта определено при его калибровке для тока величиной I=10 А и температуре t=23,00°C и равно R0 = 0,010 088 Ом. Относительные границы неисключеннойсистематической погрешности сопротивления шунта, установленные при его калибровке, равны
1.4. Границы неисключенной систематической составляющей погрешности значения сопротивления шунта, обусловленной погрешностью измерений температуры, находят из формулы, определяющей зависимость сопротивления от температуры
2 Нахождение результата измерений
В результате серии из n=10 измерений получают ряд значений Vi в милливольтах:
100,68; 100,83; 100,79; 100,64; 100,63; 100,94; 100,60; 100,68; 100,76; 100,65.
Среднеарифметическое вычисляют по формуле (П2.2)

Результат измерения силы тока получают по формуле

3 Анализ источников погрешности результата измерений
3.1. Среднеквадратическое отклонение (СКО), характеризующее случайную составляющую погрешности при измерениях напряжения 


Примечания. 1) Значок d здесь и далее обозначает относительное значение величины.
2) В соответствии с рекомендациями Руководства симметричные интервалы не обозначаются значками ±.
3.2. Границы неисключенной систематической погрешности вольтметра в милливольтах при 
3.3. Границы неисключенной систематической погрешности сопротивления шунта, в соответствии с (3-П2) и (4-П2), установленные при его калибровке, равны


3.4. Границы неисключенной систематической составляющей погрешности значения сопротивления шунта, обусловленной погрешностью измерений температуры в соответствии с (5-П2) равны
В дальнейшем эту составляющую погрешности ввиду ее малости по сравнению с другими составляющими можно не учитывать.
4 Вычисление характеристик погрешности результата измерений
Для вычисления результирующей погрешности измерения, состоящей из случайной погрешности и суммы неисключенных погрешностей, используется формула, принятая в Государственной системе обеспечения единства измерений для косвенных измерений:

Ниже приводится вычисление всех составляющих погрешностей, входящих в формулу (11-П2).
4.1. Делается предположение о равномерном распределении неисключенных систематических составляющих погрешности результата измерений внутри их границ qVи qR. Тогда СКО суммарной неисключенной систематической составляющей погрешности результата измерений силы тока Sq определяют по формуле

В этой формуле учтено, что коэффициенты влияния
4.2. Доверительные границы суммарной неисключенной систематической погрешности результата измерений силы тока q(р) при доверительной вероятности Р=0,95 оценивают по формуле
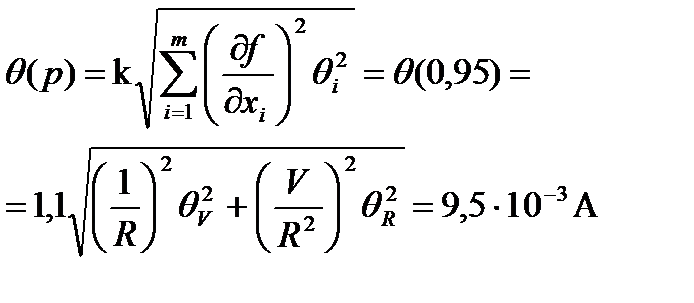
4.3. СКО случайной составляющей погрешности результата измерений силы тока S определяется по формуле

4.4. СКО суммарной погрешности результата измерений силы тока будет равно

4.5. Доверительные границы погрешности результата измерений силы тока при вероятности 0,95 и эффективном числе степеней свободы 
5 Вычисление неопределенности измерений
5.1. По типу А вычисляют стандартную неопределенность, обусловленную источниками неопределенности, имеющими случайный характер. Формула для вычислений подобна (7-П2)


Стандартную неопределенность силы тока, обусловленную источниками неопределенности, имеющими случайный характер, определяют по формуле

5.2. По типу В вычисляют стандартные неопределенности, обусловленные источниками неопределенности, имеющими систематический характер. Закон распределения величин внутри границ считают равномерным.
Границы систематического смещения при измерениях напряжения, определенные при калибровке вольтметра, определяются соотношением (2-П2). Тогда соответствующую стандартную неопределенность uB , V вычисляют по формуле

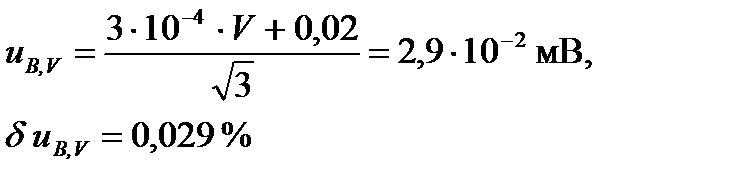

Границы изменения значения сопротивления шунта, обусловленного изменением температуры, равны 

В дальнейшем этой составляющей неопределенности ввиду ее малости по сравнению с другими составляющими можно пренебречь.
Суммарную стандартную неопределенность uB, вычисленную по типу В, определяют по формуле

5.3. Суммарную стандартную неопределенность uC вычисляют по формуле

5.4. Эффективное число степеней свободы 

5.5. Коэффициент охвата k находят по таблице 4 и определяют по формуле

5.6. Расширенную неопределенность U0,95 определяют следующим образом

6 Сравнение результата вычислений различными методами
Сравнение результата вычислений погрешности измерений в доверительном интервале, соответствующем вероятности Р=0,95 и расширенной неопределенности с коэффициентом охвата равном двум, т.е. соответствующем уровню доверия 0,95. совпадают и равны 0,012 А.
Следует отметить, что это не случайно, поскольку в основе расчетов лежат одни и те же измерительные данные и одни те же подходы к распределениям различных переменных. Сравнения результатов измерений, определенных с помощью классического подхода и концепции неопределенности, как показано на многочисленных примерах в различных публикациях дают одни и те же окончательные результаты [П2.1, П2.2].
Вообще расширенная неопределенность в концепции неопределенности не играет той роли, которая отводится в концепции погрешности. Считается, что основным результатом оценки является суммарная неопределенность uC, а расширенная неопределенность отличается от нее на постоянный коэффициент, который необходим в ряде специальных случаев для показа надежности оценки. Этот коэффициент может принимать значения от 2 до 3, при уровне доверия от 0,95 до 0,99.
Наши незнания об измеряемой величине определяются неопределенностью и группируются около результата измерения.
Список литературы, используемой в Приложении 2.
П2.1. А.Э. Фридман Основы метрологии. Современный курс. – С.-Пб.: НПО «Профессионал», 2008.
П2.2 РМГ 43-2001 Применение «Руководства по выражению неопределенности измерений», рекомендации по межгосударственной стандартизации, Межгосударственный совет по стандартизации, метрологии и сертификации, Минск, Изд-во стандартов, 2002
П2.3 ГОСТР 54500.1-2011/ Руководство ИСО/МЭК 98-1: 2009 Неопределенность измерения. Часть 1. Введение в руководства по неопределенностям измерения. – М.: Стандартинформ, 2012. – 17 с.