Погрешности измерений, представление результатов эксперимента

п.1. Шкала измерительного прибора

Примеры шкал различных приборов:

Манометр – прибор для измерения давления, круговая шкала

Вольтметр – прибор для измерения напряжения, дуговая шкала

Индикатор громкости звука, линейная шкала

п.2. Цена деления

Пример определения цены деления:

Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале: a = 5 c b = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.

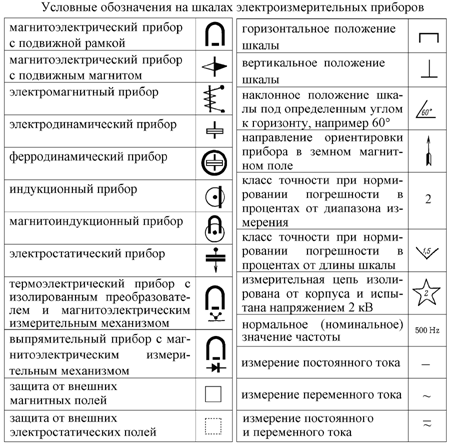
Цена деления: \begin \triangle=\frac\\ \triangle=\frac<10-5><24+1>=\frac15=0,2\ c \end

п.3. Виды измерений

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Определяется субъективным фактором, ошибками экспериментатора.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

Пример получения результатов прямых измерений с помощью линейки:

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

Сначала находим среднее значение всех измерений: \begin m_0=\frac<99,8+101,2+100,3><3>=\frac<301,3><3>\approx 100,4\ \text <г>\end Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности \(m_0\) и измерения. \begin \triangle_1=|100,4-99,8|=0,6\\ \triangle_2=|100,4-101,2|=0,8\\ \triangle_3=|100,4-100,3|=0,1 \end Находим среднее абсолютное отклонение: \begin \triangle_=\frac<0,6+0,8+0,1><3>=\frac<1,5><3>=0,5\ \text <(г)>\end Мы видим, что полученное значение \(\triangle_\) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: \begin \triangle m=max\left\<\triangle_; d\right\>=max\left\<0,5; 0,05\right\>\ \text <(г)>\end Записываем результат: \begin m=m_0\pm\triangle m\\ m=(100,4\pm 0,5)\ \text <(г)>\end Относительная погрешность (с двумя значащими цифрами): \begin \delta_m=\frac<0,5><100,4>\cdot 100\text<%>\approx 0,050\text <%>\end

п.6. Представление результатов эксперимента

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Мерой точности является относительная погрешность измерений. Получаем: \begin \delta_1=\frac<0,1><4,0>\cdot 100\text<%>=2,5\text<%>\\ \delta_2=\frac<0,03><4,0>\cdot 100\text<%>=0,75\text <%>\end Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: \(\delta_2\lt \delta_1\), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Источник

В какой части шкалы прибора измерение точнее и почему

Лабораторная работа №1

Ознакомление с электроизмерительными приборами и измерениями электрических величин.

Изучение электроизмерительных приборов, используемых в лабораторных работах, выполняемых на стенде. Получение представлений о пределе измерения и цене деления, абсолютной и относительной погрешности, условиях эксплуатации и других характеристиках стрелочных электроизмерительных приборов, получение навыков работы с цифровыми измерительными приборами.

2. Краткие теоретические сведения.

Контроль работы электрооборудования осуществляется с помощью разнообразных электроизмерительных приборов. Наиболее распространенными электроизмерительными приборами являются приборы непосредственного отсчета. По виду отсчетного устройства различают аналоговые (стрелочные) и цифровые измерительные приборы.

На лицевой стороне стрелочных приборов изображены условные обозначения, определяющие классификационную группу прибора. Они позволяют правильно выбрать приборы и дают некоторые указания по их эксплуатации.

В цепях постоянного тока для измерений токов и напряжений применяются в основном приборы магнитоэлектрической системы. Принцип действия таких приборов основан на взаимодействии магнитного поля постоянного магнита и измеряемого тока, протекающего по катушке. Угол поворота стрелки α прямо пропорционален измеряемому току I: α = К × I. Шкалы магнитоэлектрических приборов равномерные.

В измерительных механизмах электромагнитной системы, применяемых для измерений в цепях переменного и постоянного тока, вращающий момент обусловлен действием магнитного поля измеряемого тока в неподвижной катушке прибора на подвижный ферромагнитный якорь. Угол поворота стрелки α здесь пропорционален квадрату тока: α = К × 2I. Поэтому шкала электромагнитных приборов обычно неравномерная, что является недостатком этих приборов. Начальная часть шкалы не используется для измерений. Для измерений токов и напряжений в цепях переменного тока применяются также приборы выпрямительной системы. Такие приборы содержат выпрямительный преобразователь и магнитоэлектрический измерительный механизм. Они имеют более линейную шкалу, чем приборы электромагнитной системы и достаточно широкий частотный диапазон.

На лицевой стороне стрелочных прибора указывается класс точности, который определяет приведенную относительную погрешность прибора γ_ПР.

Приведенная относительная погрешность прибора – это выраженное в процентах отношение максимальной для данного прибора абсолютной погрешности ΔА к номинальному значению прибора (пределу измерений) A_НОМ:

Промышленность в соответствии с ГОСТ выпускает приборы с различными классами точности (0,05; 0,1; 0,2; 0,5; 1,5; 2,5; 4,0).

Зная класс точности прибора, можно определить абсолютную ΔА и относительную погрешности измерения γ_ИЗМ, а также действительное значение измеряемой величины A_Д:

Расчетную относительную погрешность измерения в любой точке шкалы прибора можно определить, полагая, что его допустимая абсолютная погрешность ΔА известна и постоянна:

где А_ИЗМ – условное измеренное значение величины, задаваемое в пределах

шкалы прибора от минимального значения до номинального значения данного прибора. Обратить внимание на значение относительной погрешности измерения, соответствующее предельному значению измеряемой величины, и сравнить его с классом точности прибора.

Нетрудно сделать вывод, что относительная погрешность измерения тем больше, чем меньше измеряемая величина по сравнению с номинальным значением прибора. Поэтому желательно не пользоваться при измерении начальной частью шкалы стрелочного прибора.

Для обеспечения малой методической погрешности измерения необходимо, чтобы сопротивление амперметра было значительно меньше сопротивления нагрузки, а сопротивление вольтметра было значительно больше сопротивления исследуемого участка.

В табл. 1 приведены некоторые условные обозначения, приводимые на лицевых панелях стрелочных измерительных приборов, определяющие их свойства и условия эксплуатации.

При проведении измерений в электрических цепях широкое применение получили цифровые измерительные приборы, например мультиметры – комбинированные цифровые измерительные приборы, позволяющие измерять постоянное и переменное напряжение, постоянный и переменный ток, сопротивления, проверять диоды и транзисторы. Представление результата измерения происходит на цифровом отсчетном устройстве в виде обычных удобных для считывания десятичных чисел. Наибольшее распространение в цифровых отсчетных устройствах мультиметров получили жидкокристаллические и светодиодные индикаторы. В лабораторном стенде используются цифровые приборы для измерения постоянных и переменных токов, а также цифровой измеритель мощности. Для переключения режима работы цифровых амперметров стенда (РА1, РА2, РА3 и РА4) на его передней панели установлен тумблер, который для измерения постоянного тока следует установить в позицию «=», для измерения действующих значений переменных токов – в позицию «

». Для измерения постоянного тока входная клемма (+) цифрового амперметра выделена красным цветом.

Цифровой измеритель мощности предназначен для измерения параметров электрической цепи:

– действующего значения напряжения U (True RMS) в диапазоне 0…30 В;

– действующего значения тока I (True RMS) в диапазоне 0…300 мА;

– активной мощности P в диапазоне 0…600 Вт;

– частоты f в диапазоне 35…400 Гц;

– угла сдвига фаз ϕ (Fi) между током и напряжением.

Условное графическое обозначение

Содержание условного обозначения

Наименование измеряемой величины (ампер, вольт, ватт, ом, герц, коэффициент мощности, фарада, генри)

Магнитоэлектрический измерительный механизм

Электромагнитный измерительный механизм

Магнитоэлектрический измерительный механизм с выпрямителем

0,05; 0,1; 0,2; 0,5; 1,5; 2,5; 4,0

Класс точности прибора

Рабочее положение шкалы прибора:

под углом, например 60°

Прибор предназначен для работы

в цепи постоянного тока;

постоянного и переменного;

в трехфазной цепи переменного тока

А (или отсутствие буквы) – прибор для сухих отапливаемых помещений с температурой +10°С …+35°С и влажности до 80% при 30°С;

B – приборы для полевых и морских условий:

Измерительная цепь прибора изолирована от корпуса и испытана напряжением, например, 2 кВ

Рабочий частотный диапазон прибора

– клеммы подачи входного измеряемого сигнала (генератора): клемму «Вх» и общую клемму, клеммы подключения потребителя (нагрузки): клемму «Вых» и общую клемму. Шунт для измерения тока нагрузки подключен между клеммами «Вх» и «Вых»;

– жидкокристаллический четырехстрочный индикатор для вывода информации;

– кнопку «f/cosϕ/ϕ» изменения вывода информации в четвертой строке индикатора (соответственно, частоты, коэффициента мощности cosϕ или угла сдвига фаз Fi между током и напряжением).

С задней стороны прибора установлены розетка для подключения питания сети и колодка предохранителя.

С помощью кнопки «f/cosϕ/ϕ» можно изменять вывод информации в четвертой строке индикатора. Для вывода требуемого параметра в четвертой строке индикатора кнопку необходимо нажать на 1…2 секунды.

3. Порядок выполнения работы.

3.1. Изучение паспортных характеристик стрелочных электроизмерительных приборов. Для этого внимательно рассмотреть лицевые панели стрелочных амперметров и заполнить табл. 2.

Характеристика электроизмерительного прибора

Источник

Шкала измерительного прибора, цена деления шкалы

Шкала — плоская или цилиндрическая поверхность, относительно которой движется стрелка, на которой нанесены деления.

Иногда шкала у прибора всего одна, а иногда их несколько, при этом индикатором измерений служит всего одна стрелка. Давайте же разберемся, что это за шкалы, и как ими пользоваться, чтобы ничего не напутать.

Для начала отметим, что шкалы эти бывают разными. Во-первых, более распространенными являются именованные шкалы, то есть шкалы, на которых деления проградуированы соответствующими единицами измеряемых величин, это градуированные шкалы.

Во-вторых, встречаются условные шкалы. Если прибор имеет несколько переключаемых пределов измерений, то шкала будет наверняка условной, и одни и те же деления будут иметь разные значения в каждом из установленных пользователем пределов.

Для того, чтобы по условной шкале прибора определить точно значение измеряемой в данный момент величины, необходимо, зная цену деления, количество делений до того места, куда отклонилась, и где остановилась в данный момент стрелка, умножить на цену деления.

Если цена деления не ясна, то ее можно легко найти, для этого берется разность между двумя известными значениями на шкале, и делится на количество делений между этими значениями. Например, известно, что красная шкала имеет ширину 10 вольт, а количество делений 50, значит цена деления для красной шкалы составляет 200 мВ.

Если на шкале есть отметка ноль, то шкала называется нулевой. Если нуля нет, то шкала называется безнулевой. Что касается нулевых шкал, то они, в свою очередь, подразделяются на односторонние и двухсторонние. На фото выше можно видеть сразу семь нулевых шкал.

У односторонних ноль размещен в самом начале шкалы (как на рисунке, головка вольтметра с односторонней шкалой), а у двухсторонних — по центру или между конечной и начальной отметками. Так, в зависимости от расположения нуля, двухсторонние шкалы подразделяются на несимметричные и симметричные.

Симметричная шкала ноль имеет по центру, несимметричная — не по центру шкалы. Если шкала безнулевая, то крайние отметки обозначают верхний и нижний пределы измерений. На фото выше изображен миллиамперметр с симметричной двухсторонней шкалой, цена деления составляет 50 мкА, поскольку 0,5 мА / 10 = 0,05 мА или 50 мкА.

В зависимости от характера связи угловых и линейных расстояний между двумя соседними делениями шкалы с измеряемыми величинами, шкалы бывают неравномерными, равномерными, логарифмическими, степенными и т. д. Для более точных измерений предпочтительней равномерные шкалы.

Когда отношение ширины самого широкого деления к самому узкому не более 1,3 при неизменной цене деления, шкалу уже можно считать равномерной.

На лицевой стороне измерительного прибора, недалеко от шкалы, как правило, размещены необходимые маркировки: единица величины измерения, ГОСТ, класс точности прибора, число фаз и род тока, категория защищенности данного измерительного прибора от внешних электрических и магнитных полей, условия эксплуатации, рабочее положение, предельное напряжение прочности изоляции измерительных цепей (на фото — в звездочке «2», значит 2 кВ), номинальная частота тока, если отличается от промышленных 50 Гц, например 500 Гц, положение относительно Земли, тип, система прибора, год выпуска, заводской номер, и прочие важные параметры.

В этой таблице приведены расшифровки основных обозначений, которые можно встретить на шкалах. Надеемся, что эта краткая статья поможет вам научиться правильно проводить измерения при помощи стрелочных измерительных приборов.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Лабораторная работа № 1. «Электроизмерительные приборы и измерения».

Ищем педагогов в команду «Инфоурок»

Лабораторная работа № 1.

«Электроизмерительные приборы и измерения».

Цель работы: Изучение электроизмерительных приборов, используемых в лабораторных работах.

Получение представлений о характеристиках стрелочных измерительных приборов. Получение навыков работы с цифровыми измерительными приборами.

Оборудование: Лабораторный стенд, четыре резистора, соединительные провода.

1) Изучение паспортных характеристик стрелочных электроизмерительных приборов.

Для этого внимательно рассмотрите лицевые панели стрелочных амперметров и заполните таблицу 1:

Система измерительного механизма

Максимальная абсолютная погрешность

Нормальное положение шкалы

2) Построить график зависимости относительной погрешности измерения от измеряемой величины для миллиамперметра переменного тока:

δ ,%

8

6

4

2

3) Ознакомиться с лицевой панелью мультиметра. Подготовьте мультиметр для измерения постоянного напряжения. Включить источник постоянного напряжения. Измерить значения выходных напряжений на клеммах «+5В», «+12В» и «-12В» относительно общей клеммы. Результаты измерений занесите в таблицу 2:

4) Подготовьте мультиметр для измерения переменного напряжения. Включить источник переменного напряжения. Измерить значения выходных напряжений на клеммах «А», «В», «С», «А-В», «В-С», «С- А». Результаты измерений занесите в таблицу 2:

Источник