в каком виде может быть задано решающее правило

Методы выбора окончательного решения (типы решающих правил) в задачах нормативной теории принятия решений.

Выявление системы предпочтений в рамках многокритериальной модели дает возможность перейти к формированию решающего правила.

В действительности лишь незначительная часть решений в той или иной прикладной области принимается на основе научных рекомендаций.

Основная часть действий, удовлетворяющих первичные (или биологические) потребности человека, производится автоматически, биологическими механизмами инстинктов и рефлексов. На втором месте по частоте применения стоит метод «проб и ошибок».

Достаточно естественным способом принятия решения является обращение к прошлому опыту, к стандартным, апробированным, стереотипным решениям.

Рассматривая вопрос формирования решающего правила, необходимо отметить, что решающее правило может быть задано в виде:

• аналитического выражения (например, метод обобщенного критерия);

• алгоритма (например, имитационная модель);

• словесной формулировки (метод Б. Франклина). Решающее правило, или метод принятия решения представляет собой способ сравнения наборов оценок по частным критериям (или векторных оценок) и вынесения суждений о предпочтительности одних наборов по отношению к другим. Методы, основанные на построении решающих правил, приводят множество альтернатив (допустимых решений) к такому упорядочению, которое соответствует содержательной постановке задачи и согласуется с ограничениями задачи и системой предпочтений ЛПР.

Методы принятия решений, или решающие правила классифицируются по различным признакам, например :

Вторая группа ориентирована на использование ограничений на критерии. Здесь можно выделить два направления:

• методы, являющиеся комбинацией методов главного и обобщенного критериев, где на некоторые критерии накладываются ограничения в соответствии с требованиями ЛПР, а из других критериев конструируется обобщенный критерий, который и максимизируют с учетом принятых ограничений;

Третью группу составляют методы, основанные на отыскании компромиссного решения. Чаще всего в данном случае речь идет о методах, ориентированных на гарантированный результат (максимин, минимакс). Смысл метода максимина в том, что наилучшим считается такое решение, при котором максимизируется всего один из критериев, а именно минимальный по значимости или по важности.

Источник

Большая Энциклопедия Нефти и Газа

Решающее правило

Решающее правило строится в зависимости от значений элементов объединенного вектора Ь1 ( ограничений на плановые задания, на сырье и на мощности. [1]

Решающее правило на каждом таксоне постоянно: векторы таксона относим в тот из распознаваемых классов, чьих представителей из обучающей выборки больше оказалось в данном таксоне. [5]

Решающее правило выдается в цифровой форме в виде значений порогов в каждом спектральном диапазоне. Коды величин порогов поступают на цифроаналоговые преобразователи, выходное напряжение которых используется в блоке обработки. Выходной сигнал блока обработки суммируется с анализируемым видеосигналом, в результате чего на экране монитора формируются контрастно окрашенные участки, соответствующие выбранным классам. [8]

Решающее правило задается критическим значением выборочной оценки ( вообще статистики), которому на диаграмме контрольной карты соответствует граница регулирования. [9]

Решающее правило и машинный порог дают возможность: а / осуществлять программу минимизации факторов, т.е. отбора из всей их совокупности тех сочетаний, которые являются наиболее информативными, б / выделять в отобранной минимизированной совокупности так называемые неуправляемые и управляемые факторы и подбирать в рамках фиксированного статистического распределения такие сочетания управляемых факторов, которые дают в прогнозе с некоторой вероятностью уменьшение относительного риска заболевания. [11]

Решающее правило определим следующим образом. [13]

Решающее правило этого типа называется последовательным критерием отношений вероятностей. [14]

Источник

Использование решающих правил

Рассмотрим теперь использование методов искусственного интеллекта для построения расписаний обработки заданий или деталей.

Как уже отмечалось, в настоящее время не существует регулярных алгоритмов решения задач теории расписаний (кроме задачи Джонсона), которые бы гарантировали получение оптимального решения.

Задачи теории расписаний, как уже отмечалось выше, относятся к NP-полным задачам, которые характеризуются следующим свойством: для этих задач неизвестны полиномиальные алгоритмы точного решения.

Наиболее эффективным подходом к решению задач теории расписаний, как показала практика их решения, оказался подход, использующий методы искусственного интеллекта.

Применение этих методов основано на использовании приоритетных или решающих правил, которые по существу являются некоторой модификацией продукционных правил.

Напомним, что продукционные правила в достаточно общем случае могут быть представлены в следующем виде:

Если то

иначе .

Условную часть правила часто посылкой правила, а и − заключением правила.

Простое продукционное правило может быть представлено в виде:

Если , то .

Решающее или приоритетное правило в достаточно общем случае может быть представлено в виде:

Если то ,

где − заключение правила, в котором почти всегда определяется порядок запуска детали на обработку, т. е. деталь, которая удовлетворяет условной части правила, обрабатывается первой или на участке или на станке.

Приоритетные правила условно можно разделить на два класса – простые и сложные.

К простым правилам относят правила с одним предусловием. Предусловия простых правил нельзя представить в виде совокупности некоторых предусловий.

Комбинированные приоритетные правила имеют предусловия, которые представляют собой комбинацию простых условий. Во многих случаях это позволяет точнее и в большей степени учитывать особенности производства и производственных программ, которые выполняются на этом производстве, что часто обеспечивает возможности быстрее получать весьма хорошие приближенные решения.

Приоритетные правила собирались, анализировались и формулировались на основе результатов многочисленных опросов наиболее успешных мастеров производственных участков и цехов, которые смогли организовать эффективную работу своих подразделений.

В настоящее время известно более нескольких тысяч приоритетных правил, хотя из них наиболее эффективными и, видимо, поэтому наиболее популярными и часто используемыми являются 350 – 450 правил. В данной главе нет возможности рассматривать большое количество различных простых приоритетных правил, поэтому рассмотрим лишь несколько из них.

1. Правило FCFS. Если деталь поступила первой, то первой и обслуживается.

2. Правило SPT – правило кратчайшей операции. Если время обработки детали на данной операции минимальное, то эта деталь обрабатывается в первую очередь.

Данное правило может быть использовано как для отдельного оборудования, так и для всей системы.

3. Правило LPT – максимально длинной операции. Если время обработки детали на данной операции максимально, то эта деталь обрабатывается в первую очередь.

Это правило также может быть использовано как для отдельного оборудования, так и для всей системы.

4. Правило LUKR – выбор работы, для которой длительность всех оставшихся операций минимальна, т. е.

Если длительность всех оставшихся операций обработки для детали минимальна, то данная деталь обрабатывается первой.

Данное правило может быть использовано, как для отдельного оборудования, так и для всей системы.

5. Правило MWKR – выбор детали, для которой длительность оставшихся операций максимальна.

Если у данной детали длительность всех оставшихся операций максимальна, то она обрабатывается первой.

Данное правило также может быть использовано как для отдельного оборудования, так и для производственного участка.

6. Правило FOPNR – минимального числа оставшихся невыполненных операций. Если количество невыполненных операций по обработке детали минимально, то эта деталь обрабатывается первой.

Данное правило также может быть использовано как для отдельного оборудования, так и для всего участка.

7. Правило DDATE – правило плановых сроков. Приоритет отдается деталям, плановые сроки готовности которых наступят раньше.

Если директивный срок готовности детали наиболее ранний, то деталь обрабатывается первой.

Правило может быть использовано как для отдельного оборудования, так и для всего участка.

8. Правило OPNDD – поэтапных плановых сроков. Приоритет определяется путем деления планового срока на длительность выполнения операции, т. е.

.

Возможны два варианта правила. Если величина минимальна, то -я деталь обрабатывается на -м оборудовании первой.

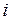
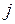
Если величина максимальна, то -я деталь обрабатывается на -м оборудовании первой.

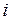
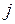
Такие правила называются антитетическими правилами. В одном из этих правил требуется первыми направить на обработку детали, у которых некоторые параметры принимают максимальное значение, а в другом наоборот, первыми должны обрабатываться детали, у которых эти параметры принимают минимальное значение.

Во многих случаях использование антитетических правил позволяет значительно быстрее получить подходящее приближение к решению поставленной задачи.

При использовании простых решающих правил часто могут возникать ситуации, когда с их помощью не удается получить однозначного порядка запуска деталей.

Ситуацию, когда после применения решающего правила несколько деталей претендуют на обработку первыми, называют конфликтной ситуацией.

Для разрешения конфликтных ситуаций полезными оказываются следующие два приема.

Когда после использования первого простого правила возникает конфликтная ситуация и образуется множество деталей, претендующих на обработку в первую очередь, то к этому множеству деталей применяется следующее решающее правило. Если в результате использования второго решающего правила конфликтная ситуация не будет исчерпана, то ко вновь образовавшемуся множеству деталей, претендующих на обработку в первую очередь применяется следующее решающее правило и т. д. Это продолжается до тех пор, пока конфликтная ситуация не будет исчерпана.

При использовании следующего приема в случае возникновения конфликтной ситуации ко множеству деталей, претендующих на обработку в первую очередь, применяется комбинированное правило, в котором имеется предусловие, задающее однозначный порядок запуска деталей. Например, такое правило может иметь следующий вид:

Если номер детали минимальный, то ,где предусловие «номер детали минимальный» позволяет установить однозначный порядок запуска деталей на обработку.

В качестве примеров комбинаторных решающих правил рассмотрим следующие правила.

1. Если время обработки детали на данной операции меньшее и время оставшихся операций по обработке детали меньше, то эта деталь обрабатывается в первую очередь.

2. Если длительность всех оставшихся операций по обработке данной детали максимальна и при этом ее номер меньше, то эта деталь обрабатывается первой.

3. Если количество невыполненных операций по обработке детали максимально и для таких деталей время оставшихся операций минимально и номер детали меньше, то эта деталь обрабатывается первой.

Использование приоритетных правил для решения задач теории расписаний можно весьма удобно пояснить с помощью следующей схемы, представленной на рис. 10.28.

После ввода исходных данных из списка правил, включающих 15 – 25 правил, выбирается первое правило, с использованием которого определяется порядок запуска деталей на обработку на каждом станке.

Затем производится имитация обработки введенной производственной программы на оборудовании производственного участка. Для этого моделируется поступление каждой детали на станки, используемые для их обработки, в соответствии с технологическим маршрутом обработки детали и выбранным ранее порядком ее обработки.

Рис.10.28. Схема использования решающих правил для построения расписания обработки деталей.

Если станок, на который должна поступить деталь, занят, то деталь ожидает его освобождения. Если станок свободен, а деталь еще не закончила обработку на предыдущем по технологии станке, и нет других деталей для обработки на этом станке, то станок простаивает в ожидании детали.

В результате имитации обработки введенной производственной программы на оборудовании производственного участка определяется значение критерия , который используется для оценки и выбора наиболее подходящего расписания. Полученное значение критерия полагается равным рекорду .

После этого из списка правил выбирается второе правило, с использованием которого определяется другой порядок запуска деталей на обработку на каждом станке.

Затем в соответствии с этим порядком запуска деталей производится новая имитация обработки введенной производственной программы на оборудовании производственного участка и определяется другое значение критерия , которое сравнивается со временем рекорда .

Если окажется, что у вновь полученного расписания значение критерия при минимизации критерия оказалось больше или равно значению рекорда ( ), то вновь полученное расписание забывается, а значение рекорда сохраняется.

Если же у вновь полученного расписания значение критерия при минимизации критерия окажется меньше значения рекорда ( ), то значение критерия для вновь полученного расписания становится значением рекорда, т. е. , а старое рекордное расписание забывается.

После этого весь описанный выше процесс повторяется для третьего, четвертого и так вплоть до последнего правила. В результате таких операций будет построено и выбрано расписание с лучшим значением используемого критерия.

Здесь хотелось бы отметить некоторые особенности решающих правил и их использования при построении расписаний.

На начальном этапе развития методов, использующих для построения расписаний решающих правил, появились иллюзии, что из всего известного множества решающих правил можно выбрать некоторое ограниченное количество правил, которые позволят эффективно решать самые разные задачи теории расписаний.

Однако дальнейшие исследования показали, что это совсем не так. Хорошо работающие для одних производственных систем и их производственных программ решающие правила оказываются совсем неэффективными для других систем и наоборот. Выделить универсальные решающие правила для построения расписаний работ в различных производственных системах не удалось. По-видимому, таких универсальных правил вообще не существует.

Как показал опыт и вычислительные эксперименты, из достаточно большого множества решающих правил при построении расписаний обработки типовых производственных программ для конкретных производственных систем лучшими оказываются 15 – 25 решающих правил.

Поэтому для повышения эффективности систем планирования, в которых при построении расписаний работ используются решающие правила, их приходится «настраивать» на конкретные производственные системы или участки и их производственные программы.

Для этого, как показано на рис. 10.28, используется база правил, содержащая 250 – 350 решающих правил, и с ее помощью строятся расписания работ по выполнению типовых производственных программ на конкретном производственном участке. Решающим правилам, с использованием которых получают лучшие результаты, присваивают рейтинговые баллы. Величина рейтинговых баллов зависит от результата, который был получен с помощью конкретного правила. После решения каждой задачи, полученные рейтинговые баллы правила прибавляются к ранее приобретенным баллам.

В результате решения типовых задач будут выделены наиболее эффективные для производственного участка решающие правила, которые и включаются в Список из 15 – 25 решающих правил.

Дело в том, что использование всех решающих правил, имеющихся в базе правил, при построении расписаний обработки будет занимать весьма значительное время, хотя эффективно из них будет работать лишь небольшая часть правил, которую обычно и стараются включить в Список правил.

Однако иногда возникают ситуации, когда с помощью решающих правил из Списка не удается получить расписание, которое смогло бы удовлетворить пожелания заказчика.

Для того чтобы увеличить возможности системы и улучшить качество ее работы в таких ситуациях в Список решающих правил на последней позиции включается процедура, обеспечивающая случайный порядок запуска деталей на обработку, что еще и обеспечивает однозначный выбор порядка запуска деталей на обработку. Эта процедура, как уже отмечалось выше, обычно используется в тех случаях, когда применение решающих правил не дало хорошего результата. Прекращение имитационных экспериментов с использованием этой процедуры обычно происходит как по критерию построения расписания, так и по времени моделирования.

Операции по определению порядка запуска деталей на обработку и имитация обработки деталей на схеме, представленной на рис.10.28, объединены в один блок с пунктирными границами. Это связано с тем, что при решении одних задач с использованием приоритетных правил можно определять порядок запуска деталей на обработку для всей производственной системы. Однако при решении других задач, когда приходится определять порядок запуска деталей на каждый конкретный станок, назначение детали на обработку может производиться только после завершения обработки на этом станке предшествующей детали. Поэтому операции по определению порядка запуска детали на обработку и имитации обработки детали приходится выполнять последовательно для каждой детали на всех станках.

Источник

Решающие правила в теории распознавания состояний

Здравствуйте, уважаемые форумчане!

Сложно себе представить жизнь человечества без распознавания протекающих природных и техногенных процессов, без диагностики и точного прогноза событий, без раннего выявления или обнаружения разного рода аномальных явлений и процессов, порой угрожающих жизни людей. Вряд ли кто-то оспорит тезис, что быстрое установление истинного диагноза в разных сферах человеческой деятельности и повышение точности прогнозирования способствует раннему управляющему воздействию для предотвращения тяжких последствий, способствует повышению общественной безопасности.

Известный российский ученый Дмитрий Завельевич Уздин длительное время занимался изучением проблематики решения задач скорейшего обнаружения и прогноза аномальных, деструктивных, нездоровых, неисправных и других опасных состояний в жизни людей и окружающего природного и техногенного мира. Результатом этих трудов стала книга «Новые меры близости, функции состояний и решающие правила в теории распознавания состояний (статистической классификации)», которую и предлагаю Вашему вниманию.

К опасным состояниям, о которых идет речь, относятся:
• опасные заболевания;
• отказы сложных технических систем;
• землетрясения;
• экономические и финансовые кризисы, а также многие другие нежелательные явления и процессы.

Теперь несколько слов от самого Дмитрия Завельевича: «Приветствую дорогие форумчане! Новые, более эффективные меры близости разработаны мной с целью более раннего установления истинного диагноза (ИД) не только в сфере медицины, но и в других областях знаний. Эта методика может быть эффективно использована при решении сложных задач диагностики и прогноза различных состояний, характеризуемых недостаточным числом информативных, специфичных параметров-признаков, в результате чего области известных, эталонных диагнозов (среди которых ИД) существенно пересекаются, и их разделение с установлением ИД, становится проблематичным
Правила принятия решений при установлении ИД основаны на 3-х, сформулированных мною, принципах распознавания состояний, позволяющих в этих сложных условиях диагностики, разделить эти диагнозы и, используя новые меры близости, установить ИД на ранней стадии заболевания, либо выявить износ деталей, либо раньше обнаружить трещины в металлических конструкциях, либо начавшееся развитие экономического кризиса и других опасных или нежелательных процессов».

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Источник