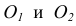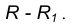в каком месте должна находиться точка сопряжения дуги с дугой

В каком месте должна находиться точка сопряжения дуги с дугой

§ 9. Сопряжения

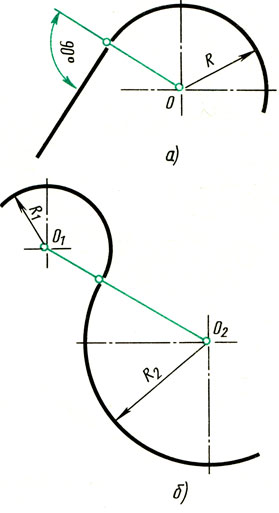
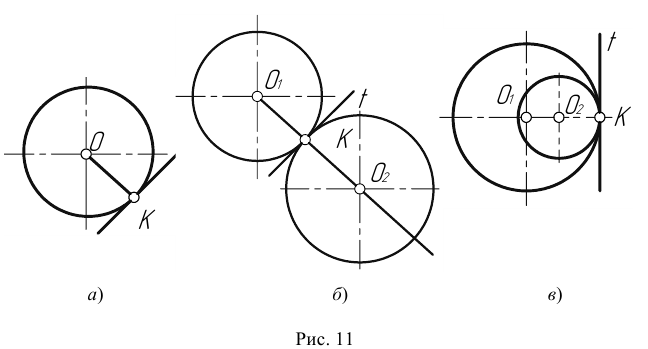
Плавный переход прямой линии в дугу или одной дуги в другую называют сопряжением. Для построения сопряжения надо найти центры, из которых проводят дуги, т. е. центры сопряжений (рис. 63). Затем нужно найти точки, в которых одна линия переходит в другую, т. е. точки сопряжений. При построении контура изображения сопрягающиеся линии нужно доводить точно до этих точек. Точка сопряжения лежит на перпендикуляре, опущенном из центра О дуги на сопрягаемую прямую (рис. 64, а), или на линии О₁О₂, соединяющей центры сопрягаемых дуг (рис. 64, б). Следовательно, для построения любого сопряжения дугой заданного радиуса нужно найти центр сопряжения и точку сопряжения.

Рис. 63. Элементы сопряжений

Рис. 64. Определение точки сопряжения

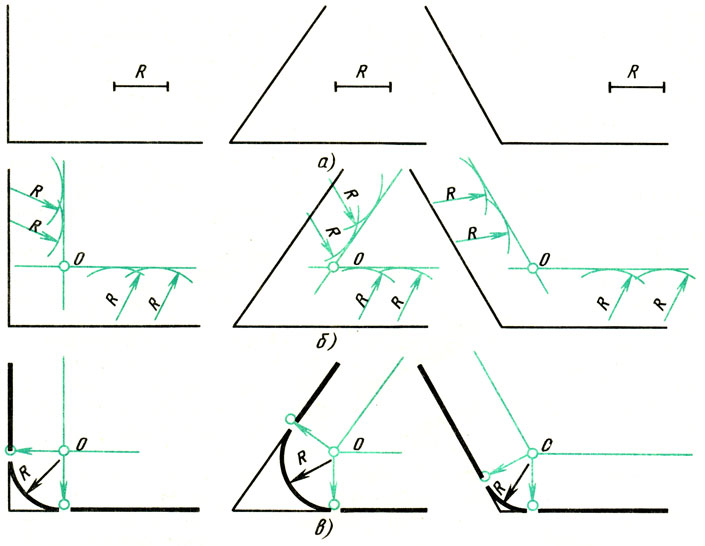
Сопряжение двух пересекающихся прямых дугой заданного радиуса. Даны пересекающиеся под прямым, острым и тупым углами прямые линии (рис. 65, а). Нужно построить сопряжения этих прямых дугой заданного радиуса R.

Для всех трех случаев применяют общий способ построения.

Для построения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R, делают засечки и к ним проводят касательные.

2. Находят точки сопряжений (рис. 65, в). Для этого опускают перпендикуляры из точки О на заданные прямые.

3. Из точки О, как из центра, описывают дугу заданного радиуса R между точками сопряжений (рис. 65, в).

Рис. 65. Сопряжение двух пересекающихся прямых

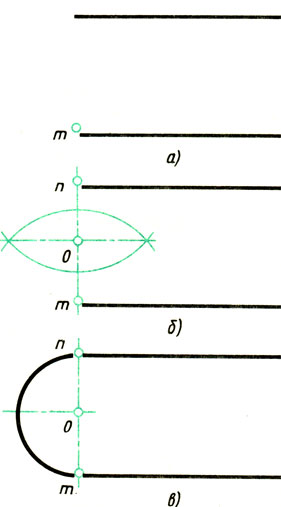
Сопряжение двух параллельных прямых. Заданы две параллельные прямые и на одной из них точка сопряжения т (рис. 66, а). Требуется построить сопряжение.

Построение выполняют следующим образом:

1. Находят центр сопряжения и радиус дуги (рис. 66, б). Для этого из точки m на одной прямой восставляют перпендикуляр до пересечения с другой прямой в точке п. Отрезок делят пополам (см. рис. 56).

Рис. 66. Сопряжение двух параллельных прямых

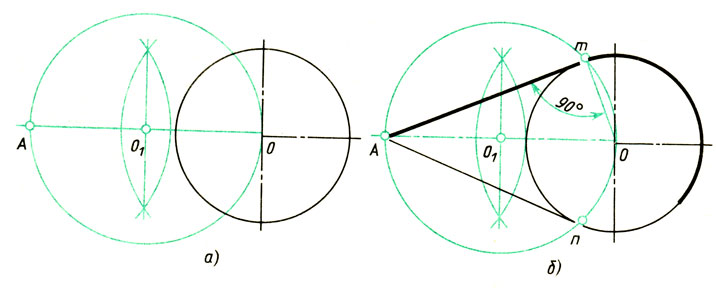
Проведение касательной к окружности. Задана окружность с центром О и точка А (рис. 67, а). Требуется провести из точки А касательную к окружности.

1. Точку А соединяют прямой с заданным центром О окружности.

Строят вспомогательную окружность диаметром, равным ОА (рис. 67, а). Чтобы найти центр О₁ делят отрезок ОА пополам (см. рис. 56).

Рис. 67. Построение касательной к двум окружностям

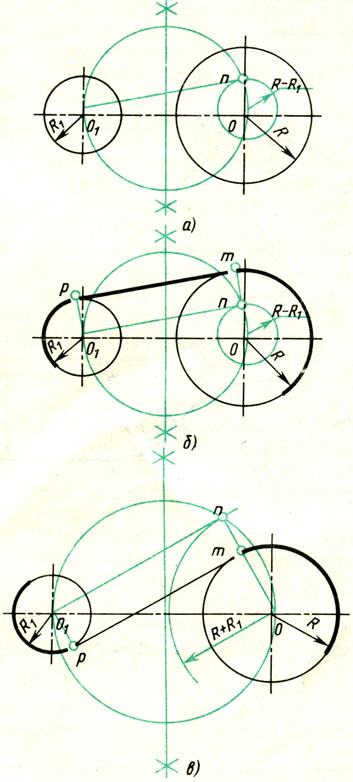
Проведение прямой, касательной к двум окружностям. Заданы две окружности радиусом R и R₁. Требуется построить касательную к ним.

Различают два случая касания: внешнее (рис. 68, б) и внутреннее (рис. 68, в).

При внешнем касании построение выполняют следующим образом:

2. Радиус, проведенный из точки О в точку n, продолжают до пересечения в точке m с заданной окружностью радиусом R. Параллельно радиусу Оm проводят радиус 0₁р меньшей окружности. Прямая, соединяющая точки сопряжений m и р,- касательная к заданным окружностям (рис. 68, б).

При внутреннем касании построение проводят аналогично, но вспомогательную окружность проводят радиусом, равным сумме радиусов R + R₁ (см. рис. 68, в). Затем из центра O₁ проводят касательную к вспомогательной окружности (см. рис. 67). Точку n соединяют радиусом с центром О. Параллельно радиусу On проводят радиус O₁р меньшей окружности. Искомая касательная проходит через точки сопряжений m и р.

Рис. 68. Построение касательной к окружности

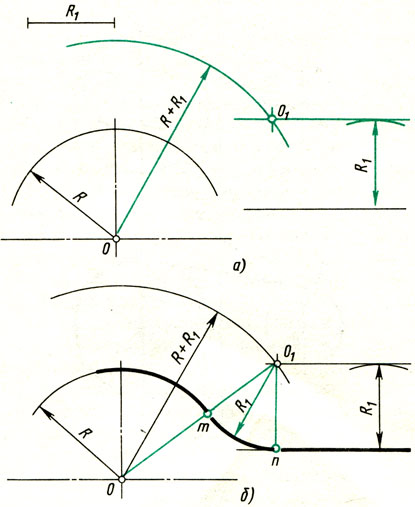
Сопряжение дуги и прямой линии дугой заданного радиуса. Заданы дуга окружности радиусом R и прямая. Требуется соединить их дугой радиусом R₁.

1. Находят центр сопряжения (рис. 69, а), который должен находиться на расстоянии R₁ от дуги и от прямой. Такому условию соответствует точка пересечения прямой линии, параллельной заданной прямой, проходящей от нее на расстоянии R₁, и вспомогательной дуги, отстоящей от заданной также на расстоянии R₁. Поэтому проводят вспомогательную прямую, параллельную заданной прямой, на расстоянии, равном радиусу сопрягающей дуги R₁ (рис. 69, а). Раствором циркуля, равным сумме заданных радиусов R + R₁, описывают из центра О дугу до пересечения с вспомогательной прямой. Полученная точка O₁— центр сопряжения.

2. По общему правилу находят точки сопряжения (рис. 69, б). Соединяют прямой центры сопрягаемых дуг O₁ и О. Опускают из центра сопряжения O₁ перпендикуляр на заданную прямую.

3. Из центра сопряжения O₁ между точками сопряжения m и n проводят дугу, радиус которой равен R 1 (см. рис. 69, б).

Рис. 69. Сопряжение дуги окружности и прямой

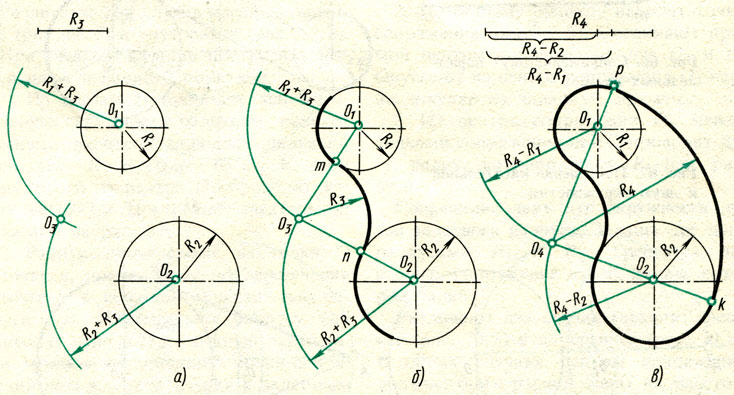
Сопряжение двух дуг окружности дугой заданного радиуса. Заданы две дуги радиусами R₁ и R₂. Требуется построить сопряжение дугой, радиус которой задан.

Различают два случая касания: внешнее (рис. 70, б) и внутреннее (рис. 70, в). В обоих случаях центры сопряжений должны быгь расположены на расстоянии, равном радиусу дуги сопряжения, от заданных дуг. По общему правилу на прямых, соединяющих центры сопрягаемых дуг, находят точки сопряжения.

Ниже приведен порядок построения для внешнего и внутреннего касаний.

2. Соединив прямыми точку O₁ с точкой O₃ и точку O₂ с точкой O₃, находят точки сопряжения m и n (см. рис. 70, б),

3. Из точки О₃ раствором циркуля, равным R₃, между точками m и n описывают сопрягающую дугу.

Для внутреннего касания выполняют те же построения, но радиусы дуг берут равными разности радиусов сопрягающей и заданной дуг, т.е. R₄-R₁ и R₄-R₂. Точки сопряжения р и k лежат на продолжении линий, соединяющих точку О₄ с точками O₁ и O₂.

Рис. 70. Сопряжение двух дуг окружности

Источник

Правила оформления чертежей Задание Вопрос Какими размерами опре. Правила оформления чертежей Задание Вопрос Какими размерами определяются форматы чертежных листов

Правила оформления чертежей

Вопрос 1. Какими размерами определяются форматы чертежных листов?

4) Размерами внешней рамки, выполняемой сплошной тонкой линией;
Вопрос 2. Где располагается основная надпись чертежа по форме 1 на чертежном листе?

5) В правом нижнем углу, примыкая к рамке формата.
Вопрос 3. Толщина сплошной основной линии в зависимости от сплошности изображения и формата чертежа лежит в следующих пределах?

2) 1:1; 1:2; 1:2,5; 1:4; 1:5; 2:1; 2,5:1; 4:1; 5:1.

Вопрос 1. Размер шрифта h определяется следующими элементами?

2) Высотой прописных букв в миллиметрах;
Вопрос 2. ГОСТ устанавливает следующие размеры шрифтов в миллиметрах?

4) 1,8; 2,5; 3,5; 5; 7; 10; 14; 20.
Вопрос 3. Толщина линии шрифта d зависит от?

2) От высоты строчных букв шрифта;
Вопрос 4. В соответствии с ГОСТ 2.304-81 шрифты типа А и Б выполняются?

2) Без наклона и с наклоном около 75 0 ;
Вопрос 5. Какой может быть ширина букв и цифр стандартных шрифтов?

4) Ширина букв и цифр определяются высотой строчных букв;
Задание 3.

Вопрос 1. В каких единицах измерения указываются линейные и угловые размеры на чертежах?

1) В сотых долях метра и градусах;
В опрос 2. При нанесении размера дуги окружности (части окружности) используют следующий знак?

1) R;
Вопрос 3. На (Рис. СЗ-1) показаны шрифты правильных и ошибочных расположений размерных линий. Определите, под каким номером обозначен правильный чертеж?

5) Правильный вариант ответа №5;
В опрос 4. Определите, на каком чертеже правильно записаны размерные числа (см. Рис. СЗ-2)?

4) Правильный вариант ответа №4;
Вопрос 5.

Н а каком чертеже правильно нанесены величины диаметра и квадрата (см. Рис. СЗ-3)?

3) Правильный вариант ответа №3;

Вопрос 1. Какими линиями выполняют вспомогательные построения при выполнении элементов геометрических построений?

2) Сплошными тонкими;
Вопрос 2. На каком расстоянии от контура рекомендуется проводить размерные линии?

1) Не более 10 мм;
Вопрос 3. На каком расстоянии друг от друга должны быть параллельные размерные линии?

1) Не более 7 мм;
Вопрос 4. Чему должен быть равен раствор циркуля при делении окружности на шесть равных частей?

5) Радиусу окружности.
В опрос 5. В каком случае показано правильное расположение центровых линий окружностей (см. Рис. СЗ-4)?

5) Правильный вариант ответа №5;

Вопрос 1. В каком месте должна находиться точка сопряжения дуги с дугой?

2) На линии, соединяющей центры сопряжений дуг;
Вопрос 2. Уклон 1:5 означает, что длина одного катета прямоугольного треугольника равна?

5) Одной единице, а другого пяти.
Вопрос 3. Какие проставляются размеры при выполнении чертежа в масштабе, отличном от 1:1?

5) Размеры должны быть увеличены или уменьшены в соответствии с масштабом.
Вопрос 4. Конусность 1:4 означает, что?

Вопрос 1. Точка может быть однозначно определена в пространстве, если она спроецирована?

4) На три плоскости проекций;
Вопрос 2. Как расположена в пространстве горизонтальная плоскость проекций? Координатного треугольника?

4) Параллельно плоскости V;
Вопрос 3. Профильная плоскость проекций для координатного трехгранника вводится?

5) Перпендикулярно плоскостям Н и V.
Вопрос 4. Трехгранный комплексный чертеж образуется?

3) Поворотом плоскости Н вниз, а плоскости W вправо на 90 0 ;
Вопрос 5. Линия связи на трехкартинном комплексном чертеже, соединяющая горизонтальную и фронтальную проекции точек, проходит?

4) Под углом 90 0 к оси x;

Вопрос 1. Отрезок общего положения в пространстве расположен?

2) Перпендикулярно плоскости V;
Вопрос 3. Горизонтальная прямая или сокращенно горизонталь расположена?

1) Параллельно плоскости Н;
Вопрос 4. Сколько Вы знаете вариантов задания проекций плоскостей на комплексном чертеже?
2) Три и четыре дополнительных;
Вопрос 5. Может ли фронтально-проецирующая плоскость одновременно быть профильной плоскостью?

4) Может, если она параллельна профильной плоскости проекций W;

Вопрос 1. Для построения проекции точки в прямоугольной приведенной изометрии пользуются следующим правилом?

1) Откладывают по всем осям отрезки, равные натуральным величинам координат;
Вопрос 2. В прямоугольной приведенной изометрии проекции окружности в плоскостях, параллельных трем плоскостям координатного трехгранника будут?

3) Все три одинаковые;

Вопрос 3. Как располагаются координатные оси в прямоугольной изометрии относительно друг друга?

4) Под углами 120 0 друг к другу;
Вопрос 4. Как располагаются оси в прямоугольной диметрии по отношению к горизонтальной прямой?

Вопрос 1. Для прямой призмы число боковых сторон будет равно?

4) Числу сторон многоугольника в основании;
Вопрос 2. Чему равно расстояние между центрами эллипсов (по высоте) для прямоугольной изометрии прямого кругового цилиндра?

1) Диаметру окружности основания цилиндра;
Вопрос 3. Боковые стороны пирамиды представляют собой?

5) Треугольники.
Вопрос 4. Для определения недостающей проекции точки, принадлежащей поверхности конуса, через известную проекцию точки можно провести?

1) Образующую или окружность, параллельную основанию;
Вопрос 5. Высота конуса (расстояние от центра эллипса до вершины) в прямоугольной изометрии равна?

3) Высоте конуса (расстоянию от центра окружности до вершины) на комплексном чертеже;

Основы технического черчения.

Вопрос 1. Какое максимальное количество видов может быть на чертеже детали?

Вопрос 2. Сколько видов должно содержать изображение какой-либо конкретной детали?

3) Минимальное, но достаточное для однозначного уяснения конфигурации;

Вопрос 3. Какой вид называется дополнительным?

4) Полученный проецированием на плоскость, не параллельную ни одной из плоскостей проекций;

Вопрос 4. Что называется местным видом?

1) Изображение только ограниченного места детали;

Вопрос 5. Какой вид детали и на какую плоскость проекций называется ее главным видом?

1) Вид сверху, на плоскость Н;

2) Вид спереди, на плоскость V;

3) Вид слева, на плоскость W;

4) Вид сзади, на плоскость Н;

5) Дополнительный вид, на дополнительную плоскость.
Задание 2.

Вопрос 1. Даны два вида деталей: главный вид и вид слева. Определите вид сверху из предложенных вариантов.

3) Правильный вариант ответа №3;

В опрос 2. Определить вид слева детали по заданным главному виду и виду сверху. (см. Рис. С3-7)

4) Правильный вариант ответа №4;

Вопрос 4. Когда на чертеже делают надписи названий основных видов?

4) Когда нужно показать дополнительный вид;
Вопрос 5. Возможно ли выполнение дополнительных видов повёрнутыми?

5) Возможно, но дополнительный вид выполняется только в проекционной связи по отношению к главному.

Вопрос 3. Какие разрезы называются горизонтальными?

Вопрос 5. Какие вы знаете вертикальные разрезы?

1) Горизонтальный т фронтальный;

3) Горизонтальный и наклонный;

4) Наклонный и фронтальный;

5) Фронтальный и профильный.

Вопрос 1. Простой разрез получается при числе секущих плоскостей, равных:

2) Перпендикулярно друг другу;

Вопрос 4. Всегда ли нужно обозначать простые разрезы линией сечения?

1) Да, обязательно;
Вопрос 5. В каком случае можно соединять половину вида с половиной соответствующего разреза?

4) Если вид и разрез являются симметричными фигурами;

Вопрос 1. Если вид и разрез являются симметричными фигурами, то какая линия служит осью симметрии, разделяющей их половины?

5) Штрих-пунктирная тонкая.

Вопрос 2. Как изображаются на разрезе элементы тонких стенок типа рёбер жесткости, зубчатых колёс?

4) Показываются рассечёнными, но штрихуются в другом направлении по отношению к основной штриховке разреза;
Вопрос 3. Какого типа линией с перпендикулярной ей стрелкой обозначаются разрезы (тип линий сечения).

1) Сплошной тонкой линией;
Вопрос 4. Как проводят секущие плоскости при образовании разрезов на аксонометрических изображениях,

например, при выполнении выреза четверти детали.

2) только параллельно координатным плоскостям;

Вопрос 5. Как направлены линии штриховки разрезов на аксонометрических проекциях?

4) Параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям.

З адание 6.

Вопрос 4. На каком изображении детали правильно выполнен её разрез (рис. С3-12)?

4) На четвертом изображении;
В опрос 5. Под каким углом осуществляется штриховка металлов (графическое изображение металлов) в разрезах?

5) Под углом 75 градусов к линии основной надписи чертежа;
Задание 7.

Вопрос 3. В каком случае правильно выполнено совмещение вида с разрезом (см. Рис. С3-13)?

Вопрос 5. Всегда ли обозначается положение секущих плоскостей при сложных разрезах?

Вопрос 1. В сечении показывается то, что:

Вопрос 2. Контур вынесенного сечения выполняется:

3) Волнистой линией;

Вопрос 3. На рисунке С3-15 показана деталь и дано её сечение. Из нескольких вариантов сечения выберите правильный.

Вопрос 5. Как обозначают несколько одинаковых сечений, относящихся к одному предмету?

2) Никак не обозначают;

Вопрос 1. Дана деталь и указано ее сечение А-А (рис.С3-17-а). Выбрать правильный вариант сечения.

3) Правильный вариант ответа №3;
Вопрос 2. Дана деталь и указано ее сечение А-А (рис.С3-17-б). Выбрать правильный вариант сечения.

4) Правильный вариант ответа №4;

Вопрос 3. Дана деталь и указано ее сечение А-А (рис.С3-17-в). Выбрать правильный вариант сечения.

1 ) Правильный вариант ответа №1;

Источник

Сопряжения в инженерной графике на чертежах с примерами

Содержание:

В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.

Точка касания К и центры окружностей

Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.

Сопряжение двух пересекающихся прямых линий

Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.

Выполним следующие построения:

Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.

Сопряжения прямой с окружностью

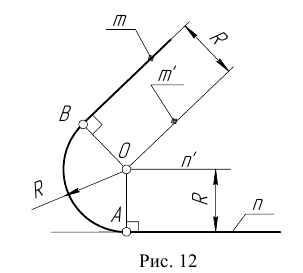
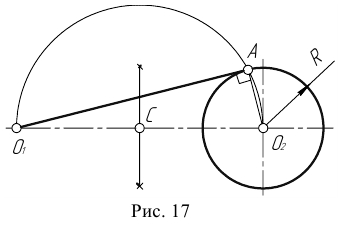
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.

Пример 1. Пусть задана окружность радиусом R с центром в точке и прямая m. Требуется построить сопряжение окружности с прямой дугой окружности заданного радиуса R (рис. 13).

Для решения задачи выполним следующие построения:

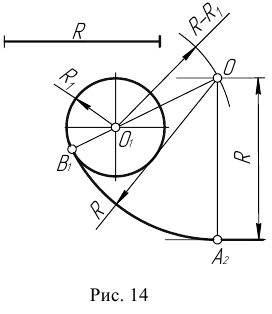
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра , радиусом

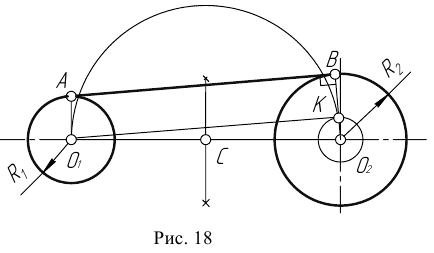
Сопряжение двух окружностей

Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.

Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 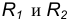дугой заданного радиуса R (рис. 15а).

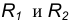
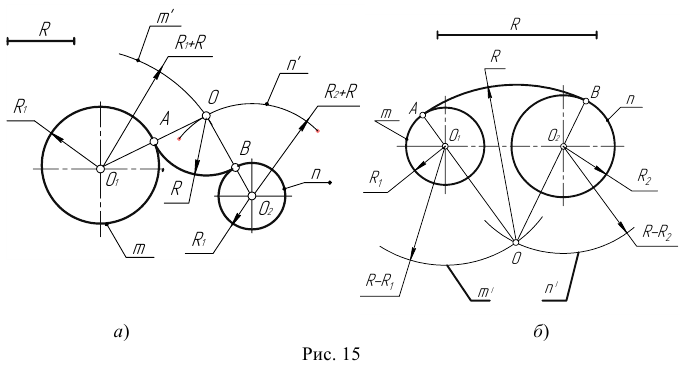
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами дугой радиусом R (рис. 15б).

Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.

Построение касательных

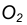
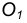
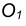
Пример 1. Дана окружность с центром в точке и точка вне её. Через данную точку провести касательную к данной окружности (рис. 17).

Для решения задачи выполним следующие построения.

Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 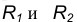(рис. 18).

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник