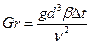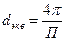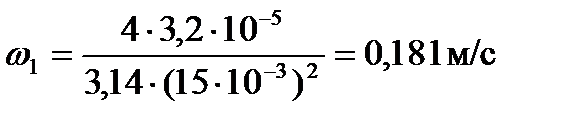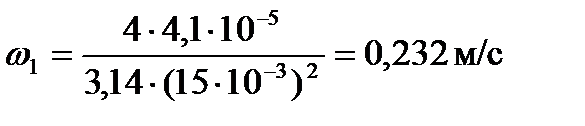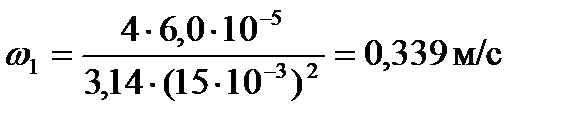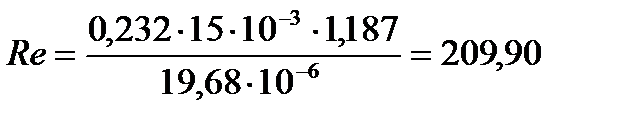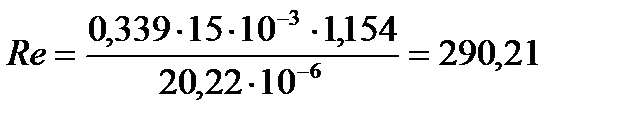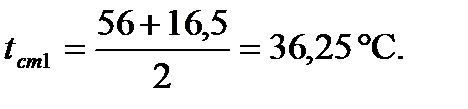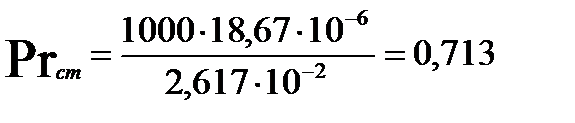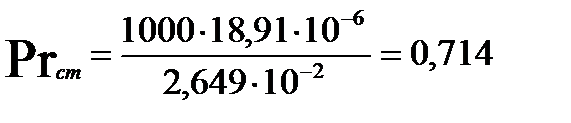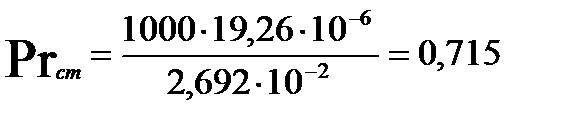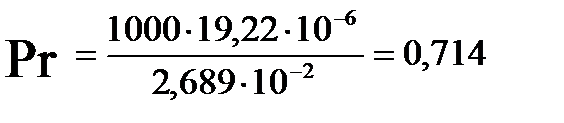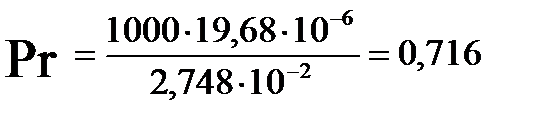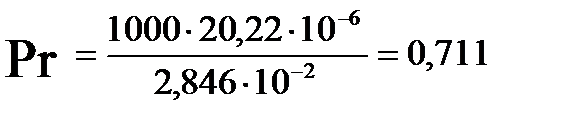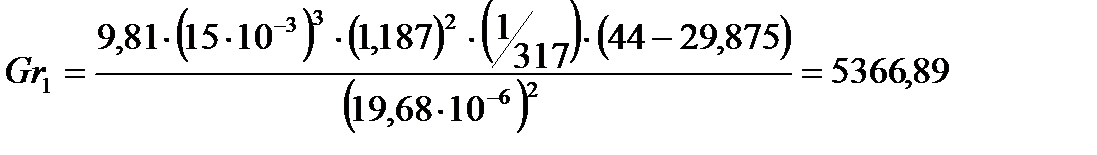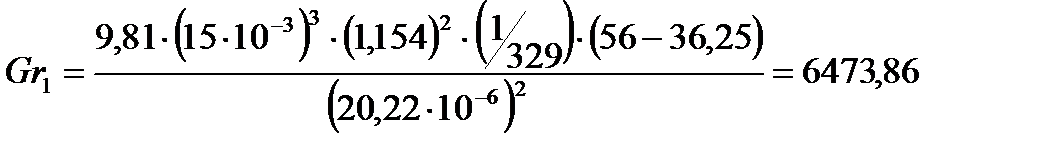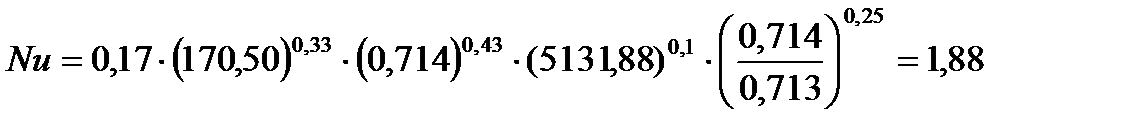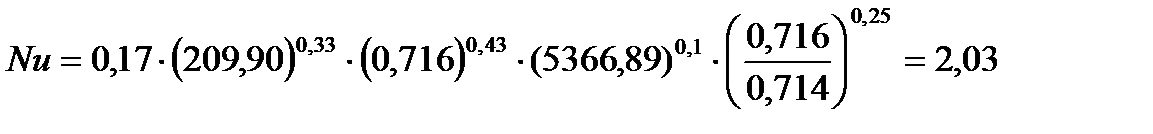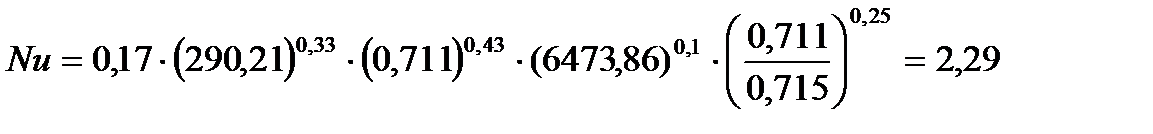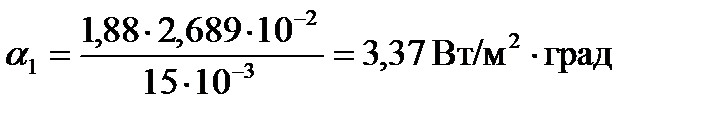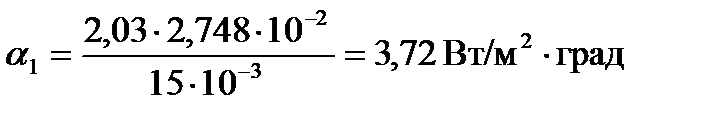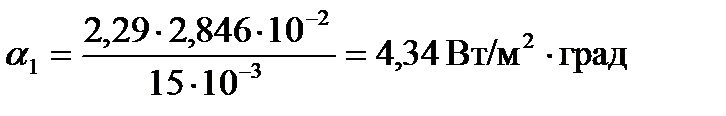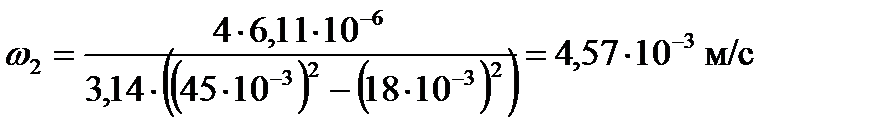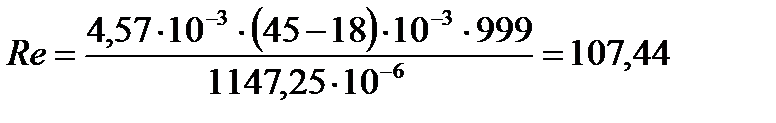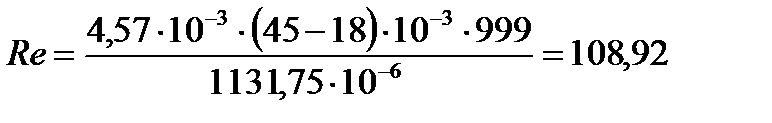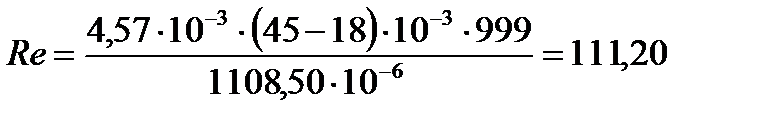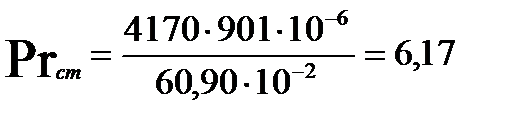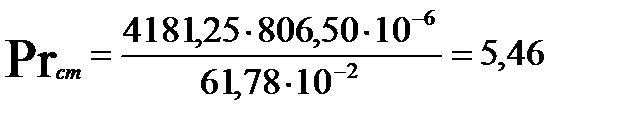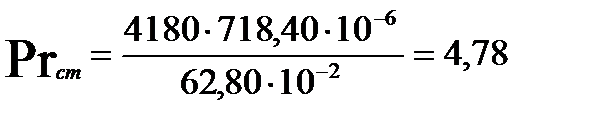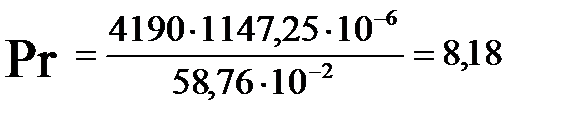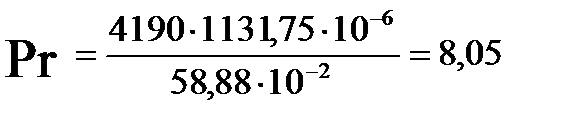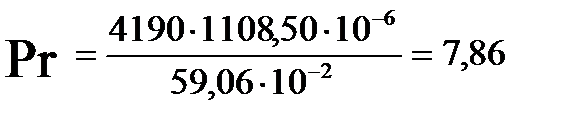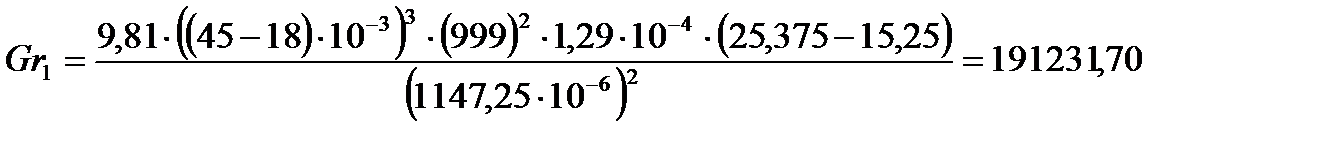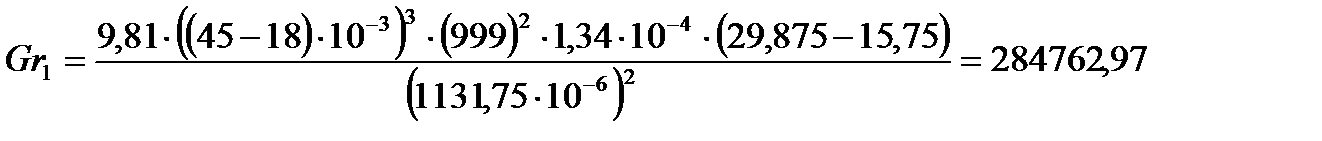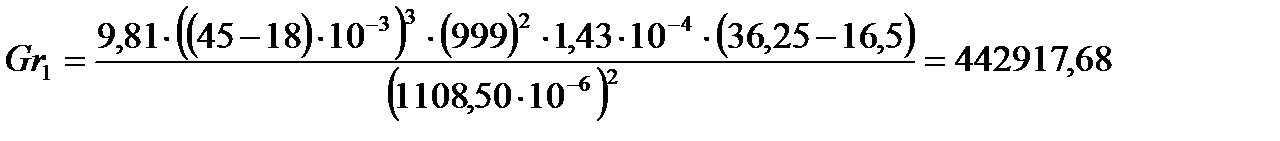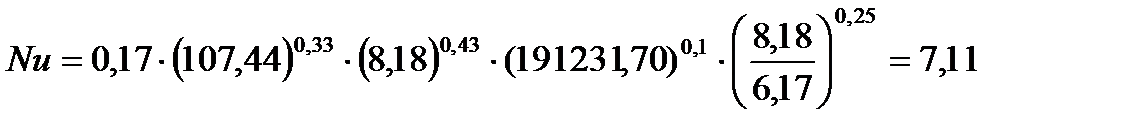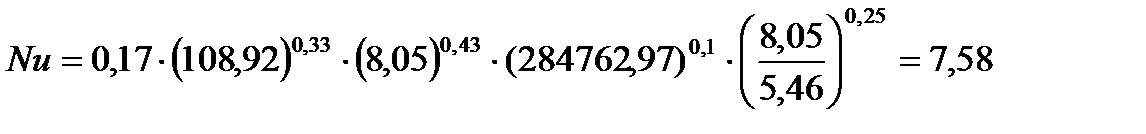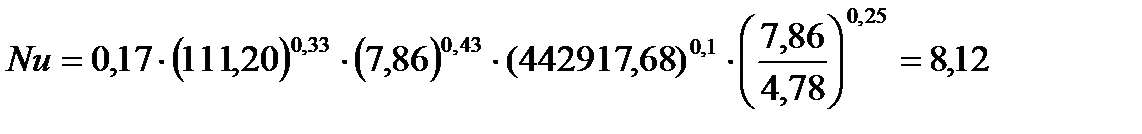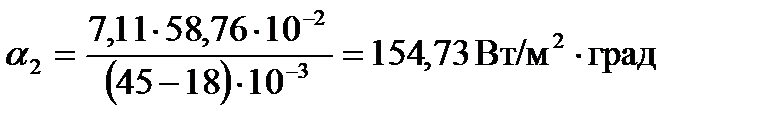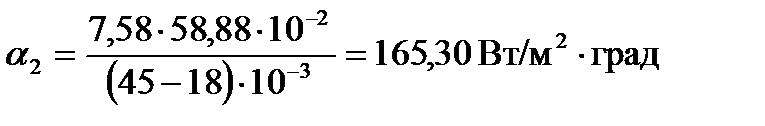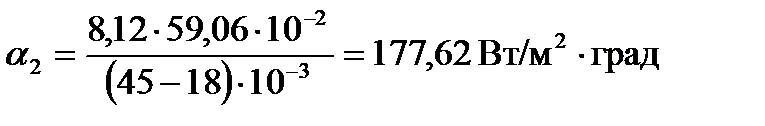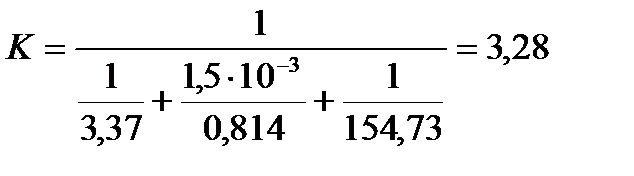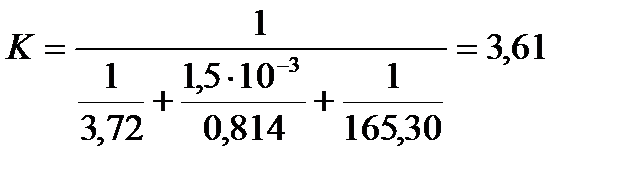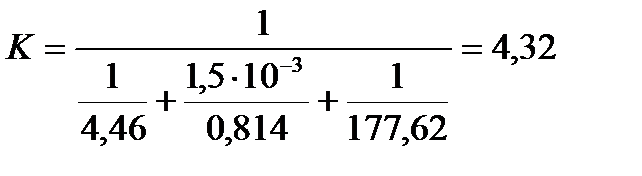в каком критерии физические параметры определены при температуре стенки
Определяющий размер и определяющая температура



В числа подобия входит определяющий (или характерный) размер. Теория подобия не определяет однозначно, какой размер должен быть принят за определяющий. Обычно за определяющий принимают тот размер, который в большей степени отвечает физическому существу процесса. При движении жидкости по трубам круглого сечения таким определяющим линейным размером является внутренний диаметр трубы. Тогда числа подобия запишутся так:
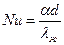
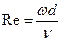
Для каналов некруглого сечения вместо диаметра берется так называемый эквивалентный диаметр:
При поперечном обтекании трубы или пучка труб за определяющий берется наружный диаметр трубы. При обтекании плиты ее длина по направлению потока и т.д.
В числа подобия входят физические параметры жидкости, которые зависят от температуры. В процессе теплообмена температура жидкости меняется следовательно, меняются и значения ее физических параметров. Поэтому важным является также вопрос выбора так называемой определяющей температуры, по которой определяются значения физических параметров, входящих в числа подобия. Экспериментальные и теоретические работы показывают, что нет такой универсальной определяющей температуры, в результате выбора которой автоматически учитывалась бы зависимость теплоотдачи в связи с изменением физических параметров. Поэтому в настоящее время преобладает точка зрения, в соответствии с которой за определяющую следует принимать такую температуру, которая в технических расчетах бывает задана или легко может быть вычислена.
В соответствии с этим при вынужденном движений жидкости в трубах и каналах, а также при вынужденном продольном и поперечном омывании пучков труб в качестве определяющей целесообразно принимать среднюю температуру потока жидкости.
При таком выборе определяющей температуры влияние резкого изменения значений физических параметров, в прилегающем к стенке пограничном слое, учитывается рассмотренным нами ранее сомножителем (Prж/Prст) 0.25
Следует помнить, что все числа подобия, входящие в уравнение подобия, должны быть взяты при одной определяющей температуре. Исключение составляет указанный выше сомножитель.
Определяющие размер и температура
Основные числа подобия. Формулы и физический смысл.
Критерии (числа) подобия
В теории конвективного теплообмена используются следующие числа подобия:
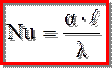
Nu представляет собой безразмерный коэффициент теплоотдачи и показывает отношение действительной плотности теплового потока к плотности теплового потока при чистой теплопроводности, т.е. Nu характеризует увеличение теплообмена конвекцией по сравнению с чистой теплопроводностью.
 |
Re представляет собой безразмерную скорость потока, характеризует гидродинамический режим потока. Re выражает отношение сил инерции (скоростного напора) к силам вязкого трения.
При малых числах Re преобладают силы вязкости, наблюдается упорядоченный спокойный ламинарный режим течения жидкости. При больших числах Re в потоке преобладают силы инерции, наблюдается вихревое турбулентное течение жидкости.
При течении жидкости в трубах:

Pr состоит из величин, характеризующих теплофизические свойства вещества и является теплофизической константой вещества.
Pr является мерой подобия скоростных и температурных полей в потоке. Для вязких жидкостей Pr > 1 и сильно зависит от температуры. Для газов величина Pr определяется атомностью:
— для одноатомных газов Pr = 0,67;
— для двухатомных газов Pr = 0,72;
— для трехатомных газов Pr = 0,80;
— для четырехатомных газов Pr = 1,0.
 |
Gr характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей. Этот критерий показывает влияние естественной конвекции на теплообмен.
Fo представляет собой безразмерное время и характеризует нестационарность процесса теплообмена.
Определяющие размер и температура
В числа подобия входит характерный линейный размер ℓ, называемый определяющим размером. За определяющий размер принимают тот, который входит в условия однозначности.
· для потока в круглой трубе: внутренний диаметр dвн ;
· при поперечном омывании трубы: наружный диаметр трубы dн:;
· при естественной конвекции: ширина b, длина ℓ, или высота h поверхности;
· при конвекции в ограниченном пространстве: ширина щели.
Определяющая температура – это температура, при которой определяются физические свойства жидкости в числах подобия.
При обработке опытных данных по теплообмену и гидравлическому сопротивлению за определяющую температуру целесообразно принимать такую, которая в технических расчетах бывает, задана или легко может быть определена.
· при конвекции в неограниченном пространстве: температура половинного слоя tm = 0,5 (tж + tc);
· при течении жидкости в трубе: температура стенки tc или средняя температура жидкости tж.
ТЕОРЕТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПЕРЕДАЧИ



1. Определим коэффициент теплоотдачи со стороны воздуха.
1.1 Определим скорость воздуха 
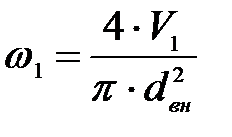
Подставляя числовые значения в формулу (6), получим:
опыт 1:
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 7.
1.2 Определим критерий Рейнольдса Re по формуле:
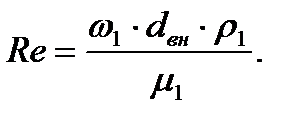
Подставляя числовые значения в формулу (7), получим:
опыт 1: 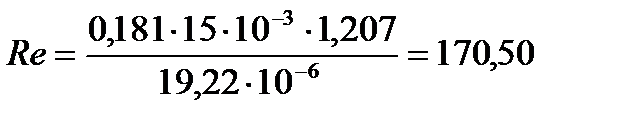
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 7.
1.3 Определим критерий Нуссельта Nu для ламинарного режима движения воздуха ( 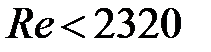
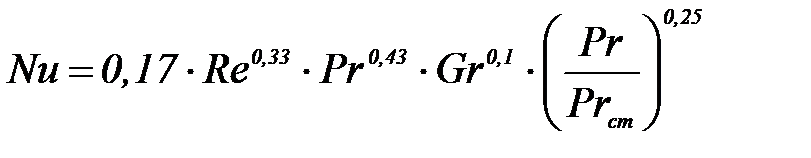
где Pr — критерий Прандтля, характеризующий физические свойства теплоносителя (определяется при средней температуре теплоносителя);
Gr — критерий Грасгофа, характеризующий влияние на теплоотдачу свободной конвекции;
Prст — критерий Прандтля, характеризующий физические свойства теплоносителя (определяется при температуре стенки 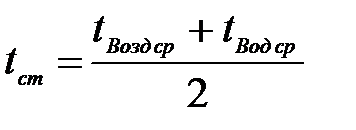
Определим по справочным данным числовые значения критерия Прандтля (при средней температуре воздуха) и сведем их в таблицу 5.
Определим среднюю температуру воды:
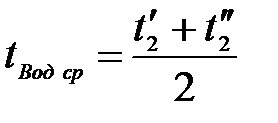
Подставляя числовые значения в формулу (9), получим:
опыт 1: 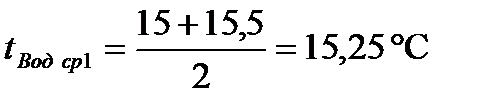
опыт 2: 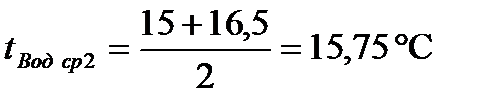
опыт 3: 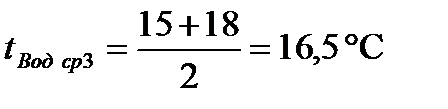
Результаты вычислений записали в таблицу 5.
На основе числовых значений средних температур воды и воздуха рассчитаем температуру стенки:
опыт 1: 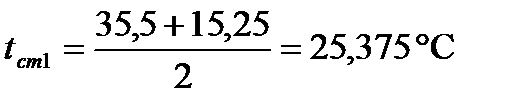
опыт 2: 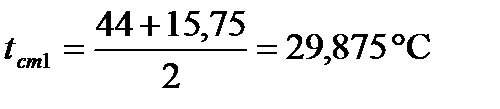
опыт 3:
Результаты вычислений записали в таблицу 6.
Определим критерий Прандтля (при температуре стенки):
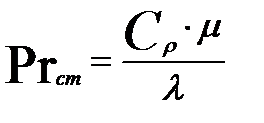
где: Cp — удельная теплоёмкость, Дж/(кг·град);
μ — коэффициент динамической вязкости, Па·с;
λ — коэффициент теплопроводности, Вт/(м·град).
опыт 1:
опыт 2:
опыт 2:
Результаты вычислений записали в таблицу 6.
Определим критерий Прандтля (при средней температуре):
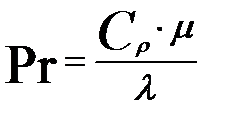
где: Cp — удельная теплоёмкость, Дж/(кг·град);
μ — коэффициент динамической вязкости, Па·с;
λ — коэффициент теплопроводности, Вт/(м·град).
опыт 1:
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 6.
Определим критерий Грасгофа по формуле:
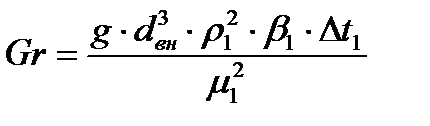
где 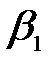
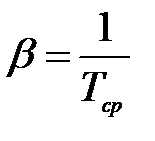
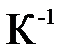
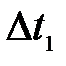
Подставляя числовые значения в формулу (11), получим:
опыт 1: 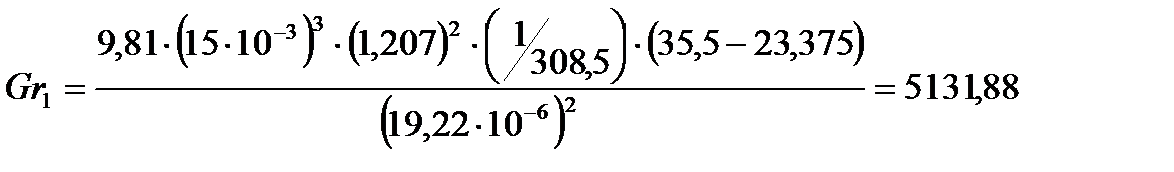
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 6.
Подставляя числовые значения в формулу (8), получим:
опыт 1:
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 7.
1.4 Определим коэффициент теплоотдачи со стороны воздуха по формуле:
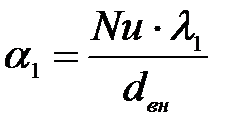
опыт 1:
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 7.
2. Определим коэффициент теплоотдачи со стороны воды.
Таблица 5 − Физические свойства воды.
Средняя температура 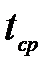 , , 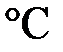 | Плотность 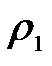 , кг/м 3 , кг/м 3 | Теплоемкость 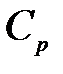 , , 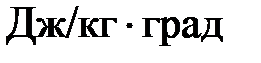 | Коэффициент динамической вязкости 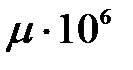 , , 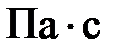 | Коэффициент теплопроводности 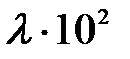 , , 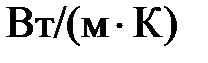 |
| 15,25 | 1147,25 | 58,76 | ||
| 15,75 | 1131,75 | 58,88 | ||
| 16,50 | 1108,50 | 59,06 |
2.1 Определим скорость воды 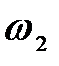
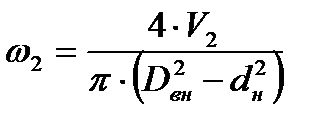
где: V2 — объёмный расход воды, м 3 /с;
Dвн — внутренний диаметр внешней трубы, м;
dн — наружний диаметр внутренней трубы, м.
Подставляя числовые значения в формулу (13), получим:
2.2 Определим критерий Рейнольдса Re по формуле:
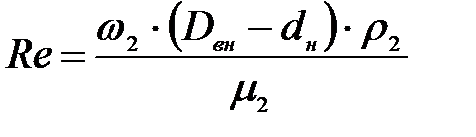
Подставляя числовые значения в формулу (14), получим:
опыт 1:
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 7.
2.3 Определим критерий Нуссельта Nu для ламинарного режима движения воды ( 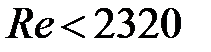
Определим критерий Прандтля (при температуре стенки):
где: Cp — удельная теплоёмкость, Дж/(кг·град);
μ — коэффициент динамической вязкости, Па·с;
λ — коэффициент теплопроводности, Вт/(м·град).
опыт 1:
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 6.
Определим критерий Прандтля (при средней температуре):
где: Cp — удельная теплоёмкость, Дж/(кг·град);
μ — коэффициент динамической вязкости, Па·с;
λ — коэффициент теплопроводности, Вт/(м·град).
опыт 1:
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 6.
Определим критерий Грасгофа по формуле:
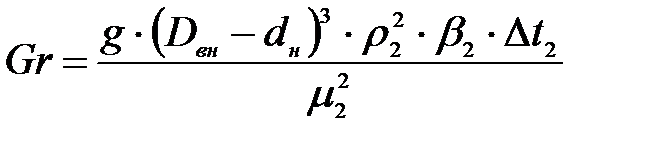
где 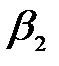
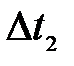
Подставляя числовые значения в формулу (11), получим:
опыт 1:
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 6.
Подставляя числовые значения в формулу (8), получим:
опыт 1:
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 7.
1.4 Определим коэффициент теплоотдачи со стороны воздуха по формуле:
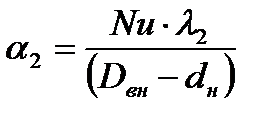
Подставляя числовые значения в формулу (15), получим:
опыт 1:
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 7.
Таблица 6 − Критерии подобия.
| № | Воздух | Вода | |||||
tcт,  | Pr | Gr | Prcт | tcт,  | Pr | Gr | Prcт |
| 25,375 | 0,714 | 5131,88 | 0,713 | 25,375 | 8,18 | 191231,70 | 6,17 |
| 29,875 | 0,716 | 5366,89 | 0,714 | 29,875 | 8,05 | 284762,97 | 5,46 |
| 36,25 | 0,711 | 6473,86 | 0,715 | 36,25 | 7,86 | 442917,68 | 4,78 |
Определим теоретический коэффициент теплопередачи по формуле:
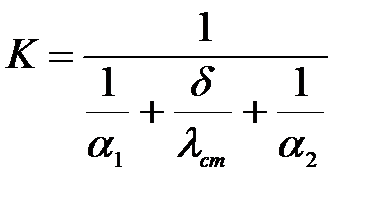
Подставляя числовые значения в формулу (17), получим:
опыт 1:
опыт 2:
опыт 3:
Результаты вычислений записали в таблицу 7.
Таблица 7 − Теоретический расчет коэффициента теплопередачи.
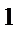
Рисунок 2. Зависимость коэффициента теплопередачи от скорости воздуха.
1 – теоретическая кривая; 2 ‒ опытная кривая.
Вывод: В ходе работы было изучено явление теплообмена между воздухом и водой. Были установлены теоретические и экспериментальные зависимости коэффициента теплопередачи от скорости воздушного потока. Выяснилось, что коэффициент теплопередачи при ламинарном режиме движения воздуха и воды возрастает почти прямо пропорционально скорости движения воздуха.