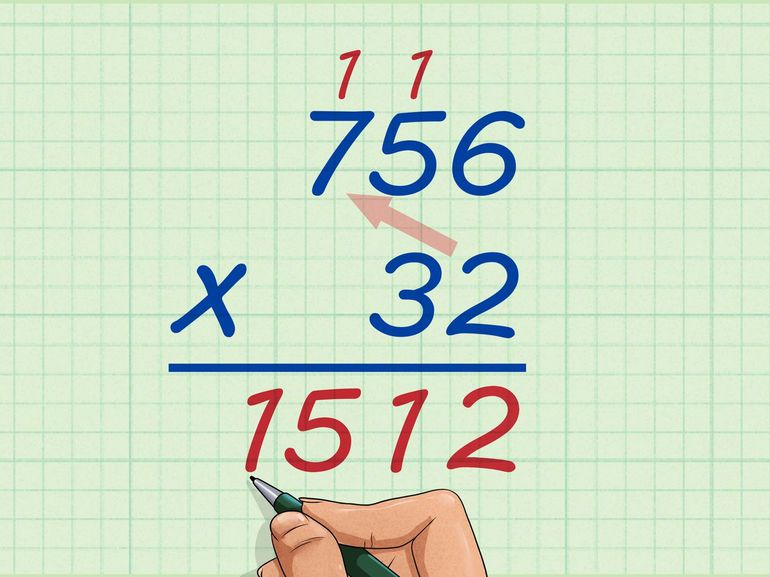в каком классе учат умножение в столбик
Математика. 5 класс
Конспект урока
Умножение чисел столбиком
Перечень вопросов, рассматриваемых в теме:
— умножение натуральных чисел столбиком;
— приёмы рационального вычисления многозначных чисел.
Умножение- арифметическое действие повторения данного числа слагаемым столько раз, сколько единиц находится в другом данном числе, множителе. Результат умножения- произведение.
Результат умножения на вторую цифру необходимо записывать под второй цифрой результата первого действия умножения.
Теоретический материал для самостоятельного изучения
Все знакомы с таблицей умножения: её используют для умножения однозначных чисел. Следует выучить её наизусть. Кроме того, надо помнить, что для любого натурального числа а верны равенства:
Вычисление произведения однозначного и многозначного чисел, и тем более двух многозначных чисел, требует применения не только таблицы умножения, но и законов сложения и умножения.
Можно представить число 723 в виде суммы разрядных слагаемых, и каждое из этих слагаемых умножить на 5, а затем сложить полученные результаты.
723 ∙ 5 = (700 + 20 + 3) ∙ 5 = 700 ∙ 5 + 20 ∙ 5 + 3 ∙ 5 = 3500 + 100 + 15 = 3615
А можно записать вычисление значения этого выражения столбиком:
При умножении трёх на пять получаем пятнадцать. Пять записываем в разряд единиц, единицу прибавляем в разряд десятков. При умножении двух на пять получаем десять, плюс единица, которую мы запомнили, получаем в разряде десятков единицу, единицу добавляем к разряду сотен. При умножении семи на пять получим тридцать пять, плюс один – тридцать шесть. Ответ: 3615.
Рассмотрим ещё одно выражение.
Запишем это произведение в столбик:
Сначала умножаем целиком верхнее число на последнюю цифру нижнего числа. Результат записываем под чертой под самой правой цифрой.
Умножаем число сверху по цифре (знаку) справа налево.
Переходим к умножению числа 329 на 3. Умножаем по тем же правилам, что и в предыдущем вычислении.
Результат умножения на вторую цифру необходимо записывать под второй цифрой результата первого действия умножения.
Полученные числа под чертой складываем по правилам сложения в столбик.
Рассмотрим такое выражение:
Чтобы найти значение этого выражения, не обязательно перемножать все числа в столбик: достаточно воспользоваться сочетательным законом умножения. Объединим попарно некоторые множители:
(25 ∙ 4) ∙ 589 ∙ (5 ∙ 2) ∙ (125 ∙ 8) = 100 ∙ 589 ∙ 10 ∙ 10000 = 589 ∙ 10000000 = 589000000
Разбор решения заданий тренировочного модуля
Решение: вычислим данное произведение в столбик:
№ 2. Пете ко Дню рождения надо было купить конфет. Он купил конфеты трёх видов: «Батончики», «Мишка на севере», «Грильяж». «Батончиков» он купил 56 штук, «Мишек на севере» – в 15 раз больше, чем «Батончиков», а «Грильяжа» на 50 конфет больше, чем «Батончиков». Сколько всего конфет купил Петя?
Варианты ответы: 1020, 1002, 1000, 992.
Урок математики в 4-м классе по теме «Как умножать многозначные числа столбиком»
Цели урока:
Замысел урока
Вопрос цикла
Место урока и его вопрос
Вид диалога на уроке
«Схема организации действия» по итогам урока
«Как умножать на многозначные числа?»
Конкретизация модели
«Как умножать на многозначные числа?
По какому алгоритму решаются любые примеры на умножение в столбик?»
(Алгоритм)
Диалог продуктивного действия.
Чтобы умножить многозначные числа в столбик, нужно:
1. Записать 2-й множитель под 1-м, соблюдая разряды.
2. Умножить единицы 2-го мн-ля на каждое разрядное слагаемое 1-го мн-ля, начиная с единиц.
3. Каждую разрядную единицу произведения записать в свой разряд.
4. Умножить 1-й мн-ль на число десятков 2-го мн-ля.
5. Каждую разрядную единицу произведения записать в свой разряд.
6. Сложить эти неполные произведения.
Ход урока
2.1. Первый и второй этапы дискуссии
Триада заданий:
СТАРТ-ЗАДАНИЕ
Сценарий исследующей дискуссии
Конкурирующие средства поиска детей
Запрос помощи учителем (фиксация ее получения)
Определенные детьми средства поиска
I. При выполнении задания и определении проблемы поиска
I. Проблема
— Почему не удалось быстро и правильно вычислить произведения двух последних примеров? В чём их особенность?
— У нас нет такого алгоритма, т.к. неизвестно, как умножать многозначное число на многозначное.
«–» алгоритм
II. Вопрос
«Как умножать на многозначные числа? По какому алгоритму решаются любые примеры на умножение в столбик?»
Реши и объясни, как ты это делал.

„–” не все неполные произведения вычислены

„–” нет разрядной записи неполных произведений

„–/+” Решил, показала приём мама.
— Итак, вы договорились, каким способом вычислить произведение при умножении многозначного числа на многозначное, чтобы получился одинаковый результат:
(Согласна, что не договорились.)
— Вы вычисляли эти примеры соблюдая разряды, посчитали все неполные произведения, не ошибались в вычислениях? Это помогло быстро и точно решить примеры?
(Действительно, не помогло.)
— А что помогло решить точно и быстро первые три примера? (Согласна, алгоритм.)
— Значит, алгоритм – для быстрого и точного решения-хорошо, но другой, в котором можно объяснить, как умножить многозначные числа вам еще не известен?
II. При определении вопроса поиска
— Как умножать на многозначные числа? По какому алгоритму решаются любые примеры на умножение в столбик?
— др. вопросы
— Тогда как будете двигаться дальше: повторно вычислять пример, или сначала разбираться в чем-то? (Действительно, надо разобраться.)
— Решите: в чем именно теперь вы намерены разобраться? (Ваши вопросы понятны)
— Раз вы все это хотите узнать, тогда нам нужен один общий вопрос! Скажите, какой? (Согласна, давайте в этом разбираться!)
Организация
Индивидуально (принцип индивидуальных вкладов), учитель-класс (обмен позициями)
2.2. Третий и четвертый этапы дискуссии
Триада заданий:
задание–эксперимент
Сценарий исследующей дискуссии
Конкурирующие средства поиска детей
Запрос помощи учителем (фиксация ее получения)
Определенные детьми средства поиска
III. При выдвижении гипотез об «открытии»
III. Гипотеза
1) Чтобы умножить многозначное число на 2-значное, надо разложить 2-мн-ль на разрядные слагаемые.
2) Найти неполные произведения.
3) Сложить неполные произведения и найти результат.
IV. Результат
Чтобы умножить многозначные числаможно:
1. Использовать решение в строку, где 2-й мн-ль разложен на разрядные слагаемые.
2. Грамотно вычислить и записать результат.
312х12=
312х10+312х2=
3120+624=3744
Поработайте в группе.
1) Запишите пример в строку и решите его.
2) Соотнесите запись в столбик с записью в строку
3) Выберите ту запись в строку, которая рассказывает почему так записывается решение в столбик и сделайте вывод.
Гипотезы про:
— На доске разные версии решения примера в строку. И какая же из них точно рассказывает о 1-м неполном произведении, о 2-м? (Поняла, тогда отредактируйте свои открытия те группы, у которых данные сравнения были не точными).
— Теперь из ваших версий не пойму, как же все-таки связаны 1-е и 2-е произведения? (Спасибо, понятно.)
— И на каком примере в строку вы окончательно остановитесь? (Хорошо, тогда снова отредактируйте свои открытия те группы, которых сейчас переубедили).
— Теперь есть ясность, как находятся произведения многозначных чисел? (Хорошо.)
IV. При определении результата поиска
Чтобы умножить многозначные числа можно:
1.Использовать решение в строку, где 2-й мн-ль разложен на разрядные слагаемые.
2. Грамотно вычислить и записать результат.
— др. версии
— Теперь скажите, пользуясь этим открытием, как действовать, чтобы найти произведения многозначных чисел. (Спасибо, все ваши предложения про порядок вычисления я записала на доске. Попробую так действовать)
312х12=
312х10+312х2=
3120+624=3744
(Нужно еще правильно произвести вычисления и записать результат).
— И какой порядок нахождения произведения получается, в итоге? (Теперь не ошибусь!)
Организация
По группам (обмен позициями), учитель-группы-класс (обмен позициями).
2.3. Пятый этап дискуссии
Триада заданий:
задание–эксперимент
Сценарий исследующей дискуссии
Конкурирующие средства поиска детей
Запрос помощи учителем (фиксация ее получения)
Определенное детьми средство поиска
V. При формулировке вывода как руководства к собственному действию
V. Вывод
(на «схеме организации действия» знаками + и –)
Чтобы умножить многозначные числа можно:
Использовать решение в строку, где 2-й мн-ль разложен на разрядные слагаемые.
2. Грамотно вычислить и записать результат.
— др. версии
— Cначала я разложил 2-й мн-ль на разрядные слагаемые. Затем умножил 1-й мн-ль на разрядное слагаемое. Получил неполные произведения. Сложил неполные произведения.
— Я работал так же, и у меня все получилось (отмечает + свои шаги на «схеме…»).
1) Запиши и реши пример в столбик, используя заданные выражения.
2) Объясни, как ты это сделал.
161х23=?
161х20=
161х3=
(на доске без обсуждения фиксируются только разногласия):
1) не смог (не понял)
— Каждый узнал новый способ умножения многозначных чисел. Но у кого-то получилось, а кто-то пока не смог умножить в столбик. Как же надо было действовать, чтобы выполнить это задание? (Спасибо, убедили, по-нашему порядку действий).
— Кому наш порядок действий сразу помог найти произведение, и каждый шаг пройден успешно? (Спасибо, вижу, отмечаю ваш ход работы знаками +).
— А у кого не получилось? (Спасибо, есть такие). Кто покажет на нашем «порядке действия», чему ему еще надо научиться? (Спасибо, если причина ясна, отредактируйте свои решения)
— Я вижу, что наш порядок действий теперь всем помог найти произведение.
Организация
Индивидуально (принцип индивидуальных вкладов), учитель-класс (обмен позициями).
Литература
Конспект урока «Умножение чисел столбиком»
Ищем педагогов в команду «Инфоурок»
Здравствуйте, ребята! Я рада снова встретиться с вами, даже в таком интересном формате работы! Надеюсь, что даже не в стенах школы мы продолжим плодотворно работать!
Поскольку рабочие тетради остались в школе, давайте с вами заведем одну тетрадочку, в которой вы и будете работать на протяжении всего обучения с применением электронного обучения. А в тех уже продолжим работу, когда вернемся в школу.
Умножение чисел столбиком
(Делаем запись в тетради, слово «Классная/домашняя работа не пишем)
Этот пример прост, поскольку нам достаточно умножить 5 на 4 (таблица умножения), а после к результату дописать два нуля.
Вспомните, я вам рассказывала «секрет», как просто умножать двузначные числа на 11. Способ первый. Умножай число на 10 и прибавляй к этому числу умножаемое число . Так, например, 38• 11 =38•10+38=418. Способ второй . Чтобы умножить любое двухзначное число на 11 , нужно сложить первую и последнюю цифры этого числа , а результат (сумму) вписать посередине (между первой и последней цифрами). Умножим на 11 число 15. Порядок действий следующий: Цифры 1 и 5 пишем с пробелом: 1_5. Складываем 1 и 5: 1 + 5 = 6. Цифру 6 вписываем между единичкой и пятеркой: получаем 165.
С какой проблемой мы столкнулись в этом примере?
Давайте для начала вспомним:
Как называют числа, которые перемножают?
Напомню, что буквами латинского алфавита мы можем «зашифровать» любое число. Это как-бы «ник-нейм» для числа, то есть как а, b или c – это могут быть абсолютно любые числа, так еще и хорошо вам известные х или у, и любые другие.
a и b – это __________________________________
с – это _____________________________________
Чему равно 1 • на любое число? __________________________
Чему равно 0 • на любое число? __________________________
(Делаем запись в тетради)
Вы все знакомы с таблицей умножения : её используют для умножения однозначных чисел. Следует выучить её наизусть, да, ведь мы с вами договаривались, что будете её повторять?
Давайте вместе повторим ее играя. Ниже есть несколько ссылок. Для того чтобы перейти по ним вы можете либо зажать клавишу Ctrl и кликнуть в этот момент мышью по ссылке, либо просто скопировать ее и вставить в строку браузера.
Получилось? Я уверена, что вы отлично справились!
Вычисление произведения однозначного и многозначного чисел, и тем более двух многозначных чисел, требует применения не только таблицы умножения, но и законов сложения и умножения.
Вычислим произведение 723 • 5 = _____
Можно представить число 723 в виде суммы разрядных слагаемых, и каждое из этих слагаемых умножить на 5, а затем сложить полученные результаты.
723 ∙ 5 = (700 + 20 + 3) ∙ 5 = 700 ∙ 5 + 20 ∙ 5 + 3 ∙ 5 = 3500 + 100 + 15 = 3615
(Делаем запись в тетради)
Давайте вспомним, как правильно это делать. Перейдите по ссылке, там вас ждет очень короткий, но очень понятный видеоролик: https://www.youtube.com/watch?v=W_dJLv8OIEA
Итак, вернемся к нашему примеру, запишем его в столбик.

При умножении трёх на пять получаем пятнадцать. Пять записываем в разряд единиц, единицу прибавляем в разряд десятков. При умножении двух на пять получаем десять, плюс единица, которую мы запомнили, получаем в разряде десятков единицу, единицу добавляем к разряду сотен. При умножении семи на пять получим тридцать пять, плюс один – тридцать шесть. Ответ: 3615.
(Делаем запись в тетради)
Рассмотрим ещё одно выражение.
Запишем это произведение в столбик:
Сначала умножаем целиком верхнее число на последнюю цифру нижнего числа. Результат записываем под чертой под самой правой цифрой.
Умножаем число сверху по цифре (знаку) справа налево.
Переходим к умножению числа 329 на 3. Умножаем по тем же правилам, что и в предыдущем вычислении.
Результат умножения на вторую цифру необходимо записывать под второй цифрой результата первого действия умножения.
Полученные числа под чертой складываем по правилам сложения в столбик.
(Делаем запись в тетради)
Задания, для самостоятельной тренировки своих навыков, вы найдете на сайте https://education.yandex.ru/main/
В поле «Вход для ученика» введите тот логин и пароль, который вам раздал классный руководитель.
Войдя в свой кабинет, вы обнаружите опубликованное мною занятие «30.10.2020».
Как умножать в столбик
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков.
Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.
Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.
Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.
Свойства умножения
1. От перестановки множителей местами произведение не меняется.
2. Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
Самое главное в процессе вычисления — это знание таблицы умножения. Это сделает подсчет упорядоченным и быстрым.
Важно помнить правило: умножение в столбик с нулями дает в результате ноль
Алгоритм умножения в столбик
Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:
1. Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.
2. Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения. Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д.
3. Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.
Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.
4. После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.
5. Складываем то, что нашли и получаем ответ.
Умножение на однозначное число
Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше.
Возьмем пример 234 * 2:
1. Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.
2. Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.
3. Ответ запишем под чертой:
Производить действия необходимо в следующей последовательности:
Умножение двух многозначных чисел
Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.
Рассмотрим пример 207 * 8063:
Ответ: 8 063 * 207 = 1669041.
Примеры на умножение в столбик
Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость. Неважно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем.
Вычислять же значения дробей и многозначных чисел в строку бывает довольно затруднительно.
удержать промежуточные результаты в голове порой просто невозможно. Как раз для таких случаев придумано умножение в столбик — этот метод значительно упрощает математические вычисления.
Необходимый минимум
Преимущество использования «столбиков» очевидно — пропадает необходимость считать в уме или всегда держать при себе калькулятор. Даже действительно длинные числа с помощью этого метода умножаются без лишних проблем. Достаточно иметь при себе:
Если же с последним пока ещё возникают затруднения, можно положить её рядом с собой и сверять по ходу решения. Правда, при таком раскладе процесс затянется на какое-то время, а полученный результат желательно перепроверить. Ведь одна маленькая ошибка в начале или середине вычисления сделает ответ заведомо неверным.
Регулярное решение примеров столбиком тренирует внимательность и память ребёнка, учит его концентрироваться на отдельно взятой задаче. Это также удобный способ закрепить базовые математические знания.
Как умножать столбиком
Чтобы научиться решать примеры, необходимо понять и отработать базовый алгоритм.
В целом он достаточно прост:
Метод столбиков не подходит для решения примеров, содержащих корни или возведённые в степень числа.
Прежде чем приступить к вычислениям, «проблемные» цифры нужно преобразовать до целых или десятичных.
Решение базовых примеров
Для большей наглядности стоит привести примеры умножения двузначных и трёхзначных чисел.
Пример 1 — отыскать произведение чисел 58 и 23. Решение задания:
По такому же принципу происходит умножение трёхзначных чисел. Разве что вычисление потребует чуть больше времени, а количество промежуточных результатов увеличится.
Пример 2 — решить выражение 659х854. Пошаговое решение:
При затруднениях в процессе решения можно проверить правильность умножения столбиком онлайн-калькулятором. А также существуют специальные генераторы примеров, которые используют как своеобразный тренажёр для закрепления изученного материала.
Целые числа с нулями
В ситуациях с нулями немного сложнее.
Если нолик «потерялся» где-то в середине, то в процессе решения его следует пропустить. Ведь умножение абсолютно любого числа на 0 в итоге даёт этот же 0. Поэтому можно сразу переходить к следующей цифре и заполнить строку под чертой, отступив не на 1, а на 2 единицы.
Что касается таких чисел как 10, 100, 1200, 12030 и т. п. — суть такая же, но алгоритм решения отличается. Вычисления проводят лишь с цифрами, отличными от нуля. А все «0» на конце чисел просто игнорируются. Хотя после сложения их количество надо подсчитать и добавить к ответу:
Задание 1 — найти произведение чисел 202 и 123. Решение таково:
Задание 2 — вычислить 120х300. Пошаговое решение:
Операции с десятичными дробями
На самом деле умножение десятичных дробей столбиком не слишком сильно отличается от аналогичного действия с числами, у которых есть нули.
В этом случае примеры решают точно так же, как и обычные — про запятую можно временно забыть. Но, когда ответ уже найден, её обязательно нужно восстановить. А для этого надо узнать, сколько цифр после запятой находится у каждого множителя. Их количество складывают, а потом отсчитывают это число с конца ответа.
Задание 1 — вычислить 2,5х3. Пошаговое решение:
Задание 2 — отыскать значение произведения 7,5х2,5. Решение с объяснением:
Если как следует разобраться в теме, юный математик сможет решать даже сложные примеры. Единственный минус метода — большие числа делают вычисления громоздкими, из-за каждой ошибки придётся проверять и править весь пример.