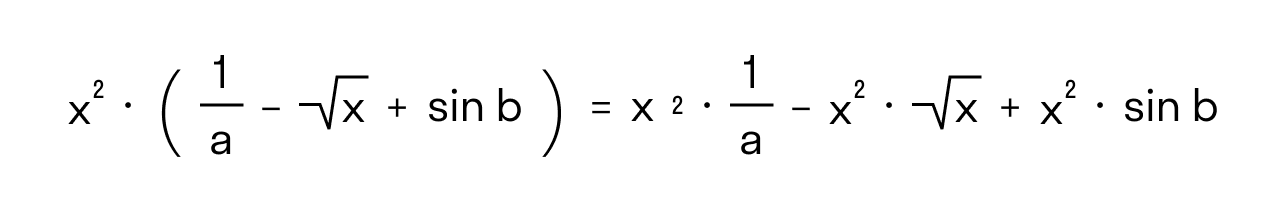в каком классе проходят раскрытие скобок

Математика. 6 класс

Раскрытие скобок и заключение в скобки

Преобразование выражений

Необходимо запомнить

Если сумма заключена в скобки, перед которыми стоит знак «+», то при раскрытии скобок знаки слагаемых оставляют без изменения.

Если сумма заключена в скобки, перед которыми стоит знак «–», то при раскрытии скобок знаки слагаемых меняют на противоположные.

Если сумма заключается в скобки, перед которыми стоит знак «+», то знаки слагаемых, заключаемых в скобки, оставляют без изменения.

Если сумма заключается в скобки, перед которыми стоит знак «–», то знаки слагаемых, заключаемых в скобки, меняют на противоположные.

Это интересно

Мы с вами изучили различные виды чисел. Вспомним, как они называются:

Помимо этих чисел есть ещё иррациональные, рациональные, действительные числа. О них мы узнаем позже, а сейчас мы рассмотрим совершенные и дружественные числа.

Совершенное число – это число, сумма собственных делителей которого (т. е. делителей, меньших самого числа) равна самому числу.

Наименьшие совершенные числа:

Сумма всех чисел, обратных делителям совершенного числа, включая его само, равна 2.

Поисками таких совершенных чисел занимались великие математики: Рене Декарт, Леонард Эйлер.

В настоящее время известно 46 совершенных чисел.

Пифагор говорил: «Мой друг тот, кто является моим вторым я, как числа 220 и 284».

Эти числа замечательны тем, что сумма делителей каждого из них равна второму числу. Такие числа были названы дружественными.

Любая пара дружественных чисел имеет одинаковую чётность. Взаимно простых дружественных чисел не существует.

На сегодняшний день известно более 1100 пар дружественных чисел, найденных или подбором вручную, или перебором на компьютере.

Источник

Урок математики по теме «Раскрытие скобок». 6-й класс

Разделы: Математика

Класс: 6

Тип урока: урок изучения нового материала.

I. Организационный момент.

Проверь-ка дружок
Ты готов на урок?
Всё ли на месте? Всё в порядке?
Ручка, книжка и тетрадка.
Все ли правильно сидят?
Все ль внимательно глядят?

Начать урок я хочу с вопроса к вам:

Как вы думаете, что самое ценное на Земле? (Ответы детей.)

Этот вопрос волновал человечество не одну тысячу лет. Вот какой ответ дал известный ученый Аль-Бируни : “Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит”.

Пусть эти слова станут девизом нашего урока.

II. Актуализация прежних знаний, умений, навыков:

1.1. Какое сегодня число?

2. Расскажите, что вы знаете о числе 20?

3. А где расположено это число на координатной прямой?

4. Назовите число ему обратное.

5. Назовите число ему противоположное.

6. Как называется число – 20?

7. Какие числа называются противоположными?

8. Какие числа называются отрицательными?

9. Чем равен модуль числа 20? – 20?

10. Чему равна сумма противоположных чисел?

2. Объясните следующие записи:

а) Гениальный математик древности Архимед родился в 0 287 г.

б) Гениальный русский математик Н.И.Лобаческий родился в 1792 г.

в) Первые олимпийские игры состоялись в Греции в – 776 г.

г) Первые Международные олимпийские игры состоялись в 1896 г.

д) XXII Олимпийские зимние игры состоялись в 2014 году.

3. Узнайте, какие числа крутятся на “математической карусели” (все действия выполняются устно).

II. Формирование новых знаний, умений, навыков.

Вы научились выполнять разные действия с целыми числами. Чем же будем заниматься дальше? Как будем решать примеры и уравнения?

Давайте найдем значение данных выражений

Какой порядок действий в 1 примере? Сколько получилось в скобках? Порядок действий во втором примере? Результат первого действия? Что можно сказать об этих выражениях?

Что же мы сделали со скобками? (Опустили.)

Как вы думаете чем мы будем заниматься сегодня на уроке? (Дети формулируют тему урока.) В нашем примере, какой знак стоит перед скобками. (Плюс.)

И так мы подошли к следующему правилу:

Если перед скобками стоит знак +, то можно опустить скобки и этот знак +, сохраняя знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком +.

А как быть, если перед скобками стоит знак минус?

В этом случае нужно рассуждать так же как при вычитании: необходимо прибавить число противоположное вычитаемому:

– Итак, мы раскрыли скобки, когда перед ними стоял знак минус.

Правило раскрытия скобок, когда перед скобками стоит знак “-“.

Давайте послушаем правила раскрытия скобок в стихах:

Перед скобкой плюс стоит.
Он о том и говорит
Что ты скобки опускай
Да все знаки выпускай!
Перед скобкой минус строгий
Загородит нам дорогу
Чтобы скобки убирать
Надо знаки поменять!

Да ребята знак минус очень коварный, это “ сторож” у ворот(скобки), он выпускает числа и переменные только тогда, когда они поменяют “ паспорта”, то есть свои знаки.

Зачем вообще нужно раскрывать скобки? (Когда есть скобки, есть момент какой-то элемент незавершенности, какой-то тайны. Это – как закрытая дверь, за которой находится что-то интересное.) Вот сегодня мы изведали эту тайну.

Небольшой экскурс в историю:

Фигурные скобки появляются в сочинениях Виета (1593). Широкое применение скобки получили лишь в первой половине XVIII века, благодаря Лейбницу и ещё больше Эйлеру.

III. Закрепление новых знаний, умений, навыков.

Работа по учебнику:

№ 1234 (раскройте скобки) – устно.

№ 1236(раскройте скобки) – устно.

№ 1235 (найдите значение выражения) – письменно.

№ 1238 (упростите выражения) – работа в парах.

IV. Подведение итогов урока.

1. Объявляются оценки.

3. Чему мы сегодня научились?

И завершить урок я хочу пожеланиями каждому из вас:

“К математике способность проявляй,
Не ленись, а ежедневно развивай.
Умножай, дели, трудись, соображай,
С математикой дружить не забывай”.

Источник

Математика. 6 класс

Конспект урока

Раскрытие скобок и заключение в скобки

Перечень рассматриваемых вопросов:

Целые числа – это натуральные числа, ноль и числа противоположные натуральным.

Противоположные числа – это числа, которые отличаются только знаком и при сложении друг с другом в сумме дают 0. Число 0 противоположно самому себе.

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Сегодня мы продолжим рассматривать распределительный закон в двух случаях: раскрытие скобок и заключение слагаемых в скобки.

Такое выражение, как 4 – 9 – 2, часто называют суммой, потому что его можно записать в виде суммы 4 + (– 9) + (– 2).

Вспомним действия сложения и вычитания целых чисел, а также узнаем, какие ещё виды чисел существуют.

Сформулируем правило раскрытия скобок, перед которыми стоит знак «плюс».

Если сумма заключена в скобки, передкоторыми стоит знак «плюс», то при раскрытиискобок знаки слагаемых оставляют без изменения.

Пользуясь этим правилом, выполним раскрытие скобок

+ (25 – 12 + 6) = 25 – 12 + 6

+ (– 31 + 29 – 15) = – 31 + 29 – 15

Сформулируем правило раскрытия скобок, перед которыми стоит знак «минус».

Если сумма заключена в скобки, перед которыми стоит знак минус, то при раскрытии скобок знаки слагаемых меняют на противоположные.

– (а – b – с) = – а + b + с

Применим это правило при раскрытии скобок, перед которыми стоит «минус».

– (22 – 30 +19)= – 22 + 30 – 19

Теперь сформулируем правило заключения в скобки, когда пред скобкой стоит «плюс».

Если сумма заключается в скобки, передкоторыми стоит знак «+», то знаки слагаемых,заключаемых в скобки, оставляют безизменения.

– а + b – с = + (– а + b – с)

Рассмотрим числовое выражение и заключим его в скобки, поставив перед скобкой «плюс».

– 4 + 9 – 5 = + (– 4 + 9 – 5)

Сформулируем правило заключения в скобки, перед которыми будет стоять знак «минус».

Если сумма заключается в скобки, перед которыми стоит знак «–», то знаки слагаемых,заключаемых в скобки, меняют напротивоположные.

а– b + с – d = – (– a + b – c + d)

Посмотрим на примере числового выражения, как происходит заключение в скобки.

123 – 25 + 37= – (– 123 + 25 – 37)

Найдите значение выражения:

Упростим числовое выражение, применяя рассмотренные ранее правила.

– (620 – 29) + 31= – 620 + 29 + 31= – 620 + (29 + 31) =

Найдите значение выражения:

Снова упростим числовое выражение.

(8 ∙ 75 – 600) – 8 ∙ 75 = 8 ∙ 75 – 600 – 8 ∙ 75 =

= 8 ∙ 75 + (– 600) + (– 8 ∙ 75) = 8 ∙ 75 + (– 8 ∙ 75) + (– 600) =

= (8 ∙ 75 + (– 8 ∙ 75)) + (– 600) = (8 ∙ 75 – 8 ∙ 75) – 600 =

= 8 ∙ (75 – 75) – 600 =8 ∙ 0– 600 = 0 – 600 = – 600

Таким образом, на этом уроке мы сформулировали правила раскрытия скобок, перед которыми стоит знак «+» или знак «–», сформулировали правила заключения слагаемых в скобки.

Научилисьупрощать числовые выражения, применяя правила раскрытия скобоки правила заключения слагаемых в скобки.

Мы изучили с вами различные виды чисел. Вспомним, как они называются:

Источник

Раскрытие скобок

Понятие раскрытия скобок

В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.

Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.

Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:

Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.

Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.

В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:

Раскрытие скобок также можно рассматривать шире.

Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:

Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:

Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.

Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:

Первое правило раскрытия скобок

Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.

Первое правило раскрытия скобок

Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак.

Формула раскрытия скобок

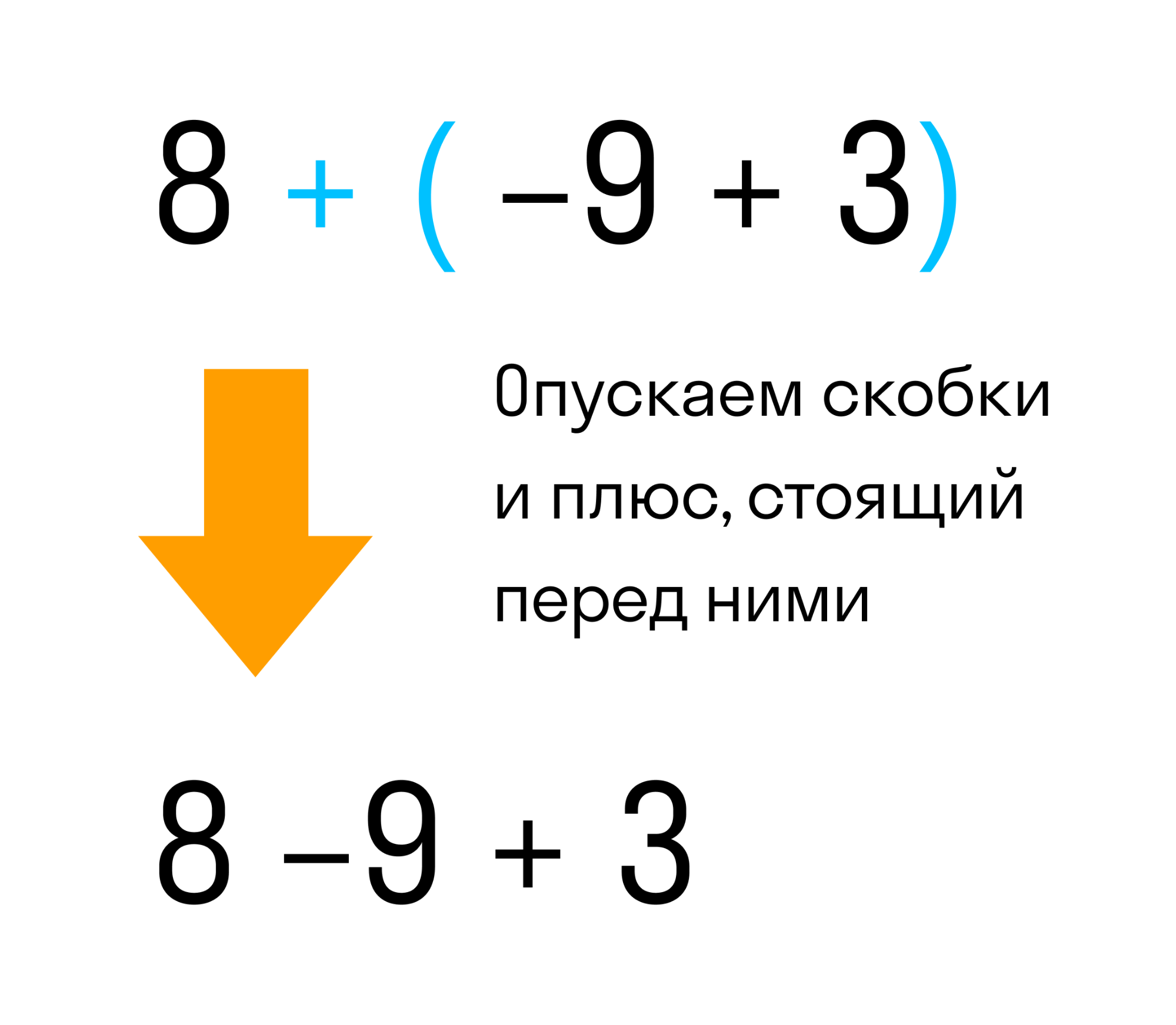
Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:

Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.

Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

Потренируемся применять правило на примерах.

Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)

Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:

Пример 2. Раскрыть скобки в выражении 6 + (−2)

Перед скобками стоит плюс, значит применим то же правило:

Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.

В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.

Идем дальше. Теперь упростим выражение 2a + a − 5b + b.

Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.

Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.

После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:

Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:

Пример 3. Раскрыть скобки 6 + (−3) + (−2)

В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:

Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.

Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.

Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

Пример 4. Раскрыть скобки в выражении (−7)

Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:

Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)

Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:

Второе правило раскрытия скобок

Здесь рассмотрим второе правило раскрытия скобок. Звучит так:

Второе правило раскрытия скобок

Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.

Формула раскрытия скобок

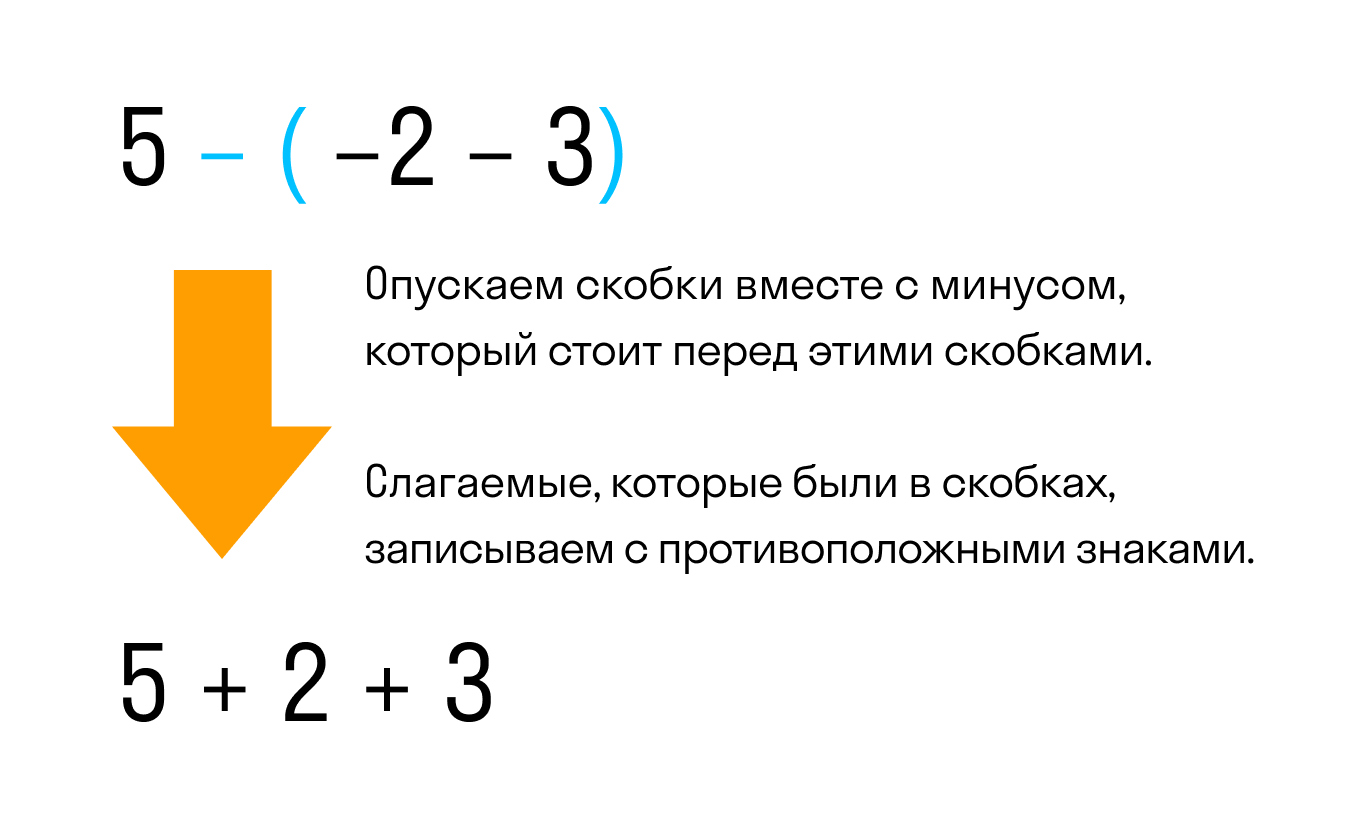
Например, раскроем скобки в выражении 5 − (−2 − 3)

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.

Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:

Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

Пример 2. Раскрыть скобки −(−6 + 7)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)

Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:

−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2

Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

a − (3b + 3) + 10 = a − 3b − 3 + 10

Другие правила раскрытия скобок

Правило раскрытия скобок при делении

Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок.

Формула раскрытия скобок

Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.

Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.

Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:

Далее умножим скобку на число:

Правило раскрытия скобок при умножении:

Если перед скобками стоит знак умножения — каждое число, которое стоит внутри скобок, нужно умножить на множитель перед скобками.

Формула раскрытия скобок

Пример 1. Раскрыть скобки 5(3 − x)

В скобке у нас стоят 3 и −x, а перед скобкой — пятерка. Значит, каждый член скобки нужно умножить на 5:

Знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

Пример 2. Упростить выражение: 5(x + y) − 2(x − y)

Как решаем: 5(x + y) − 2(x − y) = 5x + 5y − 2x + 2y = 3x + 7y.

Таблица с формулами раскрытия скобок

Эти таблицы с правилами раскрытия скобок можно распечатать и обращаться к ним, когда возникнут сомнения в ходе решения задачки.

Правила раскрытия круглых скобок вида (-a), в которых находится одночлен

Правила раскрытия круглых скобок, в которых находится многочлен

Скобки убирают, знаки всех слагаемых в скобках не меняют, если:

Скобки убирают, знаки всех слагаемых в скобках меняются на противоположные, если:

Раскрытие круглых скобок при умножении одночлена на многочлен

Раскрытие круглых скобок при умножении многочлена на многочлен

Раскрытие круглых скобок при возведении многочлена в степень

(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b)= a2 + ab + ab + b2 = a2 + 2ab + b2

Скобка в скобке

В 7 классе на алгебре можно встретить задачи со скобками, которые вложены внутрь других скобок. Вот пример такого задания:

Чтобы успешно решать подобные задания, нужно:

При этом важно при раскрытии одной из скобок не трогать все остальное выражение и просто переписывать его, как есть. Разберем подробнее тот же самый пример.

Пример 1. Раскрыть скобки и привести подобные слагаемые 7x + 2(5 − (3x + y))

Начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относится – это сама скобка и минус перед ней. Всё остальное переписываем также как было.

Теперь раскроем вторую скобку, внешнюю:

Упростим получившееся выражение:

Порядок раскрытия скобок

Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида. То есть в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.

Порядок раскрытия скобок согласован с порядком выполнения действий:

Пример 1. Раскрыть скобки и упростить выражение:

Значение выражения не зависит от переменной и всегда отрицательно. Что и требовалось доказать.

Задачи для самостоятельного решения

На алгебре в 6 и 7 классе придется решать задачки с раскрытием скобок много и часто. Поэтому лучше запомнить правила и практиковаться уже сейчас.

Задание 6. Раскройте скобки:

Задание 7. Раскройте скобки:

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Конспект урока по математике на тему «Раскрытие скобок» (6 класс)

Ищем педагогов в команду «Инфоурок»

Учебный предмет : математика

Класс : 6 А, 22.12.2015

Тема урока : Раскрытие скобок.

Тип урока: Урок открытия новых знаний.

Цель урока: формировать навык раскрытия скобок при упрощении выражений (на данном уроке – это ключевое УУД, системообразующее по отношению к другим УУД урока). Создание условий для систематизации, обобщения и углубления знаний учащихся при решении упражнений по теме «Действия с рациональными числами»

— формировать способность к раскрытию скобок с учётом знака, стоящего перед скобками (познавательные УУД);

— определить готовность учащихся к самостоятельному выполнению заданий на решение задач различного вида по теме «Раскрытие скобок» (познавательные УУД).

— закрепить вычислительные навыки при работе с положительными и отрицательными числами; (познавательные УУД).

— способствовать развитию у учащихся УУД (регулятивного) самоопределения в целях учебной деятельности (на основе установления сходства и различия между освоенным ранее и осваиваемым на данном уроке);

— способствовать развитию у учащихся УУД (познавательного) поиска и распознавания полезной информации (на основе наблюдения и оценки выявленных закономерностей).

— способствовать развитию у учащихся УУД (регулятивного) самоконтроля учебной деятельности (на основе сравнения способа действия и его результата с заданным эталоном).

— способствовать развитию у учащихся УУД (коммуникативного) оценивания ситуаций взаимодействия в соответствии с правилами поведения и этики.

— способствовать развитию у учащихся УУД (личностного) осознания осваиваемого на уроке приема учебной деятельности, как ценности.

Методы и формы обучения: Фронтальная, парная, индивидуальная, групповая

1. Мотивация к учебной деятельности

2. Актуализация опорных знаний. (Устный счет)

3. Изучение нового материала.

4. Первичное закрепление изученного материала с проговариванием во внешней речи.

6. Закрепление изученного материала.

7. Обобщающая самостоятельная работа

8. Итоги урока. Домашние задание.

1. Мотивация к учебной деятельности

Учитель: Добрый день, дорогие ребята! С каким настроением вы пришли на урок математики?

Давайте сейчас улыбнемся друг другу и пожелаем хорошего настроения!

Поприветствуем наших гостей.

-Начать урок мне хотелось бы со слов

— чтобы быстро и верно считать, поработаем устно.

2. Актуализация опорных знаний

Устный счет и фронтальный опрос

Вспомним пройденный материал.

— как мы находим сумму где оба слагаемых имеют одинаковые знаки?

— как мы находим сумму где оба слагаемых имеют разные знаки?

— как умножить и разделить два числа с разными знаками?

— как умножить и разделить два числа с одинаковыми знаками?

3 b +7 d +6 d =3 b +13 d

3. Изучение нового материала.

Учитель: С каким затруднением вы столкнулись при выполнении этого задания?

Как вы думаете почему?

Учитель : Значит, чем мы будем заниматься? Попробуйте сформулировать тему урока.

Дети: «Раскрытие скобок » (Открываю на доске тему)

Учитель: Правильно. Итак, мы с вами начинаем изучать большой раздел Преобразование буквенных выражений.

И первая тема из этого раздела, «Раскрытие скобок».

Какие цели и задачи мы поставим на урок?

1) научиться раскрывать скобки, перед которыми стоит знак «+» или «-»;

2) применять полученные знания при выполнении различных заданий;

3) научиться применять правило раскрытия скобок при упрощении выражений.

Открываем тетрадь, записываем число классная работа, и тему урока.

Учитель: А где мы можем найти правила раскрытия скобок?

учитель: Итак, какое же правило раскрытия скобок, перед которыми стоит знак «+», можно сформулировать? (одного прошу прочитать вслух)

Если перед скобками стоит знак +, это значит, что все слагаемые в скобках надо умножить на 1, т.е., раскрывая скобки, оставить их без изменения.

А если, ребята, перед скобкой нет никакого знака, то мы считаем, что перед ней стоит «+»

учитель: А теперь найдем правило раскрытия скобок, перед которыми стоит знак «-»?(одного прошу прочитать вслух)

А сейчас, давайте отгадаем загадки

Если перед скобкой плюс,

Просто скобки опускаю,

Ну а знаки. (сохраняю).

Если перед скобкой минус,

То мозгами пораскину.

Скобки тоже опускаю,

Ну а знаки. (поменяю).

Работа с учебником. С проговариванием во внешней речи.

а) делаю сама у доски

б,в,г вызываю по одному к доске, с проговариванием во внешней речи

— Я предлагаю вам немного отдохнуть, но не забывать о теме нашего урока. Я вам буду показывать выражение с заданием и ответ,

если ответ правильный – вы встаёте на носочки и поднимаете руки вверх,

если вообще не можете никак ответить-то поворачиваете головой влево и вправо.

А сейчас давайте выполним несколько упражнений.

6-(к+ d )=6- k + d неверно

6. Закрепление изученного материала.

Работа в парах – математическое лото

Необходимо правильно совместить 2 карточки, решение записываем в тетрадь

= = 1

Учащиеся в паре выполняют решение предложенных заданий и сравнивают его с эталоном.

Работа в группах (проверка с эталоном)

Задание 1. Раскройте скобки и найдите значение выражения

Задание 2. Упростите выражение. С помощью таблицы найдите зашифрованное слово:

— С помощью таблицы найдите зашифрованное слово:

Источник