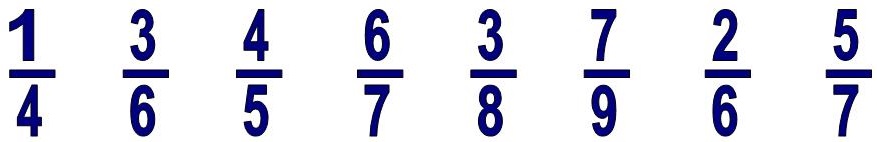в каком классе проходят обыкновенные дроби
Дроби и доли.
Дроби самая сложная тема для учеников начальных классов. Но даже самая трудная тема может стать простой и понятной. Для обучения детей нужно использовать фантазию и элементы игры. А главное – сохранять спокойствие.
В серьезных учебниках по математике есть знаки: и сложение, и вычитание, и умножение. А вот, привычного нам, с вами знака деления (:) – нет. Получается, что знаком деления (:) пользуются только ученики начальной школы? На самом деле – нет. Только этот знак можно писать и по-другому, вот такой чертой, она пишется посередине клетки:
Вот это все – деление.
Деление можно записывать не двумя точками, а горизонтальной полоской.
Так вот: любая математическая запись, в которой присутствует знак деления в виде черточки, называется дробью.
Слово «дробь» говорит само за себя – оно обозначает дробление или деление.
Для записи дробей используются цифры и черта, которую называют дробной.
Вы когда-нибудь видели военный парад? Идут солдаты стройными рядами, а впереди человек со знаменем (флагом) – знаменосец! И по знамени легко понять, к какому роду войск принадлежат эти солдаты. У дроби тоже есть «знаменосец» — это главное число, которое обозначает, на сколько равных частей разделили целое (предмет, фигуру или величину).
«Знаменосец» пишется под дробной чертой и называется ЗНАМЕНАТЕЛЬ.
А число, над чертой показывает, сколько таких частей взяли (или закрасили, или съели). Это число называют ЧИСЛИТЕЛЕМ.
читается – две третьих, можно заменить по-другому — 2 : 3.
Рассмотрим еще одно число: раньше мы не могли на уроке математики 1 разделить на 2. А теперь – умеем: 1 разделить на 2 – это не что иное, как одна вторая. Что же это значит? Если в математике мы с вами не делали этого ни разу, то в жизни вы это делаем постоянно. Предположим, у вас есть яблоко. И вам нужно разделить его между вами и другом. Т.е. одно яблоко разделить на 2.
Так что же за число такое – одна вторая, во-первых, это дробь потому что присутствует знак деления, во-вторых, оно меньше единицы.
Потому что нельзя один разделить на 2, чтобы получилось что-то больше 1.
В-третьих, оно обозначает, что мы целое разделили на 2 и взяли себе одну такую часть.
Давайте посмотрим на число:
По правилу, которое мы с вами вывели: три четвертых – это тоже самое, что три разделить на 4.
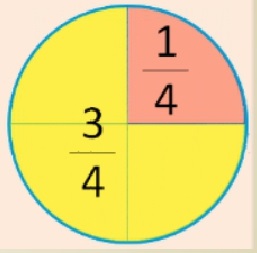
Давайте посмотрим, как это понять. Круг разделим на 4 равные части.
3 части закрасим желтым цветом. Это и есть три четвертых. Что же это значит?
Во-первых, это тоже дробь.
Во-вторых, она тоже меньше единицы.
И она обозначает, что круг мы разделили на 4 части
и закрасили желтым цветом – 3 таких части.
Итак,
как вы уже поняли: любая дробь будет иметь черту.
Ее так и называют – дробная черта. И обязательно будет стоять какое-то число над чертой и какое-то число под чертой.
Давайте научимся, как правильно читать дроби.
Читают их так: верхнее число всегда будет отвечать на вопрос: сколько?, а нижнее будет отвечать на вопрос: какая? или каких?
Сколько? – три, каких? – восьмых – три восьмых,
Сколько? – семь, каких? – девятых – семь девятых,
Сколько? – две, каких? – шестых – две шестых,
Сколько? – пять, каких? – седьмых – пять седьмых.
У чисел, которые вверху и внизу дроби есть свое научное название: верхнее число называется числитель, а нижнее – знаменатель.
Постарайтесь запомнить это. Это важно! Числитель – наверху, знаменатель – внизу.
Знаменатель показывает на сколько частей мы разделили наше целое, а числитель показывает – сколько частей целого мы с вами взяли.
Чтобы лучше запомнить, где числитель, где знаменатель, есть простая напоминалочка:
«ЧЕЛОВЕК ХОДИТ ПО ЗЕМЛЕ».
Ч – числитель – «над», З – знаменатель «под».
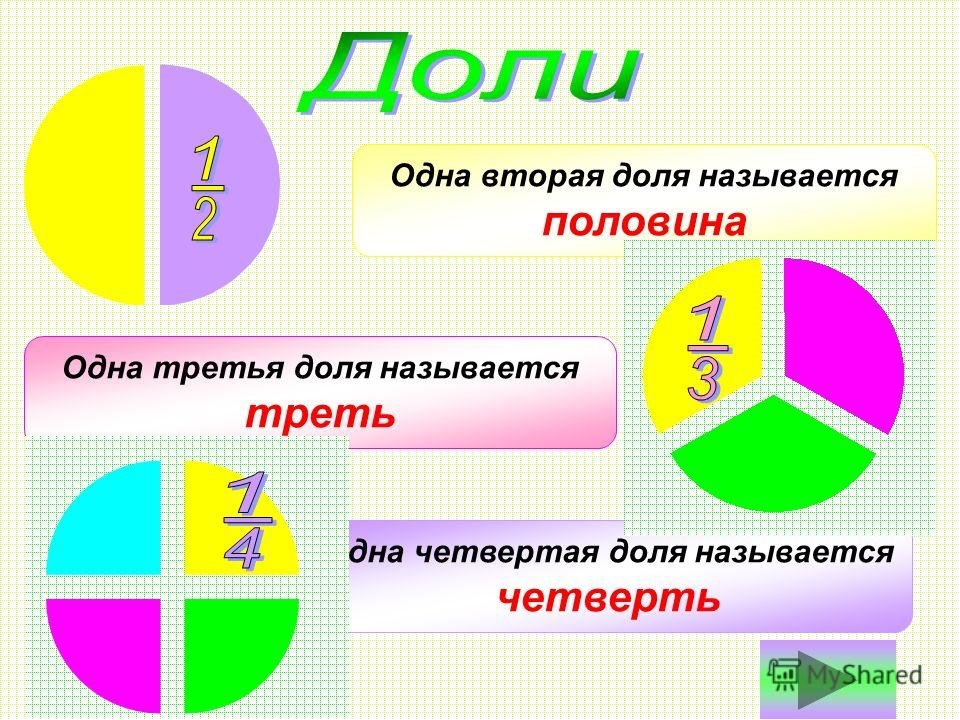
Есть одна разновидность дробей, которую в начальной школе выделяют в отдельную группу. Такие дроби называют долями. Если вам встретилось слово «доля», знайте, что это та же самая дробь, но только у нее числитель равен единице.
Мы постоянно сталкиваемся с ними в жизни.
Чаще всего мы встречаемся в жизни именно с половиной:
пол яблока — это одна вторая яблока, пол стакана – это одна вторая стакана.
Так же мы знакомы с одной третьей:
– это не что иное, как треть.
Треть грейфрута – это значит, разделили грейфрут на 3 части и взяли одну.
Точно так же мы с вами называем одну четвертую четвертью.
Например – школьная четверть. Мы с вами делим учебный год на 4 части и берем одну часть. Это и есть – четверть.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.9 / 5. Количество оценок: 78
Математика. 5 класс
Конспект урока
Перечень рассматриваемых вопросов:
Дробь в математике – число, состоящее из одной или нескольких равных частей (долей) единицы.
Правильные дроби – это дроби, в которых числитель меньше знаменателя
Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя.
Теоретический материал для самостоятельного изучения
Очень часто в жизни мы слышим такие выражения: «Прошел половину пути», «Купил четвертинку хлеба», «Сделал третью часть от работы». Все эти выражения связаны с новым понятием «дробь». О ней сегодня и пойдёт речь.
Чтобы ввести понятие дроби, выполним следующее задание.
Две части будут весить две третьих килограмма.
Если на отрезке АС укладывается ровно 3 раза отрезок длиной одна пятая сантиметра, то говорят, что длина отрезка равна три пятых сантиметра.
Такие записи называются обыкновенными дробями или просто дробями.
Дробь показывает какую-то часть от целого или единицы. Например, дробь семь восьмых показывает семь восьмых части от единицы.
Обозначенное таким образом число называют рациональным числом. При этом p называется числителем дроби (он всегда находится над чертой), а q – знаменателем дроби (он всегда находится под чертой).
Рассмотрим виды обыкновенных дробей. Обыкновенные дроби можно разделить на следующие виды – правильные, когда числитель меньше знаменателя, и неправильные, когда числитель равен или больше знаменателя.
Сколько часов содержится в четверти суток?
Так как в сутках 24 часа, то нам по условию надо найти четвёртую часть, т. е. разделить двадцать четыре часа на четыре части.
Решим задачу, используя понятие обыкновенной дроби.
В коробке находилось два вида конфет: 5 шоколадных и 6 карамелек. Какую часть всех конфет занимают карамель и шоколад?
Решение: для начала найдём общее количество конфет в коробке, для этого сложим все виды конфет.
5 + 6 = 11 – конфет в коробке.
Теперь можно найти, какую часть от общего количества конфет занимает карамель, а какую шоколадные конфеты. Для этого запишем результат в виде обыкновенной дроби, где в знаменателе укажем общее число конфет. Пять одиннадцатых – часть шоколадных конфет, а шесть одиннадцатых – часть карамели.
№ 1. Сколько минут содержится в одной трети часа?
Решение: для решения этой задачи достаточно вспомнить, что 1 ч = 60 мин.
Найдём третью часть от 60 минут, для этого:
№ 2. Длина отрезка АВ равна 10 см. Чему равен отрезок, длина которого составляет две пятых от длины отрезка АВ?
Решение: сначала найдём, чему равна одна часть из 5 отрезков.
10 см : 5 = 2 см – одна часть.
По условию задачи нужно найти 2 части из пяти, поэтому: 2 см · 2 = 4 см
Прохождение программы курса математики 5–6-х классов за 1,5 учебных года
Разделы: Математика
Математическое образование в нашей стране получают все школьники, начиная с первого года обучения и до последнего. Само собой разумеется, что лишь небольшая часть обучающихся впоследствии станет сама развивать математику. Но применять математические знания и методы станут все. Очень важно, чтобы учащиеся видели прикладные возможности всех разделов математики и почувствовали значение строгих логических рассуждений для всех видов деятельности.
Как же строится школьный курс математики?
В курсе математики для V-XI кл. с учётом возрастных особенностей выделяются три ступени обучения: V-VI, VII-IX, X-XI классы.
В ходе изучения курса учащиеся развивают навыки вычислений с натуральными числами, овладевают навыками действий с обыкновенными и десятичными дробями, с положительными и отрицательными числами, знакомятся с буквенными выражениями, учатся составлять по условию текстовой задачи несложные линейные уравнения и решать их.
Следует отметить, что в V классе слишком много времени уделяется (по стандартной программе) повторению изученного в начальной школе.
Чтобы преодолеть такое положение вещей, делаются различные попытки, одной из которых является разработанная Г.Г. Левитасом переходная программа. Она рассчитана на изучение курса V-VI классов за один учебный год при пяти часах математики в неделю. Изучение этой программы предложено вести по учебникам Н.Я. Виленкина. При этом в течении каждой четверти программа строится из расчёта один пятиурочный цикл в неделю.
Нами было разработано планирование, рассчитанное на изучение математики в V кл. при четырёх часах в неделю, а в VI кл. при пяти часах в неделю. В пятом классе пятый час в неделю может быть использован учителем на свое усмотрение. В зависимости от уровня математической подготовки учащихся, им могут быть предложены задания развивающего характера или задания на ликвидацию пробелов по изучаемой теме. Программа рассчитана на изучение материала V-VI классов за 1,5 учебных года, и поэтому в VI классе со II полугодия необходимо приступать к изучению материала VII класса.
В рамках V класса изучаются следующие темы: натуральные числа (повторение изученного в начальной школе), обыкновенные и десятичные дроби.
В VI классе: отрицательные и положительные числа, пропорции и проценты, решение уравнений и координатная плоскость.
5 КЛАСС
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА ПО КУРСУ «МАТЕМАТИКА» В 5-КЛАССЕ (ПО ЧЕТВЕРТЯМ).
I четверть 9*4 ч.=З6 ч.
| № уроков | Содержание | Кол-во уроков |
| 1-12 | Действия с натуральными числами. | 12 |
| 13-16 | Свойства действий с натуральными числами. | 4 |
| 17-20 | Решение уравнений. | 4 |
| 21-30 | Решение задач (типа «во ск.», «на ск.», больше-меньше; «на», «в», на движение). | 10 |
| 31 | Подготовка к контрольной работе. | 1 |
| 32 | Контрольная работа №1 | 1 |
| 33-36 | Десятичная система исчисления, меры длины. | 4 |
II четверть 7*4 ч.=28 ч.
| № уроков | Содержание | Кол-во уроков |
| 36-39 | Что такое десятичная дробь. Сравнение десятичных дробей. | 4 |
| 40-43 | Сложение и вычитание десятичных дробей. | 4 |
| 44-46 | Решение уравнений. | 3 |
| 47 | Подготовка к контрольной работе. | 1 |
| 48 | Контрольная работа № 2. | 1 |
| 49-52 | Умножение десятичных дробей. | 4 |
| 53-56 | Деление десятичных дробей. | 4 |
| 57-59 | Решение уравнений. | 3 |
| 60 | Подготовка к контрольной работе. | 1 |
| 61 | Контрольная работа № 3. | 1 |
| 62-63 | Округление десятичных дробей. Прикидка | 2 |
III четверть 10*4 ч.=40 ч.
| № уроков | Содержание | Кол-во уроков |
| 64-66 | Обыкновенная дробь. Сравнение на луче. | 3 |
| 67-68 | Правильные и неправильные дроби. Сравнение с 1. | 2 |
| 69-72 | Признаки делимости. Разложение на простые множители. НОД. | 4 |
| 73-76 | Основное свойство. Сокращение дробей. | 4 |
| 77-80 | Сложение, вычитание и сравнение дробей с одинаковыми знаменателями. | 4 |
| 81 | Подготовка к контрольной работе. | 1 |
| 82 | Контрольная работа №4. | 1 |
| 83-86 | НОК. Приведение к общему знаменателю. | 4 |
| 87-90 | Сравнение, сложение и вычитание дробей с разными знаменателями. | 4 |
| 91-93 | Решение уравнений. | 3 |
| 94 | Подготовка к контрольной работе. | 1 |
| 95 | Контрольная работа №5. | 1 |
| 96-99 | Умножение обыкновенных дробей. | 4 |
| 100-104 | Деление обыкновенных дробей. | 4 |
IV четверть 8*4 ч.=32ч.
| № уроков | Содержание | Кол-во уроков |
| 105-107 | Решение уравнений. | 3 |
| 108 | Подготовка к контрольной работе. | 1 |
| 109 | Контрольная работа №6. | 1 |
| 110-113 | Смешанные числа. | 4 |
| 114-117 | Три задачи на дроби. | 4 |
| 118-121 | Решение текстовых задач (составление уравнений, проценты). | 4 |
| 122 | Подготовка к контрольной работе. | 1 |
| 123 | Контрольная работа №7. | 1 |
| 124-127 | Все действия обыкновенными и десятичными дробями. | 4 |
| 128-134 | Повторение. Итоговая контрольная работа. | 7 |
6 КЛАСС
Из программы 6 класса осталось пройти следующие темы: «Положительные и отрицательные числа», «Решение уравнений», «Координатная плоскость», «Пропорция».
За I четверть изучаются положительные и отрицательные числа, координатная плоскость. Первые уроки четверти посвящаются повторению пройденного в 5 классе.
II четверть начинается с изучения темы: «Решение уравнений», а затем до конца четверти учащиеся занимаются нахождением неизвестного члена пропорции и решают задачи на прямую и обратную пропорциональную зависимость.
С окончанием II четверти заканчивается изучение материала 6-го класса.
Технологическая карта урока «Обыкновенные дроби», 5 класс
Содержимое разработки
Технологическая карта урока
Волкова Галина Викторовна
Урок открытия новых знаний
Познакомить учащихся с понятием дроби; научить определять числитель и знаменатель дроби, что показывает числитель и знаменатель дроби, понимать, что такое половина, треть и четверть; научить записывать дроби
Обучающиеся научатся правильно читать, писать и объяснять значение дроби, находить числитель и знаменатель; рассуждать и делать выводы; слушать собеседника и вести диалог; работать в паре; излагать и аргументировать свою точку зрения; оценивать себя и товарищей.
Образовательные (формирование познавательных УУД):
воспитательные (формирование коммуникативных и личностных УУД):
умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, строить в паре продуктивное взаимодействие, воспитывать ответственность и аккуратность; осуществлять рефлексию своего отношения к содержанию темы.
Развивающие (формирование регулятивных УУД)
развивать умение, анализировать, сравнивать, обобщать, делать выводы, развивать внимание; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
методы формирования новых знаний и способов деятельности: объяснительно-иллюстративный и репродуктивный, проблемный и частично-поисковый, исследовательский
методы организации деятельности учащихся: учитель-ученик, ученик-ученик, самостоятельная работа
методы контроля и самоконтроля
методы формирования личностных результатов, ценностных ориентаций, формирования опыта положительного социального поведения
методы стимулирования и мотивации деятельности поведения
Формы работы обучающихся
Фронтальная, парная, индивидуальная, в большом классе-групповая.
Организация деятельности обучающихся на уроке:
самостоятельно определяют тему, цель урока;
выполняют самостоятельную работу с самопроверкой;
ведут диалог, отвечают на вопросы;
оценивают себя и друг друга;
Необходимое учебное оборудование
1. Организационный этап
Создать благоприятный настрой на работу
Приветствие, проверка готовности к уроку, организация внимания детей.
Включаются в деловой ритм урока.
Коммуникативные: планируют учебное сотрудничество с учителем и сверстниками.
Регулятивные: организация своей учебной деятельности
Личностные: мотивация учения
2. Постановка цели и задач урока.
Обеспечение мотивации учения детьми, принятие ими темы и целей урока.
Мотивирует учащихся, акцентирует внимание учащихся на значимость темы.
Записывают дату в тетрадь, определяют тему и цель урока.
Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме.
Коммуникативные:умение вступать в диалог, участвовать в коллективном обсуждении вопроса.
3. Актуализация знаний
Актуализация опорных знаний и способов действий.
Проверка опорных знаний
Участвуют в работе по проверке опорных знаний (индивидуально и фронтально),
Познавательные: структурирование собственных знаний.
Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками.
Регулятивные: контроль иоценка процесса и результатов деятельности.
Личностные: оценивание усваиваемого материала.
4. Изучение нового материала.
Введение понятия обыкновенная дробь, числитель, знаменатель дроби, черта дроби
Организует проблему и направляет её разрешение. Организует с помощью презентации и работы по учебнику введение новых понятий: обыкновенная дробь, числитель, знаменатель, что они означают. Акцентирует внимание на записи и чтении обыкновенных дробей.
Учитель дает возможность обучающимся самостоятельно раскрыть исторический аспект появления дробей.
В процессе разрешения проблемы обучающиеся вместе с учителем с использованием учебника вводят понятие «обыкновенная дробь»; с использованием демонстрационного материала знакомятся с понятиями числитель, знаменатель, черта дроби, читают готовые записи дробей, определяют место нахождения числителя и знаменателя, их значения.
Познавательные: решение проблемы, построение логической цепи рассуждений;
Личностные: формировать способность к эмоциональному восприятию математических рассуждении.
Регулятивные: определение последовательности промежуточных целей с учётом конечного результата;
Коммуникативные:постановка вопросов, инициативное сотрудничество.
5.Этап первичного осмысления и закрепления знаний.
Мотивировать учащихся к деятельности; контролировать выполнение заданий
Организует решение задач выявляет уровень усвоения знаний, а также устанавливает причины выявленных ошибок.
Работают в парах, индивидуально
и фронтально над поставленными задачами. Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения задач
Познавательные: формирование интереса к данной теме;
построение логической цепи рассуждений;
формирование позитивной самооценки
Коммуникативные: уметь оформлять свои мысли в устной и письменной форме; слушать и понимать речь других.
Регулятивные: умение анализировать правильность выполнения действий и вносить необходимые коррективы
Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.
Учащиеся сменили вид деятельности и готовы продолжить работу.
7. Применение знаний и умений в новой ситуации.
Организует решение задач в изменённой ситуации, выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок.
Работают в парах, индивидуально
и фронтально над поставленными задачами. Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения задач.
Познавательные: формирование интереса к данной теме;
решение проблемы, построение логической цепи рассуждений;
Личностные: формирование готовности к самообразованию,
формирование позитивной самооценки
Коммуникативные: уметь оформлять свои мысли в устной форме; слушать и понимать речь других.
Регулятивные: умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы.
8. Рефлексия (подведение итогов урока)
Дать количественную оценку работы учащихся
Подводит итоги работы
Учащиеся сдают карточки урока.
Регулятивные: оценивание собственной деятельности на уроке
9. Информация о домашнем задании
Обеспечение понимания детьми содержания и способов выполнения домашнего задания
Дает комментарий к домашнему заданию
Учащиеся записывают в дневники задание.
Личностные: формирование готовности к самообразованию,
формирование объективной самооценки
1. Организационный этап
Цель: создать благоприятный психологический настрой на работу, мотивировать учащихся к учебной деятельности; осознанное вхождение учащегося в пространство учебной деятельности.
Учитель приветствует учащихся, проверяет их готовность к уроку.
жёлтый – сомневаюсь, справился с задачей, но возникали сложности,
красный – к дальнейшему движению не готов, с задачей не справился
Учащиеся слушают учителя, проверяют готовность рабочего места, знакомятся с картой урока.
2. Постановка цели и задач урока.
Цель: Обеспечение мотивации учения детьми, принятие ими целей урока.
На экран выводятся цели урока, продублированные в карте урока:
ЦЕЛИ, С КОТОРЫМИ Я СЕГОДНЯ ПРИШЕЛ НА УРОК:
1. Получить новые знания.
2. Получить пятерку.
3. Научиться грамотно, говорить, выражать свои мысли.
4. Пообщаться с одноклассниками.
5.Провести интересно время.
6. Показать себя, свою эрудицию.
7. Получить то, что пригодиться в жизни
8. Просидеть спокойно 45 минут.
Поставьте знак «+» против целей, которые подходят вам. Можете дополнить список.
Учащиеся определяют личностные цели урока.
3. Актуализация знаний
Цель: актуализация опорных знаний и способов действий.
1.Проверим теоретический материал в форме игры «да-нет» (да – хлопок). Вопросы выведены на экран и читаются учителем :
-натуральные числа применяют для счёта натуральных предметов
— натуральные числа появились 30 лет назад,
— натуральные числа появились ещё до нашей эры
— 0- натуральное число,
— кроме натуральных существуют другие числа
— натуральные числа можно складывать, вычитать, умножать, делить
— сумма натуральных чисел есть натуральное число. Приведите пример.
Проверка: после каждого ответа (хлопка) учитель вслух произносит правильный ответ.
— Значит, кроме натуральных, существуют другие числа. С ними и познакомимся сегодня.
2.- Перед вами задания для устного счёта. Вместо привычных знаков действий – знаки, используемые в старину. Определите смысл каждого знака и запишите в карту.
Проверьте (слайд). Выполните вычисления. Результаты запишите в тетрадь.
— Проверьте вычисления (слайд)
-Какое задание показалось самым трудным? Почему?
— Знания, полученные сегодня на уроке, помогут вам.
Повторяют теоретический материал в ходе игры. Приводят примеры в доказательство ответов на два последних вопроса.
Самоконтроль и самооценка.
Определяют смысл математических знаков и записывают в карту.
Выполняют устные вычисления, результаты вычислений записывают в тетрадь.
Приходят к выводу в недостаточности знаний, чтобы выполнить задание.
4. Этап изучение нового материала.
Цель: введение понятия обыкновенная дробь, числитель, знаменатель дроби, черта дроби на имеющихся знаниях из начальной школы
Начнём нашу работу с отрывка из стихотворения Людмилы Зубковой:
Мы делили апельсин,
Много нас, а он один.
Эта долька – для ежа,
Эта долька – для стрижа,
Эта долька – для утят,
Эта долька – для котят,
Эта долька – для бобра,
— Какой фрукт делили звери? (апельсин)
— На какие по размеру части делили апельсин? (равные)
— На сколько равных частей надо разделить апельсин, чтобы все звери получили поровну? (на пять)
— Какую часть получит каждый? (одну пятую)
— Как бы вы это записали?
— Какой из предложенных вариантов наиболее удобный?
— Как вы думаете, какой способ используют в современной математике?
— О правильности вашего предположения узнаем немного позднее.
— А в жизни бывают ситуации, когда целое нужно разделить на части? Приведите примеры.
Выполним это на практике.
— Сколько в классе человек? (6)
— Разделите яблоко на равные части и угостите каждого.
— Какую часть яблока получил каждый из нас? (одну шестую)
— Как мы это можем записать?
— Проблема деления целого на части и записи результата возникла ещё в далёкой древности. Об этом нам расскажет …
— Сейчас запись изменилась. И результат деления называется не «ломаным числом». Об этом вы узнаете из учебника. Прочитайте текст на стр. 170 и ответьте на вопросы:
— Как «ломаные» числа называются сейчас?
— Когда возникают дробные числа?
— Как записываю дробные числа сейчас? Приведите пример.
— Как вы думаете, почему данные числа называют дробными? (дробить, т. е. делить).
— У нас есть поговорка: “попал в тупик”, т.е. попал в такое положение, откуда нет выхода. У немцев аналогичная поговорка гласит: “попасть в дроби”. Она означает, что человек, попавший в “дроби”, оказался в затруднительном положении. Ребята, как вы думаете, а смогут ли нас дроби поставить в затруднительное положение? Проверим.
— Математика уважительно относится к своим объектам (подопечным)
Каждый элемент в записи дроби имеет своё имя (название). Об этом узнаем в ходе просмотра демонстрационного материала.
— Давайте подумаем, что показывыает знаменатель, а что числитель (в случае необходимости возвращаемся к демонстрации)
— Итак, мы сегодня познакомились с новой группой чисел. Как они называются. Запишем в тетрадь тему урока.(Обыкновенные дроби)