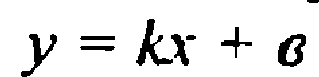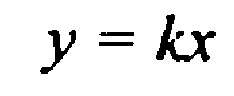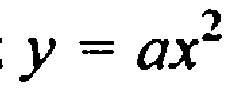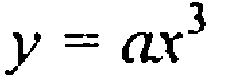в каком классе проходят графики функций
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №48. Функции. Свойства функций и их графики. Исследование функций.
Перечень вопросов, рассматриваемых в теме:
Глоссарий по теме урока
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
х – независимая переменная, аргумент,
Множество значений аргумента функции называется областью определения функции и обозначается D(y).
Множество значений, которые принимает сама функция, называется множеством значений функции и обозначается Е(у).
Функция у = f(х) называется четной, если она обладает двумя свойствами:
Функция у = f(х) называется нечетной, если она обладает двумя свойствами:
для любого х из области определения выполняется равенство f(-х)=-f(х).
Значения аргумента, при которых значение функции равно 0, называются корнями (нулями) функции.
Функция у=f(x) возрастает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких, что х1 у2.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2015. С. 98-118, 271-307.
Шахмейстер А.Х. Построение и преобразование графиков. Параметры. Ч.2-3. СПб.: Петроглиф; М.: МЦНМО, 2016. 392 с. С.73-307.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”.
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
1. Исследование функции и построение графика
Схема исследования функции на примере функции
1) Область определения функции
Знаменатель дроби не равен нулю:
Получили область определения
D(y)=
Отыскание Е(у) можно свести к решению уравнения с параметром у. Все значения параметра у, при которых уравнение имеет хотя бы одно решение, и составят Е (у).
Получили
D(y)= 

следовательно, функция четная и ее график симметричен относительно оси ОУ
Для нахождения нулей функции необходимо решить уравнение
Уравнение не имеет действительных корней, значит, нулей у данной функции нет, ее график не пересекает ось ОХ
у>0 при
у 2 у.е. Если на втором объекте работает t человек, то их суточная зарплата составляет t 2 у.е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у.е. в этом случае придется заплатить рабочим?
1 этап. Ведем переменную, выразим нужные компоненты, составим искомую функцию.
Пусть на 1 объект направлено х рабочих, суточная зарплата которых составит 4x 2 у.е.
Причем 0≤ x ≤ 24, x ϵ N.
3 этап. Перевод на язык задачи
Поскольку x ϵ N, подходящим будет ближайшее к вершине натуральное значение, x=5 (рабочих) – на 1 объекте.
24-5=19 (рабочих) – на 2 объекте.
Наименьшее значение f(5)=125+240-576=461 (у.е.) – наименьшая суточная выплата.
Примечание: исследовать функцию также можно было с помощью производной.
Ответ: 5 рабочих на 1 объекте, 19 – на втором, 461 у.е. – наименьшая суточная выплата.
Примеры и разбор решения заданий тренировочного модуля
1. Исследуйте функции на четность.
область определения – множество действительных чисел – симметрична относительно нуля
Данная функция одновременно четна и нечетна.
область определения – множество действительных чисел – симметрична относительно нуля
преобразуем функцию, применив формулы приведения: sin(x+5π/2)=cos x
у= cos x – четная функция, значит, исходная функция также четная
логарифмируемое выражение должно быть положительным
Найдем область определения D(f)
Проверим второе условие
Полученное в результате подстановки –х в функцию выражение, очевидно, не равно f(x), не дает пока понимания о выполнении условия нечетности.
домножим на сопряженное
Теперь можем сделать вывод: f(-x)=-f(x), функция нечётная.
и четная, и нечетная
2.
Используем функциональный подход при решении данной задачи. Представим каждое из уравнений как функции. Построим их графики. Единственное решение системы будем интерпретировать как единственную точку пересечения графиков функций первого и второго уравнений.
Второе уравнение проще, но содержит параметр. Перепишем его в явном виде для функции, выразив у: у=-х+а.
В таком виде понятно, что данное уравнение задает множество прямых, параллельных у=-х.
Основные виды функций, изучаемых в курсе «Алгебра» за 7кл
Содержимое разработки
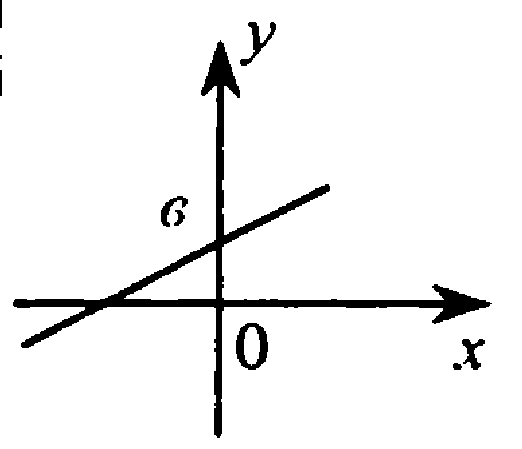
Прямая не проходящая через начало координат, достаточно 2 точек.
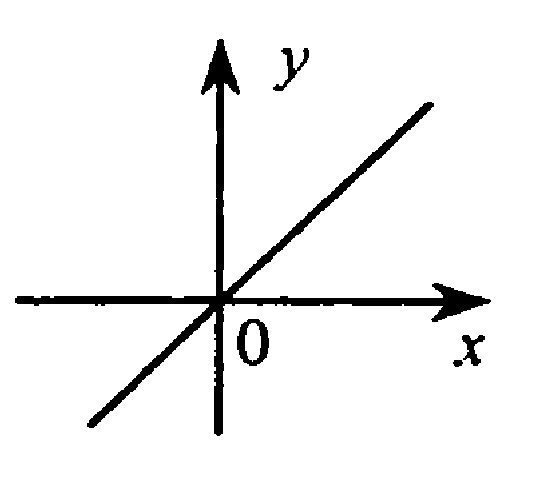
Прямая проходящая через начало координат, достаточно 2 точек.
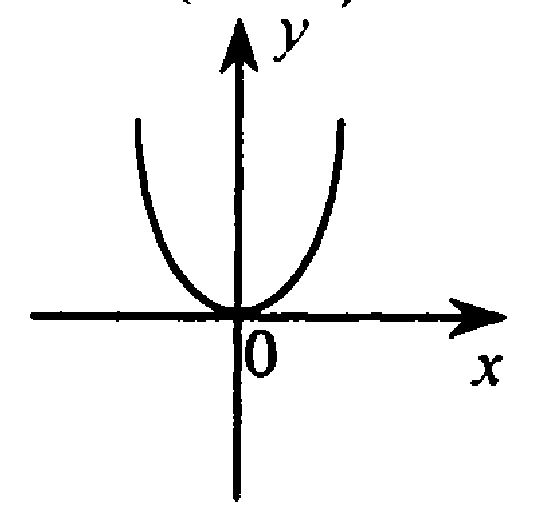
Парабола, достаточно 5 точек, две полож нуль и две отриц.
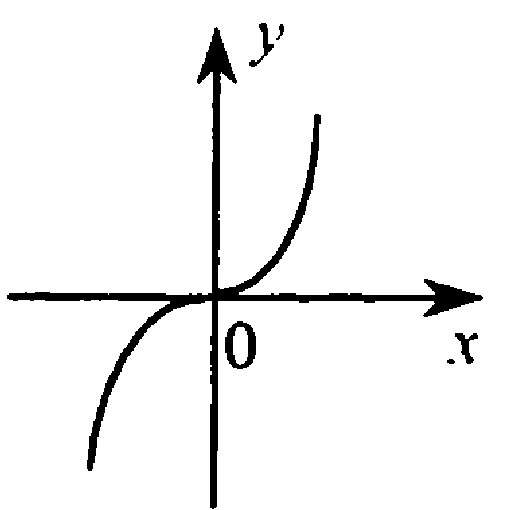
достаточно 5 точек, две положительные нуль и две отриц.
Точка О(0;0) не принадлежит графику
Точка О(0;0) принадлежит графику
Точка О(0;0) принадлежит графику
Точка О(0;0) принадлежит графику
k 0, из 1 в 3 четверть
а0, из 1 в 3 четверть
Относительно оси y.
Относительно начала координат.
Часто задаваемые вопросы
— Условие пересечения графиков двух линейных функций?
-Условие параллельности графиков двух линейных функций?
Проверьте принадлежит ли точка графику функции у=5х+3?
Не принадлежит, если верно, то принадлежит.
Как найти координаты точек пересечения функции с осями? Если с осью Х –то нулим «у», если с осью Y, то нулим «х».
Как найти точки пересечения графиков функций? Графически или аналитически (прировнять правые чести и решить уравнение, найти вторую координату)
Графики функции. 9-й класс
Разделы: Математика
Класс: 9
Цель урока – повторить и систематизировать знания об изученных функциях и их графиках.
Для достижения цели поставлены три задачи:
– обучающая: повторить свойства изученных функций, а также их графики.
– развивающая: развивать математическую речь, логическое мышление, познавательный интерес к предмету, воображение, память;
– воспитательная: воспитывать аккуратность, внимание к слову учителя.
Деятельность уч-ся
Письмена, устная работа
Тип урока: обобщения и систематизации знаний.
Оборудование и оформление: проектор, таблица, сигнальные карточки, шаблоны функций у = х?, у = х?
Ход урока
1. Оргмомент.
Объявление темы и цели урока. Запись в тетради даты, темы.
2. Математический диктант.
Диктант проводится с целью выявления пробелов в знаниях учащихся, для того, чтобы в дальнейшем их можно было ликвидировать. Учащиеся получают два чистых листа бумаги и копирку и выполняют работу под копирку в двух экземплярах.
1 вар: х 2 – х-6 >0 2 вар: х 2 – х – 6 2 , у = х 2 , у = (х+3) 2 -2,
у = х 2 -2. Построение графиков производится с использованием шаблонов графиков функций.
При построении графиков функций ученики рассказывают свойства этих функций.
Выполните задания: график какой функции изображён на рисунке? (Слайд 5)
В) Построение графика функции y = ах 2 + вх + с
Выполните задание: квадратичная функция y = ax 2 + bx + c задана графиком, изображённым на рисунке. Определите знаки коэффициентов a, b и c. (Слайд 6)
Чтобы построить график функции y=|f(x)|, достаточно построить график функции y=f(x) и ту часть графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси 0x. (Слайд 8)
5. Самостоятельная работа.
Задания самостоятельной работы дифференцированы по сложности. (Слайд 9)
6. Подведение итогов.
Рефлексия.
Включаем светофор: если на уроке ученику было всё понятно и не возникли вопросы, то он поднимает сигнальную линейку зелёного цвета, в противном случае – красную.
7. Домашнее задание. (Слайды 10, 11)
1. Повторить свойства функции у = 
3. Построить график функции вида y=f(x).
4. Объясните построение графика функции 
Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Парабола
Гипербола
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
0″ height=»346″ width=»346″ sizes=»(max-width: 346px) 100vw, 346px» data-srcset=»/wp-content/uploads/2017/01/Гипербола-1.png 346w,/wp-content/uploads/2017/01/Гипербола-1-150×150.png 150w,/wp-content/uploads/2017/01/Гипербола-1-300×300.png 300w,/wp-content/uploads/2017/01/Гипербола-1-176×176.png 176w,/wp-content/uploads/2017/01/Гипербола-1-60×60.png 60w, https://epmat.ru/wp-content/uploads/2017/01/Гипербола-1.png»>
Если k 0, ветви гиперболы проходят через II и IV четверти.
Квадратный корень
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Построение графиков функций
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные онлайн занятия по математике для учеников с 1 по 11 классы! Приходи на пробное занятие с нашими лучшими преподавателями!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)