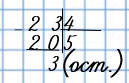в каком классе проходят деление с остатком

Деление с остатком

Начнём рассмотрение новой темы с решения задачи.

Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?

Каждый ребёнок получил по 4 конфеты.

На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?

Каждый получил по 2 конфеты и 2 конфеты остались лишними.

Как сделать проверку?

Правило 1

Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.

Правило 2

При делении с остатком остаток всегда должен быть меньше делителя.

Порядок решения

1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.

2. Вычитаю из делимого найденное число: 14 − 10 = 4

3. Сравниваю остаток с делителем

Проверка деления с остатком

1. Умножаю неполное частное на делитель.

2. Прибавляю остаток к полученному результату.

3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.

Деление в столбик

В 23 содержится 5 раз по 4, и ещё остаётся 3.

Решение записывают так:

23 : 4 = 5 (ост. 3) или так:

Поделись с друзьями в социальных сетях:

Источник

Конспект урока по математике УМК «Школа России» 3 класс «Деление с остатком»

Ищем педагогов в команду «Инфоурок»

3 класс УМК «Школа России»

ТЕМА УРОКА: Деление с остатком

Цели: обучить алгоритму выполнения деления числа с остатком, закреплять вычислительные навыки, умение решать задачи изученных видов.

Познакомить учащихся с алгоритмом деления числа с остатком;

С помощью практических упражнений научить обучающихся производить

деление с остатком;

Совершенствовать вычислительные навыки, умение решать задачи.

Развивать познавательную активность, интерес к предмету; умение рассуждать и

Развивать логическое мышление, внимание, память, пространственное воображение.

Воспитывать коммуникативные качества,

Наблюдательность и любознательность,

Развивать познавательную активность, формировать навыки работы в парах и группах.

Формируемые в рамках урока универсальные учебные действия:

Коммуникативные: развивать навыки учебного сотрудничества, умение работать в паре, в группе, умение оформлять свои мысли в устной форме, учить понимать возможности различных позиций и точек зрения;

Познавательные: ориентироваться в материале учебника, умение работать с информацией, умение составлять вопросы по пройденному материалу, выстраивать цепочку логических рассуждений, делать выводы и фиксировать их с помощью математических записей, умение находить границу области «знания» и «незнания», видеть область применения полученных знаний при решении практических задач.

Личностные: понимание значения математических знаний в собственной жизни и деятельности людей, укрепление интереса к изучению математики, формирование понимания основных моральных норм: взаимопомощи, ответственности; учебной мотивации.

ТИП УРОКА: Изучение нового материала и первичное закрепление.

Оборудование: Математика: 3 класс, 2 часть, М.И. Моро. Школа России. «Просвещение» 2016г.

IV. Первичное усвоение новых знаний.

V. Закрепление изученного материала .

Давайте, ребята, учиться считать,
Делить, умножать, прибавлять, вычитать,
Запомните все, что без точного счёта,
Не сдвинется с места любая работа.

Посмотрите, друг другу в глаза, улыбнитесь, пожелайте друг другу удачи, хорошего настроения. (Минутка создания настроения).

Я желаю вам уже сегодня на уроке показать свои знания. Удачи! В добрый путь за знаниями!

Сегодня урок необычный, мы отправимся в небольшое путешествие по станциям.

Но любая в математике работа,
Не обходится без устного счёта.

Итак, первая станция – «Разминка».

-Игра «Молчанка» (сигнальные карточки)

(проверка таблицы умножения)

2. Веселые задачи (устно).

— На майках 15 спортсменов нашиты их порядковые номера. Каких номеров больше: четных или нечетных? (Нечетных.)

— Имеется кусок веревки длиной 8 м. Как, не пользуясь метром, отрезать 6 м? (Разделить пополам и получившуюся половинку — еще пополам.)

— Летела стая тетеревов, села в роще на деревья. По двое сядут — одно дерево лишнее. По одному сядут — один тетерев лишний. Сколько деревьев и тетеревов? (4 тетерева, 3 дерева.)

3. Найдите лишнее выражение: (работа в парах)

Как вы думаете, можем мы решить эту проблему?

На пути у нас остановка! Это не конец путешествия, а начало решения проблемы!

3. Открытие новых знаний.

Мы отправляемся на станцию «Проблемкино». Пока мы едем, попробуем решить такую задачу.

— На тарелке лежало 10 пирожков. Как разделить пирожки 3 детям поровну?

Работа над задачей.

— Сколько было пирожков? (10 пирожков было)

— Сколько было детей? (3 ребёнка)

— Что нужно сделать по условию задачи? (пирожки нужно разделить поровну, 10 разделить на 3)

( К доске вызвать 3 человека )

— Разделите пирожки поровну.

— Сколько пирожков досталось каждому ребёнку? ( Каждому ребёнку досталось по 3 пирожка)

— Сколько пирожков осталось на тарелке? (на тарелке остался 1 пирожок)

В математике принято количество оставшихся предметов записывать так:

-Сколько разделили без остатка? (9) Почему? (делится по таблице умножения)

-Что важно знать при делении? (таблицу ×)

-Так сколько раз по 3 содержится в 10? (3 ост. 1)

— Запишите решение этой задачи к себе в тетрадь.

10 : 3 = 3 (ост. 1) Попробуйте прочитать это выражение, используя названия компонентов.

Сравните остаток и делитель? (остаток меньше делителя)

Какой можно сделать вывод? (Мы разделили число 10 на 3, у нас получилось 3, осталось 1.)

Кто знает, как называется действие, которое мы сейчас выполнили? (Деление с остатком.)

Назовите делимое. (10.)

Назовите делитель. (3.)

Назовите частное. (3.)

Что такое 1? (Остаток.)

При делении с остатком результат записывают двумя числами. Первое число называют частным, второе – остатком.

Сформулируйте тему и задачи урока.

Тема урока – деление чисел с остатком.

Давайте решим с объяснением сейчас выражение: 18 : 4 (объясняет ученик)

IV. Первичное усвоение новых знаний.

-Прочитайте на с. 26, как разделить 17 на 3.

— Как называются компоненты действия в таких примерах?

-Прочитайте равенство на математическом языке.

-Правильные ли выводы вы сделали?

— Устное выполнение. № 1 (с. 26).

Решение упражнений на формирование навыка выполнения действия деления.

Итак, мы на станции «Проблемкино». Будем закреплять новые знания.

— Рассмотрите первый пример.

— Какое самое большое число до 7 делится на 3 без остатка? (6)

— Сколько получится, если 6 разделить на 3? (2)

— Сколько останется? (1)

На доске примеры, решите с объяснением.

Какое правило при делении с остатком мы должны всегда помнить?

При делении остаток всегда должен быть меньше делителя.. (хором)

Но прежде, чем приступим к таким ответственным действиям, позволим себе отдохнуть.

V. Закрепление изученного материала .

Сейчас отправляемся на станцию «Проверялкино».

— Как удобнее оформить краткую запись? (С помощью таблицы.)

— Что обозначают числа 54, 90, 72? (Общее число листов.)

— Что обозначает число 3? (Количество тетрадей.)

— Что надо узнать в задаче? (Сколько таких тетрадей получится из 90 листов, из 72 листов.)

— Что сказано о количестве листов в 1 тетради? (Одинаковое.)

— А теперь поработайте в парах, подумайте, как решается задача, и решите её самостоятельно по вариантам.

Проверка: 2 ученика работают за доской, затем объясняют решение задачи.

1). 54:3=18(л.)- в одной тетради.

Ответ: 5 тетрадей получится из 90 листов бумаги.

1). 54:3=18(л.)- в одной тетради.

Ответ: 4 тетради получится из 72 листов.

2 . Выполнение заданий в рабочей тетради

( Работа в парах. Проверка )

( Самостоятельное выполнение. Взаимопроверка.)

Вот мы и прибыли на станцию « Итоговая ».

VI Подведение итогов, рефлексия.

С каким вычислительным приемом вы познакомились сегодня на уроке? (Решали примеры и задачи на деление с остатком)

Верно ли мое утверждение 🙁 сигнальные карточки)

— Все примеры на деление имеют остаток.

— Некоторые примеры на деление имеют остаток.

— Иногда остаток меньше делителя.

— Всегда остаток меньше делителя.

— Каждый остаток находим вычитанием.

— Кто хорошо понял тему и может объяснить ее товарищам?

— Какие задания на уроке вам больше всего понравилось выполнять?

Подведём сейчас итог,

Что пошло ребятам впрок.

Каждый пальчик разомнем.

Поднимите, пожалуйста, одну руку (показываю)

Оценка урока по «Методу пяти пальцев».

М (мизинец) – Какое математическое открытие я сделал на уроке? (остаток меньше делителя)

Б (безымянный) – Чему я научился? (выполнять деление с остатком)

С (средний) – Пригодятся ли мне эти знания в жизни? Где?

У (указательный) – Кому я сегодня помог?

Б (большой) – Какое у меня настроение? (У меня такое – показываю большой палец )

Показываю свою руку с раскрытыми пальцами и говорю:

— Вот сколько добрых дел мы сегодня сделали!

-Понравился ли вам урок? Почему?

Молодцы! Вы сегодня очень хорошо поработали. Спасиб о за урок.

Источник

Что такое деление с остатком: примеры для ребенка в 3, 4 классе

Как научить ребенка делению? Самый простой метод – выучить деление столбиком. Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически….

Как проводится

Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.

Приведем простой пример того, как делить с остатком:

Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:

5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.

Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.

Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.

Основные этапы:

Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя.

Когда делитель больше делимого

Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача: необходимо не разделить, а найти остаток! Дробная часть им не является! Как решить такую задачу?

Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.

Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6 больше 5.

По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.

Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны освоить таблицу умножения, что позволяет им совершать деление двузначных чисел на однозначные.

Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?

Примеры:

Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.

Остаток: 3*4=12, 14-12=2.

Ответ: неполное частное 4, осталось 2.

Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу.

Еще одна задача: 3 пирожка надо разделить на двоих.

4 пирожка разделить на двоих.

5 пирожков разделить на двоих.

Это интересно! Изучение точного предмета: натуральные числа — это какие числа, примеры и свойства

Работа с многозначными числами

Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.

Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.

Разделим многозначные числа на двузначные: 386:25

Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее. Рассмотрим подробнее:

386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.

Первый уровень

Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?

25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.

Ответ – 1. Записываем единицу в зону не полного частного.

38-25=13. Записываем число 13 под чертой.

Второй уровень

13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?

25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.

Вычисляем остаток:

136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.

Ответ: неполное частное равно 15, в остатке 11.

А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.

Приведем примеры на деление с трех- и четырехзначными числами:

75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно. Проводим вычисления.

75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.

Находим остаток: 386-375=11. 11 больше 75? Нет. Еще остались цифры у делимого? Нет. Вычисления закончены.

Ответ: неполное частное = 5, в остатке 11.

Выполняем проверку: 11 больше 35? Нет – деление провести нельзя. Подставляем третье число – 119 больше 35? Да – действие провести можем.

35*1=35, 35*2=70, 35*3=105, 35*4=140. 140 больше 119 – возвращаемся на один шаг назад. Записываем 3 в зону неполного остатка.

Находим остаток: 119-105=14. 14 больше 35? Нет. Остались цифры у делимого? Нет. Вычисления закончены.

Ответ: неполное частное = 3, осталось 14.

Проверяем: 11 больше 99? Нет – подставляем еще одну цифру. 119 больше 99? Да – начинаем вычисления.

99*1=99, 99*2=198 – перебор. Записываем 1 в неполное частное.

Находим остаток: 119-99=20. 20&lt,99. Опускаем 5. 205&gt,99. Вычисляем.

99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.

Находим остаток: 205-198=7.

Ответ: неполное частное = 12, остаток 7.

Деление с остатком примеры

Учимся делить в столбик с остатком

Вывод

Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно.

Это интересно! Легкие правила округления чисел после запятой

Источник

Математика. 3 класс

Конспект урока

Математика, 3 класс

Урок № 46. Деление с остатком

Перечень вопросов, рассматриваемых в теме:

1. Может ли при делении число не разделиться полностью?

2. В каких случаях выполняется деление с остатком?

3. Какое правило поможет научиться делить с остатком?

Деление – это обратное действие умножению.

Делимое – компонент деления, число которое делят.

Делитель – компонент деления, число на которое делят.

Частное – результат деления.

Неполное частное – результат деления с остатком.

Обязательная литература и дополнительная литература:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для

общеобразовательных организаций М.; Просвещение, 2017. – с. 26.

2. Математика. 3 класс. Часть 2. / Л. Г. Петерсон – М.: Ювента, 2013 – с. 96.

Теоретический материал для самостоятельного изучения

Как узнать, сколько раз по три содержится в семнадцати? Разделим семнадцать на три. В семнадцати пять раз содержится по три и ещё останется два.

Два – это остаток. Число не разделилось полностью, поэтому частное называют неполное.

При делении с остатком можно пользоваться рисунком.

Рисунок может быть не всегда удобным. Записывать деление с остатком можно в столбик или как ещё называют уголком.

Рассмотрим пример. Семнадцать надо разделить на три.

При записи уголком неполное делимое пятнадцать пишем под числом семнадцать, а неполное частное под делителем. Это число пять. Из семнадцати вычитаем пятнадцать останется два. Это остаток.

При делении с остатком результат записывают двумя числами: неполное частное и остаток.

Выполним тренировочные задания.

№ 1. Вставьте пропущенные числа:

Ответ: 59 : 8 = 7 (ост.3)

№ 2. Соотнесите деление и результат.

Ответ: 24 : 5 = 4 (ост. 4)

«Троим детям раздали 7 пирожных. Сколько получилось у каждого и сколько осталось?».

№ 4. Выделите цветом, какой остаток может быть при делении на 4:

Источник

Урок математики во 2-м классе «Деление с остатком»

I. Психологический настрой детей на урок.

— Здравствуйте, ребята! Садитесь.

-Вот мы и пожелали друг другу здоровье.

-А какое сегодня у вас настроение? А почему? И у меня сегодня тоже хорошее настроение, потому что у меня появились новые друзья. Это вы.

Я рада видеть каждого из вас.
И пусть прохлада в окна дышит,
Нам будет здесь уютно, ведь ваш класс
Друг друга любит, чувствует и слышит.

-Сейчас я проверю, как вы умеете внимательно слушать и слышать.

(ТИХО)Открыли тетради, записали число, классная работа.

-Начнём урок с математического диктанта. Записываем в тетрадь ответы в строчку. Проговариваю 2 раза:

-Давайте проверим, какие ответы у вас получились? Вот правильные ответы. Сравните и исправьте ошибки, я надеюсь, что их не много.

-Каким арифметическим действием вы пользовались, выполняя диктант? (Делением)

-Сегодня мы познакомимся с новым видом деления, будьте внимательны. А кто нам в этом поможет, мы узнаем, расположив ответы в порядке возрастания? Запишите в тетрадь и расшифруйте слово.

-Давайте представим, что на улице весна. Страшила решил посадить огород. Но у него здесь такой беспорядок. (ПОКАЗАТЬ)

III. Практическая работа.

-Давайте посадим овощи красиво на грядки. Возьмём план огорода и приступим к делу.

(У каждого ребёнка на столе план огорода, 13 морковок, 14 свёкл)

-Итак задача 1. Посчитайте сколько морковок посадил Страшила? (13)

-Пересадим эти морковки поровну на две длинные грядки. Морковку аккуратно снимаем и сажаем на грядки.

-Давайте запишем наше действие в виде выражения. Какое арифметическое действие используем для записи? Сколько всего морковок? На сколько сажали грядок? Сколько на каждой грядке? Все морковки посадили? Запишем этот остаток в скобках.

-Молодцы, вот мы и справились с 1 задачей.

-А теперь послушайте загадку:

Хотя я сахарной зовусь,
Но от дождя я не размокла,
На борщ всегда я пригожусь.
Крупна, кругла,
Сладка на вкус
Узнали вы? Я …
(свёкла)

-Задача вторая. Сколько свёкл посадил Страшила? (14)

-Пересадим свёклу поровну на 3 свободные грядки. Приступайте к работе.

-Запишем в тетради наше действие в виде выражения? Кто запишет на доске?

-Ребята, у всех так получилось? Молодцы. Со 2 задачей тоже справились.

IV. Сообщение темы урока.

— Посмотрите внимательно на наши выражения. Что необычного в этом делении? Оказывается, не все числа делятся нацело. Есть ещё деление, которое называется «Деление с остатком». Это и есть тема нашего урока. Как и в обычном делении, каждый компонент в выражении имеет своё название. Давайте вспомним.

V. Знакомство с новым материалом.

— Страшила тоже посадил свёклу поровну на каждую грядку. Посмотрите, как он справился с этой задачей.

-А кто из нас лучше справился? Почему вы так думаете? Что можно сделать с этим остатком?

-Как же нам не допустить ошибки при делении с остатком. В чём здесь секрет? Сравните остаток и делитель? Как делил Страшила мы никогда делить не будем.(ЗАЧЁРКИВАЕМ). А согласен ли с нами автор нашего учебника откройте с. 92 и прочитайте правило.

-Какие остатки могут получаться при делении на 4, на7? Как проверить правильно мы выполнили деление с остатком?

13 : 2 = 6 (ост. 1)
2· 6+1=13

14 : 3 = 4 (ост. 2)
3· 4+2=14

VII. Закрепление пройденного материала.

-Теперь я вам открою ещё один секрет, как быстро выполнить деление с остатком. Например

-17-не делится нацело на 3 перейдём к меньшему числу 16 делится на 3,спускаемся дальше 15 делится на 3 получится 5. А как найти остаток?

-Давайте теперь вы попробуете

— Назовите самое большее число до 23, которое делится на 4. Сейчас Страшила проверит, как вы сами выполняете деление с остатком.

(ЛОТО) В тетради решите эти примеры.

(На доске готовые ответы при переворачивание получается дровосек)

Найдите верный ответ и прикрепите к нужному примеру.

(ДРОВОСЕК) А этот герой сказки Волкова вам знаком?

-Чтобы на огороде всё выросло его надо поливать. Давайте решим задачу. Прочитайте её.

— Изобразим условие задачи в виде схемы. Что нам известно? Целое мы изобразим отрезком. Значит, отрезок это…80 литров. Что ещё известно? Прочитаем вопрос задачи. Что найдём первым действием? Какие будут следующие ваши действия? Кто хочет решить эту задачу у доски? …. ты решаешь задачу с комментированием, а все остальные записывают решение задачи.

Ответ: 10 литров в каждом маленьком ведре.

Теперь наш огород не засохнет. ( ВРЕМЯ)

-Страшила с другом решил собрать урожай. Все овощи, а их у нас сколько (27) он разложил в 5 корзин поровну. Сколько овощей в каждой корзине? Запишем наше действие вы в тетрадях, а …. на доске.

-Что нового вы сегодня узнали на уроке?

О чём нельзя забывать при делении с остатком?

Страшила и его друзья, чтобы проверить, как вы научились выполнять деление с остатком. Пример Тотошки, а теперь Элли. Дровосек наверно подготовил самый сложный пример. Лев тоже придумал пример. А вот и Страшила. Страшиле мы помогли, и он благодарит нас за дружную работу.

Придумать и нарисовать математическую семью, в которой есть делимое, делитель, частное и, конечно, Остаточек, а кому будет сложно, тот составит 5 примеров на деление с остатком и решит их.

-Вам было интересно на уроке? Мне тоже было приятно с вами работать. Вы помогали и поддерживали друг друга, как настоящие друзья. Спасибо вам за урок. Страшила и его друзья расстаются с вами весёлой песенкой.

Источник