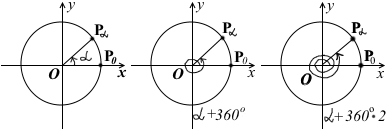в каком классе начинается тригонометрия в школе
Тригонометрия
Когда-то в школе на изучение тригонометрии выделялся отдельный курс. В аттестат выставляли оценки по трём математическим дисциплинам: алгебре, геометрии и тригонометрии.
Затем в рамках реформы школьного образования тригонометрия перестала существовать как отдельный предмет. В современной школе первое знакомство с тригонометрией происходит в курсе геометрии 8 класса. Более глубокое изучение предмета продолжается в курсе алгебры 10 класса.
Определения синуса, косинуса, тангенса и котангенса сначала даются в геометрии через связь сторон прямоугольного треугольника.
Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
Эти определения применимы только для острых углов (от 0º до 90°).
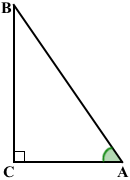
в треугольнике ABC, где ∠C=90°, BC — катет, противолежащий углу A, AC — прилежащий к углу A катет, AB — гипотенуза.
В курсе алгебры 10 класса вводятся определения синуса, косинуса, тангенса и котангенса для любого угла (в том числе, отрицательного).
Рассмотрим окружность радиуса R с центром в начале координат — точке O(0;0). Точку пересечения окружности с положительным направлением оси абсцисс обозначим P0.
В геометрии угол рассматривается как часть плоскости, ограниченная двумя лучами. При таком определении величина угла изменяется от 0° до 180°.
В тригонометрии угол рассматривают как результат поворота луча OP0 вокруг начальной точки O.
При этом поворот луча против часовой стрелки договорились считать положительным направлением обхода, по часовой стрелке — отрицательным (это соглашение связано с истинным движением Солнца вокруг Земли).
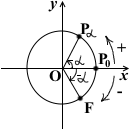
Например, при повороте луча OP0 вокруг точки O на угол α против часовой стрелки точка P0 перейдёт в точку Pα,
при повороте на угол α по часовой стрелке — в точку F.
При таком определении величина угла может принимать любые значения.
Если продолжить вращение луча OP0 против часовой стрелки, при повороте на угол α°+360°, α°+360°·2,…,α°+360°·n, где n — целое число (n∈Ζ), снова попадём в точку Pα:
Углы измеряют в градусах и в радианах.
1° — это угол, равный 1/180 части градусной меры развёрнутого угла.
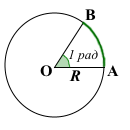
1 радиан — это центральный угол, длина дуги которого равна радиусу окружности:
Обозначения радиана обычно не пишут. Обозначение градуса в записи пропускать нельзя.
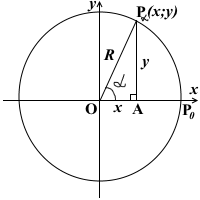
Точка Pα, полученная из точки P0 поворотом луча OP0 вокруг точки O на угол α против часовой стрелки, имеет координаты Pα(x;y).
Опустим из точки Pα перпендикуляр PαA на ось абсцисс.
В прямоугольном треугольнике OPαA:
PαA — катет, противолежащий углу α,
OA — катет, прилежащий к углу α,
По определению синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике имеем:
Таким образом, в случае окружности с центром в начале координат произвольного радиуса синусом угла α называется отношение ординаты точки Pα к длине радиуса.
Косинусом угла α называется отношение абсциссы точки Pα к длине радиуса.
Тангенсом угла α называется отношение ординаты точки Pα к её абсциссе.
Котангенсом угла α называется отношение абсциссы точки Pα к её ординате.
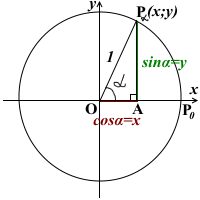
Поэтому удобно выбрать R=1.
Окружность с центром в начале координат и радиусом R=1 называется единичной.
1) Синусом угла α называется ордината точки Pα(x;y) единичной окружности:
2) Косинусом угла α называется абсцисса точки Pα(x;y) единичной окружности:
3) Тангенсом угла α называется отношение ординаты точки Pα(x;y) к её абсциссе, то есть отношение sinα к cosα (где cosα≠0):
4) Котангенсом угла α называется отношение абсциссы точки Pα(x;y) к её ординате, то есть отношение cosα к sinα (где sinα≠0):
Введённые таким образом определения позволяют рассматривать не только тригонометрические функции углов, но и тригонометрические функции числовых аргументов (если рассматривать sinα, cosα, tgα и ctgα как соответствующие тригонометрические функции угла в α радиан, то есть синус числа α — это синус угла в α радиан, косинус числа α — это косинус угла в α радиан и т.д.).
Свойства тригонометрических функций изучаются в курсе алгебры в 10 или 11 классе отдельной темой. Тригонометрические функции широко применяются в физике.
Изучение школьного курса тригонометрии в контексте ФГОС
ГБОУ гимназии № 000 Санкт-Петербурга
Изучение школьного курса тригонометрии в контексте ФГОС
В статье рассматривается роль тригонометрии в развитии мышления школьников, а также ее значимость для дальнейшего образования и практической деятельности.
Задача учителя – открывать новую перспективу размышлениям ученика.
Раздел школьного курса математики «Тригонометрия» неоднократно претерпевал изменения как по содержанию, так и по количеству часов на его изучение. Так, до 1966 года в 9-х и 10-х классах изучалась отдельная дисциплина «Тригонометрия». Изучение курса строилось в той логической последовательности, в которой «осваивало тригонометрические закономерности человечество: от практических измерений – к формальным положениям науки, в полном соответствии с идеей » [1]. Таким образом, с помощью тригонометрии ребенок имел возможность «примерить» на себя математический стиль мышления, просканировать свою предрасположенность, свой интерес к человеческой деятельности такого рода. С реформой тригонометрия перестала рассматриваться как педагогический инструмент развития мышления, приобщения ребенка к основам научной картины мира. И, к сожалению, индуктивный характер изучения тригонометрии стал уступать место формально-логическому. В результате, тригонометрический материал стал постепенно «выжиматься» не только из основной школы, но и из курса старшей ступени.
Сейчас, с одной стороны, возвращается прежний, разумный порядок ее изучения: в основной школе изучается тригонометрия треугольника, а в средней школе тригонометрия составляет целостный раздел курса алгебры и начал анализа, с другой стороны, при том количестве часов, которое уделяется на эту тему, ученикам не хватает времени на вдумчивое и глубокое ее освоение.
В то же время тригонометрический материал входит в ЕГЭ и используется при проведении всевозможных олимпиад и конкурсов. Соответственно не снижается потребность определенной части учащихся в глубоком знании тригонометрии.
Поэтому так важна методически грамотная организация изучения данного раздела, способствующая формированию универсальных учебных действий учащихся – одной из целей ФГОС второго поколении, в которых наряду с предметными выделяются также метапредметные и личностные образовательные результаты.
Для достижения необходимых результатов использую в своей работе системно-деятельностный подход. Учу своих учеников отвергать «знания, приобретенные путем простого зубрения», и приветствовать «умственный материал, набираемый памятью постепенно, день за днем, в связи с различными контекстами, связанный ассоциативно с другими внешними событиями и неоднократно подвергшийся обсуждению» [2]. Активно использую на уроках исторические сведения, так как «экскурсы в историческое прошлое оживляют урок, дают разрядку умственному напряжению, поднимают интерес к изучаемому материалу и способствуют прочному его усвоению» [3].
Практика показывает, что основная проблема изучения тригонометрии в школе связана с освоением идеи «числовой окружности» и введением тригонометрических функций числового аргумента. Считаю, что в школьной программе не уделяется должного внимания освоению идеи единичной окружности, а практическое решение проблемы доверяется учителю, его методическому «чутью».
Убеждена, что преподавателю необходимо так организовать изучение материала, чтобы у учащихся возникли отчетливые геометрические представления, связанные с единичным кругом. Это требование может показаться, на первый взгляд, усложнением задачи преподавания, однако затраченное время с избытком окупится позже.
Второй этап – изучение темы «Элементы тригонометрии» (алгебра, 9 класс). Согласна с точкой зрения об индуктивном изучении тригонометрии. Поэтому основную цель освоения данной темы вижу в плавном переходе к тригонометрии любого угла. И снова особое место отвожу изучению «тригонометрического» круга, так как воспроизведение его мысленно или на бумаге и знание теоремы Пифагора закладывают основу не только теории тригонометрии острого угла, но и теории тригонометрических функций любого действительного аргумента. В результате ученик получает возможность непосредственно увидеть справедливость изученных формул тригонометрии. В противном случае, он обречен на заучивание всех этих формул без достаточной мнемонической основы и оказывается в беспомощном положении, если та или иная формула ускользает из его памяти.
Остановлюсь более подробно на описании действий, направленных на решение указанной задачи в рамках двух тем. При изучении темы «Понятие угла» учащиеся учатся отмечать на пересечении единичной окружности и осей координат «опорные» точки, соответствующие углам 0̊, 90̊, 180̊, 270̊; потом точки, соответствующие углам 45̊, 135̊, 225̊,315̊ (получаемые делением пополам координатных углов); затем точки, получаемые делением пополам вертикальных радиусов единичной окружности (30̊, 150̊, 210̊, 330̊), и, наконец, точки, получаемые делением пополам горизонтальных радиусов единичной окружности (60̊, 120̊, 240̊, 300̊). Изображению точек во втором и в третьем случаях помогает опора на интуитивно ясное свойство синуса острого угла: с увеличением угла от 0̊ до 90̊ значения синуса угла увеличиваются (принимая каждое свое значение только один раз). Учащиеся формулируют выводы: например, так как sin 30̊ = 0,5, то если на рисунке изображен острый угол, «синус» которого равен 0,5, этот угол содержит 30̊. Затем десятиклассникам предлагаются небольшие самостоятельные работы, результаты которых напрямую зависят от тщательной отработки изучаемого материала. Так как материал излагается с опорой на ранее изученное, то у учащихся появляется возможность получить хорошие отметки за большое число несложных, но важных работ.
При изучении темы «Радианная мера угла» ученики обычно недопонимают необходимость выражать число радиан через число «пи». Чтобы снять всякие сомнения на этот счет, вместе с учениками откладываем углы в 1, 2, 3, 4, 5, 6 радиан (при этом необходимо откладывать 1, 2, 3, 4, 5, 6 раз дугу, равную ее радиусу). Эмпирическим путем получаем: ни одно новое деление не совпадет со старым. Таким образом, становится ясно, что число 



В итоге, можно надеяться на успешное решение простейших тригонометрических уравнений, так как умение правильно изображать на единичной окружности точки, соответствующие «табличным» значениям тригонометрических функций, должно быть сформировано.
В заключение хочется отметить, что учащиеся, независимо от профиля школы, должны получить опыт «создания» фрагмента науки. А тригонометрия для этого является наиболее естественным разделом школьной математики. И поэтому каждый учитель математики должен определить свое отношение к этим возможностям тригонометрии.
2. Подласый : Новый курс: учеб. для студ. пед. вузов: в 2 кн. М.: Гуманист: Владос, 2000. – кн.1: Общие основы. Процесс обучения. – С.36.
3. Малыгин историзма в преподавании математики в средней школе. – М.: «Учпедгиз», 1956. – С. 3.
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Один из подходов к изучению тригонометрии в 10-м классе
Разделы: Математика
Еще в 1905 г. русские читатели могли прочесть в книге Уильяма Джеймса “Психология” его рассуждения о том, “почему зубрение представляет такой дурной способ учения?”
“Знания, приобретенные путем простого зубрения, почти неизбежно забываются совершенно бесследно. Наоборот, умственный материал, набираемый памятью постепенно, день за днем, в связи с различными контекстами, связанный ассоциативно с другими внешними событиями и неоднократно подвергший обсуждению, образует такую систему, вступает в такую связь с остальными сторонами нашего интеллекта, легко возобновляется в памяти массою внешних поводов, что остается надолго прочным приобретением”.
С тех пор прошло более 100 лет, а слова эти поразительно остаются злободневными. В этом каждодневно убеждаешься, занимаясь со школьниками. Массовые пробелы в знаниях настолько велики, что можно утверждать: школьный курс математики в дидактическом и психологическом отношениях – не система, а некое устройство, поощряющее кратковременную память и нисколько не заботиться о памяти долговременной.
Знать школьный курс математики – значит владеть материалом каждого из направлений математики, быть в состоянии актуализировать любое из них в любое время. Чтобы достичь этого, нужно систематически обращаться каждому из них, что порой не всегда возможно из-за сильной загруженности на уроке.
Есть другой путь долговременного запоминания фактов и формул – это опорные сигналы.
Тригонометрия – один из больших разделов школьной математики, изучаемой в курсе геометрии 8, 9 классов и в курсе алгебры 9 класса, алгебры и начал анализа в 10 классе.
Самый большой объем изучаемого материала по тригонометрии приходится на долю 10 класса. Большую часть этого материала из тригонометрии можно изучить и запомнить на тригонометрическом круге (окружность единичного радиуса с центром в начале прямоугольной системы координат). Приложение1.ppt
Рассмотрим изучение этих понятий на тригонометрическом круге.
1) Определение синуса, косинуса, тангенса и котангенса.
После введения понятия тригонометрического круга (окружность единичного радиуса с центром в начале координат), начального радиуса (радиус окружности по направлению оси Ох), угла поворота, учащиеся самостоятельно получают определения для синуса, косинуса, тангенса и котангенса на тригонометрическом круге, используя определения из курса геометрии, то есть, рассматривая прямоугольный треугольник с гипотенузой, равной 1.
Косинусом угла 
Синусом угла 
2) Радианное измерение углов на тригонометрическом круге.
После введения радианной меры угла (1 радиан – это центральный угол, которому соответствует длина дуги, равная длине радиуса окружности), учащиеся делают вывод, что радианное измерение угла – это числовое значение угла поворота на окружности, равное длине соответствующей дуги при повороте начального радиуса на заданный угол. 
Тригонометрический круг разделен на 12 равных частей диаметрами окружности. Зная, что угол 


А радианные измерения углов, кратных
3) Область определения и область значений тригонометрических функций.
Будет ли соответствие углов поворота и значений координат точки на окружности функцией?
Каждому углу поворота соответствует единственная точка на окружности, значит данное соответствие – функция.
Получаем функции
Введем понятия линий тангенсов и котангенсов на тригонометрическом круге.
1) Пусть 
2) Аналогично получаем линию котангенсов. Пусть у=1, тогда 
На тригонометрическом круге без труда можно определить область определения и область значений тригонометрических функций:
4) Значения тригонометрических функций на тригонометрическом круге.
Значит по определению синуса, косинуса, тангенса, котангенса можно определить значения для углов кратных 

Табличные значения синуса и косинуса расположены на соответствующих осях следующим образом:
5) Периодичность тригонометрических функций.
На тригонометрическом круге видно, что значения синуса, косинуса повторяются через каждые 

6)Четность и нечетность тригонометрических функций.
Это свойство можно получить, сравнивая значения положительных и им противоположных углов поворота тригонометрических функций. Получаем, что
Значит, косинус – четная функция, все остальные функции – нечетные.
 |  |
7) Возрастание и убывание тригонометрических функций.
По тригонометрическому кругу видно, что функция синус возрастает 
Аналогично рассуждая, получаем промежутки возрастания и убывания функций косинуса, тангенса и котангенса.
8) Формулы приведения.
За угол 
Алгоритм применения формул приведения:
1) Определить знак функции при повороте на заданный угол.
При повороте на угол 

9) Значения обратных тригонометрических функций.
Введем обратные функции для тригонометрических функций, пользуясь определением функции.
Алгоритм нахождения значений обратных тригонометрических функций:
1) нахождение на соответствующей оси значения аргумента обратной тригонометрической функции;
2) нахождение угла поворота начального радиуса с учетом области значений обратной тригонометрической функции.
Например:
10) Решение простейших уравнений на тригонометрическом круге.
Чтобы решить уравнение вида 

Для уравнения 

Аналогично для уравнений вида 

 | |
 |  |
11) Решение неравенств.
Чтобы решить неравенства вида 

Чтобы решить неравенства вида 

Чтобы решить неравенства вида 

Аналогично для неравенств с котангенсом.
Необходимо практиковать чтение промежутков на тригонометрическом круге, тогда решения неравенств определяются безошибочно.
12) Основные формулы тригонометрии.
1) Основные тригонометрические тождества.
Очевидны выводы формул 
2) Формулы сложения выводятся с использованием скалярного произведения векторов начального и “конечного” радиусов.
 |  |
Другие формулы сложения получаются с использованием предыдущей, формул приведения и свойств четности и нечетности тригонометрических функций.
Почти все формулы тригонометрии являются следствиями этих основных формул.
Все понятия и формулы тригонометрии получают сами ученики под четким руководством учителя с помощью тригонометрического круга. В дальнейшем этот “круг” будет служить для них опорным сигналом или внешним фактором для воспроизведения в памяти понятий и формул тригонометрии.