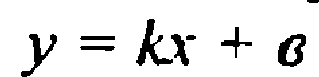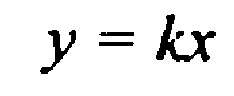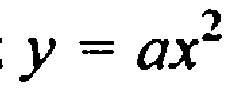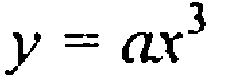в каком классе изучают функции и графики

Алгебра. 8 класс

График функции – понятие в математике, которое даёт представление о геометрическом образе функции.

Общее определение функции

Пусть K – некоторое множество чисел и пусть каждому числу x из множества K в силу определённого закона (зависимости) поставлено в соответствие одно число y из множества T.

Тогда говорят, что y – это функция от x, определённая на множестве K.

x называют независимой переменной, или аргументом.
y называют зависимой переменной, или функцией.
K – множество возможных значений аргументов, или область определения функции.

y = f(x), где f – это правило, или зависимость, по которому значению x, или аргументу, ставится в соответствие значение y, или значение функции.

Значение y₀, соответствующее числу x₀ для данной функции y(x) называют значением этой функции в точке x₀ и обозначают y(x₀) или f(x₀).

Возможные записи
y = 3x
y(1) = 3, или f(1) = 3
y(2) = 6, или f(2) = 6 и так далее.

Множество всех значений y, которые может принимать функция на заданной области определения, называют областью значений функции.

Чтобы задать функцию, нужно задать правило, или зависимость, с помощью которой по определённому значению аргумента можно найти соответствующее значение функции.

Способы задания функции

Задание функции при помощи формулы

Задание функции при помощи таблицы

Так, на множестве чисел от 1 до 10 будет определён закон, по которому каждому значению t будет соответствовать определённое значение курса евро.

Задание функции при помощи графика

График изменения курса валют

Задана декартова система координат.
x – это ось значений времени, т. е. ось дат.
y – это ось значений курса евро.

Каждая упорядоченная пара чисел задаст на координатной плоскости точку. Последовательно соединив эти точки, мы увидим закон или правило, по которому в зависимости от даты изменялся курс евро.

Данный график изменений курса евро представляет собой непрерывную линию. Такую функцию называют непрерывной. Т. е. курс евро при непрерывном значении t изменяется непрерывно, без больших скачков (в математическом смысле).

Функция является непрерывной, когда малому изменению (или приращению) аргумента соответствуют малые изменения (приращения) функции.

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.

Источник

Основные виды функций, изучаемых в курсе «Алгебра» за 7кл

Содержимое разработки

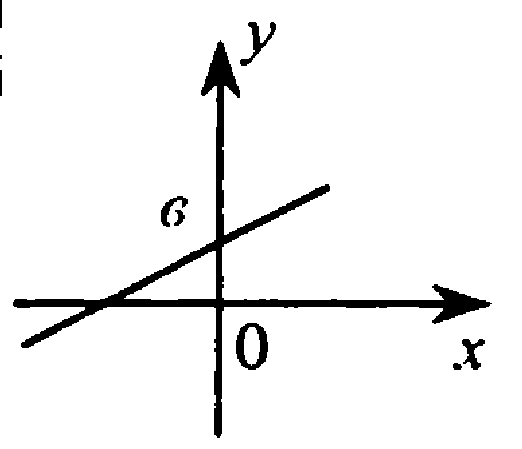
Прямая не проходящая через начало координат, достаточно 2 точек.

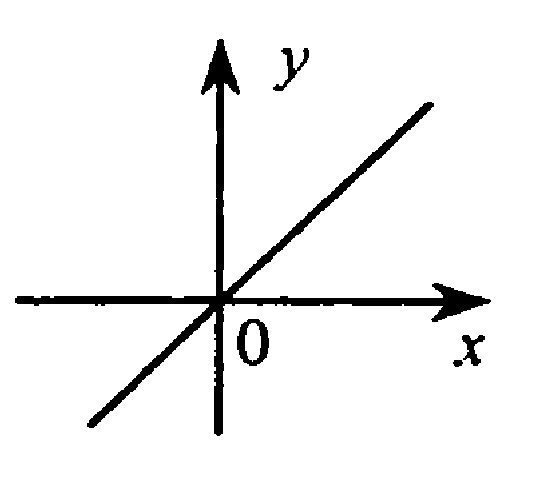
Прямая проходящая через начало координат, достаточно 2 точек.

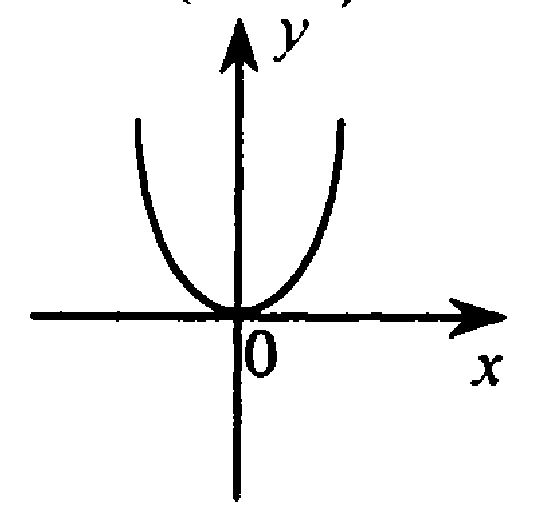
Парабола, достаточно 5 точек, две полож нуль и две отриц.

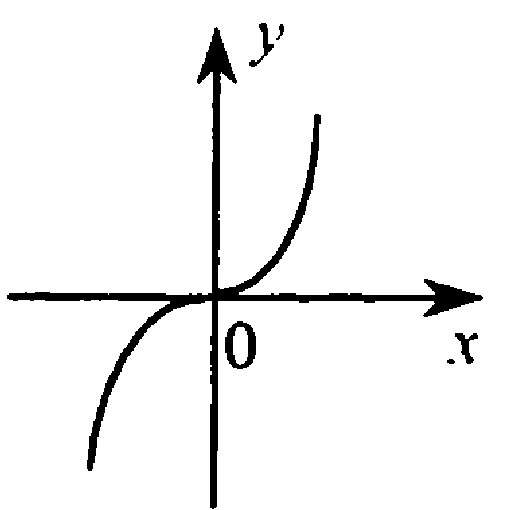
достаточно 5 точек, две положительные нуль и две отриц.

Точка О(0;0) не принадлежит графику

Точка О(0;0) принадлежит графику

Точка О(0;0) принадлежит графику

Точка О(0;0) принадлежит графику

k 0, из 1 в 3 четверть

а0, из 1 в 3 четверть

Относительно оси y.

Относительно начала координат.

Часто задаваемые вопросы

— Условие пересечения графиков двух линейных функций?

-Условие параллельности графиков двух линейных функций?

Проверьте принадлежит ли точка графику функции у=5х+3?

Не принадлежит, если верно, то принадлежит.

Как найти координаты точек пересечения функции с осями? Если с осью Х –то нулим «у», если с осью Y, то нулим «х».

Как найти точки пересечения графиков функций? Графически или аналитически (прировнять правые чести и решить уравнение, найти вторую координату)

Источник

План-конспект урока алгебры на тему «Функции, их графики и свойства»

Разделы: Математика

Образовательная цель: Обобщить знания об изученных функциях и их свойствах. Рассмотреть применение функций в различных областях знаний. Проверить усвоение учащимися данной темы.

Развивающая цель: Развивать мыслительную деятельность, творческие способности и логическое мышление учащихся.

Воспитательная цель: воспитывать познавательную активность, культуру общения, прививать интерес к предмету

Тип урока: обобщение знаний

I. Организационный момент. Сообщение темы и цели урока.

— Ребята, мне попалась на глаза интересная задача. Подумайте, можно ли по её условию составить уравнение.

Если шофёру господина министра 40 лет 3 месяца и 12 дней, а мост в городе Квебек в Канаде имеет длину 577 метров, то на скольких желтках нужно замесить лапшу, чтобы накормить 6 человек различного возраста, если принять во внимание, что ширина полотна на железных дорогах Боснии составляет 0, 7 метра?

— Можно ли по условию задачи составить уравнение? (безусловно, нет)

— Почему? (Потому что величины, входящие в условие задачи, никак между собой не связаны. Ни одна из них, как мы говорим, не является функцией от другой).

— Вот сегодня на уроке мы обобщим знания, связанные с понятием функции, рассмотрим примеры задач из различных областей знаний, связанных с функциями, и проверим уровень усвоения материала темы.

— А что же такое функция?

На доске прикрепляется надпись “Определение функции”.

— А вы знаете, что слово “функция” (от латинского function – исполнение, осуществление) в математике впервые употреблено немецким математиком В.Г.Лейбницем. Но сами функции и способы их задания фактически изучались людьми очень давно.

Знаменитый древнегреческий историк Геродот в 425 году до нашей эры писал, что египетские цари, разделив землю между египтянами, брали ежегодный налог, пропорциональный площади занимаемого участка. Конечно, ни египетские цари, ни землевладельцы, ни сам Геродот не произносили слова “функция”, но ведь речь идёт о том, что каждому значению площади соответствовало некоторое значение налога.

Хотя в древности функций не знали, но явления, которые мы сегодня описываем с их помощью, давно известны людям.

— Какие ещё понятия связаны с понятием функции?

(Даются определения: зависимая переменная, независимая переменная, область определения, множества значений функции, график функции).

2. Способы задания функции.

На доске прикрепляется надпись “Способы задания функции”.

— Какими способами может задаваться функция? (табличный, графический, словесный, аналитический).

— Сейчас внимательно послушайте математический софизм о том, как ученик, используя аналитический и табличный способы задания функции, построил их графики и найдите ошибку.

Математический софизм (рассказывает ученик, получивший предварительное задание).

Ученику было предложено построить графики функций:

Используя аналитическое задание, он построил таблицы значений для некоторых значений аргумента.

По полученным таблицам построил схематические графики функций.

Ученик получил одинаковые графики и сделал вывод, что равенство x 3 = 4x является тождеством.

Б). Рассмотрим словесный способ задания функции.

Каким уравнением задаётся такая функция? Как выглядит её график?

— Мы рассмотрели понятие функции, способы задания функции, а сейчас вспомним изученные функции и их свойства.

3. Функции и их свойства.

-Какие функции мы с вами изучили?

А). Прямая пропорциональность.

На доске прикрепляется надпись “y=kx”.

— Какая функция называется прямой пропорциональностью?

— Как называется число k?

— Как ведёт себя функция в зависимости от знака k? От числового значения k?

— Прямая пропорциональность имеет конкретный практический смысл. Приведите примеры прямопропорциональных величин.

Вывод. Совершенно разные явления, взаимодействия между величинами описываются одной и той же функцией.

Б). Линейная функция

На доске прикрепляется надпись “”.

— Опишите свойства функции по плану.

Исследовательская работа в парах.

— Даны кусочно-заданные функции. Провести исследование функций, ответить на вопросы.

— Назвать область определения функции f(x);

— Назвать множество значений функции g(x);

— Решить уравнение g(x)=0;

— Решить уравнение f(x)=g(x);

— При каких значениях аргумента функция g(x) принимает отрицательные значения?

— Сравнить числовые коэффициенты прямых, образующих графики f и g на отрезках и .

В). Квадратичная функция.

— Какая функция называется квадратичной?

На доске прикрепляется надпись “”.

— Опишите свойства функции по плану.

Работа с графиками функций.

— Какой график соответствует каждому движению?

Функция зависимости тормозного пути автомобиля от скорости движения задаётся формулой:

, где S – тормозной путь, m – масса автомобиля, F – сила трения, V – скорость автомобиля.

Используя графики функций ответитьте на вопросы:

Чему равен тормозной путь автомобиля при скорости 40 км/ч в каждом случае?

Какую дистанцию нужно соблюдать двум автомобилям, движущимся при дожде со скоростью 60 км/ч?

На каком наименьшем расстоянии от вас должен находиться автомобиль, движущийся со скоростью 40 км/ч, для того, чтобы вы могли безопасно перейти дорогу в гололёд?

Вывод. Даже в такой житейской ситуации, как переход

дороги в гололёд, нам окажет помощь квадратичная функция и её график.

Г). Обратная пропорциональность.

— Какая функция называется обратной пропорциональностью?

На доске прикрепляется надпись “”.

— Опишите свойства функции по плану.

— Где в жизни мы встречаемся с обратно пропорциональной зависимостью?

— Ещё интересен такой факт. Из физики вы знаете, что тело, брошенное под углом к горизонту, летит по параболе. Но если придать ему начальную скорость V₀ в пределах 7,9 12 км/c, но тут уж оно будет двигаться по гиперболе.

Вывод. Таким образом, функции нужно знать, чтобы лучше изучить и использовать законы природы, окружающего мира.

Самостоятельная работа. Тест.

В каких четвертях располагается график функции :

Как ведёт себя график функции:

в) возрастает и убывает.

Найдите ординату точки, ограничивающей функцию снизу:

4. Найдите координаты вершины параболы функции :

5. Найдите наибольшее значение функции на луче :

Ветви какой из парабол направлены вниз:

а) ;

б) ;

в) ;

г)

Найдите координаты вершины параболы, заданной формулой :

Задайте уравнениями графики функций:

IV. Итог урока. Рефлексия деятельности учащихся.

— Что нового узнали на уроке?

— Что особенно понравилось?

— Оцените свою работу на уроке, учитывая полученные оценки.

V. Домашнее задание.

— А сейчас послушайте отрывок из сказки “Спящая красавица” и постарайтесь ответить на вопрос.

Вот фея предстала перед принцем, взмахнула палочкой… раз и готово! И появился…, нет, не мост, а старый потрёпанный пергамент, на котором были записаны несколько функций:

В какой из функций скрыт мост?

Источник

Алгебра

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Понятие функции

Понятие функции в школьной программе впервые встречается в 7 классе, поэтому настоятельно рекомендуем перечитать посвященный этой теме урок. Напомним, что функцией (в учебной литературе может использоваться сокращение ф-ция) называется соответствие между элементами двух множеств или, другими словами, зависимость между двумя величинами. Чаще всего в алгебре рассматриваются числовые ф-ции, которые заданы аналитически, то есть формулой. В качестве примера можно привести запись

Здесь х – это независимая переменная, или аргумент, а у – зависимая величина, или просто функция. Принципиально важно, что каждому значению аргумента соответствует только одно значение зависимой величины. Часто в математике используют запись

Она читается как «игрек равен эф от икс» и означает, что величина у как-то зависит от х. По сути, она равноценна записи

Если в скобках стоит конкретное число, то запись означает значение ф-ции при этом значении аргумента.

У каждой ф-ции есть область допустимых значений (используется сокращение ОДЗ), или область определения функции. Это те значения аргумента, при которых ф-ция определена. Здесь возможны два случая. В первом область определения указывается прямо. Например, если рассматривается функция у = х 4 при значениях х от 1 до 3, то и областью определения будет всё множество чисел от 1 до 3. Для обозначения области определения используется запись D(y) или D(f). При изучении неравенств мы уже познакомились с такими объектами, как числовые промежутки. Именно с их помощью указывают ОДЗ.

Пример. Постройте график функции у = х, если D(y) = [– 3; 4].

Решение. Ф-ция у = х – это линейная функция, мы уже умеем строить их графики (они представляют собой прямую линию). Выглядеть он будет так:

Однако в условии также есть запись D (y) = [– 3; 4], которая означает, что ф-ция определена только при х от – 3 до 4. С учетом этого условия график несколько преобразится:

Грубо говоря, часть графика, которая не входит в область определения, просто «отрезана».

Значительно чаще область определения явно не указывается. В этом случае предполагается, что ф-ция определена во всех точках числовой прямой, в которых ее вообще возможно вычислить. Например, ф-цию у = 9х 3 – 47 можно вычислить при любом значении х, поэтому ее область определения – вся числовая прямая, то есть D(y) = (– ∞; + ∞).

А когда же вычислить функцию невозможно? К этому уроку нам известны две таких ситуации:

Например, вычислить ф-цию у = 5/х при х = 0 невозможно, поэтому ее область определения – вся числовая прямая, кроме нуля, то есть

имеет область определения D(y) = [5; + ∞), так как при х 2 при D(y) = [– 2; 2] областью значений будет промежуток [0; 4], то есть Е(у) = [0; 4]. Это видно из графика функции:

Ещё раз напомним, что область определения и область значения функции указываются с помощью числовых промежутков.

Теперь перейдем к тем понятиям, которые не изучались ранее. Первое из них – это нули функции. Так называют те значения аргумента, при которых функция обращается в ноль.

есть два нуля, х = 4 и х = 5. Убедиться в этом можно подстановкой:

у(4) = 4 2 – 9•4 + 20 = 0

у (5) = 5 2 – 9•5 + 20 = 0

Для нахождения нулей ф-ции у = f(x) надо просто решить уравнение

Например, чтобы найти нули приведенной выше функции

надо решить уравнение

Сделаем это, ведь мы уже умеем решать квадратные уравнения:

На графике нули ф-ции – это те точки, в которых график пересекает ось Ох:

Ещё одно новое понятие – промежутки знакопостоянства. Так называют промежутки числовой прямой, на которых ф-ция либо только положительна, либо только отрицательна. Для наглядности покажем их на графике:

Пусть есть ф-ция у = f(x). Для нахождения промежутков знакопостоянства необходимо решить неравенства f(x)>0 и у = f(x) 0:

Получаем, что функция положительна на промежутке (12; + ∞).

Аналогично решив неравенство 3х – 36 2 – 5х. Найдите такое значение величины а, для которого выполняется условие у(а) = у(а + 2).

Решение. Очевидно, что у(а) = а 2 – 5а. Теперь вычислим у(а + 2):

у(а + 2) = (а + 2) 2 – 5(а + 2) = а 2 + 4а + 4 – 5а – 10 = а 2 – а – 6.

Теперь приравняем значения у(а) и у(а + 2):

а 2 – 5а = а 2 – а – 6

а 2 – 5а – а 2 + а = – 6

Убедимся, что мы нашли требуемое значение а:

у(1,5) = 1,5 2 – 5•1,5 = 2,25 – 7,5 = – 5,25

у(1,5 + 2) = у(3,5) = 3,5 2 – 5•3,5 = 12,25 – 17,5 = – 5,25

Растяжение и сжатие графиков функций

Пусть на координатной плоскости есть точка А с координатами (х₀; у₀). Куда переместится эта точка, если ее ордината (то есть у₀) увеличится, например, в два или в три раза? Она отодвинется от оси Ох. Если же ее ордината уменьшится, то точка приблизится к оси. Наконец, если ордината поменяет знак, то точка, изначально, лежащая выше оси, окажется ниже её. Проиллюстрируем это на картинке:

Пусть есть пара функций у(х) и g = k•у(х), где k– какое-то постоянное число (константа), не равная нулю. Примерами таких пар являются:

Посмотрим, как связаны графики таких функций. На рисунке красным цветом показана функция у(х), а синим g = 2у(x):

При любом значении аргумента выполняется условие g(х) = 2у(х). Это значит, что ордината (координата у) каждой точки графика g(х) вдвое больше, чем ордината соответствующей точки графика у(х). В частности, отрезок АА₂ вдвое длиннее отрезка АА₁:

Аналогично можно записать, что

Таким образом, график g(x) выглядит так, будто бы график у(х) «растянули» в 2 раза. Каждая точка «переезжает» на новое место, сдвигаясь по вертикали. Так, если точка А₁ имела координаты (– 6; 2), то при растяжении графика функции она получит координаты (– 6; 4), то есть ее координата у увеличится вдвое. Точка B₁ имела координаты (2; – 2), а в графике g(х) занимает позицию (2; – 4).

Убедимся в этом на примере ф-ций у = х 2 и g = 2х 2 :

В общем случае говорят, что график функции g(х) = ky(x) получается растяжением графика у(х) в k раз.

Пример. Функция у(х) задана графически:

Постройте график функции g(х) = 3у(х).

Решение. Каждую точку отодвинем от оси Ох, увеличив координату у точек в 3 раза:

При сжатии графика каждая точка параболы приближается к оси Ох, при этом ордината точек уменьшается вдвое. Так, точка А₂ с координатами (3; 9) переходит в точку А₁ с координатами (3; 4,5).

Отдельно стоит рассмотреть случай, при котором коэффициент k является отрицательным. В этом случае график отображается симметрично относительно оси Ох. Те точки, которые имели изначально положительную ординату и находились выше Ох, в результате получают отрицательную ординату и оказываются ниже оси Ох. Покажем на рисунке графики ф-ций у = х 2 и у = – х 2 (то есть k =– 1):

Если же, например, коэффициент k = – 2, то надо и растянуть график, и перевернуть его относительно оси Ох. В частности, так выглядит график у = – 2х 2 :

Параллельный перенос графиков функций

Теперь посмотрим, как передвинется отдельная точка на координатной плоскости, если к ее ординате добавить какое-нибудь число. Если это число положительное, то точка поднимется выше, а если отрицательное, то она опустится:

Это означает, что если к какой-нибудь функции добавить некоторое число, то график функции переместится вверх или вниз. Для примера построим графики функций у = х 2 + 2 и у = х 2 – 5:

Параллельный перенос возможен не только в вертикальном, но и в горизонтальном направлении. Для такого перемещения надо изменить абсциссу точки, а не ординату:

Аналогично может сдвинуться не только точка, но и целый график функции. Если вместо аргумента х подставить в ф-цию величину (х +n), то график сместится на n единиц влево.

у(0) = 0 2 = 0 и g(– 3) = g(– 3 + 3) 2 = 0 2 = 0

у(– 1) = (– 1) 2 = 1 и g(– 4) = g(– 4 + 3) 2 = (– 1) 2 = 1

у(– 2) = (– 2) 2 = 4 и g(– 5) = g(– 5 + 3) 2 = (– 2) 2 = 4

Точка А₁ сдвинулась влево на 3 единицы и перешла в точку А₂. Аналогично точка В₁ отобразилась в точку В₂.

Пусть в общем случае есть функции у = у(х) и g(x) = у(х +n), где n – некоторое постоянное число. Значение у(х) в точке х₀ обозначается как у₀. Теперь найдем значение g(x) в точке (х₀ – n):

Получили, то же самое значение, что и у у(х). Покажем это на рисунке:

Рассмотрим теперь случай, когда график сдвигается вправо. Для этого из аргумента исходной функции надо вычесть какое-то число. На рисунке показаны графики функций у = 2х и у = 2(х – 4):

Каждая точка исходного графика (например, А₁) «переехала» на 4 единицы вправо.

Надо понимать, что иногда один график можно получить из другого в несколько переходов. Пусть надо построить график у = – (х – 4) 2 + 5. Его можно получить из обычной параболы у = х 2 в три шага.

Последний шаг – это построение графика у = – (х – 4) 2 + 5. Его можно получить, подняв предыдущий график на 5 единиц вверх:

Гипербола и обратная пропорциональность

Найдем область определения функции у = 1/х. Ясно, что аргумент не может равняться нулю, так как иначе получим деление на ноль:

При любых других значениях х значение у вычислить можно, а потому областью определения будет промежуток (– ∞; 0)⋃(0;+ ∞).

При положительных значениях аргумента ф-ция также будет положительной:

При отрицательных х величина у будет становиться отрицательной:

Это означает, что график ф-ции будет располагаться в I и III четвертях.

Можно заметить, что чем больше х, тем ближе у к нулю:

И наоборот, чем ближе х к нулю, тем больше у:

При этом у не может равняться нулю. Действительно, дробь равна нулю только тогда, когда ее числитель равен нулю. Однако варьируя х, мы меняем только знаменатель, а в числителе остается единица. Поэтому областью значений функции у = х – 1 является промежуток (– ∞; 0)⋃(0;+ ∞).

Для построения графика найдем некоторые точки графика и занесем их в таблицу. Мы построим две таблицы – одну для положительных х, другую для отрицательных:

Теперь можно посмотреть и на сам график:

Первое, что бросается в глаза – это то, что график не представляет собой единую, непрерывную линию. Он разбит на две ветви, одна из которых располагается в III четверти, а другая – в I четверти. Такой «разрыв» связан с тем, что ноль не входит в область определения ф-ции.

Также можно заметить симметричность графика. Действительно, одна из ветвей является симметричным отображением второй ветви.

Построенный нами график называется гиперболой.

На координатной плоскости есть две прямые линии, к которым гипербола приближается, но при этом он не касается их. Это оси Ох и Оу. Для наглядности покажем их штриховой линией:

В математике подобные линии называют асимптотами функции. Горизонтальная асимптота прямая соответствует линии х = 0, а вертикальная асимптота линии у = 0.

Зная, как выглядит график у = 1/х, мы можем построить и другие, схожие с ним графики для ф-ций у = k/х, где k– это некоторое число. Их можно получить из гиперболы, используя сжатие и растяжение графиков. Если коэффициент k больше единицы, то график «отдаляется» от осей Ох и Оу:

Все эти линии являются примерами гипербол. Если коэффициент k отрицательный, то графики переворачиваются относительно оси Ох и занимают II и IV четверти:

Все приведенные зависимости вида у = k/х называют обратными пропорциональностями.

Примерами обратной пропорциональности являются ф-ции:

Обратная пропорциональность очень часто встречается в жизни. Так, время, затрачиваемое на поездку на автомобиле, обратно пропорционально средней скорости движения. Количество товара, которое можно купить на одну зарплату, обратно пропорционально стоимости этого товара.

Дробно-линейная функция

Теперь рассмотрим несколько более сложные ф-ции, чьи графики, однако, также представляют собой гиперболу. Пусть есть ф-ция вида

Как будет выглядеть ее график? Для ответа на этот вопрос выполним преобразование:

Здесь мы в числителе и знаменателе добавили и сразу вычли слагаемое 2.Этот прием помог нам выделить целую часть из дроби. В результате мы получили ф-цию, график которой можно получить с помощью двух параллельных переносов графика у = 6/х. Сначала график сместится на две единицы вправо:

На следующем шаге график поднимется на единицу вверх:

Стоит обратить внимание, что при таком передвижении гиперболы передвигаются и асимптоты графика гиперболы:

представляет собой дробь, являющуюся отношением двух линейных многочленов, х + 3 и х – 2. В математике подобные ф-ции называют дробно-линейными функциями. В качестве примеров дробно-линейных функций можно привести:

Из любой дробно-линейной функции можно выделить целую часть. Покажем это на нескольких примерах:

Во всех этих случаях график дробно-линейной функции можно построить с помощью двух параллельных переносов гиперболы.

Однако есть одно исключение. Иногда при выделении из дроби целой части дробной части не остается вовсе, то есть линейные полиномы можно сразу сократить. Например:

Графиком таких функций являются прямые горизонтальные линии. Однако на них должна быть одна «исключенная». Действительно, пусть надо построить график ф-ции

Проведя преобразования, получим

то есть у = 2. Однако в знаменателе дроби не может стоять ноль. Если же подставить в дробь х = – 2, то получим деление на ноль:

Поэтому график ф-ции будет выглядеть так:

Итак, по итогам урока мы узнали:

Источник