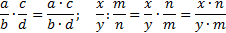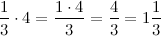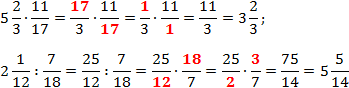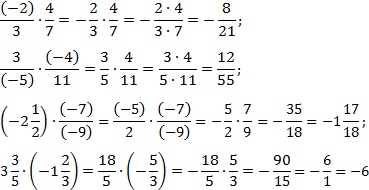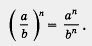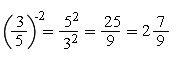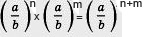в каком классе изучают десятичные дроби по математике
Математика 5 класс темы уроков
По математике в 5 классе темы уроков будут посвящены сложению и вычитанию, умножению, делению натуральных чисел. Далее переходят к изучению дробных чисел с акцентом на десятичных дробях. Рассматривают сложение, умножение, округление, сопоставление, деление, вычитание десятичных дробей.
Кроме того, выделяют время на основы площадей и объёмов, использование инструментов и шкал для измерений веса, расстояний, объёмов. Данный этап имеет огромную ценность для использования математики в повседневной жизни, поэтому подойти к нему надо особенно внимательно.
Натуральные числа
Начнём программу с изучения натуральных чисел. Так будет проще для усвоения последующего материала:
Вычитание и сложение натуральных чисел
На последующих двух этапах изучаются основные методы и законы математики, так что к ним следует отнестись внимательно. Важной темой уроков по математике за 5 класс является то, что можно делать с натуральными числами. Берутся за изучение со сложений и вычислений:
Деление и умножение натуральных чисел
Заканчивают изучение умножением и делением:
Объёмы и площади
Эти знания являются фундаментом для моделирования техники, а также других вещей и явлений. Изучают на примере прямоугольников и параллелепипедов:
Дробные числа
Дроби – самая сложная тема в этом году, так что надо её разбирать, не торопясь, и внимательно. В математике за 5 класс в темы уроков входит исследование различных видов дробей:
Десятичные дроби, их вычитание и сложение
Далее надо научиться использовать дроби в математических вычислениях. А сначала – вычитание и сложение:
Десятичные дроби, деление и умножение
Заканчивают исследование десятичных дробей разбором их деления и умножения:
Инструменты для вычислений и измерений
Эта группа уроков откроет для вас математику как мировую культуру, а также её важность для научно-технического прогресса. Далее проходят различные математические инструменты:
Основы комбинаторики
Последняя тема уроков по математике за 5 класс – комбинаторика. Теоремы сложения и умножения. Применение теорем в реальной жизни. Логика перебора. Парадокс Монти Холла. На этом заканчивается программа.
Заключение
Цель на этом этапе – получить знания для практического применения их в жизни. Данный раздел поможет построить логическое критическое мышление, разовьёт способность мыслить абстрактно. Математика – важнейший инструмент для любой науки, поэтому её надо изучать серьёзно. Знания, которые даются на этом курсе, являются фундаментом для понимания многих процессов в окружающем мире.
Прохождение программы курса математики 5–6-х классов за 1,5 учебных года
Разделы: Математика
Математическое образование в нашей стране получают все школьники, начиная с первого года обучения и до последнего. Само собой разумеется, что лишь небольшая часть обучающихся впоследствии станет сама развивать математику. Но применять математические знания и методы станут все. Очень важно, чтобы учащиеся видели прикладные возможности всех разделов математики и почувствовали значение строгих логических рассуждений для всех видов деятельности.
Как же строится школьный курс математики?
В курсе математики для V-XI кл. с учётом возрастных особенностей выделяются три ступени обучения: V-VI, VII-IX, X-XI классы.
В ходе изучения курса учащиеся развивают навыки вычислений с натуральными числами, овладевают навыками действий с обыкновенными и десятичными дробями, с положительными и отрицательными числами, знакомятся с буквенными выражениями, учатся составлять по условию текстовой задачи несложные линейные уравнения и решать их.
Следует отметить, что в V классе слишком много времени уделяется (по стандартной программе) повторению изученного в начальной школе.
Чтобы преодолеть такое положение вещей, делаются различные попытки, одной из которых является разработанная Г.Г. Левитасом переходная программа. Она рассчитана на изучение курса V-VI классов за один учебный год при пяти часах математики в неделю. Изучение этой программы предложено вести по учебникам Н.Я. Виленкина. При этом в течении каждой четверти программа строится из расчёта один пятиурочный цикл в неделю.
Нами было разработано планирование, рассчитанное на изучение математики в V кл. при четырёх часах в неделю, а в VI кл. при пяти часах в неделю. В пятом классе пятый час в неделю может быть использован учителем на свое усмотрение. В зависимости от уровня математической подготовки учащихся, им могут быть предложены задания развивающего характера или задания на ликвидацию пробелов по изучаемой теме. Программа рассчитана на изучение материала V-VI классов за 1,5 учебных года, и поэтому в VI классе со II полугодия необходимо приступать к изучению материала VII класса.
В рамках V класса изучаются следующие темы: натуральные числа (повторение изученного в начальной школе), обыкновенные и десятичные дроби.
В VI классе: отрицательные и положительные числа, пропорции и проценты, решение уравнений и координатная плоскость.
5 КЛАСС
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА ПО КУРСУ «МАТЕМАТИКА» В 5-КЛАССЕ (ПО ЧЕТВЕРТЯМ).
I четверть 9*4 ч.=З6 ч.
| № уроков | Содержание | Кол-во уроков |
| 1-12 | Действия с натуральными числами. | 12 |
| 13-16 | Свойства действий с натуральными числами. | 4 |
| 17-20 | Решение уравнений. | 4 |
| 21-30 | Решение задач (типа «во ск.», «на ск.», больше-меньше; «на», «в», на движение). | 10 |
| 31 | Подготовка к контрольной работе. | 1 |
| 32 | Контрольная работа №1 | 1 |
| 33-36 | Десятичная система исчисления, меры длины. | 4 |
II четверть 7*4 ч.=28 ч.
| № уроков | Содержание | Кол-во уроков |
| 36-39 | Что такое десятичная дробь. Сравнение десятичных дробей. | 4 |
| 40-43 | Сложение и вычитание десятичных дробей. | 4 |
| 44-46 | Решение уравнений. | 3 |
| 47 | Подготовка к контрольной работе. | 1 |
| 48 | Контрольная работа № 2. | 1 |
| 49-52 | Умножение десятичных дробей. | 4 |
| 53-56 | Деление десятичных дробей. | 4 |
| 57-59 | Решение уравнений. | 3 |
| 60 | Подготовка к контрольной работе. | 1 |
| 61 | Контрольная работа № 3. | 1 |
| 62-63 | Округление десятичных дробей. Прикидка | 2 |
III четверть 10*4 ч.=40 ч.
| № уроков | Содержание | Кол-во уроков |
| 64-66 | Обыкновенная дробь. Сравнение на луче. | 3 |
| 67-68 | Правильные и неправильные дроби. Сравнение с 1. | 2 |
| 69-72 | Признаки делимости. Разложение на простые множители. НОД. | 4 |
| 73-76 | Основное свойство. Сокращение дробей. | 4 |
| 77-80 | Сложение, вычитание и сравнение дробей с одинаковыми знаменателями. | 4 |
| 81 | Подготовка к контрольной работе. | 1 |
| 82 | Контрольная работа №4. | 1 |
| 83-86 | НОК. Приведение к общему знаменателю. | 4 |
| 87-90 | Сравнение, сложение и вычитание дробей с разными знаменателями. | 4 |
| 91-93 | Решение уравнений. | 3 |
| 94 | Подготовка к контрольной работе. | 1 |
| 95 | Контрольная работа №5. | 1 |
| 96-99 | Умножение обыкновенных дробей. | 4 |
| 100-104 | Деление обыкновенных дробей. | 4 |
IV четверть 8*4 ч.=32ч.
| № уроков | Содержание | Кол-во уроков |
| 105-107 | Решение уравнений. | 3 |
| 108 | Подготовка к контрольной работе. | 1 |
| 109 | Контрольная работа №6. | 1 |
| 110-113 | Смешанные числа. | 4 |
| 114-117 | Три задачи на дроби. | 4 |
| 118-121 | Решение текстовых задач (составление уравнений, проценты). | 4 |
| 122 | Подготовка к контрольной работе. | 1 |
| 123 | Контрольная работа №7. | 1 |
| 124-127 | Все действия обыкновенными и десятичными дробями. | 4 |
| 128-134 | Повторение. Итоговая контрольная работа. | 7 |
6 КЛАСС
Из программы 6 класса осталось пройти следующие темы: «Положительные и отрицательные числа», «Решение уравнений», «Координатная плоскость», «Пропорция».
За I четверть изучаются положительные и отрицательные числа, координатная плоскость. Первые уроки четверти посвящаются повторению пройденного в 5 классе.
II четверть начинается с изучения темы: «Решение уравнений», а затем до конца четверти учащиеся занимаются нахождением неизвестного члена пропорции и решают задачи на прямую и обратную пропорциональную зависимость.
С окончанием II четверти заканчивается изучение материала 6-го класса.
В каком классе проходят десятичные дроби?
По сравнению с программой времен СССР дети уже даже к 1 классу идут подготовленные. Есть школы разные и разные уклоны. Если школа с математическим уклоном, то с понятиями дробей детей знакомят на поверхностном уровне уже в третьем классе, а уже в пятом классе они начинают полноценно изучать дроби. Десятичные дроби уже могут дать в четвертом классе, а обычные в пятом. Именно в пятом классе дети учат числитель, знаменатель и т.п.
Моя премянница в третьем классе их проходит. Точнее, пару недель назад прошла. Вместе с обычными дробями.
А я, помнится, дроби раза три проходил. Когда-то в начальной школе, потом в пятом классе, а потом ещё в 7-ом. Может тогда и отличались названия тем уроков, но выглядело все одинаково.
В начальной школе ученики только поверхностно знакомятся с дробями. В 4 классе у них есть тема «задачи на нахождение части от целого и целого по части». Это что-то типа: найти «3/4 от 520» и т.п. Но как такого понятия «дроби» они еще не знают. И только в пятом классе они узнают, что такое знаменатель, числитель и т.д.
Программа меняется часто, то что проходят в России в других странах проходят гораздо позднее. В Швеции в Италии таблицу умножения проходят чуть ли не с шестого класса. А мы учили ее в начальной школе.
В российских школах десятичные дроби начинают изучать в пятом классе. Пока у нас школьная программа сильнее.
Сейчас, когда дети идут в школу, то умеют писать, считать и читать. Поэтому программа, которая была у нас, более взрослого поколения, устаревает. Современные дети начинаются знакомиться с дробями в первом классе (более упрощенный вариант), потом более сложные дроби начинают проходить с третьего класса.
Десятичные дроби проходят на класс раньше, чем обыкновенные.
Отмечу, что в четвертом-пятом классах начинают уже решать с ними примеры, а вот понятие дробей могут давать раньше.
Да что говорить, мою племяшку еще в детском садике обыкновенным дробям учили, а они, в общем-то, от десятичных отличаются только записью.
Тут многое зависит какая школа и если школа не математическая и ребенок в ней, учится не перескакивая через классы, то чаще всего, это 4 класс, а если школа математическая и ребенок минует 4 класс не учась в нем, то тогда, начинают чаще с 3 класса.
Важно учитывать какая школа, да и школьные программы довольно часто меняются, могут быть нюансы.
Но если в целом, то десятичные дроби изучают с 4 класса (точней, проходят) в некоторых школах с 3 класса.
Ну и конечно важно учитывать о какой стране вообще идёт речь.
Понятие десятичной дроби начинают объяснять уже в 3 классе. Понемногу приучают ученика к теме: делят с помощью рисунков и используя спички и полоски бумаги. Полностью десятичные дроби изучаются в 5 классе, когда ребенок будет готов к пониманию определения.
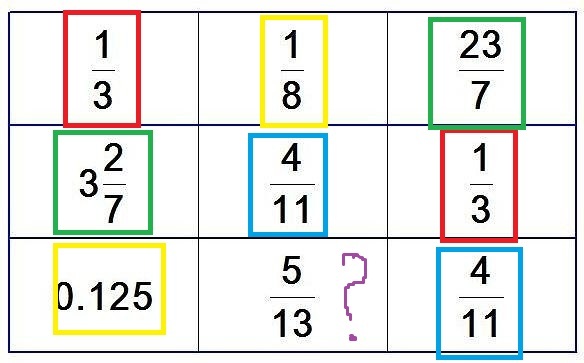
Объясняю: каждое число в таблице имеет свою пару, кроме 5/13
0.125 это десятичная запись дроби 1/8
3 и 2/7 это то же самое, что и 23/7
Остальные числа видны и так, для наглядности предоставлю скрин:
Отвечать на такие вопросы на БВ тяжело, по причине отсутствия шрифтов при помощи которых можно писать дроби. Приходится использовать чужие примеры.
В общем случае умножение и деление дробей происходит по следующему правилу
Несмотря на такую простоту здесь достаточно возможностей для совершения ошибок.
При умножении целого числа на дробь следует помнить что любое целое число должно быть представлено в виде дроби 5/1, 12/1, 48/1 и так далее. Поэтому 1/3 умножают на 4/1 где 1 можно упустить.
Одна целая часть любой дроби равна дроби где числитель и знаменатель равны и имеют значение знаменателя общей дроби.
При использовании отрицательных чисел помним: если в числителе или знаменателе минус то и вся дробь будет с минусом, а если и в числителе и в знаменателе минус то дробь будет с плюсом.
При перемножении дробей в степени их можно преобразовать следующим образом.
Переворот дроби ведет к изменению знака степени.
При умножении двух одинаковых дробей с разными степенями получаем туже дробь в степени являющейся суммой степеней первой и второй дроби.
При сокращении дробей нельзя сокращать члены объединенные между собой знаками плюс и минус. Можно только знаком умножения! Ниже приведено не верное решение.
Повторение курса
1. Десятичная дробь – это форма записи обыкновенной дроби, у которой знаменатель равен 10, 100, 1000 и т.д.
Например, 1/100 = 0,01; 7/10 = 0,7 ; 19/1000 = 0,019
2. Запятая в десятичной дроби отделяет:
— целую часть от дробной;
— столько знаков, сколько нулей в знаменателе обыкновенной дроби.
3. Как перевести десятичную дробь в обыкновенную?
Запишите в числитель все число без запятой, а в знаменатель – единицу и столько нулей, столько цифр было отделено запятой в десятичной дроби.
4. Как обыкновенную дробь перевести в десятичную?
1 способ (хорошо работает, когда в знаменателе дроби: 2, 5, 20, 25… и т. д., то есть когда сразу понятно, на что надо умножать): домножить числитель и знаменатель дроби на такое число, чтобы в знаменателе получилось 10, 100, 1000 и т.д., а потом записать результат в десятичном виде.
2 способ: поделить числитель обыкновенной дроби на ее знаменатель (см. раздел сайта: 5 класс/десятичные дроби).
5. Сложение и вычитание десятичных дробей:
Сложение (вычитание) десятичных дробей выполняется так же, как сложение (вычитание) натуральных чисел, в столбик: главное, чтобы запятая во втором числе стояла под запятой в первом. Например:
6. Умножение десятичных дробей (см. раздел сайта: 5 класс/десятичные дроби/умножение десятичных дробей):
Чтобы перемножить две десятичные дроби, нужно умножить их как обычные числа, не обращая внимания на запятые. Потом сложить количество знаков после запятой в первом множителе и во втором множителе, а затем отделить полученное количество знаков в произведении, считая справа налево. Например:
7. Деление десятичных дробей (см. раздел сайта: 5 класс/десятичные дроби/деление десятичных дробей):
Чтобы разделить десятичную дробь на десятичную дробь, надо перенести запятую в делителе вправо на столько позиций, пока он не станет целым. Потом на столько же позиций перенести запятую в делимом. Затем разделить получившиеся числа как обычно, в столбик. При этом в ответе нужно будет не забыть поставить запятую сразу же, как мы «перейдем за запятую» в делимом. Например:
1. Вычислите:
2. Найдите значение выражения:
3. В летнем лагере за смену в 28 дней израсходовали 1 т картофеля. В первые 12 дней расход картофеля составил 38 кг в день. Каким будет расход картофеля в оставшиеся дни, если каждый день он будет одинаковым?
4. Найдите истинные высказывания. Расположите соответствующие им ответы в порядке возрастания, сопоставив их соответствующим буквам, и расшифруйте астрономический термин. Примеры, в которых допущена ошибка, решите правильно и запишите их в тетрадь.
Н 0,25 + 0,5 = 0,3 Б 0,5 * 3 = 0,15 Т 3,6 : 9 = 0,4
О 3,28 + 1,3 = 4,58 И 4 * 1,7 = 6,8 Я 12,3 : 5 = 24,6
Е=40,4 ; Д=36 ; С=8 ; Н=567 ; У=684,18 ; Л=636 ; Б=728 ; И=872.
7. Соком этого растения был отравлен король датский, отец Гамлета. Сейчас оно входит в состав мазей для лечения простуды, бронхита, плеврита, т. к. вещества, входящие в его состав, оказывают спазмолитическое действие. Что это за растение? (Результат каждого действия даёт букву.)
А=842,4 ; К=844,2 ; Е=23,2; С=93,5 ; Е=9,8 ; О=84,24 ; Н=82,124 ; Б=83,244 ; Л=39,244 ; Я=83,2.
8. Этого симпатичного зверька на латыни именовали «королём зелени». Назовите его:
Б=26 ; О=2,06 ; В=2,6 ; И=66,284 ; А=681,38 ; Л=9,08 ; А=9,8 ; Ц=98 ; Н=229,5 ; Е=0,3203 ; Р=22,95 ; К=32,03 ; К=30.
9. Выполните действия и округлите полученный результат с точностью:
Изучение десятичных дробей в 5 классе
Ищем педагогов в команду «Инфоурок»
ТРУДНОСТИ ПРИ ИЗУЧЕНИИ ДРОБЕЙ
Изучение десятичных дробей начинается и заканчивается в 5 классе. О трудностях, возникающих перед учащимися при изучении дробей, нередко пишут авторы методических пособий. Как правило, изучение обыкновенных дробей дается ученикам 5 класса математики значительно легче десятичных. После изучения сложных тем, ученик просто не понимает к чему учить еще и десятичные дроби. Но как бы там ни было, десятичные дроби необходимы для больших расчетов.
В действующих учебниках в отличие от традиционных не даются формальные определения понятий дроби, обыкновенной и десятичной дробей. Это упрощает изложение теоретического материала, но в то же время усиливает роль задач в правильном понимании и усвоении этих понятий.
Основная цель изучения десятичных дробей в 5 классе – сформировать умение читать, записывать, сравнивать и округлять десятичные дроби, производить четыре арифметических действия над ними. Требования к знаниям и умениям:
— понимать смысл десятичной дроби, как форму записи числа, иметь четкое представление о разрядах дроби;
— уметь читать, записывать, сравнивать, округлять десятичные дроби;
— выполнять сложение, вычитание, умножение, деление десятичных дробей;
Долгие годы в школе изучали обыкновенные дроби до десятичных. К концу 50-х годов математики и методисты сошлись во мнении, что не все благополучно с преподаванием математики в школе. Главную проблему тогда видели в том, что арифметике в школе отводилось слишком много времени в ущерб другим математическим дисциплинам, содержание которых отставало от современных потребностей.
Сложение и вычитание десятичных дробей
Изучение сложения и вычитания десятичных дробей опирается на знание соответствующих действий с целыми числами.
Изучать действия сложения и вычитания целесообразно параллельно, т. е. после каждого случая сложения давать соответствующий по трудности случай вычитания.
Применение наглядных пособий и дидактического материала при изучении арифметических действий с десятичными дробями ограничено. Средством наглядности служит сама запись арифметических примеров, особенно запись в столбик.
Итак, прежде чем знакомить учащихся со сложением и вычитанием десятичных дробей, необходимо повторить сложение и вычитание целых чисел и обыкновенных дробей.
Ошибки в выполнении действия чаще всего наблюдаются, когда нужно „занимать” единицу высшего разряда (производить раздробление, например, одной десятой в сотые). Ученики должны понять, что сложение десятичных дробей выполняется по разрядам так
же, как и натуральных чисел. При этом необходимо следить, когда происходит перенос единицы в следующий разряд. Аналогично вводится и действие вычитания. Чтобы учащиеся лучше уяснили его смысл, надо предлагать проверять правильность вычитания сложением, требуя обоснования.
Умножение и деление десятичных дробей
ПРАВИЛО: Чтобы умножить одну десятичную дробь на другую, надо выполнить умножение, не обращая внимания на запятые, а затем в результате отделить справа запятой столько цифр, сколько их стоит после запятой в обоих множителях вместе.
Наибольшие трудности для учащихся представляют примеры, в которых в первом множителе один или несколько десятичных раков равны нулю, а также примеры, в которых в произведении случается нуль целых.
Прежде чем переходить к делению десятичной дроби на десятичную дробь, с учащимися следует выполнить задания на закрепление правила деления десятичной дроби на натуральное число, которое ляжет в основу деления на десятичную дробь.
Основными причинами низкого качества усвоения понятия дроби (а также и последующих затруднений, с которыми сталкиваются учащиеся при его изучении) заключаются в механическом заучивании, в недостаточном внимании к осознанному восприятию понятия, установлению взаимосвязи между множествами изученных и вновь введенных чисел, выявлению общих и особенных характеристик этих множеств.
Не секрет, что у детей с прочными вычислительными навыками гораздо меньше проблем с математикой.
Вычислительные навыки достигают высшего уровня своего развития лишь в результате длительного процесса целенаправленного их формирования. Формирование у школьников вычислительных навыков остаётся одной из главных задач обучения математике, поскольку вычислительные навыки необходимы при изучении арифметических действий.
Уверенное представление о дроби возникает только тогда, когда учащийся самостоятельно проходит все ступени по формированию этого понятия, то есть при изучении дробей необходим творческий метод обучения.