в каком классе изучается факториал
Класс: 5
Презентация к уроку
Тип урока – изучение нового материала с элементами закрепления.
Оборудование – презентация к уроку.
Этапы урока
Деятельность учителя
Деятельность учащихся
Быль: «Однажды на экзамене…»
Преподаватель: Прочитайте выражение:
Студент: Единица, деленная на два-а-а. Плюс единица, деленная на три-и-и. Плюс единица, деленная на четы-ы-ыре.
Преподаватель: Постойте, постойте…Почему вы кричите?
Студент: Но там же написаны восклицательные знаки.
Давайте узнаем, что обозначает символ восклицательного знака в математике.
Факториалом числа n называется произведение всех натуральных чисел от 1 до n:
(n! читается: «эн факториал»).
Записывают определение в тетрадь.
,
,
.
3. Приведи к несократимому виду дроби:
,
,
,
,
,
.
4. Приведи дроби к наименьшему общему знаменателю:
,
,
,
.
5. Найди значение разностей:
,
,
,
.
Запиши следующие две разности и найди их значение. Чему равна разность 
Решают примеры, опираясь на введенное определение.
с использованием факториала числа.
Использованная литература:
Дорофеев Г. В., Петерсон Л. Г. Математика. 5 класс. Часть 2.- М.: Издательство «Ювента», 2007.
Презентация по математике на тему «Факториал»(5 класс)
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
ЦЕЛЬ : решать задачи из раздела «Комбинаторика». Объект исследования: раздел математики – «Комбинаторика».
задачи исследования: 1) определить одну из областей применения формул комбинаторики; 2) провести перебор вариантов ; 3) посмотреть методы решения задач комбинаторики.
Комбинаторика – раздел математики, в котором изучают вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям можно составить из данных объёктов. Выбором объектов и расположением их в том или ином порядке приходиться заниматься чуть ли не во всех областях человеческой деятельности. Комбинаторика нужна для изучения раздела математики «Теория вероятностей», который будет являться обязательным при изучении школьного курса математики.
С аналогичными задачами, получившими название комбинаторных, люди столкнулись в глубокой древности. В Китае увлекались составлением магических квадратов, в Древней Греции подсчитывали число различных комбинаций длинных и коротких слогов стихотворных размеров. Комбинаторные задачи возникли в связи с такими играми, как шашки, шахматы, карты, кости и др. Чтобы их решить, нужно было уметь подсчитывать число различных комбинаций, подчинённых тем или иным условиям.
С помощью таблицы 12 вариантов! Плюшка Бутерброд Пряник Кекс Кофе Сок Кефир
Дерево возможных вариантов * БББ, ББК, БКБ, КБК, ККБ, ККК
В данных примерах был осуществлен способ перебора возможных вариантов (возможных комбинаций). Решения данных задач основывается на общем правиле умножения.
«Правило умножения» Для того чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В
С помощью графов По окончанию деловой встречи 4 специалиста обменялись визитными карточками (каждый вручил свою карточку каждому). Сколько визитных карточек было роздано? Решение. Ответ. 12 визиток 1 2 4 3 1
Посчитаем число перестановок для 4 элементов: 1234, 1243, 1324, 1342, 1423, 1432, 2134, 2143, 2314, 2341, 2413, 2431, 3124, 3142, 3214, 3241, 3412, 3421, 4123, 4132, 4213, 4231, 4312, 4321.
Для числа перестановок n элементов есть обозначение: n! Например, 4! = 1 · 2 · 3 · 4= 24
Свойство факториала (n + 1)! = (n + 1) * n!. п = 3, (3 + 1)!=(3 + 1) * 3!
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДБ-179092
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Роспотребнадзор продлил действие санитарных правил для школ
Время чтения: 1 минута
В школе в Пермском крае произошла стрельба
Время чтения: 1 минута
В Тюменской области студенты и школьники перейдут на дистанционное обучение
Время чтения: 2 минуты
В Приамурье начнут пускать на занятия только привитых студентов
Время чтения: 0 минут
Школьники Свердловской области с 8 ноября перейдут на дистанционку
Время чтения: 0 минут
В Туве предложили ввести антиковидные паспорта для школьников
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Факториал
Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Формулы и свойства факториала
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
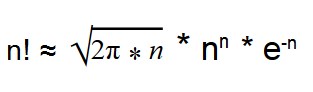 |
Рекуррентная формула
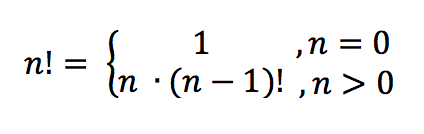 |
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
 ray_binko
ray_binko
Без году 40 или три по тринадцать
Армию из тысячи человек собрать легко, трудно найти генерала
Вообще-то эта история еще на прошлой неделе случилась, но явно не устарела, поэтому сегодня перескажу. Очередная история из серии «Учимся мы с сыном в 5-м классе».
Прихожу вечером домой с работы и собираюсь традиционно у сына уроки проверять. И тут выясняется, что в домашнем задании по математике у него есть задача, которую не может решить никто. Ни он, ни мама, ни бабушка, ни дедушка… У меня глаза, понятно, загорелись – сейчас папа даст мастер-класс решения нерешаемых школьных задач и повысит свой рейтинг в глазах сына пунктов на 150.
Папа берет учебник математики за 5-й класс и читает задачу № 807: «Аня, Даша, Лена, Марина и Женя пришли к зубному врачу. Сколькими способами они могут встать в очередь?». Уп-с.
Папа помнит, что на третьем курсе универа на «Теории Вероятности» его учили решать такие задачи через факториалы. И это называется то ли «число сочетаний», то ли «число размещений» и решается как-то очень просто – факториал от пяти, что-ли…
Но папа понимает, что это задача взята из учебника для 5-го класса, где факториалов вроде как не должно быть в принципе. Значит, должно быть, какое-то другое решение – простое и понятное пятикласснику. Но все попытки найти это решение к результату не приводят. 5 девочек, 5 мест в очереди – но не 5 х 5 = 25, же, правда?
Папа начинает листать учебник, чтобы понять какую вообще дети проходят тему, что к ней такие задачи дают. Тема называется «Степени числа: квадрат, куб». Причём тут девочки в очереди и степени числа непонятно в принципе. Папа открывает ответы в конце учебника, но там нет ответа именно на эту задачу!
Папа лезет в Интернет в надежде найти какой-нибудь сайт, посвященный решениям задач по математике для пятиклассников. Зря смеетесь – папа находит и скачивает PDF-файл с ответами к задачам вроде бы этого учебника (по крайней мере, двое из четырех авторов совпадают), но выясняется, что учебник всё же другой и ответ на задачу 807 не имеет ничего общего с девочками и зубными врачами.
Папа впадает в прострацию. Но тут является счастливый сын и объявляет, что он, кажется, перепутал (!?) – им задали задачу № 801, а он написал «1» похожую на «7» (!!), вот и вышло № 807. 801-я задача, к счастью, действительно связана с квадратами и кубами, и папа с сыном легко и быстро её решают.
Но неприятный осадок, то остался! На следующее утро папа обращается к знакомым математикам и те объясняют, что это реально задача на факториалы, это действительно число сочетаний, которое считается как 5! (факториал пяти) и равно 5*4*3*2*1=120. Других вариантов решения этой задачи – для пятого класса – математики предложить не могут.
Или факториалы сейчас это реально тема пятого класса? Нет, понятно, что папа учился в школе еще при Царе Горохе, но неужели умственная акселерация нового поколения зашла так далеко? Мне всегда казалось, что там в другую сторону всё движется.
И снова не могу не процитировать Пушкина: «О сколько нам открытий чудных готовит просвещенья дух…». И это только пятый класс, ребята…
Что такое факториал?
Я думаю трудно найти человека, который не знал бы, что такое факториал. Но, чёрт возьми, такая красивая математическая операция, давайте поговорим о ней снова. Тем более постарался максимально доходчиво объяснить материал даже очень далеким от математики людям. Поехали!
Кто из Вас помнит, когда столкнулся с факториалом впервые? Я, например, абсолютно уверен, что первый раз увидел значок n! на советской микро-ЭВМ Электроника МК-71. Меня поразило, в первую очередь, как с помощью этой кнопки быстро переполняется буфер и выскакивает ошибка. Потом уже, начав изучать математику, удалось поближе познакомиться с этим зверем. Начнем с определения:
Лаконично и просто.
Факториал крут тем, насколько быстро возрастает его значение, и если 5! равен всего лишь 120, то 10! — уже 3 628 800, а, например, факториал 1000000 равен 8,263931688Е+5565708. Факториал возрастает быстрее чем экспонента и степенная функция и даже чем их произведение, но, однако уступает функции n в степени n.
Короткий пример вычисления факториала
Важное уточнение: 0! = 1, что следует из определения факториала.
Если взять первым красный шар, а затем найти варианты расположения остальных — получим 6 вариантов. Перебрав все 4 шара получим 24 = 1*2*3*4=4! Таким образом, количество перестановок во множестве равно факториалу количества его членов.
Во-вторых, факториал применяется при расчете количества размещений — еще одной операции из мира комбинаторики. Суть ее проста, поясним ее на всё том же примере разноцветных шаров. Ответьте на вопрос: сколько способов отдельного размещения 2 шаров из представленных 4 (разный порядок — разный способ) ?
Всего имеется 12 вариантов размещения 2 элементов из 4. То, что мы сейчас посчитали руками формализуется следующим образом через факториал:
Читается как количество размещений из n элементов по m
В-третьих, факториал присутствует в формуле количества сочетаний из n элементов по m. Сочетания отличаются от размещений тем, что если набор элементов одинаков — он не учитывается.
На рисунке обведены сочетания: как видно, их стало в 2 раза меньше. Формула вычисления количества сочетаний из n элементов по k выглядит так:
Раз уж мы разобрались с перестановками, размещениями и сочетаниями, перейдем к «имени нарицательному», страшному и пугающему: биному Ньютона. Как окажется, знание факториала и последней формулы легко позволит Вам расколоть этот «крепкий орешек».
Как ни странно, бином Ньютона это выражение (1+x)^n и его легко найти через формулу сочетаний (доказательство естественно опустим). Вот небольшой пример нахождения бинома третьей степени, который легко перепроверить перемножением.
Разобравшись с этим примером, можете спокойно спорить с друзьями и знакомыми, что без проблем вычислите бином Ньютона n-ной степени!
Некоторые интересные свойства факториала
Во многих случаев, когда не требуется точного вычисления факториала не требуется, можно воспользоваться формулой Стирлинга:
Например, реальное значение факториала 5 — это 120. По формуле Стирлинга получается так:
Строго говоря, это только первый член бесконечного ряда. С увеличением количества членом приближение будет всё точнее
Идем дальше. До этого мы условились, что в качестве подфакториальной переменной, рассматриваем только натуральные числа. А что, если бы нам захотелось вычислить факториал дробного числа? Оказывается, и такой факториал тоже существует.
Используются такие расчеты при статистическом описании нейронных сетей. Данные вычисления приближенные, чтобы точно вычислять значение таких факториалов, используется Гамма-функция. Но это уже совсем другая история.
Есть еще двойной факториал, обозначаемый n!!. Формула его вычисления зависит от четности или нечетности аргумента.
Думаю принцип понятен без дополнительных пояснений.
Кроме того, существует «король факториалов», так называемый суперфакториал, который равен произведению факториалов числа, меньше либо равного данному:
Ну а дальше пошло-поехало: придумали гиперфакториалы, которые равны произведениям суперфакториалов, а потом и вовсе обобщили в m-кратный факториал.
Вот еще несколько интересных свойств факториала и заканчиваем:
1) n! — никогда не является квадратом какого-либо числа.

 ,
,  ,
,  .
. ,
,  ,
,  ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
.





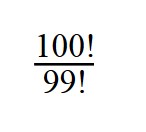
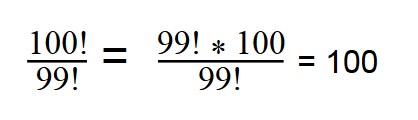
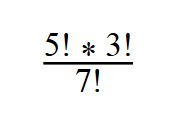
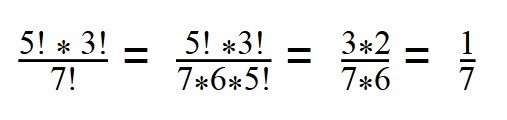
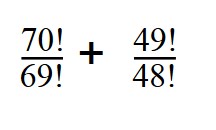
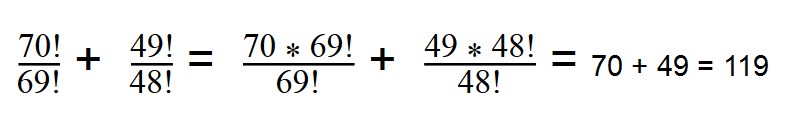
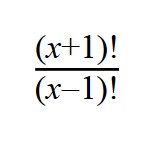
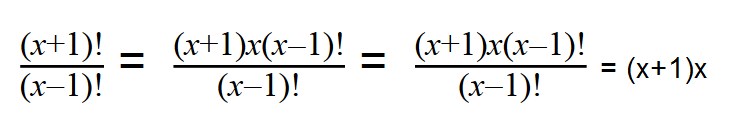


 ray_binko
ray_binko