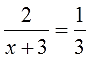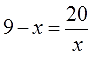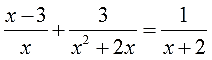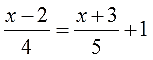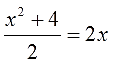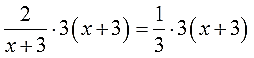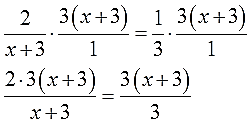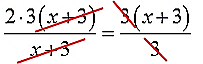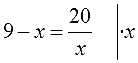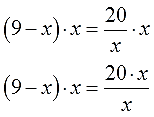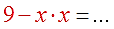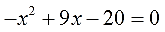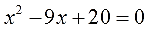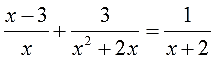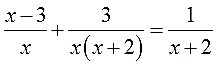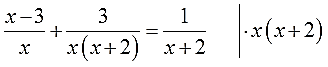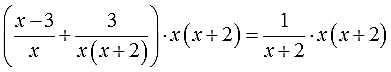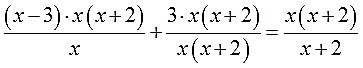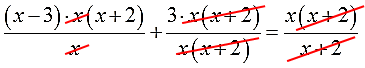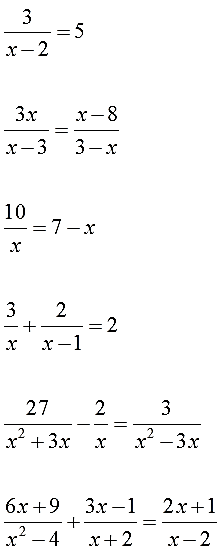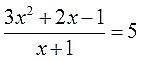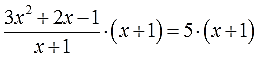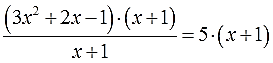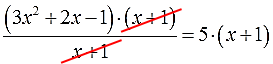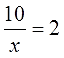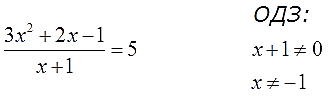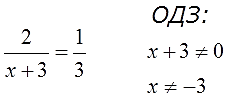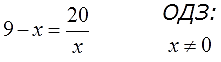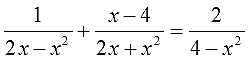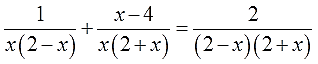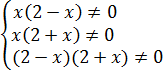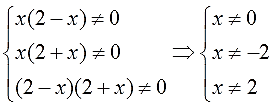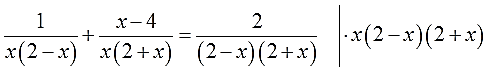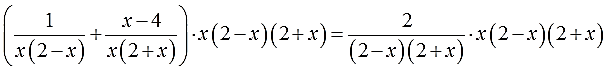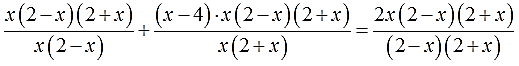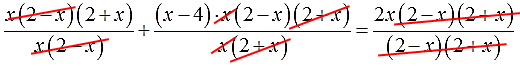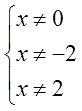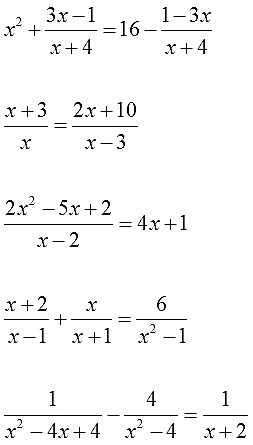Как убрать дробь в уравнении
Как решать уравнения с дробями. Показательное решение уравнений с дробями.
Решение уравнений с дробями рассмотрим на примерах. Примеры простые и показательные. С их помощью вы наиболее понятным образом сможете усвоить, как решать уравнения с дробями.
Например, требуется решить простое уравнение x/b + c = d.
Уравнения такого типа называется линейным, т.к. в знаменателе находятся только числа.
Решение выполняется путем умножения обоих частей уравнения на b, тогда уравнение принимает вид x = b*(d – c), т.е. знаменатель дроби в левой части сокращается.
Например, как решить дробное уравнение:
x/5+4=9
Умножаем обе части на 5. Получаем:
х+20=45
x=45-20=25
Другой пример, когда неизвестное находится в знаменателе:
Уравнения такого типа называются дробно-рациональными или просто дробными.
Решать дробное уравнение бы будем путем избавления от дробей, после чего это уравнение, чаще всего, превращается в линейное или квадратное, которое решается обычным способом. Следует только учесть следующие моменты:
Здесь вступает в силу такое понятие, как область допустимых значений (ОДЗ) – это такие значения корней уравнения, при которых уравнение имеет смысл.
Таким образом решая уравнение, необходимо найти корни, после чего проверить их на соответствие ОДЗ. Те корни, которые не соответствуют нашей ОДЗ, из ответа исключаются.
Например, требуется решить дробное уравнение:
Исходя из вышеуказанного правила х не может быть = 0, т.е. ОДЗ в данном случае: х – любое значение, отличное от нуля.
Избавляемся от знаменателя путем умножения всех членов уравнения на х
И решаем обычное уравнение
5x – 2х = 1
3x = 1
х = 1/3
Решим уравнение посложнее:
Здесь также присутствует ОДЗ: х -2.
Решая это уравнение, мы не станем переносить все в одну сторону и приводить дроби к общему знаменателю. Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.
Это самое обычное умножение дробей, которое мы уже рассмотрели выше
Запишем это же уравнение, но несколько по-другому
Левая часть сокращается на (х+2), а правая на 2. После сокращения получаем обычное линейное уравнение:
х = 4 – 2 = 2, что соответствует нашей ОДЗ
Для закрепления материала рекомендуем еще посмотреть видео.
Решение уравнений с дробями не так сложно, как может показаться. В этой статье мы на примерах это показали. Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в комментариях.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Как решить уравнение с неизвестным в дроби
Иногда линейные уравнения принимают вид, когда неизвестное оказывается в числителе одной или нескольких дробей. Как, например, в уравнении ниже.
В таких случаях подобные уравнения можно решить двумя способами.
I способ решения
Сведение уравнения к пропорции
При решении уравнений способом пропорции необходимо выполнить следующие действия:
Итак, вернемся к нашему уравнению. В левой части у нас и так стоит только одна дробь, поэтому в ней не нужны никакие преобразования.
Будем работать с правой частью уравнения. Упростим правую часть уравнения так, чтобы там осталась только одна дробь. Для этого вспомним правила сложения числа с алгебраической дробью.
Теперь используем правило пропорции и решим уравнение до конца.
II способ решения
Сведение к линейному уравнению без дробей
Рассмотрим уравнение выше еще раз и решим его другим способом.

| x − 4 |
| 5 |
» и «
| 2x + 4 |
| 9 |
».
Наша задача сделать так, чтобы в уравнении не осталось ни одной дроби.
Другими словами, необходимо свести уравнение к обычному линейному уравнению без неизвестного в дроби.
Чтобы избавиться от дробей в уравнении нужно:
Умножим каждый член уравнения на « 45 ».
При умножении уравнения на число нужно каждый член уравнения умножить на это число.
Как решать дробные уравнения?
Итак, друзья, продолжаем осваивать решение основных типов алгебраических уравнений. Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений — дробными уравнениями.
Дробные уравнения — незаменимая вещь во многих других темах математики. Особенно — в текстовых задачах. Но для успешного их решения жизненно необходимо ориентироваться в трёх смежных темах:
1. Дроби и действия с дробями и дробными выражениями.
3. Решение линейных и квадратных уравнений.
Без этих трёх китов браться за решение дробных уравнений слишком уж самонадеянно, я бы сказал. Почему? Да потому, что непонимание, как, скажем, работать с дробями (сокращать, приводить к общему знаменателю и т.д.) автоматически будет приводить к полному провалу и в дробных уравнениях. Намёк понятен?)
Так что тем, у кого проблемы хотя бы по одной из вышеперечисленных тем — настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись.
Что такое дробное уравнение? Примеры.
Например, вот такое уравнение:
И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относятся. Либо это линейные уравнения, либо квадратные.
Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что знаменатели дробей — четвёрка и пятёрка. Т.е. просто числа. И ни один из знаменателей не содержит иксов.
Или такое уравнение:
Это обычное квадратное уравнение, несмотря на двойку в знаменателе. Опять же, по причине того, что двойка — не икс, и деления на неизвестное в дроби нету.
Как решать дробные уравнения? Убираем дроби!
Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. По чётким и несложным правилам. Каким же именно образом?
Первым делом надо избавиться от дробей! Это ключевой шаг в решении любого дробного уравнения, который должен быть освоен идеально. Ибо после того, как все дроби исчезли, уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы уже с вами знаем, что делать.)
Но… Как же нам избавиться от дробей?! Легко! Применяя всё те же старые добрые тождественные преобразования! В чём же суть?
Вникаем. Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее.)
Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:
Первое, что приходит на ум — перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как кошмарный сон! Так делают только в одном случае — при решении дробно-рациональных неравенств методом интервалов. Это отдельная большая тема.
А в уравнениях нам надо сразу умножить обе части на такое выражение, которое нам позволит сократить все знаменатели. И какое же это выражение?
Давайте его конструировать.) Смотрим ещё раз на уравнение:
Понятно, что в левой части для ликвидации знаменателя нам необходимо умножение на (х+3), а в правой — на 3. Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные — не катит. Ничего не поделать, так уж она устроена…)
Значит, нам надо скомбинировать такое выражение, которое одновременно делилось бы как на (х+3), так и на тройку. Причём очень важно — только с помощью умножения! И какое же это выражение? Очевидно, это 3(х+3). То есть, по сути, общий знаменатель обеих дробей.
Итак, для ликвидации всех дробей наше уравнение надо умножать на выражение 3(х+3).
Это самое обычное умножение дробных выражений, но, так уж и быть, расписываю детально:
Прошу обратить внимание: скобки (х+3) я не раскрываю! Прямо так, целиком, их и пишу, как будто бы это одна буква. Ибо наша основная на данный момент задача — дроби убрать. Чего без произведения никак не сделаешь… И зачем же нам тогда париться с раскрытием скобок?!
А вот теперь мы видим, что в левой части сокращается целиком (х+3), а в правой 3. Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:
Вот и отлично. Дроби исчезли. После сокращения получилось безобидное линейное уравнение:
А его (надеюсь) уже решит каждый:
Решаем следующий примерчик:
И опять избавляемся от того, что нам не нравится. В данном примере это дробь 20/х. Одна единственная. Для её ликвидации правую часть надо домножить на знаменатель. То есть, просто на х. Но тогда и левую часть тоже надо домножить на х: так уж второе тождественное преобразование требует.
Вот и домножаем! Всю левую часть и всю правую часть:
Напоминаю, что эта вертикальная чёрточка с умножением всего лишь означает, что обе части нашего уравнения мы умножаем на «х».
А вот теперь — снова внимание! Очередные грабли. Заметьте, что при умножении левой части на икс, выражение (9 — х) я взял в скобки! Почему? Потому, что мы умножаем на икс всю левую часть целиком, а не отдельные её кусочки!
Дело всё в том, что частенько после умножения народ записывает левую часть вот так:
Это категорически неверно. Дальше можно уже не решать, да…)
Но у нас всё хорошо, будем дорешивать.
С чистой совестью сокращаем икс справа и получаем уравнение уже безо всяких дробей, в одну строчку.
Вот и отлично. Все дроби исчезли напрочь, теперь можно и скобки раскрыть:
Переносим всё влево и приводим к стандартному виду:
Получили классическое квадратное уравнение. Но минус перед квадратом икса — нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнения на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:
Решаем через дискриминант (или подбираем по теореме Виета) и получаем два корня:
Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь — квадратным.
А бывает и так, что после ликвидации дробей вообще все иксы сокращаются и остаётся чистая правда. Что-нибудь типа 3=3. Это означает, что икс может быть любым. Какой икс ни возьми — всё равно всё посокращается и останется железное равенство 3=3.
Или наоборот, может получиться какая-нибудь белиберда, типа 3=4. А это будет означать, что корней нет. Какой икс ни возьми — всё сократится и останется бред…
Надеюсь, такие сюрпризы вас уже нисколько не удивят.) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее — особые случаи при решении линейных уравнений. Эти сюрпризы (полная пропажа иксов после преобразований) — они ко всем видам уравнений относятся. И дробные — не исключение.)
Разумеется, при попытке ликвидации дробей встречаются и неожиданности. И одну из них мы рассмотрим прямо сейчас.
Раскладываем на множители!
Решаем третье уравнение по списку:
А вот тут некоторые могут и зависнуть. На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить
и домножить на эту конструкцию всё уравнение. Математика не возражает.) Но… Может быть, есть выражение попроще?
Что ж, вскрою тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители. Привет седьмому классу!)
А попробуем-ка разложить на множители каждый из знаменателей? Ну, с х и х+2 точно ничего не сделать, а вот х 2 +2х вполне себе раскладывается! Выносим один икс за скобку и получаем:
Отлично. Вставим наше разложение в исходное уравнение:
Вот теперь всё и прояснилось.) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х(х+2). Это выражение гораздо короче и прекрасно делится на каждый из знаменателей: и на x, и на (х+2), и само на себя — на х(х+2).
Вот на х(х+2) и умножаем:
И снова расписываю подробно, дабы не запутаться. В левой части я буду использовать скобки: там сумма дробей. В правой части скобки не нужны: там одна дробь. Вот и пишем:
А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем — вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:
Я уж не стал здесь рисовать единички в знаменателях, несолидно… И, опять же, малые скобки в числителях я не раскрываю! Они нам сейчас для сокращения понадобятся! И да… Откуда появились скобки (х — 3) в числителе первой дроби — думаю, уже не стоит объяснять?)
С удовольствием сокращаем все дроби:
Раскрываем оставшиеся скобки, приводим подобные и собираем всё слева:
И снова получили квадратное уравнение.) Решаем и получаем два корня:
Вот и всё. Это и есть ответ.)
Из этого примера можно сделать важный вывод:
Если знаменатели дробей можно разложить на простые множители — обязательно делаем это! Пригодится при ликвидации дробей. Причём раскладываем всё до упора, используя все возможные способы из алгебры седьмого класса!
Как вы видите, всё просто и логично. Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это — дроби. И точно так же мы будем поступать и со всякими логарифмами, синусами, показателями и прочей жестью.) Мы всегда будем от всего этого избавляться.)
Ответы (как обычно, вразброс):
Последнее задание не решается? Что ж, формулы сокращённого умножения всяко помнить надо, да…)
Всё решилось? Что ж, здорово! Значит, полпути в решении дробных уравнений мы с вами уже преодолели. Эта первая часть пути — избавление от дробей. Осталась вторая. Не менее важная!
Всё просто, но… Пришло время открыть вам горькую правду. Успешное решение дробных уравнений этого урока вовсе не гарантирует успех в решении всех остальных примеров этой темы. Даже очень простых, подобных этим. К сожалению…
ОДЗ в дробных уравнениях
В предыдущем уроке мы с вами освоили основной принцип решения любых дробных уравнений. Это — ликвидация дробей. Кто читал, тот понял, что ничего сложного в этом нет.
Однако, даже в самых простых (казалось бы!) дробных уравнениях нас может поджидать сюрприз не из приятных. С ним, с сюрпризом, надо разобраться! Разберёмся?)
Основная проблема в решении дробных уравнений.
Сейчас мы с вами научимся обходить одну из самых коварных ловушек на ЕГЭ и контрольных! Попадаются в неё все — и троечники и отличники. Я специально поставил её в самое примитивное уравнение, чтобы с ней (с ловушкой) хорошенько разобраться. Но для начала посмотрим, попадёте вы в неё или нет.)
Допустим, надо решить вот такое нехитрое уравнение:
Дело уже привычное и знакомое. Умножаем всё уравнение на знаменатель (х+1) и получаем:
Напоминаю, что со скобками (х+1) работаем целиком, как будто бы это одно число! Производим умножение:
Сокращаем знаменатель и избавляемся от дроби:
Раскрываем оставшиеся скобки, переносим всё влево, приводим подобные:
Делим всё уравнение на 3 и получаем:
Отлично. Самое обычное квадратное уравнение. Решаем и получаем два корня:
Предположим, в задании на ЕГЭ сказано записать в ответ меньший из корней, если корней более одного. Что писать будем?)
Так в чём же дело? А вы попробуйте проверку сделать. Подставьте каждый из найденных иксов в исходное уравнение. И, если при х=2 у вас всё славненько срастётся, получится тождество 5=5, то при х=-1 получится деление на ноль! Чего делать нельзя категорически. Нет такой операции ни в природе, ни в математике…
Что это значит? Это значит, что х=-1 — так называемый посторонний корень. Или лишний корень. Он не является корнем нашего дробного уравнения и в ответе никак не учитывается. Ибо его подстановка даёт бессмыслицу. Его мы просто отбрасываем. Окончательный корень один.
Так, стоп, что-то тут не так! Нам же говорили, что всё уравнение можно умножать на одно и то же выражение! Это же тождественное преобразование!
Да, тождественное. Я не спорю. Но при одном маленьком ограничении, которое многие попросту игнорируют. А именно — выражение, на которое умножаем (делим), отлично от нуля! А скобочка (х+1) при х=-1 обращается в ноль! Так что всё честно.
И что нам теперь делать? Совсем не умножать? Тогда мы вообще ничего не решим! Каждый раз проверку делать? Это с ума сойдёшь. Особенно, если уравнение навороченное.
Нет, мы с вами пойдём красивым и элегантным путём. Обратимся за помощью к трём волшебным буквам! Догадались? Да! Это ОДЗ! Область Допустимых Значений.
Что же такое ОДЗ?
Это такие значения икса, которые могут быть в принципе. Или которые разрешены для данного примера.
Например, в уравнении
мы ещё пока не знаем, чему равен икс, верно? Мы уравнение пока не решили. Но зато мы железно знаем, что икс не может равняться нулю ни в коем случае! На ноль делить нельзя. На любое другое число — целое, дробное, отрицательное, иррациональное — ради бога. А вот на ноль — никак. Стало быть, в этом примере ОДЗ:
х — любое число, кроме нуля.
Как записывать ОДЗ? Как работать с ОДЗ?
Тоже легко. На первом этапе всегда внимательно осматриваем исходный пример и ищем опасные места. Что значит опасные места?
Это места, где возможны запретные действия. Действия, которые при каких-то иксах могут оказаться недопустимыми с точки зрения математики. В нашей теме такое действие всего одно — деление. Нельзя делить на ноль. Есть ещё запреты в корнях чётной степени, в логарифмах и в тригонометрии. Их мы тоже рассмотрим в соответствующих уроках.
Как только опасные места найдены, рядышком с примером выписываем условия, которые не приводят к бессмыслице. После этого, глядя на эти условия, вычисляем запретные иксы. И исключаем их из ОДЗ. Вот и всё.
Я специально акцентирую внимание на словах «исходный пример». Любое преобразование (сокращение, приведение подобных и т.п.) может изменить ОДЗ, и мы можем получить неверный ответ.
Важно! Для поиска ОДЗ мы не решаем пример! Мы решаем всего лишь маленькие кусочки примера для нахождения запретных иксов.
«Многа букаффф», да. Но на практике вся процедура выглядит до ужаса элементарно.
Итак, берём наше уравнение:
Ничего пока что не трогаем, а внимательно осматриваем исходное уравнение. Осмотрев, мы сразу замечаем операцию деления на х+1.
Это потенциально опасная операция: при каких-то значениях икса выражение х+1 может оказаться равным нулю. На который делить нельзя. Поэтому обезопасим себя вот такой записью:
х+1 ≠ 0
Во-о-т. Минус один категорически не подходит нам в качестве ответа. Это и будет ОДЗ для нашего уравнения. Все иксы, кроме минус единички.
На практике запись и нахождение ОДЗ обычно оформляют так:
Иногда ОДЗ записывают и в другой форме, через промежутки. Вот так:
Читается эта запись так: «Икс принадлежит интервалу от минус бесконечности до минус единицы (не включая), и от минус единицы (не включая) до плюс бесконечности.»
Перевод с математического на человеческий: «Икс — любое число, кроме минус единицы.»
Вот и всё. Как только мы себя обезопасили такой записью, дальше мы имеем полное право делать с уравнением всё что хотим — переносить члены, домножать, сокращать… Вот и домножаем всё уравнение на (х+1). Дробь-то убирать всё равно надо! Это по-прежнему будет не совсем тождественным преобразованием, но все вредные последствия от нарушения тождественности мы исключим по ОДЗ.
Как вы думаете, в какой же момент мы с вами попали в ловушку элементарного примера? Как раз в момент домножения всего уравнения на знаменатель дроби! Знаменатель исчез, и вместе с ним исчезли и соответствующие ограничения на иксы. Бесследно. И для нового уравнения, без дроби, на икс уже не накладывается никаких запретов! Любым может быть икс…
В математике это явление называется расширение ОДЗ.
Но теперь мы уже с вами народ бдительный. Исходные ограничения (х≠-1) мы записали и сохранили.
Поэтому дальше спокойно решаем уравнение безо всяких дробей и получаем два корня:
А вот теперь стыкуем наши результаты и условия ОДЗ. И видим в наших кандидатах на ответ один из иксов в качестве запретного! Минус один. Это означает, что в окончательный ответ его включать нельзя. Это посторонний корень, появившийся в процессе решения без нашего желания.
Да, это законный корень нашего вспомогательного квадратного уравнения, но никак не корень исходного дробного уравнения!
Стало быть, минус единицу мы безжалостно вычёркиваем и в ответ не включаем. Вот и всё.)
А в других уравнениях прошлого урока? Там что, нет ОДЗ? Есть, разумеется. Есть деление на икс — есть и ОДЗ.
В первом уравнении:
Во втором уравнении:
Я специально в тех примерах ничего не сказал про ОДЗ. Чтобы вас не перегрузить раньше времени.) В всех уравнениях прошлого урока (и домашнего задания к нему) ОДЗ никак не сказывалась на ответе. Так бывает. Но в заданиях ОГЭ и ЕГЭ ОДЗ в 99% случаев влияет на ответ! Так что мы с ОДЗ дружить будем. И во всех темах, где это необходимо, мы будем про ОДЗ вспоминать. Чтобы не упасть лицом в грязь.)
Итак, про ОДЗ поговорили. Убедились, что работать с ней тоже совсем не сложно. Теперь можно перейти и к общему алгоритму решения любого дробного уравнения.
Решаем дробные уравнения по алгоритму!
Для успешного решения любого дробного уравнения необходимо выполнить (правильно) пять пунктов:
1. Разложить знаменатели всех дробей на множители (если требуется). До упора. Переписать уравнение с учётом этого факта.
2. Найти ОДЗ, записать рядышком с уравнением и временно (до конца решения) забыть про неё.
3. Сообразить, на что надо умножить обе части уравнения, чтобы все дроби исчезли полностью.
4. Выполнить это самое умножение и решить новое уравнение, уже безо всяких дробей. Найти решения (кандидаты в ответ).
5. Вспомнить про ОДЗ и состыковать найденные решения с условиями ОДЗ. Те решения, которые не входят в ОДЗ, безжалостно выбросить. Записать окончательный ответ.
А теперь, вооружившись таким мощным супероружием, как ОДЗ, и общим алгоритмом, разберём очередной пример. Супердетально разберём!
Решаем строго по пунктам. Выполняем пункт первый:
1. Разложить все знаменатели на множители (если требуется). До упора. Переписать пример с учётом этого факта.
Знаменатели наших дробей НЕ разложены на множители. Вот и приступаем. Вынесение общего множителя за скобки и формула разности квадратов — мощные штуки.)
Вот так. А теперь переписываем уравнение с учётом наших разложений:
Готово. Все знаменатели разложены до упора.) Можно приступать ко второму пункту.
2. Найти ОДЗ, записать рядышком с примером и временно (до конца решения) забыть про неё.
Итак, начинаем осматривать исходный пример на наличие опасных операций.
Внимание! Ничего не трогаем и не решаем! Не складываем дроби, не приводим подобные, не сокращаем.
Подобные преобразования запросто могут изменить ОДЗ, что может привести к неверному ответу! Оно нам надо?! Ещё раз напоминаю: ДО поиска ОДЗ с исходным примером мы не делаем НИЧЕГО! Кроме разложения на множители. Оно — безопасно и даже полезно.)
Берём и именно осматриваем исходный пример. И замечаем три опасных места: каждая из дробей таит в себе возможное деление на ноль.
Знак системы (фигурная скобка) здесь не зря поставлен. Она означает, что все три условия должны выполняться одновременно! Мы ведь ОДЗ записываем не для каждой дроби по отдельности, а для всего примера целиком.)
Ну и как? Нашли ОДЗ? Не-а…)
Мы записали кусочек примера, записали три требования, которые должны выполняться железно. Но этого мало. Нужно ещё найти иксы, которые обеспечивают эти железные требования. ОДЗ ведь к иксам относится, а не к кусочкам примера…
Как же найти значения иксов, которые не превращают знаменатели дробей в ноль? Их же очень много? Очень просто! Мы поступим элегантно. Найдём иксы, которые наоборот, превращают знаменатели дробей в ноль. Это и будут запретные иксы.
Вот и решаем эти неравенства методом «от противного». То есть, делаем из неравенств уравнения:
Именно из этих трёх уравнений мы и будем искать запретные иксы. Уравнения очень простые: произведение равно нулю, когда хотя бы один из множителей равен нулю. Вот и приравниваем (в уме или на черновике) каждый множитель к нулю.
Вспомнив, что это запретные иксы, получим:
х ≠ 0; x ≠ 2.
Точно так же решаем и два оставшихся уравнения.
Для второго уравнения получаем:
И, наконец, для третьего уравнения получаем:
Видно, что некоторые запретные значения иксов повторяются. Разумеется, для окончательной записи ОДЗ мы их не будем дублировать. Итого ОДЗ для нашего уравнения будет выглядеть вот так:
Видите, насколько полезно предварительно раскладывать знаменатели на множители! В уме ОДЗ ищется! Поэтому эта процедура и стоит первым пунктом в алгоритме.)
Можно приступать к третьему пункту.
3. Сообразить, на что надо умножить обе части уравнения, чтобы все дроби исчезли полностью.
И тут разложение на множители тоже здорово играет на руку!
Но чтобы сразу сократить все дроби, надо скомбинировать такое выражение, которое одинаково хорошо делится и на х(2-х), и на х(2+х), и на (2-х)(2+х).
Вот оно, это выражение:
Как же я до него додумался? Очень просто: составил произведение всех неповторяющихся множителей всех знаменателей. Чтобы ничего не забыть и лишнего не взять.) Приступаем к четвёртому пункту:
4. Выполнить это самое умножение и решить новое уравнение, уже безо всяких дробей. Получить решения (кандидаты в ответ).
И снова, чтобы не заплутать в трёх соснах, используем скобки:
Производим умножение. Большие скобки раскрываем, малые — не трогаем!
Сокращаем все дроби:
Всё. От дробей избавились. Как обычно, раскрываем оставшиеся скобки, приводим подобные и собираем все члены слева:
Помним, что минус впереди крайне неудобен, посему умножаем всё на (-1):
Решаем простенькое квадратное уравнение и получаем корни:
Нашли кандидатов в ответ. Самое время вспомнить про ОДЗ. Про самый последний пункт:
5. Вспомнить про ОДЗ и состыковать найденные решения с условиями ОДЗ. Те решения, которые не входят в ОДЗ, безжалостно выбросить. Записать окончательный ответ.
Сопоставляем и… Оп-па! А ведь двойка — запретное значение! Нас не проведёшь! ОДЗ — штука жёсткая. В отвал двойку!
Окончательный ответ: х = 3.
Именно так и решаются все дробные уравнения. В пять шагов. Зачем же я распинался, рассказывая целый урок про избавление от дробей, затем ещё пол-урока про ОДЗ? Мог бы сразу дать общий алгоритм и соответствующий пример!
На этот вопрос отвечу так. Если бы вы знали, сколько народу спотыкается на применении тупо заученного алгоритма! А уж при малейшем отклонении от шаблона простой пример становится вообще нерешаемым… Если понимать смысл, то шанс решить есть всегда. Понимание всегда побеждает механическую память.)
Вот, собственно, и всё, что я хотел сказать. И напоследок очередная порция примеров для самостоятельного решения.
Ответы (по традиции, в беспорядке):
Всё совпало! Поздравляю! У вас иксов побольше будет? Хм… Про ОДЗ не забыли, случаем? Кое-какие корни выбрасывать надо! ОДЗ учли, а всё равно не выходит? Да-а-а… Проблемка. Такие уравнения надо уметь решать: слишком уж они популярны во многих темах математики. Особенно — в текстовых задачках! Но не отчаивайтесь!
Перечитайте этот и предыдущий уроки ещё раз и прогуляйтесь по смежным темам: разложение на множители, квадратные уравнения, линейные уравнения и (особенно!) тождественные преобразования уравнений. И всё получится. Я в вас верю!)