Как тригонометрия используется в физике
Как тригонометрия используется в физике
Тригонометрия в физике.
Автор работы награжден дипломом победителя III степени
Актуальность: Данная тема, бесспорно, является актуальной. Тригонометрия использовалась людьми за много лет до нашей эры, уже тогда без знания этой науки было невозможно построить дом, а астрономам не удавалось провести различные расчеты. Спустя тысячелетия ничего не изменилось, тригонометрия по-прежнему остается одной из самых нужных наук, поэтому ее основы должен знать каждый человек, для того чтобы производить расчеты и иметь представление о самых элементарных функциях, так как тригонометрия заставляет думать логически и концентрирует наше внимание.
Цель: Определение связи тригонометрии с окружающим миром.
1.Рассмотреть историю возникновения и развития тригонометрии.
2.Показать на примерах практическое применение тригонометрии в физике.
3.Раскрыть на примерах возможности использования тригонометрических функций.
Гипотеза: Большинство физических явлений природы, физиологических процессов, закономерностей в музыке и искусстве можно описать с помощью тригонометрии и тригонометрических функций.
Практическая значимость: проект может использоваться в качестве теоретического курса в качестве дополнения, закрепления уже пройденного материала или на внеурочных занятиях.
1.История возникновения тригонометрии
Зачатки тригонометрии можно найти в математических рукописях древнего Египта, Вавилона и древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.
От вавилонской математики ведёт начало привычное нам измерение углов градусами, минутами и секундами (введение этих единиц в древнегреческую математику обычно приписывают Гипсиклу, II век до н. э.).
Среди известных вавилонянам теорем была, например, такая: вписанный угол, опирающийся на диаметр круга — прямой. Главным достижением этого периода стало соотношение, позже получившее название теоремы Пифагора. Неизвестно, знали ли общую формулировку теоремы древние египтяне, но прямоугольный «египетский треугольник» со сторонами 3, 4 и 5 был там хорошо известен и широко использовался.
Общее и логически связное изложение тригонометрических соотношений появилось в древнегреческой геометрии. Греческие математики ещё не выделяли тригонометрию как отдельную науку, для них она была частью астрономии. Впервые само слово тригонометрия встречается в 1505 году в заглавии книги немецкого математика Питискуса.
Основным достижением античной тригонометрической теории стало решение в общем виде задачи «решения треугольников», то есть нахождения неизвестных элементов треугольника, исходя из трёх заданных его элементов (из которых хотя бы один является стороной).
В данном случае измерение треугольников следует понимать как решение треугольников, т. е. определение сторон, углов и других элементов треугольника, если даны некоторые из них.
Возникновение тригонометрии связано с землемерением, астрономией и строительным делом.
Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10′ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.
Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес.
Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.
Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще.
Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.
Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс, котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.
Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OМ и положительным направлением оси Ox равен α.
Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).
Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/r
Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tanα=y/x,x≠0
Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠0
Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y):
secα=r/x=1/x,x≠0
Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠0
В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету.
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.
График функции синус
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1
График функции косинус
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1
График функции тангенс y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞
Старт в науке
Учредителями Конкурса являются Международная ассоциация учёных, преподавателей и специалистов – Российская Академия Естествознания, редакция научного журнала «Международный школьный научный вестник», редакция журнала «Старт в науке».
Как тригонометрия используется в физике
Исследовательские работы и проекты
Тригонометрия в разных сферах жизни человека
1. История тригонометрии
Сам термин, давший название этому разделу математики, впервые был обнаружен в заголовке книги под авторством немецкого ученого-математика Питискуса в 1505 году. Слово «тригонометрия» имеет греческое происхождение и означает «измеряю треугольник».
2. Тригонометрия в физике
В технике и окружающем нас мире часто приходится сталкиваться с периодическими (или почти периодическими) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям.
Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения. Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения.
Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f(t). Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту или по струне.
Примерами простых колебательных систем могут служить груз на пружине или математический маятник (рис.1).
Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебаниясовершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.
3.Тригонометрия в астрономии
4. Тригонометрия в медицине
Биоритмы подразделяют на физиологические, имеющие периоды от долей секунды до нескольких минут и экологические,по длительности совпадающие с каким либо ритмом окружающей среды. К ним относят суточные, сезонные, годовые, приливные и лунные ритмы. Основной земной ритм – суточный, обусловлен вращением Земли вокруг своей оси, поэтому практически все процессы в живом организме обладают суточной периодичностью.
Множество экологических факторов на нашей планете, в первую очередь световой режим, температура, давление и влажность воздуха, атмосферное и электромагнитное поле, морские приливы и отливы, под влиянием этого вращения закономерно изменяются.
Мы на семьдесят пять процентов состоим из воды, и если в момент полнолуния воды мирового океана поднимаются на 19 метров над уровнем моря и начинается прилив, то вода, находящаяся в нашем организме так же устремляется в верхние отделы нашего тела. И у людей с повышенным давлением часто наблюдаются обострения болезни в эти периоды, а натуралисты, собирающие лекарственные травы, точно знают в какую фазу луны собирать «вершки – (плоды)», а в какую – «корешки».
Эмоциональный ритм – в периоды его активности повышается чувствительность, улучшается настроение. Человек становится возбудимым к различным внешним катаклизмам. Если у него хорошее настроение, он строит воздушные замки, мечтает влюбиться и влюбляется. При снижении эмоционального биоритма происходит упадок душевных сил, пропадает желание, радостное настроение.
Теория трех ритмов
Тригонометрия встречается и в природе. Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
При полёте птицы траектория взмаха крыльев образует синусоиду.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси,медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии.
Формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.
Тригонометрия
Тригонометрия важна при использовании диаграмм свободного тела, помогающих визуально отобразить сложные физические проблемы.
Задача обучения
Объяснить, в чем состоит польза тригонометрии при вычислении горизонтальных и вертикальных компонентов сил.
Основные пункты
Важно вычислить проблему и неизвестные, после чего отобразить их на диаграмме свободного тела.
Законы конуса и синуса применимы для вычисления вертикальной и горизонтальной составляющих различных элементов диаграммы.
Диаграммы свободного тела пользуются геометрией и векторами для визуального отображения проблем физического плана.
Термин
Тригонометрия – математическая область, изучающая соотношение сторон и углов в треугольниках. На этой основе выводятся тригонометрические функции.
Тригонометрия и решение физических проблем
В физике большая часть проблем разрешается намного быстрее, если применяется диаграмма свободного тела функции тригонометрии. Они используют геометрию и векторы, чтобы отобразить ситуацию в визуальном плане. Также при помощи тригонометрии вычисляют горизонтальные и вертикальные составляющие сил и объектов. Диаграммы приносят огромную пользу, если есть неизвестные. Они справляются со статистическими и динамическими проблемами.
Штанга отклоняется от стены и удерживается нитью
Когда мы рисуем диаграммы свободного тела, то не всегда получается добиться идеальной параллельности или перпендикулярности. Когда сила или объект не действуют параллельно оси х или y, то можно применять тригонометрию, чтобы проанализировать все действия.
С готовой диаграммой можно применять знания геометрии, а законы синуса и косинуса математически и численно отображают горизонтальные и вертикальные составляющие
Стержень АВ шарнирно прикреплен к «А» от стены и удерживается в стабильном состоянии при помощи нити. Это своеобразное упражнение, которое учит, как создавать диаграммы свободного тела. Чтобы сделать все проще, силу F выражаем через горизонтальные и вертикальные параметры. Игнорирование прочих элементов поможет сформировать финальную диаграмму.
Как тригонометрия используется в физике
Тригонометрия
Тригонометрия в жизни
ТРИГОНОМЕТРИЯ В НАШЕЙ ЖИЗНИ
Часто с синусами и косинусами приходится сталкиваться геодезистам. Они имеют специальные инструменты для точного измерения углов. При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности.
Зачатки тригонометрии можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.
Несколько десятилетий спустя Клавдий Птоломей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике. Среди прочего, описана стереографическая проекция, исследованы несколько практических задач, например: определить высоту и азимут небесного светила по его склонению и часовому углу. С точки зрения тригонометрии, это значит, что надо найти сторону сферического треугольника по другим двум сторонам и противолежащему углу.
· точного определения времени суток;
· вычисления будущего расположения небесных светил, моментов их восхода и заката, затмений Солнца и Луны ;
· нахождения географических координат текущего места;
· вычисления расстояния между городами с известными географическими координатами.
Гномон— древнейший астрономический инструмент, вертикальный предмет (стела, колонна, шест),
Так, под котангенсом понималась длина тени от вертикального гномонавысотой 12 (иногда 7) единиц; первоначально эти понятия использовались для расчёта солнечных часов. Тангенсом называлась тень от горизонтального гномона. Косекансом и секансом назывались гипотенузы соответствующих прямоугольных треугольников (отрезки AO на рисунке слева)
Широко используется тригонометрия в строительстве, а особенно в архитектуре. Большинство композиционных решений и построений
Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой. Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности. Велось
Модель боритмов можно построить с помощью тригонометрических функций. Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
Формула сердца. В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии. Формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.
Также тригонометрия помогает нашему мозгу определять расстояния до объектов.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Строго говоря, идея «измерения углов» не является новой. Еще художники Древнего Китая рисовали удаленные объекты выше в поле зрения, несколько пренебрегая законами перспективы. Сформулировал теорию определения расстояния по оценке углов арабский ученый XI века Альхазен. После долгого забвения в середине прошлого столетия идею реанимировал психолог Джеймс
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму
d B и измерим длину с отрезка АВ. Затем измерим, например
с помощью астролябии, углы A и B . Эти данные, т.е. c , a и b
позволяют решить треугольник АВС и найти искомое
Затем с помощью теоремы синусов находим d .
Немного о тригонометрии в нашей жизни.
Содержимое разработки
Учитель математики: Шевцова В.В.
Зачатки тригонометрии обнаружены в
сохранившихся документах Древнего Вавилона, где астрономия достигла значительного развития. Вавилонские ученые составили одну из первых карт звездного неба. Они умели предсказывать солнечные и лунные затмения.
Некоторые сведения тригонометрического
характера встречаются и в старинных
памятниках других народов древности.
История тригонометрии как науки о соотношениях между углами и сторонами треугольника и других геометрических фигур охватывает более двух тысячелетий. Большинство таких соотношений нельзя выразить с помощью обычных алгебраических операций, и поэтому понадобилось ввести особые тригонометрические функции, первоначально оформлявшиеся в виде числовых таблиц.
Историки полагают, что тригонометрию создали древние астрономы; немного позднее её стали использовать в геодезии и архитектуре. Со временем область применения тригонометрии постоянно расширялась, и в наши дни она включает практически все естественные науки, технику и ряд других областей деятельности
Первые тригонометрические таблицы были, вероятно, составлены Гиппархом
Никейским (180—125 лет до н. э.). Гиппарх был первым, кто свёл в таблицы соответствующие величины дуг и хорд для серии углов. Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд.
Замена хорд синусами стала главным достижением средневековой Индии . Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.
В процессе работы над учебным проектом «Зачем нужна тригонометрия» была создана группа физиков, которая занималась изучением проблемы «Почему мы иногда видим то, чего нет на самом деле?». Для исследования были предложены следующие вопросы: «Как устроено наше зрение и как создаются оптические иллюзии?», «Почему мы видим миражи?», «Как возникает радуга?», «Что такое полярное сияние?», «Как тригонометрия может помочь найти ответы на эти вопросы?».
Все проблемные вопросы полностью освещены. Рассмотрены различные виды оптических иллюзий, и выяснены основные причины возникновения иллюзий. Также раскрыта суть естественных (природных) оптических иллюзий – радуги, миража, северного сияния – с помощью законов физики. Выяснено, что законы оптики описываются с помощью тригонометрических функций.
Тригонометрия в музыке
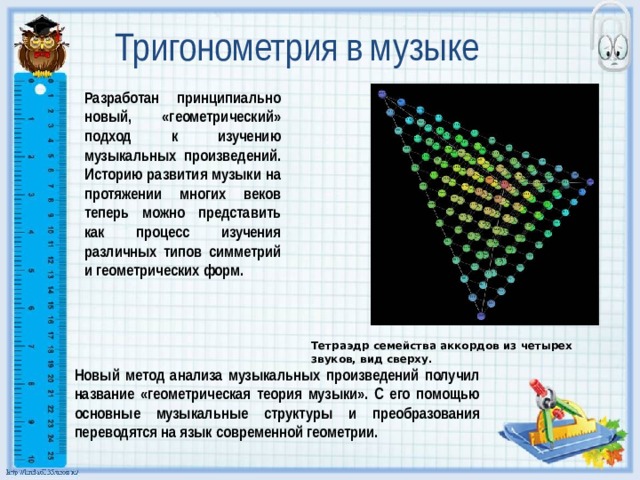
Разработан принципиально новый, «геометрический» подход к изучению музыкальных произведений. Историю развития музыки на протяжении многих веков теперь можно представить как процесс изучения различных типов симметрий и геометрических форм.
Тетраэдр семейства аккордов из четырех звуков, вид сверху.
Новый метод анализа музыкальных произведений получил название «геометрическая теория музыки». С его помощью основные музыкальные структуры и преобразования переводятся на язык современной геометрии.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Такой вывод был сделан после серии экспериментов, участникам которых предлагалось взглянуть на окружающий мир через призмы, увеличивающие этот угол. Такое искажение приводило к тому, что подопытные носители призм воспринимали удаленные объекты как более близкие и не могли справиться с простейшими тестами. Однако по прошествии 20 минут они привыкли к искаженному восприятию, и все проблемы исчезли. Это обстоятельство указывает на гибкость механизма, с помощью которого мозг приспосабливает зрительную систему к меняющимся внешним условиям.
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.
При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
Тригонометрия и тригонометрические функции повсюду!