Как треугольник достроить до параллелограмма

Равновеликие фигуры

Презентация к уроку

Цели урока: Повторить тему «Площадь параллелограмма». Вывести формулу площади треугольник, ввести понятие равновеликих фигур. Решение задач по теме «Площади равновеликих фигур».

Ход урока

I. Повторение.

1) Устно по готовому чертежу вывести формулу площади параллелограмма.

2) Какова зависимость между сторонами параллелограмма и высотами, опущенными на них?

(по готовому чертежу)

зависимость обратно пропорциональная.

3) Найти вторую высоту (по готовому чертежу)

4) Найти площадь параллелограмма по готовому чертежу.

Решение:

5) Сравните площади параллелограммов S1, S2, S3. (Они имеют равные площади, у всех основание a и высота h).

Определение: Фигуры, имеющие равные площади, называются равновеликими.

II. Решение задач.

1) Доказать, что всякая прямая, проходящая через точку пересечения диагоналей, делит его на 2 равновеликие части.

Решение:

2) В параллелограмме ABCD CF и CE высоты. Доказать, что AD ∙ CF = AB ∙ CE.

3) Дана трапеция с основаниями a и 4a. Можно ли через одну из её вершин провести прямые, разбивающие трапецию на 5 равновеликих треугольников?

Решение: Можно. Все треугольники равновеликие.

4) Доказать, что если на стороне параллелограмма взять точку A и соединить её с вершинами, то площадь получившегося треугольника ABC равна половине площади параллелограмма.

Решение:

5) Торт имеет форму параллелограмма. Малыш и Карлсон делят его так: Малыш указывает на поверхности торта точку, а Карлсон по прямой, проходящей через эту точку, разрезает торт на 2 куска и один из кусков забирает себе. Каждый хочет получить кусок побольше. Где Малыш должен поставить точку?

Решение: В точке пересечения диагоналей.

6) На диагонали прямоугольника выбрали точку и провели через неё прямые, параллельные сторонам прямоугольника. По разные стороны образовались 2 прямоугольника. Сравните их площади.

Решение:

III. Изучение темы «Площадь треугольника»

«Найти площадь треугольника, у которого основание a, а высота h».

Ребята, используя понятие равновеликих фигур, доказывают теорему.

Достроим треугольник до параллелограмма.

Площадь треугольника равна половине площади параллелограмма.

Задание: Начертите равновеликие треугольники.

Используется модель (из бумаги вырезаны 3 цветных треугольника и склеены у оснований).

Упражнение №474. «Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой».

У треугольников одинаковые основания a и одна и та же высота h. Треугольники имеют одинаковую площадь

Вывод: Фигуры, имеющие равные площади, называются равновеликими.

Вопросы к классу:

IV. Шаг вперёд!

На доске написаны задания по выбору:

1. «Разрежьте треугольник двумя прямыми линиями так, чтобы можно было из частей сложить прямоугольник».

Решение:

2. «Разрежьте прямоугольник по прямой линии на 2 части, из которых можно сложить прямоугольный треугольник».

Решение:

3) В прямоугольнике проведена диагональ. В одном из получившихся треугольников проведена медиана. Найдите соотношения между площадями фигур .

Решение:

Ответ:

3. Из олимпиадных задач:

«В четырёхугольнике ABCD точка E- середина AB, соединена с вершиной D, а F – середина CD, с вершиной B. Доказать, что площадь четырёхугольника EBFD в 2 раза меньше площади четырёхугольника ABCD.

Решение: провести диагональ BD.

Упражнение №475.

«Начертите треугольник ABC. Через вершину В проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади».

Использовать теорему Фалеса (разделить АC на 3 равные части).

V. Задача дня.

Для неё отвела крайнюю правую часть доски, на которой пишу задачу сегодняшнего дня. Ребята могут решать её, а могут и не решать. На уроке данную задачу мы сегодня не решаем. Просто те, кому они интересны, могут списать её, решить её дома или в перемену. Обычно уже в перемену многие ребята начинают решать задачу, если решили, то показывают решение, и я фиксирую это в специальной таблице. На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача).

«В параллелограмме вырезан параллелограмм. Разделите оставшуюся часть на 2 равновеликие фигуры».

Решение: Секущая AB проходит через точку пересечения диагоналей параллелограммов O и O1.

Дополнительные задачи (из олимпиадных задач):

1) «В трапеции ABCD (AD || BC) вершины A и B соединены с точкой M – серединой стороны CD. Площадь треугольника ABM равна m. Найти площадь трапеции ABCD».

Решение:

Треугольники ABM и AMK – равновеликие фигуры, т.к. AM – медиана.
S_∆ABK = 2m, ∆BCM = ∆MDK, S_ABCD = S_∆ABK = 2m.

2) «В трапеции ABCD (AD || BC) диагонали пересекаются в точке O. Доказать, что треугольники AOB и COD равновеликие».

Решение:

S_∆BCD = S_∆ABC, т.к. у них общее основание BC и одинаковая высота.

3) Сторона АВ произвольного треугольника АВС продолжена за вершину В так, что ВР = АВ, сторону АС за вершину А так, что АМ = СА, сторону ВС за вершину С так, что КС = ВС. Во сколько раз площадь треугольника РМК больше площади треугольника АВС?

Решение:

В треугольнике МВС: МА = АС, значит, площадь треугольника ВАМ равна площади треугольника АВС. В треугольнике АРМ: ВР = АВ, значит, площадь треугольника ВАМ равна площади треугольника АВР. В треугольнике АРС: АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК: ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК: ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,

Ответ: Площадь треугольника МРК в 7 раз больше площади треугольника АВС.

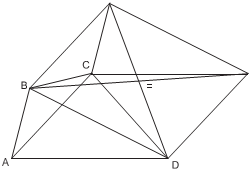
4) Сцепленные параллелограммы.

2 параллелограмма расположены так, как показано на рисунке: они имеют общую вершину и ещё по одной вершине у каждого из параллелограммов лежит на сторонах другого параллелограмма. Доказать, что площади параллелограммов равны.

Решение:

и , значит,

Список использованной литературы:

Источник

Как треугольник достроить до параллелограмма

§2. Площадь треугольника. Метод площадей

В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.

При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.

Для примера, рассмотрим два треугольника:

`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;

`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;

Надо найти площадь и радиус описанной окружности.

Для треугольника `ABC` удобен ход решения такой:

`p=1/2(AB+BC+AC)=21`, по формуле Герона

`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)

тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):

тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).

Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:

$$ 2.<1>^<○>$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то

$$ 2.<2>^<○>$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):

$$ 2.<3>^<○>$$. Площади подобных треугольников относятся как квадраты их

сходственных сторон, т. е. если `Delta ABC

DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.

Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).

Обратим внимание на важное свойство медиан треугольника.

Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.

Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.

Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.

2. Через точку `D` проведём прямую `DL«|\|«AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL«|\|«AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.

По той же теореме (`/_DCB`, `OK«|\|«DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.

3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.

(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`

`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).

Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.

Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).

Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).

В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.

Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.

Значит и `S_(ABC)=6sqrt3`.

В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.

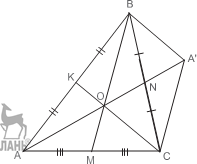
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.

По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.

Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:

`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.

Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.

В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.

Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.

Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.

Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.

Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:

Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.

Проведём два примера, в каждом выведем полезную формулу.

В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.

Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:

называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.

Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.

Считаем площадь `S_0` четырёхугольника `ABI_aC`:

`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда

Источник

Метод параллельного переноса. Построить трапецию по четырём сторонам.

Задача 1.

Построить трапецию по четырём сторонам.

И д е я. Произвести параллельный перенос боковой стороны трапеции.

У к а з а н и е. После параллельного переноса боко- вой стороны трапеции получится треугольник, ко- торый легко построить по трём сторонам.

Задача 2.

Между двумя окружностями провести отрезок, делящийся пополам в данной точ- ке A.

И д е я. Предположить, что искомый отрезок построен, и воспользоваться парал- лельным переносом.

Задача может иметь одно, два или ни одного решения.

Задача 3.

И д е я. Предположить, что треугольник построен, и провести дополнительное построение.

Общая последовательность действий такова.

2) Вершину A получим, отложив на прямой OA

3) Вершину C получим, отложив на прямой BN

Задача 4.

Через точку A внутри угла провести прямую так, чтобы отрезок, заключённый между сторо- нами, делился точкой A пополам.

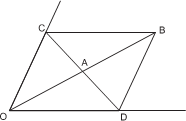
И д е я. Диагонали параллелограмма делятся точкой пересечения пополам.

Ук азани е. Отложить на прямой OA отрезок AB = OA. Через точку B провести прямые, па- раллельные сторонам угла.

Так как диагонали параллелограмма точкой пересечения делятся пополам, то

CA = AD. Следовательно, CD – искомая прямая.

Задача 5.

Построить трапецию, зная диагонали, угол между ними и одну из боковых сторон.

И д е я. Использовать параллельный перенос од- ной из диагоналей трапеции.

У к а з а н и е. Треугольник ACE легко постро- ить по двум сторонам и углу между ними.

Р е ш е н и е. Пусть даны длины диагоналей AC и BD и длина боковой стороны

Задача 6.

Построить четырёхугольник, зная две диагонали, две противолежащие стороны и угол между ними.

И д е я. Использовать параллельный перенос одной из диагоналей четырёхуголь- ника.

У к а з а н и е. Треугольник XCD можно по- строить по двум сторонам и углу между ними. У к а з а н и е. Треугольник BDX легко по- строить по трём сторонам.

Задача 7.

Через данную точку M провести прямую так, чтобы разность расстояний до неё от двух данных точек A и B была равна данной длине.

И д е я. Предположить, что прямая проведена, опустить на неё перпендикуляры из данных точек и использовать параллельный перенос.

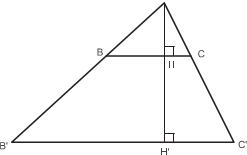
Задача 8.

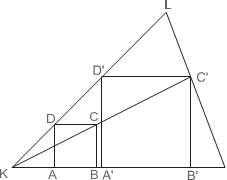
В данный остроугольный треугольник вписать прямоугольник с наименьшей диа- гональю (одна сторона прямоугольника лежит на основании треугольника).

И д е я. Вершину треугольника перенести параллельно основанию так, чтобы по- лучился прямоугольный треугольник.

Диагональ прямоугольника K L M A будет принимать минимальное значение в случае, ко-

вести AL ⊥ BC и построить прямоугольник

K L M A с такой диагональю. Этот прямоуголь-

ник и будет искомым прямоугольником.

Задача 9.

Даны три параллельные прямые. Провести через данную точку секущую так, что- бы разность отрезков между параллелями была равна заданной величине.

И д е я. Использовать методы симметрии и параллельного переноса.

Задача 10.

У к а з а н и е. Треугольник ACE можно построить по основанию, высоте и из- вестному углу.

сечку циркулем из C на прямой AE радиусом, равным длине боковой стороны

Задача 11.

Построить треугольник по b, c и m _a .

И д е я. Использовать вспомогательное построение: достроить треугольник до па- раллелограмма.

У к а з а н и е. Построить ΔABA по трём известным сторонам.

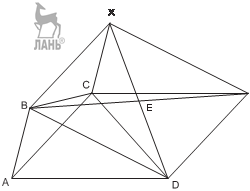
Задача 12.

Построить четырёхугольник, зная его стороны и отрезок, соединяющий середины двух противоположных сторон.

И д е я. Использовать вспомогатель- ный параллелограмм, стороны кото- рого параллельны и равны диагона- лям искомого четырёхугольника.

У к а з а н и е. Построить ΔBCY по трём сторонам.

У к а з а н и е. Построить ΔCXD по медиане и двум сторонам.

В теоретической части было показано, что диагонали параллелограмма BXY D

вдвое больше средних линий исходного четырёхугольника.

Задача 13.

Построить четырёхугольник, зная четыре его стороны и угол между двумя про- тивоположными сторонами.

И д е я. Использовать вспомогательный параллелограмм, стороны которого па- раллельны и равны диагоналям искомого четырёхугольника.

У к а з а н и е. Построить ΔCXD по двум сторонам и углу между ними.

Угол XCD равен углу меж- ду прямыми, содержащими сторо- ны AB и CD (см. теоретическую часть). Следовательно, в ΔCXD стороны CX (CX = AB ) и CD равны сторонам исходного четырёх-

532 Указания и решения

Задача 14.

Построить биссектрису угла, вершина которого недоступна.

И д е я. Предположить, что биссектриса построена, и провести из любой точки биссектрисы две прямые, параллельные сторонам угла.

У к а з а н и е. Расстояния от построенных прямых до соответствующих сторон уг- ла будут одинаковыми.

В силу равенства углов при параллель- ных прямых биссектрисой построенного угла будет также прямая m. Отметим, что расстояния между параллельными прямы- ми будут равными.

Следовательно, если вершина O недо- ступна, то надо провести две прямые на

равном расстоянии от сторон исходного угла и для угла с уже доступной верши- ной построить биссектрису.

Задача 15.

Даны две точки A и B и между ними две параллели m и n. Провести между этими параллелями в данном направлении отрезок CD так, чтобы сумма AC+

+ CD + BD была минимальной.

Задача 16.

XY так, чтобы сумма хорд AX и BY была равна заданной величине.

У к а з а н и е. Надо построить точку Y такую, что BY + Y A имеет заданную длину, а эта зада- ча была решена в предыдущем разделе методом симметрии и спрямления.

Итак, всё свелось к построению точки Y та- кой, что BY + Y A имеет заданную длину, а эта задача была решена нами в предыдущем разделе методом симметрии и спрямления.

Задача 17.

Построить прямоугольник с данной стороной так, чтобы его стороны проходили через четыре заданные точки.

И д е я. Пусть прямоугольник построен. Проанализировать, что нам известно.

У к а з а н и е. Треугольник ACH можно построить по известной гипотенузе AC

Задача 18.

Даны две окружности и прямая. Провести параллельно этой прямой секущую, отсекающую в окружностях хорды, сумма которых равна заданному отрезку дли- ны s.

И д е я. Предположить, что искомая прямая проведена, и провести параллельный перенос одной из окружностей.

У к а з а н и е. Рассмотрим две окружности с центрами O₁ и O₂ и прямую m.

Пусть AD m и AB + CD = s. Перенести вторую окружность так, что хорда CD

Ук азани е. Пусть P и Q – основания перпендикуляров, опущенных из точек

Пусть P и Q – основания перпендику-

В целом построение выглядит следую- щем образом. Проведём через O₂ прямую параллельно m и через O₁ прямую пер-

Метод подобия

Задача 1.

Построить треугольник по двум уг- лам и высоте, проведённой из третье- го угла.

И д е я. Построить треугольник, по- добный искомому.

Задача 2.

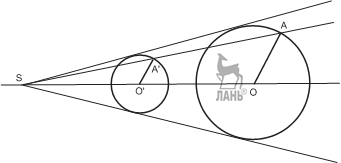
Построить окружность, касающуюся сторон данного угла и проходящую через заданную внутри него точку.

У к а з а н и е. Соединить вершину угла S с заданной точкой A.

З а м е ч а н и е. Если через A обозначить вторую точку пересечения прямой SA со вспомогательной окружностью, то, действуя аналогично, получим вторую окружность, проходящую через точку A и касающуюся сторон угла.

Задача 3.

Дан треугольник ABC со сторонами AB = 5, BC = 6, AC = 7. Построить точку S BC, точку Q AC и точку P AB так, чтобы треугольник SQP был равносторонним.

И д е я. Построить треугольник (со вписанным в него равносторонним треуголь- ником), подобный данному, а потом с помощью гомотетии преобразовать вписан- ный треугольник в искомый.

Заметим, что треугольники ABC и

AB C подобны с коэффициентом по-

применим гомотетию с этим коэффи-

(это мы умеем делать). Ана-

Задача 4.

В данный треугольник вписать квадрат.

И д е я. Построить вспомогательный квадрат и воспользоваться преобразованием гомотетии.

ABCD такой, что A, B KM, D KL. Ук азани е. Провести прямую KC до пересечения со стороной ML.

Задача 5.

Задача 6.

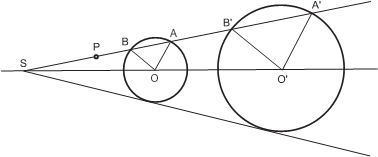
Через данную точку провести прямую, отсекающую от двух данных окружностей хорды, пропорциональные их радиусам.

И д е я. Использовать свойства центра подобия окружностей.

У к а з а н и е. Воспользоваться тем, что любая секущая, проведённая через центр подобия окружностей, отсекает от окружностей хорды, пропорциональные ради- усам.

Р е ш е н и е. Воспользуемся тем, что любая секущая, проведённая через центр подобия окружностей, пересекает окружности таким образом, что треугольники ABO и A B O являются гомотетическими. Проведём через центр подобия S и данную точку P прямую. Из подобия треугольников ABO и A B O следует про- порциональность соответствующих отрезков.

Задача 7.

И д е я. Использовать преобразование гомотетии.

Задача 8.

Даны три точки A, B и C, не лежащие на одной прямой. Провести прямую, пересекающую отрезок AC в точке X, а отрезок BC в точке Y таким образом, что AX = XY = Y B.

У к а з а н и е. Четырёхугольник AX Y B (AX = X Y = Y B = d ) подобен искомому.

Проведём прямую через точки A и Y до пересечени

Источник