Как теорема штейнера проверяется экспериментально
Проверка теоремы Штейнера методом крутильных колебаний.
Для однородных и симметричных тел справедлива теорема Штейнера, которая формулируется следующим образом:
момент инерции I относительно произвольной оси равен сумме момента инерции I0 ’ относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела m на квадрат расстояния d между осями:

Справедливость теоремы Штейнера можно проверить при помощи трифилярного подвеса, для чего необходимо иметь два совершенно одинаковых тела. Оба тела располагают симметрично на платформе и определяют их момент инерции при таком расположении. Половина этой величины и будет давать момент инерции одного тела, находящегося на фиксированном расстоянии от оси вращения. Зная это расстояние, массу тела и момент инерции тела, положенного в центре платформы, можно проверить теорему Штейнера
Тела на платформе необходимо класть строго симметрично так, чтобы не было перекоса платформы, для чего на платформе нанесены цилиндрические окружности на определенном расстоянии друг от друга.
Измерения.
При измерениях недопустимо пользоваться амплитудами колебаний, большими 5-6 градусов. Все данные измерений и расчетов свести в таблицу, проверить соотношение (2).
В работе использовать систему единиц СИ.
Период 
Контрольные вопросы.
1. Что называется моментом инерции тела? В каких единицах измеряется момент инерции тела?
2. Выведите рабочую формулу. Какие упрощающие предположения следует использовать при выводе?
3. Справедлив ли указанный метод при определении момента инерции, если его центр инерции не лежит на оси вращения системы?
4. Сформулируйте и докажите теорему Штейнера.
1. Савельев И.В. Курс общей физики. Т.Г. Наука. 1977.§§ 36-39.
2. Сивухин Д.В. Общий курс физики. Т.I. Наука. 1974. §§ 52,55-59.
КРАТКАЯ ТЕОРИЯ. Цель работы: Проверить теорему Штейнера



ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛ
И ПРОВЕРКА ТЕОРЕМЫ ШТЕЙНЕРА
С ПОМОЩЬЮ ТРИФИЛЯРНОГО ПОДВЕСА
Цель работы: Проверить теорему Штейнера.
Принадлежности: Трифилярный подвес, секундомер, штангенциркуль, линейка, исследуемые тела (два стальных цилиндра).
КРАТКАЯ ТЕОРИЯ
Моментом инерции материальной точки называют физическую величину, определяемую произведением массы точки mна квадрат расстояния ее r от оси вращения:
Всякое тело можно рассматривать как совокупность некоторого числа материальных точек. Момент инерции тела равен сумме моментов инерции всех его точек:
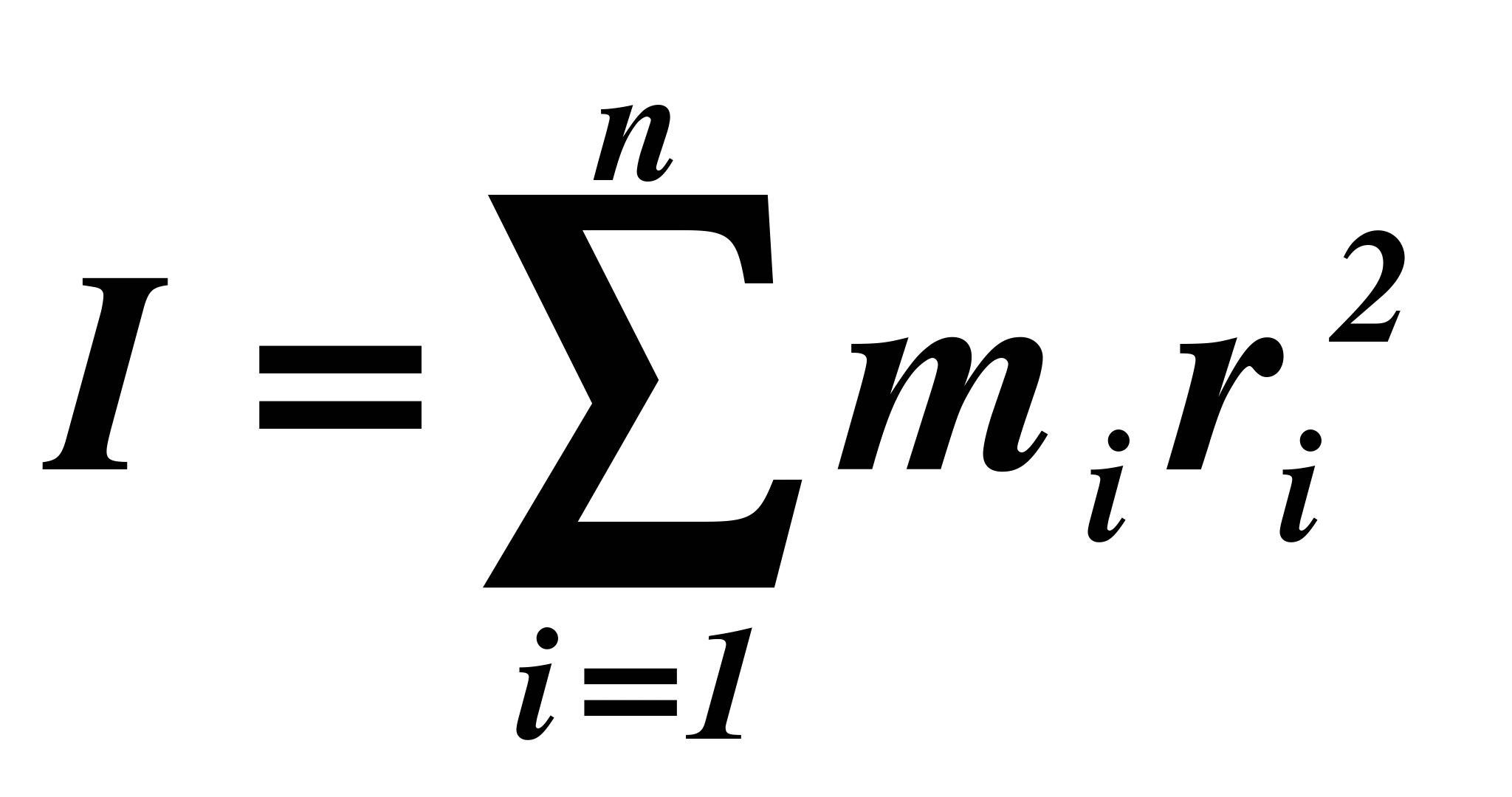
Момент инерции является удобной характеристикой инертности тела, проявляемой при вращательном движении. Он входит в ряд важных соотношений, характеризующих твердое тело, вращающееся относительно неподвижной свободной оси. Например, в соотношения, определяющие момент импульса и кинетическую энергию тела

Момент инерции входит и во второй закон Ньютона, описывающий вращение твердого тела:
` 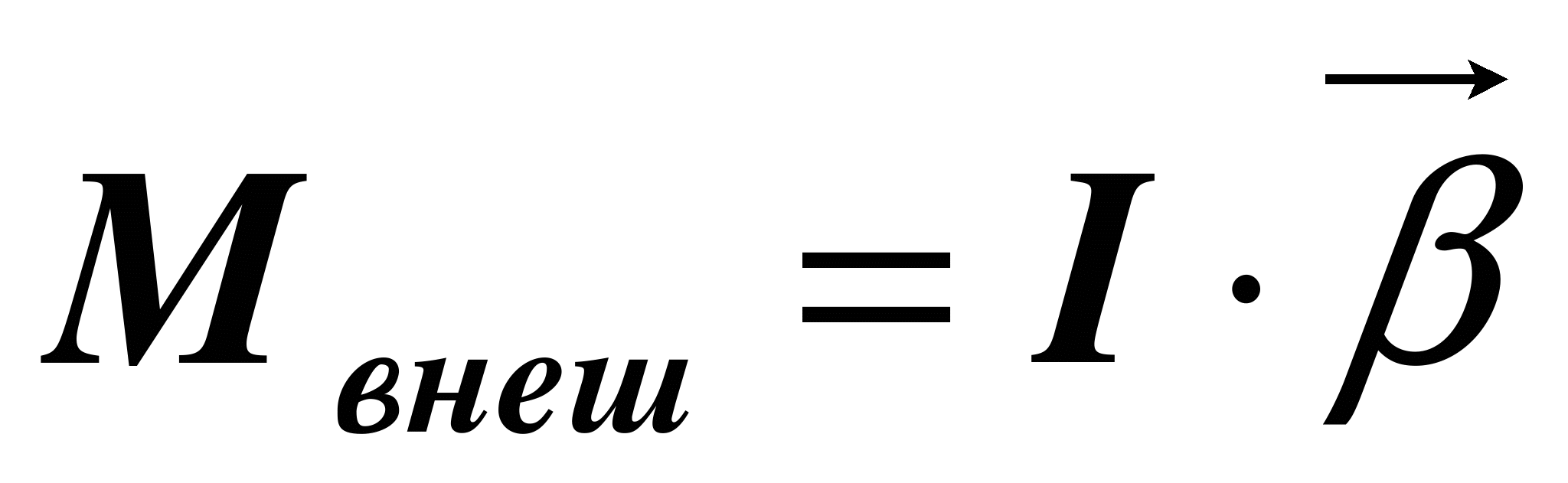
и в ряд других формул, определяющих период колебаний физического и крутильного маятников:
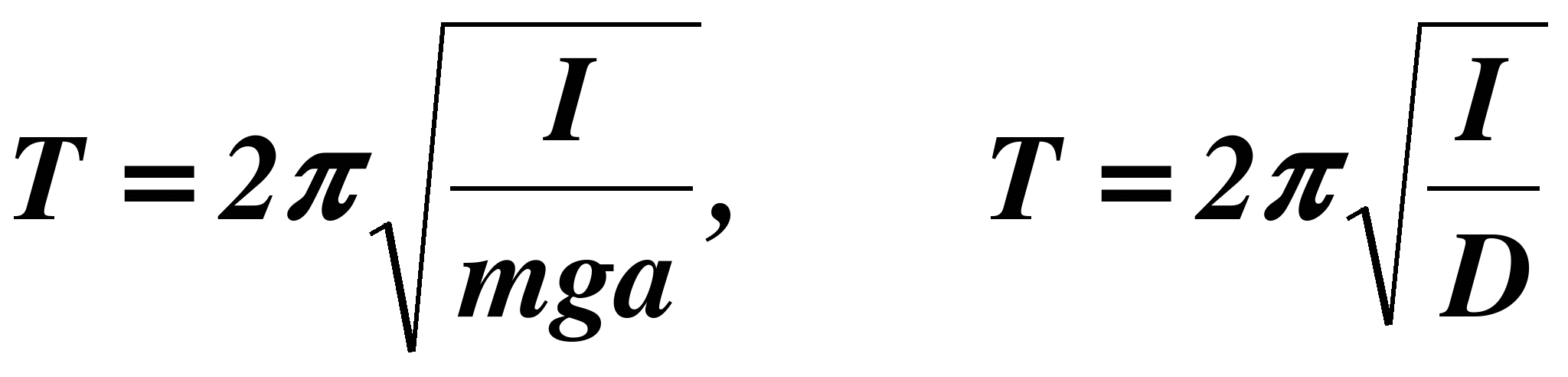
Поэтому определение момента инерции твердых тел имеет большое практическое значение. Чаще всего момент инерции тел определяется опытным путем. В данной работе для этого используется трифилярный подвес, совершающий крутильные колебания.
Известно, что при небольших углах закручивания трифилярный подвес (рис.2) совершает гармонические колебания, период которых определяется формулой:
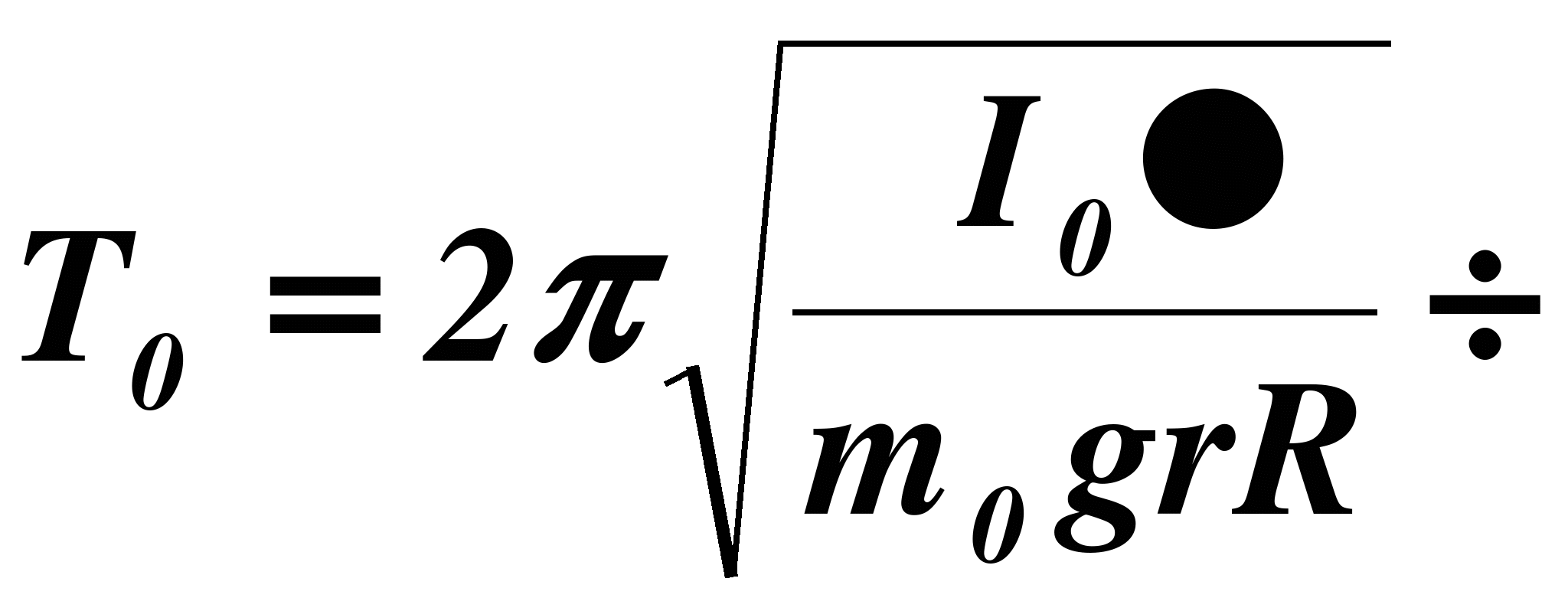
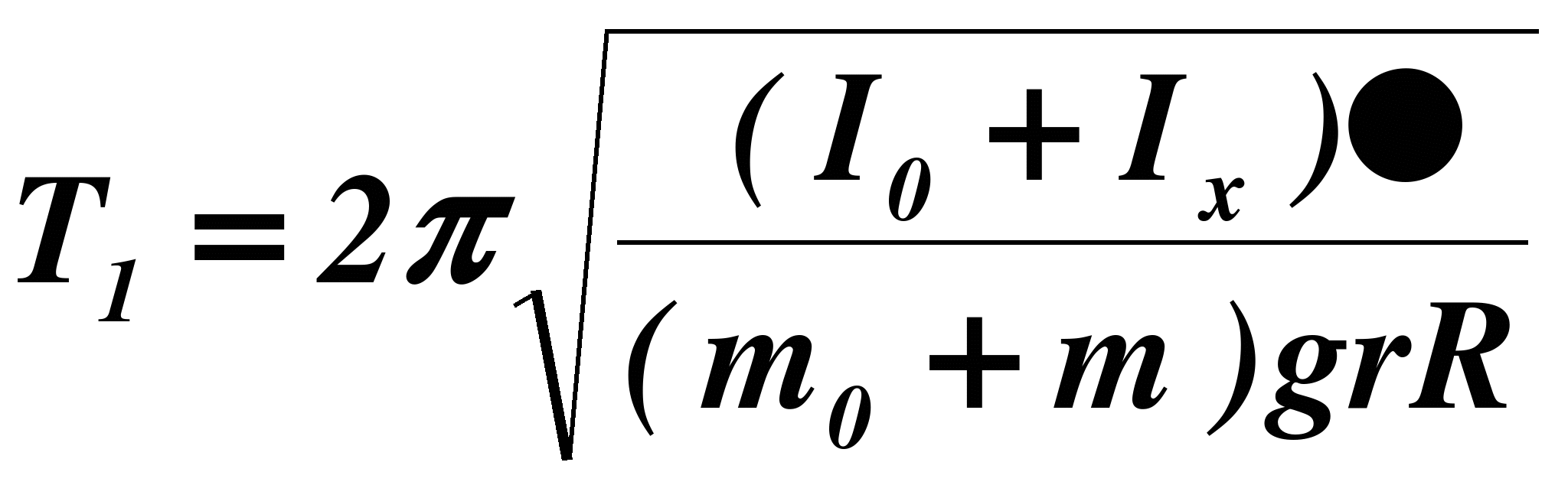
Из приведенных формул (1) и (2) легко получить формулу для момента инерции исследуемого тела:
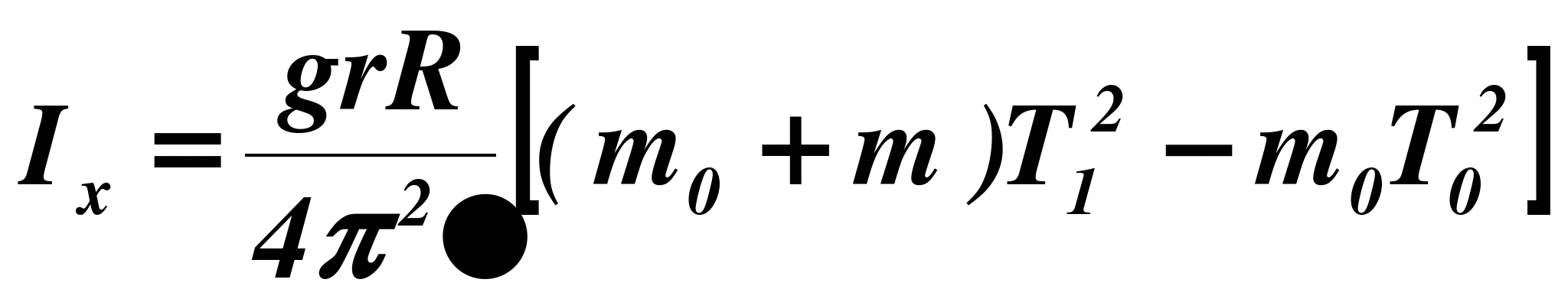
Момент инерции тела относительно произвольной оси I превосходит его момент инерции относительно оси, проходящей через центр масс тела Ic параллельно данной, на величину ma 2 :
Используя теорему Штейнера, подсчитаем момент инерции прямого однородного кругового цилиндра массы m и радиуса R относительно оси, совпадающей с его образующей:
поэтому Iобр =1/2 mR 2 + mR 2 = 3/2 mR 2 ;
Из полученного следует, что момент инерции цилиндра относительно образующей превосходит его момент инерции относительно оси, проходящей через центр масс, в 3 (три) раза.
Главной целью данной работы является экспериментальная проверка этого вывода.
Проверка теоремы Штейнера
Теорема Штейнера утверждает, что момент инерции тела J’1 относительно произвольной оси О1О2 (рис.2) равен сумме момента инерции J1 относительно оси, параллельной данной и проходящей через центр масс тела точку О (ос О’1О’2) и произведения массы тела m на квадрат расстояния между осями а 2 :
Для экспериментальной проверки теоремы Штейнера используют два одинаковых тела (сплошных цилиндра), массы которых равны m.
1. Поместить эти тела одно на другое строго по центру платформы и привести систему в крутильные колебательные движения.
2. Определить период колебаний, используя методику упражнения 1.
3. Рассчитать момент инерции двух цилиндрических тел J2 (с учетом платформы) по формуле (8).
4. Рассчитать момент инерции двух тел J1, расположенных на оси вращения платформы как разность J1 = J2 – J0.
5. Расположить эти два тела на платформе симметрично на некотором расстоянии от оси вращения, определить период колебаний.
6. Рассчитать момент инерции двух тел, находящихся на некотором расстоянии от оси вращения (с учетом J0 платформы) J’2 по формуле (8). Особое внимание обратить на правильное определение расстояния от тел до оси вращения, используя рис.2.



 |
7. Рассчитать момент инерции двух тел, находящихся на некотором расстоянии от оси вращения J’1, как разность J’1 = J’2 – J0.
Разница в числовых значениях J’1 и J1, составляет смысл теоремы Штейнера, а именно:
где m – масса одного тела; а – расстояние от оси вращения до центра цилиндра. Измерить а штангенциркулем или линейкой, проводя измерения несколько раз.
8. Оценить погрешность этого опыта.
1. Определить момент инерции твердого тела неправильной геометрической формы, выполняя пункты упражнения 2.
2. Сделать письменный вывод по работе.
1. Что такое момент инерции? Чему он равен у произвольного тела и у тел правильной геометрической формы: диска, цилиндра, шара?
2. Вывести формулу момента инерции ненагруженной платформы.
3. От каких факторов зависит точность этих опытов? Почему необходимо пользоваться малыми углами поворота платформы при крутильных колебаниях?
4. Сформулировать теорему Штейнера и объяснить, как она проверяется в данной лабораторной работе.
5. Можно ли пользоваться предложенным методом для определения моментов инерции тел в том случае, если ось вращения платформы не проходит через их центр тяжести?
Литература.
1. Киттель Ч., Найт У., Рудерман М. Берклеевский курс физики. Т. 1. М.: Наука, 1975.
2. Матвеев А.Н. Механика и теория относительности. М.: Высшая школа, 1976.
3. Руководство к лабораторным занятиям по физике (Под ред. Л.Л. Гольдина). М.: Наука, 1964.
4. Сивухин Д.В. Общий курс физики. Т. 1. М.: Наука, 1977.
Лабораторная работа № 7
Дата добавления: 2014-11-08 ; просмотров: 829 ; Нарушение авторских прав
Как теорема штейнера проверяется экспериментально
В эксперименте используется связь между периодом колебаний крутильного маятника и его моментом инерции. В качестве маятника выбрана круглая платформа, подвешенная в поле тяжести на трех длинных нитях (трифилярный подвес). Платформа может совершать крутильные колебания вокруг вертикальной оси. На платформу помещаются тела различной формы, измеряются периоды колебаний маятника и определяются значения моментов инерции этих тел. Теорема Гюйгенса-Штейнера проверяется по соответствию между экспериментальной и теоретической зависимостями моментов инерции грузов от их расстояния до центра платформы.
Теорема Гюйгенса-Штейнера. Если момент инерции тела относительно некоторой оси вращения, проходящей через центр масс, имеет значение J0, то относительно любой другой оси, находящейся на расстоянии a от первой и параллельной ей, он будет равен
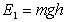 , (2.2)
, (2.2)Считая, что платформа совершает гармонические крутильные колебания, можно записать зависимость углового смещения платформы 
В момент прохождения платформы через положение равновесия (t = 0, 0.5Т. ) величина w(t) будет максимальна и равна по модулю
Из выражений (2.4) и (2.7) следует, что
а при максимальном отклонении платформы от положения равновесия
При этом закон сохранения энергии (2.8) примет вид:
откуда следует, что
Соотношение (2.15) используется в лабораторной работе для определения моментов инерции тел простой формы и подтверждения справедливости теоремы Гюйгенса-Штейнера.
Вид установки показан на рис.6. или AVI (3.8M) Отношение радиуса платформы к длине нитей подвеса составляет 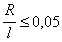
Тела на платформу необходимо класть строго симметрично, так, чтобы не было перекоса платформы. Для облегчения определения положения грузов и более точной их установки на платформе нанесены концентрические окружности на определенном расстоянии друг от друга (5 мм).
Для проверки теоремы Гюйгенса-Штейнера используют два одинаковых тела (в данной работе они имеют цилиндрическую форму). Перед каждым измерением следует остановить платформу.
Произвести взвешивание грузов.
Установить грузы в центре платформы, положив их один на другой. Создать крутильные колебания платформы. Измерить время tn нескольких колебаний (n=15-20). Данные занести в табл. 2.1.
Таблица 2.1
Расположить грузы симметрично на платформе. Провести измерения времени колебаний tn для 5-7 положений грузов, постепенно перемещая их к краям платформы. Рекомендуется перемещать грузы каждый раз на 1 см. Занести в табл.2.1 значения расстояний а от центра масс каждого тела до центра платформы, число колебаний n и значения времени этих колебаний tn.
Обработка результатов
Для каждого положения грузов определить период колебаний грузов Ti.
Для каждого положения грузов найти значения момента инерции платформы с грузами Ji по формуле (2.15). Величины l, R, r и масса платформы даются, как постоянные установки.
Полученные значения Ji наносят на график зависимости момента инерции системы тел, 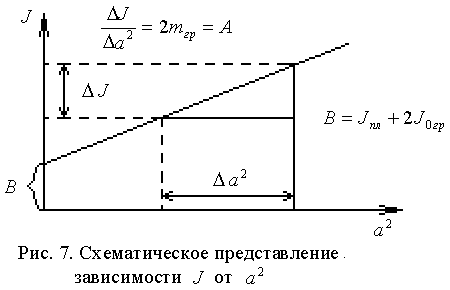
Как следует из теоремы Гюйгенса-Штейнера, этот график должен быть прямой линией, с угловым коэффициентом численно равным 2mгр, так как используются два тела с одинаковой массой mгр.
Момент инерции пустой платформы Jпл определяют по формуле 2.15. Измерить период колебаний пустой платформы Tпл. Сообщают платформе вращательный импульс и измеряют время tn некоторого числа (n=15-20) полных колебаний, что дает возможность достаточно точно определить величину периода Tпл Такие измерения проводят 3-5 раз. Полученные результаты заносят в табл. 2.2.
Таблица 2.2
Платформу поочередно нагружают исследуемыми телами таким образом, чтобы их центр масс совпадал с осью вращения платформы (совпадали отверстия в теле и на платформе). Масса этих тел известна или может быть определена с помощью взвешивания. В качестве исследуемых тел выбирают пластины, имеющие форму квадрата и равностороннего треугольника. Измеряют время tn нескольких колебаний всей системы. Для каждого тела проводят измерения 3-5 раз. Результаты измерений заносят в табл. 2.2.
Обработка результатов
По экспериментальным данным для каждого опыта найти значение величины периода крутильных колебаний 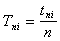
Найти средние арифметические значения и среднеквадратичные отклонения для периодов колебаний пустой платформы ( Tпл ) и платформы с исследуемыми телами ( T2 и T3 ).
Вычислить моменты инерции квадратной и треугольной пластин по формулам:
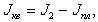 (2.16)
(2.16)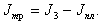 .
.Найти среднеквадратичные отклонения этих величин.
Провести сравнение экспериментально полученных значений Jкв и Jтр и с рассчитанными теоретически (см. Приложение) по формулам:
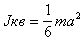 (2.17)
(2.17)для квадрата и
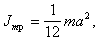 (2.18)
(2.18)Провести сопоставления величины Jпл с величиной В, полученной в упр.1, таким образом проверить соотношение 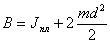
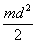
Основные итоги работы
В результате выполнения работы должна быть проведена проверка выполнения теоремы Гюйгенса-Штейнера. Должно быть также проведено сравнение экспериментально найденного значения момента инерции для тела заданной формы с соответствующим значением, рассчитанным теоретически.
Контрольные вопросы
Что такое главные оси инерции? Центральные оси? Привести примеры.
Что такое момент инерции тела относительно закрепленной оси?
Чему равны моменты инерции следующих тел: тонкая палочка, тонкий диск, тонкие прямоугольная и треугольная пластины, цилиндр, шар, параллелепипед? Как их получить?
Сформулируйте теорему Гюйгенса-Штейнера.
Литература
Алешкевич В.А., Деденко Л.Г., Караваев В.А. Механика твердого тела. Лекции (Университетский курс общей физики). М.: Изд-во физического факультета МГУ, 1998.
Матвеев А.Н. Механика и теория относительности. 2-е изд. М.: Высшая школа, 1986, § 31,32,34.
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ И ПРОВЕРКА ТЕОРЕМЫ ГЮЙГЕНСА-ШТЕЙНЕРА
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы
Экспериментальная проверка теоремы Гюйгенса – Штейнера и определение моментов инерции тел простой формы.
Идея эксперимента
В эксперименте используется связь между периодом колебаний крутильного маятника и его моментом инерции. В качестве маятника выбрана круглая платформа, подвешенная в поле тяжести на трех длинных нитях (трифилярный подвес). Платформа может совершать крутильные колебания вокруг вертикальной оси. На платформу помещаются тела различной формы, измеряются периоды колебаний маятника и определяются значения моментов инерции этих тел. Теорема Гюйгенса – Штейнера проверяется по соответствию между экспериментальной и теоретической зависимостями моментов инерции грузов от их расстояния до центра платформы.
Теория



Для проверки теоремы Гюйгенса – Штейнера в данной работе исследуются крутильные колебания твердого тела на трифилярном подвесе. Трифилярный подвес представляет собой круглую платформу радиуса R, подвешенную на трех симметрично расположенных нитях одинаковой длины, укрепленных у ее краев (рис. 8). Наверху эти нити также симметрично прикреплены к диску несколько меньшего размера (радиуса r). Платформа может совершать крутильные колебания вокруг вертикальной оси ОО ¢, перпендикулярной к ее плоскости и проходящей через ее центр. Такое движение платформы приводит к изменению положения ее центра тяжести по высоте.
Если платформа массы m, вращаясь в одном направлении, поднялась на высоту h, то
приращение ее потенциальной энергии будет равно

где g – ускорение силы тяжести. Вращаясь в другом направлении, платформа придет в положение равновесия (h = 0) с кинетической энергией, равной

где J – момент инерции платформы, w 0 – угловая скорость вращения платформы в момент прохождения ею положения равновесия.
Пренебрегая работой сил трения, на основании закона сохранения механической энергии имеем:

Считая, что платформа совершает гармонические крутильные колебания, можно записать зависимость углового смещения платформы a от времени t в виде


В моменты прохождения платформы через положение равновесия (t = 0, 0,5Т, …) величина w ( t ) будет максимальна и равна

Из выражений (3.5) и (3.8) следует, что

Если l длина нитей подвеса, R – расстояние от центра платформы до точек крепления нитей на ней, r – радиус верхнего диска (рис. 8), то легко видеть, что

Так как

а при максимальном отклонении платформы от положения равновесия


Измерение времени колебаний может проводиться или с помощью ручного секундомера или с помощью таймера.
Проведение эксперимента
Задание 1. Измерение момента инерции пустой платформы
Дата добавления: 2018-09-22 ; просмотров: 672 ; Мы поможем в написании вашей работы!