что такое вес в геодезии

Веса результатов измерений и их функций

Вес результата измерения определяют по формуле

, (3.11)

где – произвольно выбранное число одинаковое для всех весов, участвующих в решении задачи;

– СКП результата измерения.

Вес – относительная характеристика точности, т.е. он дает представление о точности результата измерения только при сравнении с весами других результатов измерений в данной задаче.

В качестве единицы меры дисперсий принимают СКП измерения , вес которой равен единице (СКП единицы веса).

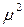
Подставив в (3.11) вместо величину , получим

,

,

. (3.12)

Величину называют обратным весом.

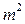
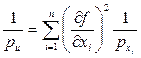
Заменив в формуле (3.6) величины на обратные веса, получаем формулу для вычисления веса функции измеренных величин

. (3.13)

Таким образом, методика определения весов функций измеренных величин такая же, что и при вычислении СКП функций измеренных величин. Формулы для определения весов функций получаются из формул для СКП тех же функций заменой величин соответствующими им обратным весом .

Порядок вычисления веса функции измеренных величин следующий:

1) записывается функция в буквенном выражении;

2) определяется обратный вес этой функции по вышеизложенным правилам;

3) осуществляется переход от обратного веса к весу.

Эта тема принадлежит разделу:

Геодезия

Государственный университет по землеустройству.. кафедра геодезии и геоинформатики..

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Веса результатов измерений и их функций

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Дополнительная
4. Батраков Ю.Г. Геодезические сети специального назначения. М.; Картгеоцентр – Геодезиздат, 1999. 5. Инструкция по развитию съемочного обоснования и съемке ситуации и рельефа с применение

Вычислительная обработка тахеометрического хода
По данным полевого журнала тахеометрической съемки (табл. 2.1.) вычис­лить и занести в журнал для каждой станции среднее значение горизонтального угла, место нуля МО, углы на

Журнал тахеометрической съемки
Станция 216 i = 1,40 м Нст. = Положение вертикального круга № точек наблю-дений Расстояние по дально­меру D’=100

Вычисление координат точек тахеометрического хода
В “Ведомость вычисления координат” из журнала тахеометриче­ской съемки (табл.2.1.) выписать средние значения горизонтальных углов и средние значения горизонтальных проложений сторон

Вычисление высот точек тахеометрического хода
В «Ведомость вычисления высот точек тахеометрического хода» (табл. 2.2.) выписать: – из табл. 1 высоты исходных пунктов

Вычисление высот съемочных пикетов
Из «Ведомости вычисления высот точек тахеометрического хода» (табл. 2.2.) выписать в журнал тахеометрической съемки высоты точек хода. Вычислить последовательно углы наклон

Составление плана участка
На чертежной бумаге размером 3545 см построить координатную сет­ку со сторонами 10 с

Вопросы для самопроверки
1. Какова цель тахеометрической съемки? 2. Как определяют при тахеометрической съемке плановое положение съемочных пикетов и их высоты? 3. В чем различие между абр

Рекомендации по обработке вычислений
Для выполнения контрольной работы по теме «Теория погрешностей измерений» необходимо решить около тридцати контрольных задач. Контрольная работа выполняется в соответствии с вари­антами, у

Решение.
Результаты расчетов сведены в таблицу 3.1 (табличная форма). Табл. 3.1 № п/п Результаты измерений

Задача 1.
Для исследования точности измерения горизонтального угла полным приемом теодолитом 3Т5КП, им был многократно измерен угол. Результаты оказались следующими: 39°17,4′; 39º 16,8′; 39°

Задача 2.
Дана совокупность угловых невязок в треугольниках объемом 50 единиц. На данной совокупности проверить свойства случайных погрешностей. Считая невязки истинными погрешностя­ми, вычислить СКП и про­и

Оценка точности функции измеренных величин
На содержание этого раздела следует обратить особое внимание и учесть порядок определения СКП функции, вычисляемой по измеренным величинам (аргументам) с СКП, связанными с искомой в

Решение.
Для определения погрешности дирекционного угла последней линии, прежде всего, необходимо представить этот дирекционный угол как функцию исходных и измеренных величин. Так как были измерены п

Задача 4.
Линия теодолитного хода измерена частями с СКП

Задача 6.
Вычислить превышение, полученное тригонометрическим нивелированием, и его предельную погрешность, если расстояние, измеренное нитяным дальномером D =210,5м с СКП

Задача 10.
В треугольнике измерены две стороны и

РАВНОТОЧНЫХ ИЗМЕРЕНИЙ
При математической обработке ряда равноточных измерений одной и той же величины вычисляют: 1) среднеарифметическое значение измеренной величи­ны (как наиболее надежное)

Решение.
Дирекционный угол последней линии теодолитного хода вычисляем по известной формуле Условие

Решение.
Длина определяется соотношением

Задача 18.
Чему равен вес среднеарифметического значения угла, полученного из =. приемов (см. приложение табл. 2)?

НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
При математической обработке неравноточных измерений одной и той же величины решаются последовательно следую­щие задачи: 1) определяют средневесовое значение из результатов

Задача 24.
По четырем теодолитным ходам на узловую линию пере­дан дирекционный угол. Число горизонтальных углов поворота в каждом хо­де различно. Произвести математическую обработку результатов значений дирек

Задача 25.
По четырем ходам геометрического нивелирования с различным числом станций была передана высота на узловой репер, что дало результаты (см. приложение табл. 2): № п

Задача 26.
В таблице приведены невязки в полигонах геометрическо­го нивелирования и периметры полигонов. Оценить точность нивелирования. № пол-ов

Задача 27.
Произвести оценку точности измерения горизонтальных углов в замкнутом теодолитном ходе по невязкам в полигонах. № полигонов Число углов в поли

Задача 28.
По невязкам в треугольниках сети триангуляции произвести оценку точности угловых измерений. № треуголь­ников Невязки

Округление приближенных чисел
В приближенных вычислениях часто приходиться округлять числа (как приближенные, так и точные), т. е. отбрасывать одну или несколько последних цифр. Чтобы обеспечить наибольшую близо

Погрешности измерений
Точность измерений характеризуется погрешностями измерений. Погрешностью измерения называют разность между изм

Вопросы для самопроверки
1. Какие измерения называют равноточными? 2. Что называется погрешностью измерений? 3. Как классифицируются погрешности измерений? 4. Какими свойствами обладают случайные

Общая постановка задачи
Если плотность пунктов опорной плановой геодезической сети недостаточна для выполнения топографических съемок, то сеть сгущают путем развития планово-высотного съемочного обосновани

Исходные данные
Схема сети и результаты полевых измерений показаны на рис. 4.1. В соответствии с вариантом индивидуального задания (см. табл. 4 приложения), на схеме изменяют значения длины линии и

Последовательность выполнения работы
Составляют схематический чертеж согласно заданному варианту. Уравнивание углов выполняется в следующем порядке. 4.3.1. Выбирают узловую линию, т.е. линию, примыкающую к узл

Вопросы для самопроверки
1. По какой формуле вычисляется дирекционный угол узловой линии при передаче его от исходной стороны по хо­ду с левыми (правыми) углами? 2. По какой формуле вычисляется окончательное значе

Основные правила дифференцирования
Производная –этопредел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю. Функцию, имеющую конечную производную, называют диффер

Источник

Тема: Элементы теории ошибок измерений.

1. Классификация ошибок измерений

_______ Измерения в геодезии рассматриваются с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей ее точность. Из практики известно, что даже при самой тщательной и аккуратной работе многократные (повторные) измерения не дают одинаковых результатов. Это указывает на то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Значение отклонения характеризует точность измерений.

_______ К грубым ошибкам относятся просчеты в измерениях по причине невнимательности наблюдателя или неисправности прибора, и они полностью должны быть исключены. Это достигается путем повторного измерения.

_______ Систематические ошибки происходят от известного источника, имеют определенный знак и величину и их можно учесть при измерениях и вычислениях.

_______ Случайные ошибки обусловлены разными причинами и полностью исключить их из измерений нельзя. Поэтому возникают две задачи: как из результатов измерений получить наиболее точную величину и как оценить точность полученных результатов измерений. Эти задачи решаются с помощью теории ошибок измерений _______

_______ В основу теории ошибок положены следующие свойства случайных ошибок :
_______ 1. Малые ошибки встречаются чаще, а большие реже.
_______ 2. Ошибки не превышают известного предела.
_______ 3. Положительные и отрицательные ошибки, одинаковые по абсолютной величине, одинаково часто встречаются.
_______ 4. Сумма ошибок, деленная на число измерений, стремится к нулю при большом числе измерений.

_______ По источнику происхождения различают ошибки приборов, внешние и личные. Ошибки приборов обусловлены их несовершенством, например погрешность угла, измеренного теодолитом, неточным приведением в вертикальное положение оси его вращения.

_______ Внешние ошибки происходят из-за влияния внешней среды, в которой протекают измерения, например погрешность в отсчете по нивелирной рейке из-за изменения температуры воздуха на пути светового луча (рефракция) или нагрева нивелира солнечными лучами.

_______ Личные ошибки связаны с особенностями наблюдателя, например, разные наблюдатели по-разному наводят зрительную трубу на визирную цель. Так как грубые погрешности должны быть исключены из результатов измерений, а систематические исключены или ослаблены до минимально допустимого предела, то проектирование измерений с необходимой точностью и оценку результатов выполненных измерений производят, основываясь на свойствах случайных погрешностей.

2. Арифметическая середина

_______ Величина x называется арифметической серединой или вероятнейшим значением измеренной величины. Разности между каждым измерением и арифметической срединой называют вероятнейшими ошибками измерений:

_______ Или в общем виде получим:

3. Средняя квадратическая ошибка

_______ Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле:

где [v 2 ] – сумма квадратов вероятнейших ошибок; n – число измерений. Средняя квадратическая ошибка арифметической середины вычисляется по формуле:

_______ Предельная ошибка не должна превышать утроенной средней квадратической ошибки, т.е. ε = 3 x m.

_______ Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной ошибки. ___

_______ Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины. Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая погрешность измерения линии длиной:

_______ l = 110 м, при m = 2 см, равна m/ l = 1/5500.

_______ Линия измерена шесть раз. Определить ее вероятнейшую длину и оценить точность этого результата. Вычисления приведены в таблице:

Таб. 1

_______ По формулам вычислены абсолютные средние квадратические ошибки, а оценивать точность измерения длины линии необходимо по относительной ошибке. Поэтому нужно абсолютную ошибку разделить на длину линии. Для нашего примера относительная ошибка вероятнейшего значения измеренной линии равна

4. Оценка точности измерений

_______ Точность результатов многократных измерений одной и той же величины оценивают в такой последовательности:

_______ 1. Находят вероятнейшее (наиболее точное для данных условий) значение измеренной величины по формуле арифметической середины х = [ l ]/n.
_______ 2. Вычисляют отклонения для каждого значения измеренной величины от значения арифметической средины. Контроль вычислений: [v] = 0;
_______ 3. По формуле вычисляют среднюю квадратическую ошибку одного измерения.
_______ 4. По формуле вычисляют среднюю квадратическую ошибку арифметической средины.
_______ 5. Если измеряют линейную величину, то подсчитывают относительную среднюю квадратическую ошибку каждого измерения и арифметической средины.

_______ 6. При необходимости подсчитывают предельную ошибку одного измерения, которая может служить допустимым значением погрешностей аналогичных измерений.

5. Понятие о неравноточных измерениях

_______ Неравноточными измерениями называются такие, которые выполнены различным числом приемов, приборами различной точности и т.д. Если измерения неодинаковой точности, то для определения общей арифметической середины пользуются формулой:

________ Весом называется число, которое выражает степень доверия к результату измерения. В тех случаях, когда неизвестны веса измеренных величин, а известны их средние квадратические ошибки, то веса можно вычислить по формуле:

т.е. вес результата измерений обратно пропорционален квадрату средней квадратической ошибки.

_______ При неравноточных измерениях средняя квадратическая ошибка измерения, вес которого равен единице, определяется по формуле:

где δ – разность между отдельными результатами измерений и общей арифметической серединой.

Источник

Геодезические измерения

3.1 В повседневной деятельности постоянно приходится сталкиваться с необходимостью измерений. В случае «штучности» объектов достаточно простого счёта, иначе необходимо сравнение с некоторыми заранее определёнными величинами. Такой процесс сравнения называют измерением. Результат измерения – число; таким образом объект получает количественную характеристику.

Прямые и косвенные методы измерений. Измерение – это процесс сравнения измеряемой величины и некоторой заранее определённой. Измерения бывают прямыми – когда измеряется непосредственно величина, и косвенные – когда измеряются некоторые величины, от которых искомая зависит функционально. Так, при измерении расстояния рулеткой используют прямой метод, при измерении площади – косвенный.

Для ослабления влияния систематических погрешностей применяют: введение поправок (равных погрешности по модулю и противоположных по знаку); выбор методики измерений (погрешности входят в результаты измерений с противоположными знаками, что освобождает от их влияния среднее арифметическое); ограничивают условия измерений (минимизируют величину систематической погрешности). Случайной погрешностью называют такую погрешность, величину и знак которой до проведения эксперимента (измерения) невозможно предсказать. Случайные погрешности обладают рядом свойств (не превышают предельной погрешности, отклонения, равные по величине и противоположные по знаку – равновероятны, малые отклонения встречаются чаще больших), из которых вытекает, что среднее арифметическое случайных погрешностей стремится к нулю. Если имеется ряд результатов измерений одной и той же величины, то необходимо определить наиболее надёжное значение. За такое значение принимают арифметическую средину (среднее арифметическое). Среднее арифметическое является экспериментальной оценкой математического ожидания, поэтому среднее арифметическое называют вероятнейшим значением.

3.3 Точность измерений. Погрешности функций измеренных величин. Оценки точности измерений. Точность измерений выражает степень близости результата измерения к действительному значению. Из-за наличия случайных погрешностей эта близость различна для разных результатов. Если одну и ту же величину измеряют одним и тем же способом при одних и тех же условиях, то результаты таких измерений называются равноточными. Точность измерений выражает степень близости результата измерений к действительному значению величины. Точность измерений характеризуют средней величиной случайной погрешности (случайного отклонения от истинного значения). В качестве теоретической характеристики берут среднее квадратическое отклонение

где D – дисперсия случайной погрешности измерения Δ. Так как величина σ – чисто теоретическая, то обычно пользуются средней квадратической погрешностью, или эмпирическим средним квадратическим отклонением, которое определяется по формуле

где Δ_i = l_i – Х – истинная погрешность i-того измерения. В случае, если не известно Х, используют отклонение результатов измерений l_i от вероятнейшего значения Х₀:

m = √(Σν_i 2 /(n – 1)) (формула Бесселя),

где ν_i = l_i – Х₀. При большом количестве измерений среднеквадратическая погрешность и квадратическое отклонение практически равны. Если известны средние квадратические погрешности некоторых величин, то можно определить среднеквадратическую погрешность функции от них. Если определена функция измеренных величин Φ = φ (x, y, …, z) и известны погрешности аргументов m_x, m_y, m_z, то квадрат средней квадратической погрешности функции вычисляют по формуле

Пусть имеется ряд измерений одной величины: l₁, l₂, …, l_n. Если средние квадратические погрешности этих измерений равны: m₁ = m₂ = … = m_n, то такой ряд называют равноточным. Таковыми будут, например, измерения, проведенные по одной методике одним и тем же прибором наблюдателями одинаковой квалификации. Если хотя бы одна из величин имеет среднюю квадратическую погрешность, отличную от других, то такой ряд называют неравноточным. Такое может произойти, если некоторые из ряда измерений производились прибором одной точности, а остальные – прибором другой точности. Для определения вероятнейшего значения и оценки точности используется понятие о весе. Вес результата измерения – это численная характеристика доверия к этому измерению. Вес p_i в общем виде характеризуют следующим отношением: p_i = c/m 2 _i, где с – постоянное для данного рада положительное число. Отметим, что от выбора численного значения величины «с» окончательный результат (вероятнейшее значение) и оценка его точности не зависят. Если даны результаты неравноточных измерений l₁, l₂, …, l_n и их веса p₁, p₂, …, p_n, то вероятнейшее значение вычисляют по формуле

Для оценки точности вычисляют среднюю квадратическую погрешность измерения с весом p_i = 1. Эту погрешность называют погрешностью единицы веса и вычисляют по формуле

где δ_i = l_i – Х₀ – отклонение от вероятнейшего значения (весового среднего). Для оценки точности Х и результатов измерений используют формулы

Для назначения весов не обязательно знать средние квадратические погрешности измерений. Обычно используют косвенные характеристики.

Одной из важных задач теории погрешностей является вычисление допустимых невязок и расхождений при проведении геодезических работ. Отправной точкой для расчётов допусков служит то, что невязка является погрешностью самой невязки. Так как погрешность – разность между результатом измерения и его точным значением, то Δf = f – f_т = f, где Δf – погрешность невязки. Следовательно, предельно возможное значение невязки (допустимая невязка), совпадает с предельной погрешностью этой невязки (f_доп = Δf_пред). Предельную погрешность Δf_пред можно вычислить, если известна средняя квадратическая погрешность невязки m_f; тогда Δf_пред = τm_f, где τ может принимать значения 2, 2,5, 3 в зависимости от условий. Значение m_f может быть вычислено по известным правилам оценки точности функций в зависимости от вида геодезических операций.

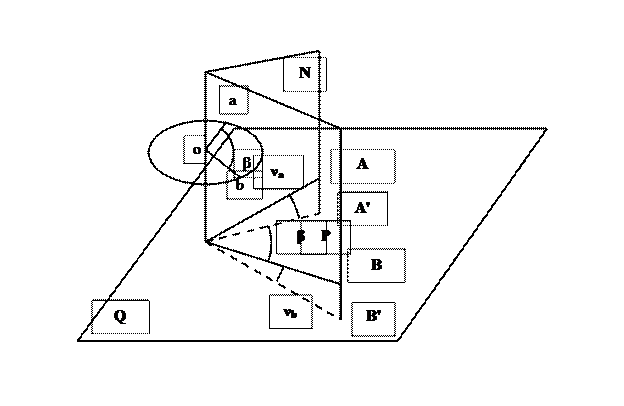
Угловые измерения

Рис. 9. Измерение горизонтальных и вертикальных углов.

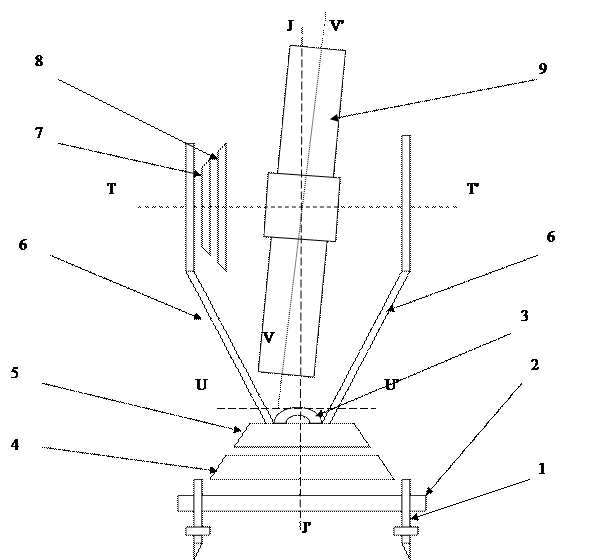
3.5 Приборы для измерения углов. Описанный метод измерения углов реализован в теодолите. Основными частями теодолита являются горизонтальный и вертикальный круги, зрительная труба, цилиндрический уровень, подъёмные винты, винты закрепительные (алидад вертикального и горизонтального кругов и лимба горизонтального круга) и наводящие винты алидад вертикального и горизонтального кругов, а также лимба горизонтального круга. В принципиальной схеме теодолита выделяют четыре основных оси: вертикальную ось JJ’, ось цилиндрического уровня UU’, визирную ось VV’ и ось вращения зрительной трубы TT’ (рис. 10).

Рис. 10. Принципиальная схема теодолита.

На схеме условно обозначены: 1. подъёмные винты; 2. трегер; 3. цилиндрический уровень горизонтального круга; 4. лимб горизонтального круга; 5. алидада горизонтального круга; 6. колонка; 7. алидада вертикального круга; 8. лимб вертикального круга; 9. зрительная труба.

Рис. 11. Оптический теодолит 4Т15П. Увеличение зрительной трубы 20˟, средняя квадратическая погрешность измерения одним приёмом: вертикального угла – 15˝, горизонтального угла – 15˝.

3.6 Поверки и юстировки оптических теодолитов. Основные геометрические условия, которые должны быть соблюдены в теодолите, вытекают из принципиальной схемы измерения горизонтального угла и заключаются в следующем: 1. вертикальная ось (ось вращения алидады) инструмента должна быть отвесна, 2. плоскость лимба должна быть горизонтальна, 3. визирная плоскость должна быть вертикальна.

Для выполнения этих условий выполняются следующие поверки теодолита.

1. Ось цилиндрического уровня UU΄ при алидаде горизонтального круга должна быть перпендикулярна к вертикальной оси JJ΄ прибора.

2. Визирная ось зрительной трубы VV΄ должна быть перпендикулярна к горизонтальной оси TT΄ теодолита.

3. Горизонтальная ось вращения трубы TT΄ должна быть перпендикулярна к вертикальной оси JJ΄ прибора.

4. Одна из нитей сетки должна быть параллельна, другая перпендикулярна к вертикальной оси теодолита.

Первая поверка выполняется следующим образом. Пусть ось уровня не перпендикулярна вертикальной оси прибора и составляет с ним угол α. Тогда при повороте алидады на 180˚ угол также составит α, но при этом ось будет наклонена в другую сторону. Разность отсчётов по уровню даст величину 2α. Т.о., ось уровня необходимо наклонить на половину угла, равного разности отсчётов. На практике поверку выполняют так: пузырёк уровня, установленного параллельно двум подъёмным винтам, приводят в нуль-пункт. Сняв отсчёт по горизонтальному кругу, поворачивают алидаду на 180˚. При отклонении пузырька от середины ампулы выполняется юстировка: исправительными винтами его перемещают на половину отклонения; на вторую половину – подъёмными винтами. После этого поверку повторяют[1].

Угол отклонения визирной оси зрительной трубы от перпендикуляра к горизонтальной оси прибора называют коллимационной погрешностью. Для её определения наводят теодолит на удалённую точку и снимают отсчёт А при, скажем, круге право (КП). Переводят трубу через зенит и снова визируют эту точку при круге лево (КЛ), получая отсчёт В. Тогда при отсутствии погрешности В – А = ± 180˚. Если погрешность есть, то отсчёт при круге право будет отличаться от истинного отсчёта R на некоторую величину с: R=А+с. Очевидно, что для круга лево R=В – с ± 180˚, т.к. визирная ось отклонится в противоположную сторону. Т.о., среднее из отсчётов свободно от влияния коллимационной погрешности, а сама погрешность может быть найдена по формуле с = (В – А ± 180˚)/2. Для исключения коллимационной погрешности (в случае, если она превышает удвоенную точность отсчётного устройства) устанавливают на лимбе средний отсчёт; тогда центр сетки нитей сойдёт с визируемой точки. Исправительными винтами сетки совмещают её центр с визируемой точкой. Поверку повторяют.

Для проверки выполнения третьего условия теодолит устанавливают на расстоянии около 4-6 метров от какой-либо стены и, наведя перекрестие сетки нитей на точку М, при закрепленной алидаде опускают зрительную трубу до горизонтального положения визирной оси и отмечают на стене проекцию перекрестия сетки нитей. Переведя трубу через зенит, снова аналогичным способом проецируют ту же точку М. При совпадении точек условие выполнено. При несоблюдении данного условия устранение погрешности, вызванное неравенством колонок, возможно только в мастерской[2], так как в современных приборах отсутствуют исправительные винты подставок приборов.

Последнюю поверку выполняют одним из следующих способов. Центр сетки наводят на какую-либо точку и поворачивают трубу наводящим винтом алидады. Если при этом точка не сходит с горизонтальной нити, то условие выполнено. Иначе: на небольшом от прибора расстоянии (в безветренную погоду) подвешивают отвес и наводят на него вертикальную нить, которая должна совпадать с линией отвеса. В случае, если условие не выполнено, то, открепив юстировочные винты сетки нитей, следует повернуть её на необходимый угол. После закрепления винтов сетки нитей необходимо повторить вторую поверку.

Дата добавления: 2015-12-26 ; просмотров: 3035 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник