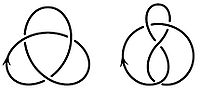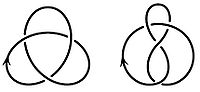Что такое узлы в математике
Математический узел
Содержание
Понятие математического узла
Узлы — предметы простые и наглядные. Вы, конечно, встречались с ними в повседневной жизни, но, может быть, не подозревали, что это ещё и математические объекты; более того, в последние 20 лет математики и физики с огромным интересом и удивительной интенсивностью стали заниматься соответствующими теориями, особенно теорией узлов. Достаточно сказать, что за это время четыре медали Филдса были получены именно за работы, связанные с этой теорией. А именно, лауреатами медали Филдса в разное время стали Владимир Дринфельд из Харькова, работающий в Чикаго, Максим Концевич из Москвы, работающий в Париже, Воган Джонс из Новой Зеландии, работающий в Калифорнии, и Эдвард Виттен, физик-теоретик, работающий в Принстоне.
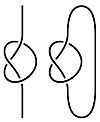
Чем отличается математический узел от узлов, которые завязывают на галстуках или на шнурках ботинок? Естественно, в математике узел — это некая абстракция: рассматривается не верёвка и не шнур, а бесконечно тонкая, гибкая и растяжимая нить. Кроме того, рассматривая математический узел, нужно либо как-то зафиксировать его концы (обычно говорят, что один конец уходит в бесконечность «вверх», а другой — в бесконечность «вниз», либо просто соединить их (см. рис.). В последнем случае модель узла — замкнутая несамопересекающаяся кривая в пространстве. Будем предполагать, что эта кривая является ломаной, то есть состоит из отрезков (впрочем, на рисунках мы почти всегда будем изображать узлы в виде гладких кривых, считая отдельные звенья ломаной. Самый простой узел — тривиальный (простая окружность). Узел называется нетривиальным, если он не эквивалентен тривиальному, то есть его нельзя «пошевелить» (возможно растягивая, но не разрывая верёвку) так, чтобы он превратился в тривиальный.
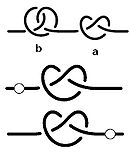
Вот несколько примеров нетривиальных узлов: узел на рис. слева называется трилистником, узел на рис. справа — восьмёркой. (Обычно узлы рассматривают с ориентацией, то есть считают, что задано направление обхода кривой, это направление изображается стрелкой.)
Алгебра узлов
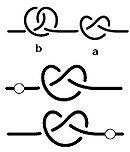
А можно ли умножать узлы? Если считать узлы кривыми, концы которых уходят в бесконечность, то умножение узлов определяется естественным образом: произведение узлов а и b — это просто нить, на которой завязан сначала узел а, затем узел b (рис. справа). Это умножение ассоциативно: для любых узлов а, b и с верно равенство: (ab)c=a(bc). Ясно, что тривиальный узел (то есть просто вертикальная прямая) является единичным элементом. Ни один нетривиальный узел не имеет обратного. Покажем, что два узла, завязанные на одной веревке, можно переставить. Действительно, пусть на нити завязан сначала узел a, затем узел b. Сперва, не трогая узел a, «затянем» узел b в маленький узелок. Потом заключим этот узелок в маленький стеклянный шарик и будем двигать его вверх по нити. В итоге этот шарик окажется наверху, и его можно превратить опять в узел b. Таким образом, умножние узлов коммутативно: ab=ba.
Итак, верна
Теорема об узлах. Узлы образуют ассоциативную и коммутативную систему относительно умножения. В этой системе есть единичный элемент, но нет обратных.
Компьютер развязывает узлы
Первый шаг в этой теории состоит в сведении (сложной) пространственной задачи развязывания узла к (более простой) задаче применения простых операций к кривым на плоскости. Эти операции придумал в 1920-е годы немецкий математик Рейдемейстер.
Имеет место
Лемма Рейдемейстера. Если узел можно развязать (превратить в окружность) в пространстве, то его плоскую диаграмму можно распутать на плоскости с помощью операций Рейдемейстера.
Узел (математика)
Содержание
Понятие математического узла
Узлы — предметы простые и наглядные. Вы, конечно, встречались с ними в повседневной жизни, но, может быть, не подозревали, что это ещё и математические объекты; более того, в последние 20 лет математики и физики с огромным интересом и удивительной интенсивностью стали заниматься соответствующими теориями, особенно теорией узлов. Достаточно сказать, что за это время четыре медали Филдса были получены именно за работы, связанные с этой теорией. А именно, лауреатами медали Филдса в разное время стали Владимир Дринфельд из Харькова, работающий в Чикаго, Максим Концевич из Москвы, работающий в Париже, Воган Джонс из Новой Зеландии, работающий в Калифорнии, и Эдвард Виттен, физик-теоретик, работающий в Принстоне.
Чем отличается математический узел от узлов, которые завязывают на галстуках или на шнурках ботинок? Естественно, в математике узел — это некая абстракция: рассматривается не верёвка и не шнур, а бесконечно тонкая, гибкая и растяжимая нить. Кроме того, рассматривая математический узел, нужно либо как-то зафиксировать его концы (обычно говорят, что один конец уходит в бесконечность «вверх», а другой — в бесконечность «вниз», либо просто соединить их (см. рис.). В последнем случае модель узла — замкнутая несамопересекающаяся кривая в пространстве. Будем предполагать, что эта кривая является ломаной, то есть состоит из отрезков (впрочем, на рисунках мы почти всегда будем изображать узлы в виде гладких кривых, считая отдельные звенья ломаной. Самый простой узел — тривиальный (простая окружность). Узел называется нетривиальным, если он не эквивалентен тривиальному, то есть его нельзя «пошевелить» (возможно растягивая, но не разрывая верёвку) так, чтобы он превратился в тривиальный.
Вот несколько примеров нетривиальных узлов: узел на рис. слева называется трилистником, узел на рис. справа — восьмёркой. (Обычно узлы рассматривают с ориентацией, то есть считают, что задано направление обхода кривой, это направление изображается стрелкой.)
Группа узлов
Если считать узлы кривыми, концы которых уходят в бесконечность, то умножение узлов определяется естественным образом: произведение узлов а и b — это просто нить, на которой завязан сначала узел а, затем узел b (рис. справа). Это умножение ассоциативно: для любых узлов а, b и с верно равенство: (ab)c=a(bc). Ясно, что тривиальный узел (то есть просто вертикальная прямая) является единичным элементом. Ни один нетривиальный узел не имеет обратного. Покажем, что два узла, завязанные на одной веревке, можно переставить. Действительно, пусть на нити завязан сначала узел a, затем узел b. Сперва, не трогая узел a, «затянем» узел b в маленький узелок. Потом заключим этот узелок в маленький стеклянный шарик и будем двигать его вверх по нити. В итоге этот шарик окажется наверху, и его можно превратить опять в узел b. Таким образом, умножние узлов коммутативно: ab=ba.
Итак, верна
Теорема об узлах. Узлы образуют ассоциативную и коммутативную систему относительно умножения.
В этой системе есть единичный элемент, но нет обратных.
Компьютер развязывает узлы
Первый шаг в этой теории состоит в сведении (сложной) пространственной задачи развязывания узла к (более простой) задаче применения простых операций к кривым на плоскости. Эти операции придумал в 1920-е годы немецкий математик Рейдемейстер.
Имеет место
Лемма Рейдемейстера. Если узел можно развязать (превратить в окружность) в пространстве, то его плоскую диаграмму можно распутать на плоскости с помощью операций Рейдемейстера.
Статья по математике на тему: «Понятия узлов»(11 класс)
Научный руководитель Кухарева И.М.
Понятие математического узла
Трилистник и восьмёрка
А можно ли умножать узлы? Если считать узлы кривыми, концы которых уходят в бесконечность, тоумножение узлов определяется естественным образом: произведение узлов а и b — это просто нить, накоторой завязан сначала узел а, затем узел b (рис. справа). Это умножение ассоциативно: для любых узлов а,b и с верно равенство: (ab)c=a(bc). Ясно, что тривиальный узел (то есть просто вертикальная прямая)является единичным элементом. Ни один нетривиальный узел не имеет обратного. Покажем, что два узла,завязанные на одной веревке, можно переставить. Действительно, пусть на нити завязан сначала узел a,затем узел b. Сперва, не трогая узел a, «затянем» узел b в маленький узелок. Потом заключим этот узелок вмаленький стеклянный шарик и будем двигать его вверх по нити. В итоге этот шарик окажется наверху, и егоможно превратить опять в узел b. Таким образом, умножние узлов коммутативно: ab=ba.
Итак, верна
Теорема об узлах. Узлы образуют ассоциативную и коммутативную систему относительно умножения. В этойсистеме есть единичный элемент, но нет обратных.
Компьютер развязывает узлы
Журнал GEO непознанный мир: земля №01(166) январь 2012
Узел (топология)
Содержание
Понятие математического узла
Узлы — предметы простые и наглядные. Вы, конечно, встречались с ними в повседневной жизни, но, может быть, не подозревали, что это ещё и математические объекты; более того, в последние 20 лет математики и физики с огромным интересом и удивительной интенсивностью стали заниматься соответствующими теориями, особенно теорией узлов. Достаточно сказать, что за это время четыре медали Филдса были получены именно за работы, связанные с этой теорией. А именно, лауреатами медали Филдса в разное время стали Владимир Дринфельд из Харькова, работающий в Чикаго, Максим Концевич из Москвы, работающий в Париже, Воган Джонс из Новой Зеландии, работающий в Калифорнии, и Эдвард Виттен, физик-теоретик, работающий в Принстоне.
Чем отличается математический узел от узлов, которые завязывают на галстуках или на шнурках ботинок? Естественно, в математике узел — это некая абстракция: рассматривается не верёвка и не шнур, а бесконечно тонкая, гибкая и растяжимая нить. Кроме того, рассматривая математический узел, нужно либо как-то зафиксировать его концы (обычно говорят, что один конец уходит в бесконечность «вверх», а другой — в бесконечность «вниз», либо просто соединить их (см. рис.). В последнем случае модель узла — замкнутая несамопересекающаяся кривая в пространстве. Будем предполагать, что эта кривая является ломаной, то есть состоит из отрезков (впрочем, на рисунках мы почти всегда будем изображать узлы в виде гладких кривых, считая отдельные звенья ломаной. Самый простой узел — тривиальный (простая окружность). Узел называется нетривиальным, если он не эквивалентен тривиальному, то есть его нельзя «пошевелить» (возможно растягивая, но не разрывая верёвку) так, чтобы он превратился в тривиальный.
Вот несколько примеров нетривиальных узлов: узел на рис. слева называется трилистником, узел на рис. справа — восьмёркой. (Обычно узлы рассматривают с ориентацией, то есть считают, что задано направление обхода кривой, это направление изображается стрелкой.)
Алгебра узлов
А можно ли умножать узлы? Если считать узлы кривыми, концы которых уходят в бесконечность, то умножение узлов определяется естественным образом: произведение узлов а и b — это просто нить, на которой завязан сначала узел а, затем узел b (рис. справа). Это умножение ассоциативно: для любых узлов а, b и с верно равенство: (ab)c=a(bc). Ясно, что тривиальный узел (то есть просто вертикальная прямая) является единичным элементом. Ни один нетривиальный узел не имеет обратного. Покажем, что два узла, завязанные на одной веревке, можно переставить. Действительно, пусть на нити завязан сначала узел a, затем узел b. Сперва, не трогая узел a, «затянем» узел b в маленький узелок. Потом заключим этот узелок в маленький стеклянный шарик и будем двигать его вверх по нити. В итоге этот шарик окажется наверху, и его можно превратить опять в узел b. Таким образом, умножние узлов коммутативно: ab=ba.
Итак, верна
Теорема об узлах. Узлы образуют ассоциативную и коммутативную систему относительно умножения. В этой системе есть единичный элемент, но нет обратных.
Компьютер развязывает узлы
Первый шаг в этой теории состоит в сведении (сложной) пространственной задачи развязывания узла к (более простой) задаче применения простых операций к кривым на плоскости. Эти операции придумал в 1920-е годы немецкий математик Рейдемейстер.
Имеет место
Лемма Рейдемейстера. Если узел можно развязать (превратить в окружность) в пространстве, то его плоскую диаграмму можно распутать на плоскости с помощью операций Рейдемейстера.
Что такое узлы в математике
Узел — метод для соединения и защиты линейного материала, типа верёвки при помощи связывания и переплетения. Он может включать один или более кусков верёвки, струны, тесьмы, бечёвки, ремня и других деталей, сплетённых в цепь так, что они соединены между собой и/или с объектом-грузом. Узлы интересны своим древним происхождением, своими практическими применениями, а также теорией узлов — областью математики, исследующей их свойства.
Содержание
Классификация
По назначению
Выделяют декоративное назначение узлов: существует отдельная классификация галстучных узлов, например, узел «полный виндзор».
По разъёмности
По надёжности
Некоторые узлы склонны к саморазвязыванию, либо портят верёвку. Во времена парусного флота считалось, что простой узел снижает надёжность верёвки в 2 раза; прямой узел достаточно надёжен только при увязывании поклажи, а для связывания двух верёвок ни моряки, ни альпинисты его не используют. А похожий на него и часто завязываемый неумелыми людьми бабий очень легко скользит и развязывается. И Прямой и Бабий узлы унесли не одну человеческую жизнь.
По использованию компонентов верёвки
Компоненты
См. также
Литература
Ссылки
Полезное
Смотреть что такое «Узел» в других словарях:
УЗЕЛ — (Knot) 1. Всякая схватка или петля, сделанная на снасти или вокруг чего либо; связка концов тросов между собой. У. бабий (Grannies knot, carrick bend) неправильно завязанный прямой или рифовый У. У. беседочный (Bowline hitch) надежный,… … Морской словарь
УЗЕЛ — (1) УЗЕЛ (1) узла, м. 1. Место, где связаны концы чего н. (веревок, канатов, ниток), или завитое в петлю и стянутое место на веревке, канате, нитке. Завязать узлом. Завязать узел. Узлы на веревке. Морской узел. Глухой узел. 2. перен. Место… … Толковый словарь Ушакова
УЗЕЛ — (1) УЗЕЛ (1) узла, м. 1. Место, где связаны концы чего н. (веревок, канатов, ниток), или завитое в петлю и стянутое место на веревке, канате, нитке. Завязать узлом. Завязать узел. Узлы на веревке. Морской узел. Глухой узел. 2. перен. Место… … Толковый словарь Ушакова
УЗЕЛ — муж. (узкий) узловина муж. (а пск., жен.) узляк, ка муж., курск. узол, вост. узелок, лочек, узлишка узлища,; перевой гибких концов и затяжка их, завязка. Узлы вяжутся различным перевоем; в домашнем обиходе знают: глухой, бабий или простой узел;… … Толковый словарь Даля
УЗЕЛ — • УЗЕЛ, 1). В анатомии утолщение или увеличение органа или ткани, например лимфатический узел или синусно предсердный узел нервной ткани, контролирующий ритм сердца. 2). В ботанике узел место на стебле растения, откуда отходит лист или листья. 3) … Научно-технический энциклопедический словарь
узел — См. связка в узел завязать, разрубать гордиев узел, рассечь гордиев узел. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. узел связка; блок, прибор, установка, агрегат, секция,… … Словарь синонимов
узел — 1. УЗЕЛ, узла; м. 1. Затянутая петля на верёвке, канате и т.п.; место, где связаны концы чего л. (верёвки, нитки, платка и т.п.). Большой, тугой, сложный у. Верёвочный у. У. на галстуке. Завязать узлом. Развязать у. Затянуть у. Распутывать узлы… … Энциклопедический словарь
узел — узел логический узел Точка присоединения к сети, устройство, подключенное к сети (компьютер, мост, маршрутизатор, порт коммутатора, шлюз и т.п.). В общем случае может использоваться для обозначения любого активного элемента сети. Синоним понятия… … Справочник технического переводчика
Узел — – область сопряжения двух или более элементов конструкции. При расчете узлом считается группа всех основных элементов, необходимых для представления работы узла в процессе передачи соответствующих внутренних сил и моментов. Узел сопряжения… … Энциклопедия терминов, определений и пояснений строительных материалов
Узел — морской: а беседочный; б шкотовый; в выбленочный; г восьмёрка; д удавка; е плоский; ж шлюпочный; з кошачьи лапки; и рыбацкий штык; к стопорный; л штык с двумя шлагами. УЗЕЛ, 1) место соединения двух тросов или петля (схватка), стянутая на тросе.… … Иллюстрированный энциклопедический словарь
УЗЕЛ — в технике 1) Часть машины, механизма, установки и т. п.; состоящая из нескольких более простых элементов (деталей)2)] Совокупность функционально связанных сооружений, машин или других устройств (напр., гидроузел, радиоузел)3) Пункт на пересечении … Большой Энциклопедический словарь