Что такое условная гибкость

Что такое жесткость и гибкость элементов

Разницу в работе гибких и жестких стержней под воздействием нагрузки люди заметили достаточно давно. Так один из мастеров восточных единоборств, гуляя по зимнему саду, сделал примерно следующий вывод: жесткая сухая ветка под тяжестью налипшего снега ломается, а гибкая ветка прогибается и, сбросив налипший снег, возвращается в прежнее положение с минимумом повреждений.

Если перевести это гибкую поэтическую аллегорию, помогавшую мастеру восточных единоборств привлекать новых учеников, на современный жесткий язык теории сопротивления материалов, то звучать это будет примерно так: если напряжения в рассматриваемом поперечном сечении жесткого элемента конструкции превышают значение нормативного сопротивления, то это приведет сначала к значительным пластическим деформациям, а затем, при увеличении напряжений, и к разрушению жесткого элемента (будет это разрушение хрупким или вязким, принципиального значения не имеет). В то же время гибкий элемент конструкции под действием такой же нагрузки, не разрушится, но потеряет устойчивость.

Конечно же мне, как и любому другому обычному человеку, гораздо ближе и понятнее определение жесткости и гибкости, данное средневековым мастером восточных единоборств. Но справедливости ради следует отметить, что этот мастер сильно перегнул палку (точнее ветку или, выражаясь языком строительной механики, стержень). Дело в том, что гибкий стержень потеряет устойчивость задолго до того, как значение нагрузки в переводе на напряжения в рассматриваемом сечении достигнет уровня нормативного сопротивления.

Чтобы было более понятно, о чем идет речь, приведу еще один пример.

Если взять достаточно ровный человеческий волос со среднестатистического человека длиной 10 см и попробовать его разорвать руками, то это будет не так уж и просто, для этого следует приложить достаточно большую физическую силу, или выражаясь по-научному, создать достаточно большие растягивающие напряжения в волосе или растягивающую силу около 5 кг (может больше, может меньше, не в этом суть).

А вот если мы попробуем поставить этот волос в вертикальное положение, например, на стол, то волос стоять не будет, а будет сгибаться под действием своего собственного веса, вряд ли превышающего несколько миллиграмм, даже если мы обеспечим ему такое закрепление на верхней опоре, при котором верх волоса не сможет смещаться в горизонтальном направлении, но сможет смещаться в вертикальном направлении.

Вот такое, условно говоря, сгибание и означает потерю устойчивости. Таким образом использовать очень гибкие стержни в качестве сжатых элементов строительных конструкций не имеет никакого смысла.

Между тем, если мы отрежем от этого же волоса кусок длиной 1 см, то этот кусок уже будет сгибаться не так сильно под действием собственного веса и будет обладать некоторой устойчивостью, а если это будет волос длиной 2-5 мм, то об него уже можно сильно уколоться, а волос при этом даже и не согнется.

Как, надеюсь, понятно из вышеприведенного примера, даже для стержня с постоянными геометрическими характеристиками поперечного сечения (радиусом инерции и моментом инерции) его устойчивость зависит от расчетной длины стержня. Другими словами один и тот же стержень может быть и гибким и жестким в зависимости от его расчетной длины.

Для того, чтобы определить гибкость элемента, достаточно расчетную длину элемента l_o разделить на радиус инерции i поперечного сечения (при условии, что параметры поперечных сечений постоянны по всей длине элемента):

Примечание: в различных нормативных документах указанные характеристики могут иметь и другие обозначения, но принципиального значения это не имеет.

Таким образом чем меньше гибкость элемента, тем он более жесткий, соответственно чем больше гибкость элемента, тем более он гибкий. А чтобы определить, не является ли такая гибкость чрезмерной для рассматриваемого элемента конструкции, используются таблицы из соответствующих нормативных документов.

Например, при расчете сжатых элементов стальных конструкций используется такая таблица:

Таблица 19* (согласно СНиП II-23-81 (1990))

А при расчете деревянных конструкций, такая:

Таблица 251.1. Предельные значения гибкости (согласно СНиП II-25-80 (1988))

На значение гибкости влияет и модуль упругости материала. Чем меньше значение модуля упругости, тем больше может быть гибкость. В связи с этим предельно допустимые значения гибкости могут быть разные для элементов из различных материалов, что и отражено в указанных таблицах.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

В каких случаях не требуется проверки общей устойчивости изгибаемого элемента?

-при передаче нагрузки через сплошной жесткий настил, непре-

рывно опирающийся на сжатый пояс балки и надежно с ним связанный

(железобетонные плиты, плоский и профилированный металлический на-

стил, волнистая сталь и т.п.);

Для каких стержней характерна потеря устойчивости?

При достижении какой силы прямолинейная форма стержня перестает быть устойчивой?

При достижении силой критического значения

Запишите формулу Л. Эйлера.

где E – модуль упругости; Imin – минимальный осевой момент инерции;

lef – расчетная длина стержня, зависящая от условий закреплений.

Запишите формулу критических напряжений.

Для каких деформаций справедлива формула Л. Эйлера?

В пределах упругих деформаций

За счет чего может быть увеличена несущая способность стержня?

путем увеличения момента инерции, без изменения площади поперечного сечения, путем размещения материала как можно дальше от главных осей инерции поперечного сечения.

С какой целью центрируется нагрузка сжатого стержня?

Связь между прогибом и нагрузкой зависит в значительной степени от точности, с какой центрирована нагрузка

Когда стержень считается жестким, а когда гибким?

Запишите условие обеспечения устойчивости гибкого стержня.

где А – площадь сечения; j – определяется по [1] в зависимости от условной гибкости l.

Как определяется условная гибкость стержня?

где l – гибкость, то есть l = lef / i; E – модуль упругости; – радиус инерции; lef – расчетная длина стержня; А – площадь сечения; I – осевой момент инерции.

29. Каким известным соотношением можно записать коэффициент ?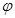

Для стержней со сплошной стенкой значения условной гибкости l при вычислении коэффициента j по формулам из [1] определяется в трех случаях:

От каких условий зависит расчетная длина сжатого стержня (стойки)?

Расчетная длина стержня зависит от условий его закрепления и определяется по формуле lef = lc m

где lc – длина стойки; m – коэффициент приведения к расчетной длине, зависящий от способов закрепления стержня, например, с шарнирно опертыми концами стойки m = 1.

Сварные соединения

В чем заключается физический процесс сварки?

Процесс сварки состоит в молекулярной диффузии металлов свариваемых изделий и плавящегося электрода, находящихся в жидком или высокопластичном состоянии и в совместной кристаллизации металлов при остывании.

2. Перечислите зоны сварного соединения.

зона расплавления, зона термического влияния, весь остальной металл изделия

Дайте определение зоны термического влияния (ЗТВ).

Прилегающий к шву участок основного металла, нагретого выше температуры 723 °С и ниже температуры расплавления 1535 °С называется зоной термического влияния

Источник

СНиП II-23-81 => Таблица 18. Предельные гибкости сжатых элементов. Таблица 19*. Предельные гибкости растянутых элементов. Таблица 20*.

6.11*. Коэффициенты расчетной длины m отдельных участков ступенчатых колонн в плоскости рамы следует определять согласно прил. 6.

При определении коэффициентов расчетной длины m и для ступенчатых колонн рам одноэтажных производственных зданий разрешается:

не учитывать влияние степени нагружения и жесткости соседних колонн;

определять расчетные длины колонн лишь для комбинации нагрузок, дающей наибольшие значения продольных сил на отдельных участках колонн, и получаемые значения m использовать для других комбинаций нагрузок;

для многопролетных рам (с числом пролетов два и более) при наличии жесткого диска покрытия или продольных связей, связывающих поверху все колонны и обеспечивающих пространственную работу сооружения, определять расчетные длины колонн как для стоек, неподвижно закрепленных на уровне ригелей;

для одноступенчатых колонн при соблюдении условий l₂/l₁ £ 0,6 и N₁/N₂ ³ 3 принимать значения m по табл. 18.

Таблица 18

Условия закрепления верхнего конца колонны

Коэффициенты m для участка колонны

Конец, закрепленный только от поворота

Неподвижный, шарнирно опертый конец

Неподвижный, закрепленный от поворота конец

Обозначения, принятые в таблице 18:

6.13. Расчетные длины колонн в направлении вдоль здания (из плоскости рам) следует принимать равными расстояниям между закрепленными от смещения из плоскости рамы точками(опорами колонн, подкрановых балок и подстропильных ферм; узлами креплений связей и ригелей и т. п.). Расчетные длины допускается определять на основе расчетной схемы, учитывающей фактические условия закрепления концов колонн.

6.14. Расчетную длину ветвей плоских опор транспортерных галерей следует принимать равной:

ПРЕДЕЛЬНЫЕ ГИБКОСТИ СЖАТЫХ ЭЛЕМЕНТОВ

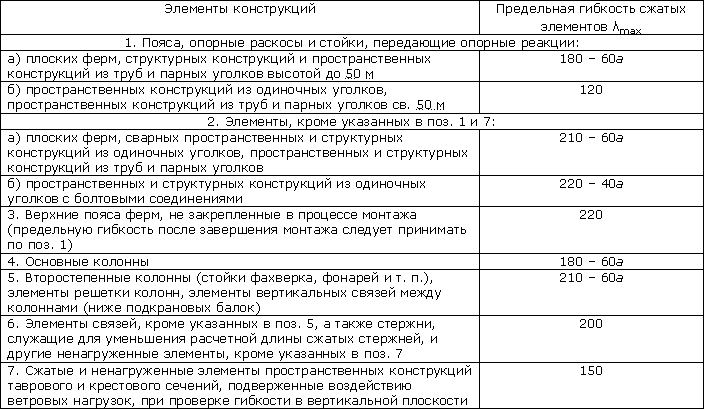
6.15*. Гибкости сжатых элементов не должны превышать значений, приведенных в табл. 19*.

Таблица 19*

Предельная гибкость сжатых элементов

1. Пояса, опорные раскосы и стойки, передающие опорные реакции:

а) плоских ферм, структурных конструкций и пространственных конструкций из труб и парных уголков высотой до 50 м

б) пространственных конструкций из одиночных уголков, пространственных конструкций из труб и парных уголков св. 50 м

2. Элементы, кроме указанных в поз. 1 и 7:

а) плоских ферм, сварных пространственных и структурных конструкций из одиночных уголков, пространственных и структурных конструкций из труб и парных уголков

б) пространственных и структурных конструкций из одиночных уголков с болтовыми соединениями

3. Верхние пояса ферм, не закрепленные в процессе монтажа (предельную гибкость после завершения монтажа следует принимать по поз. 1)

4. Основные колонны

5. Второстепенные колонны (стойки фахверка, фонарей и т. п.), элементы решетки колонн, элементы вертикальных связей между колоннами (ниже подкрановых балок)

6. Элементы связей, кроме указанных в поз. 5, а также стержни, служащие для уменьшения расчетной длины сжатых стержней, и другие ненагруженные элементы, кроме указанных в поз. 7

7. Сжатые и ненагруженные элементы пространственных конструкций таврового и крестового сечений, подверженные воздействию ветровых нагрузок, при проверке гибкости в вертикальной плоскости

Обозначение, принятое в таблице 19*:

— коэффициент, принимаемый не менее 0,5 (в необходимых случаях вместо j следует применять j_e).

ПРЕДЕЛЬНЫЕ ГИБКОСТИ РАСТЯНУТЫХ ЭЛЕМЕНТОВ

6.16*. Гибкости растянутых элементов не должны превышать значений, приведенных в табл. 20*.

Таблица 20*

Предельная гибкость растянутых элементов при воздействии на конструкцию нагрузок

динамических, приложенных непосредственно к конструкции

от кранов (см. прим. 4) и железнодорожных составов

1. Пояса и опорные раскосы плоских ферм (включая тормозные фермы) и структурных конструкций

2. Элементы ферм и структурных конструкций, кроме указанных в поз. 1

3. Нижние пояса подкрановых балок и ферм

4. Элементы вертикальных связей между колоннами (ниже подкрановых балок)

5. Прочие элементы связей

6*. Пояса, опорные раскосы стоек и траверс, тяги траверс опор линий электропередачи, открытых распределительных устройств и линий контактных сетей транспорта

7. Элементы опор линий электропередачи, кроме указанных в поз. 6 и 8

8. Элементы пространственных конструкций таврового и крестового сечений (а в тягах траверс опор линий электропередачи и из одиночных уголков), подверженных воздействию ветровых нагрузок, при проверке гибкости в вертикальной плоскости

Примечания: 1. В конструкциях, не подвергающихся динамическим воздействиям, гибкость растянутых элементов следует проверять только в вертикальных плоскостях.

2. Гибкость растянутых элементов, подвергнутых предварительному напряжению, не ограничивается.

3. Для растянутых элементов, в которых при неблагоприятном расположении нагрузки может изменяться знак усилия, предельную гибкость следует принимать как для сжатых элементов, при этом соединительные прокладки в составных элементах необходимо устанавливать не реже чем через 40i.

4. Значения предельных гибкостей следует принимать при кранах групп режимов работы 7К (в цехах металлургических производств) и 8К по ГОСТ 25546-82.

5. К динамическим нагрузкам, приложенным непосредственно к конструкциям, относятся нагрузки, принимаемые в расчетах на выносливость или в расчетах с учетом коэффициентов динамичности.

7. ПРОВЕРКА УСТОЙЧИВОСТИ СТЕНОК И ПОЯСНЫХ ЛИСТОВ ИЗГИБАЕМЫХ И СЖАТЫХ ЭЛЕМЕНТОВ

СТЕНКИ БАЛОК

7.1. Стенки балок для обеспечения их устойчивости следует укреплять:

поперечными основными ребрами, поставленными на всю высоту стенки;

поперечными основными и продольными ребрами;

поперечными основными и промежуточными короткими ребрами и продольным ребром (при этом промежуточные короткие ребра следует располагать между сжатым поясом и продольным ребром).

Прямоугольные отсеки стенки (пластинки), заключенные между поясами и соседними поперечными основными ребрами жесткости, следует рассчитывать на устойчивость. При этом расчетными размерами проверяемой пластинки являются:

Рис. 10. Расчетная высота стенки составной балки

Рис. 11. Схемы поперечных сечений гнутых профилей

7.2*. Расчет на устойчивость стенок балок следует выполнять с учетом всех компонентов напряженного состояния (s, t и s_loc).

Напряжение s, t и s_loc следует вычислять в предположении упругой работы материала по сечению брутто без учета коэффициента j_b.

Сжимающее напряжение s у расчетной границы стенки, принимаемое со знаком «плюс», и среднее касательное напряжение t следует вычислять по формулам:

Местное напряжение s_loc в стенке под сосредоточенной нагрузкой следует определять согласно требованиям пп. 5.13 и 13.34* (при g_f1 = 1,1) настоящих норм.

В отсеках, где сосредоточенная нагрузка приложена к растянутому поясу, одновременно должны быть учтены только два компонента напряженного состояния: s и t или s_loc и t.

Односторонние поясные швы следует применять в балках, в которых при проверке устойчивости стенок значения левой части формулы (74) не превышают 0,9g_c при

Источник

6. Расчетные длины и предельные гибкости элементов стальных конструкций

6.5*. Расчетные длины lef и радиусы инерции сечений i сжатых и ненагруженных элементов из одиночных уголков при определении гибкости следует принимать по табл. 13*.

Обозначения, принятые в табл. 13* (рис. 9*):

1. Раскосы по рис. 9*, а, д, е в точках пересечения должны быть скреплены между собой.

2. Для раскосов по рис. 9*, е необходима дополнительная проверка их из плоскости грани с учетом расчета по деформированной схеме.

3. Значение lef для распорок по рис 9*, в дано для равнополочных уголков.

Расчетные длины lef и радиусы инерции i растянутых элементов из одиночных уголков при определении гибкости следует принимать:

для перекрестных раскосов по рис. 9*, а, д, е:

Расчетные длины lef и радиус инерции i элементов из труб или парных уголков следует принимать согласно требованиям подраздела «Расчетные длины элементов плоских ферм и связей».

Расчетные длины элементов структурных конструкций

6.7. Расчетные длины lef элементов структурных конструкций следует принимать по табл. 17.

Радиусы инерции сечений i элементов структурных конструкций при определении гибкости следует принимать:

для сжато-изгибаемых элементов относительно оси, перпендикулярной или параллельной плоскости изгиба (i = ix или i = iy);

Расчетные длины колонн (стоек)

6.8. Расчетные длины lef колонн (стоек) постоянного сечения или отдельных участков ступенчатых колонн следует определять по формуле

6.9*. Коэффициенты расчетной длины M колонн и стоек постоянного сечения следует принимать в зависимости от условий закрепления их концов и вида нагрузки.

Для некоторых случаев закрепления и вида нагрузки значения M приведены в прил. 6, табл. 71, а.

6.10*. Коэффициенты расчетной длины колонн постоянного сечения в плоскости рамы при жестком креплении ригелей к колоннам следует определять:

для свободных рам при одинаковом нагружении верхних узлов по формулам табл. 17, а;

Элементы структурных конструкций

Расчетная длина l_ef

1. Кроме указанных в поз. 2 и 3

2. Неразрезные (не прерывающиеся в узлах) пояса и прикрепляемые в узлах сваркой впритык к шаровым или цилиндрическим узловым элементам

3. Из одиночных уголков, прикрепляемых в узлах одной полкой:

а) сварными швами или болтами (не менее двух),расположенными вдоль элемента, при l / i_min:

« 120 « 150 (только для элементов решетки)

св. 150 до 200 (только для элементов решетки)

б) одним болтом при l / i_min:

« 120 « 150 (только для элементов решетки)

св. 150 до 200 (только для элементов решетки)

Обозначение, принятое в табл. 17:

6.11*. Коэффициенты расчетной длины M отдельных участков ступенчатых колонн в плоскости рамы следует определять согласно прил. 6.

При определении коэффициентов расчетной длины M для ступенчатых колонн рам одноэтажных производственных зданий разрешается:

не учитывать влияние степени загружения и жесткости соседних колонн;

определять расчетные длины колонн лишь для комбинации нагрузок, дающей наибольшие значения продольных сил на отдельных участках колонн, и получаемые значения M использовать для других комбинаций нагрузок;

для многопролетных рам (с числом пролетов два и более) при наличии жесткого диска покрытия или продольных связей, связывающих поверху все колонны и обеспечивающих пространственную работу сооружения, определять расчетные длины колонн как для стоек, неподвижно закрепленных на уровне ригелей;

для одноступенчатых колонн при соблюдении условий l2/l1 M 0,6 и N1/N2 M 3 принимать значения M по табл. 18.

6.13. Расчетные длины колонн в направлении вдоль здания (из плоскости рам) следует принимать равными расстояниям между закрепленными от смещения из плоскости рамы точками (опорами колонн, подкрановых балок и подстропильных ферм; узлами креплений связей и ригелей и т.п.). Расчетные длины допускается определять на основе расчетной схемы, учитывающей фактические условия закрепления концов колонн.

Источник