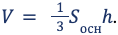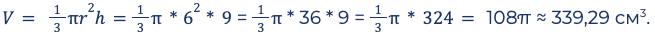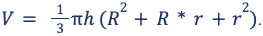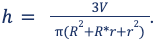Что такое усеченный конус
Что такое усеченный конус: определение, основные элементы
В данной публикации мы рассмотрим определение и основные элементы усеченного конуса. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение усеченного конуса
Усеченный конус (конический слой) – это геометрическая фигура в пространстве; часть конуса, оставшаяся между его основанием и секущей плоскостью, параллельной этому основанию.
Примечание: В рамках данной публикации мы будем рассматривать самый распространенный вид усеченного конуса – прямой круговой.
Усеченный конус образуется путем вращения на 360° прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию, или равнобедренной трапеции вокруг своей оси симметрии на 180°.
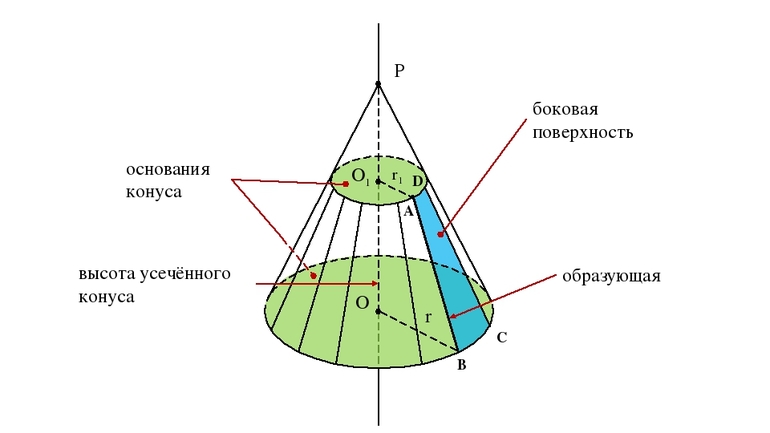
На рисунке ниже конус образован путем вращения равнобедренной трапеции ABCD вокруг оси O1O2.
Основные элементы усеченного конуса
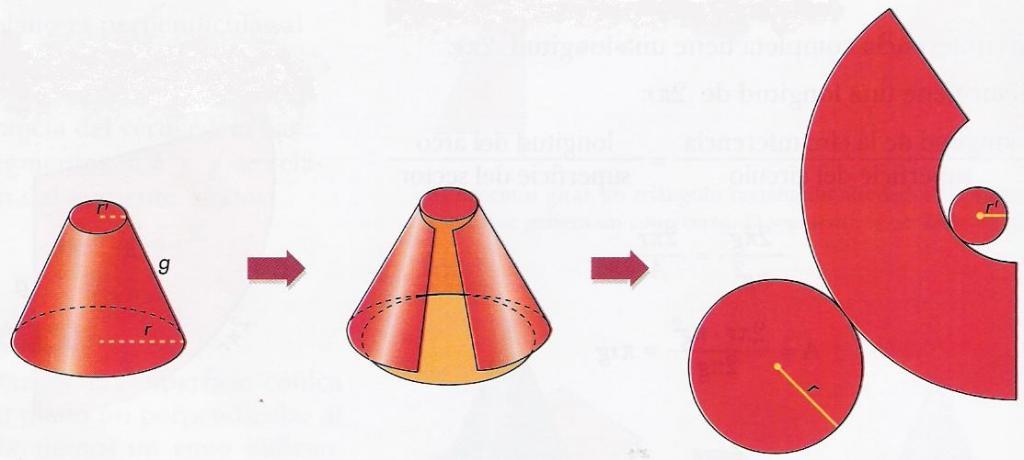
Развёртка боковой поверхности усеченного конуса выглядит следующим образом:
Длина бОльшей (меньшей) дуги равна длине окружности соответствующего основания конуса ( 2πR или 2πr ).
Рассмотрение свойств объемных фигур является одной из приоритетных задач геометрии. Важными характеристиками всех пространственных фигур являются объем и площадь поверхности. В статье раскрывается вопрос о том, что это — усеченный конус, и приводятся формулы для определения площади его поверхности и объема.
Фигура конус
Вам будет интересно: «Земляк» – это соотечественник и поддержка на чужбине
Расстояние между вершиной фигуры и основанием называется высотой. Если соответствующий перпендикуляр пересекает основание в геометрическом центре, то фигуру называют прямой.
Вам будет интересно: Полиакриловая кислота: способ получения, свойства, структура и практическое применение
Дальше в статье покажем, как, используя прямой круглый конус, получить усеченную фигуру.
Усеченный конус и способы его получения
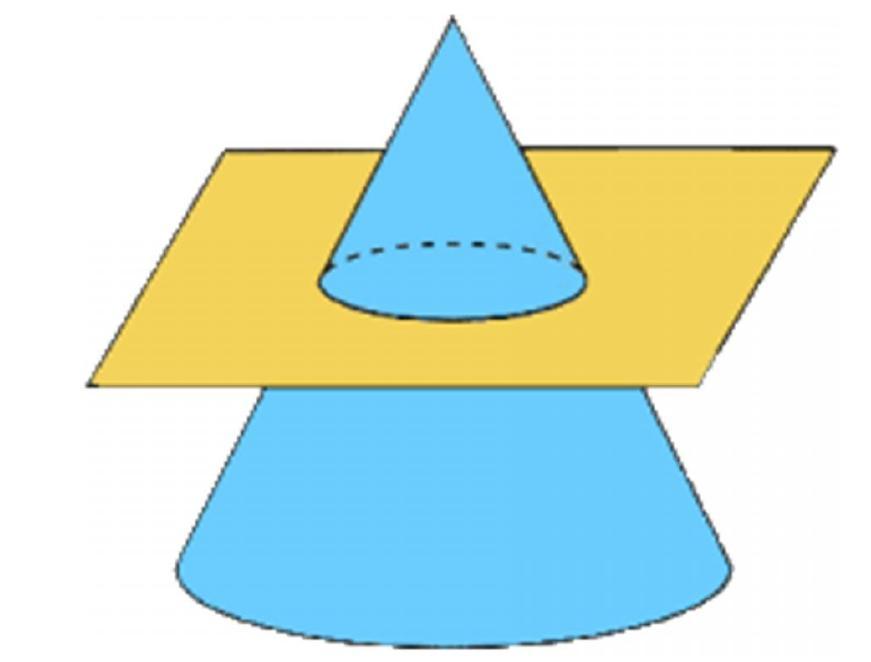
Предположим, что у нас имеется фигура, которая была показана в предыдущем пункте. Возьмем плоскость, параллельную основанию конуса, и отсечем с помощью нее вершину фигуры. Этот процесс показан на рисунке.
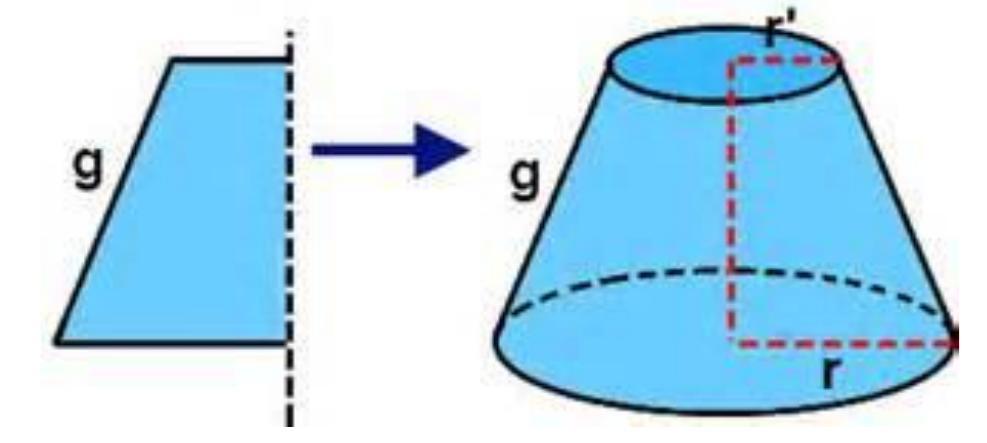
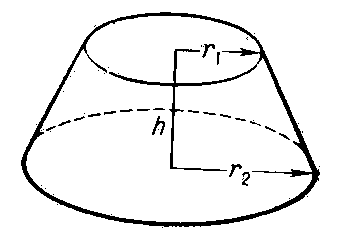
Существует еще один способ получения рассматриваемой фигуры. Предположим, что имеется некоторая трапеция с двумя прямыми углами. Если вращать эту трапецию вокруг стороны, к которой прямые углы прилегают, то она опишет поверхность усеченного конуса. Этот способ получения фигуры демонстрирует схема ниже.
Сторона трапеции, вокруг которой выполнялось вращение, будет являться осью усеченного конуса. Отрезок, который на оси отсекают два основания фигуры, называется высотой. На рисунке отмечены образующая g и радиусы оснований конуса усеченного r и r’.
Наконец, третий способ получения усеченного конуса заключается в увеличении количества ребер усеченной пирамиды до бесконечного числа. Во время этого процесса пирамида постепенно перейдет в конус.
Любопытно отметить, что форма рассматриваемой геометрической фигуры в первом приближении в природе характерна для действующего вулкана, что отчетливо видно на следующей фотографии.
Элементы фигуры и ее линейные характеристики
Все четыре параметра используются для определения площади поверхности и объема.
Поверхность усеченного конуса
Как отмечалось, состоит поверхность фигуры из трех частей. Если отрезать каждое из оснований от фигуры, а затем вдоль образующей разрезать и развернуть боковую поверхность, то мы получим развертку усеченного конуса. Рисунок ниже показывает, как она выглядит.
Площади оснований усеченного конуса находятся по простой формуле для соответствующей величины круга:
С площадью боковой поверхности дело обстоит несколько сложнее. Можно заметить, что она представляет собой сектор круга, некоего радиуса G, у которого вырезали центральную часть радиусом G-g. Если это учесть, то можно получить формулу для площади боковой поверхности Sb. Здесь ограничимся лишь приведением конечного выражения:
Это выражение можно записать через радиусы и высоту h, однако тогда оно будет иметь несколько громоздкий вид.
Складывая записанные выражения, получаем формулу для определения площади S всей поверхности усеченного конуса:
S = So1 + So2 + Sb = pi × r12 + pi × r22 + pi × (r1 + r2) × g =
= pi × (r12 + r22 + (r1 + r2) × g)
Объем фигуры
Как и любая фигура в пространстве, усеченный конус тоже обладает некоторым объемом. Этот объем ограничен двумя основаниями и боковой поверхностью. Здесь не будем приводить подробный вывод соответствующей формулы для V. Запишем, как и в случае с площадью поверхности, лишь конечный результат:
V = h × pi / 3 × (r12 + r22 + r1 × r2)
Эта формула, в отличие от выражения для площади S, в качестве параметров содержит радиусы усеченного конуса и его высоту.
Далее в статье покажем, как следует использовать приведенные формулы для решения конкретной геометрической задачи.
Задача на определение площади и объема усеченного конуса
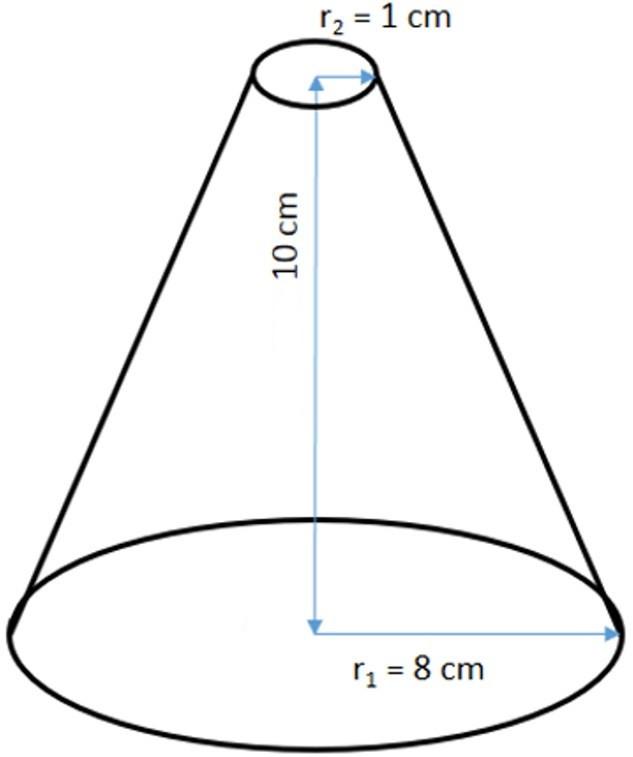
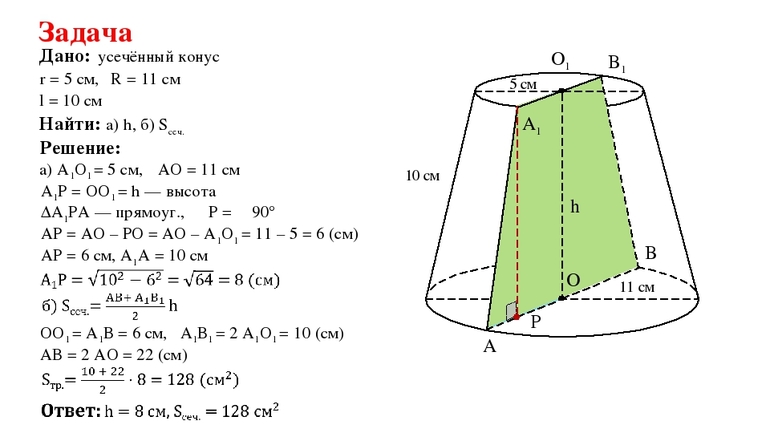
Ниже на рисунке изображен усеченный конус и приведены его линейные параметры. Необходимой найти площадь поверхности и объем фигуры.
Начнем решать задачу с определения величины V. Ее вычисление не представляет никакого труда, поскольку известны все необходимые параметры. Подставляя их в формулу для V, получаем:
V = h × pi / 3 × (r12 + r22 + r1 × r2) =
= 10 × 3,14 / 3 × (82 + 12 + 8 × 1) ≈ 764,07 см3
Найденное значение соответствует 0,76 литра.
Чтобы найти площадь поверхности S, следует сначала вычислить длину образующей g фигуры. Она будет равна:
Значение образующей g мы округлили до сотых. Теперь можно воспользоваться формулой для площади S:
S = pi × (r12 + r22 + (r1 + r2) × g) = 3,14 × (82 + 12 + (8 + 1) × 12,21) ≈ 549,15 см2
Заметим, что формулы для V и S, которые мы использовали при решении задачи, справедливы только для круглого прямого усеченного конуса. В случае наклонной фигуры или же фигуры с некруглыми основаниями этими формулами пользоваться нельзя.
Исходный полный конус
Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.
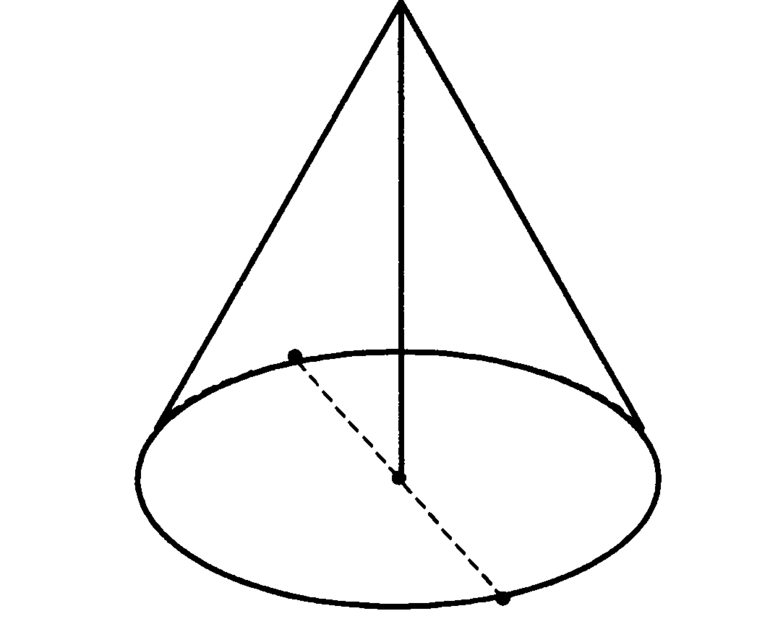
Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.
Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:
Существующие виды
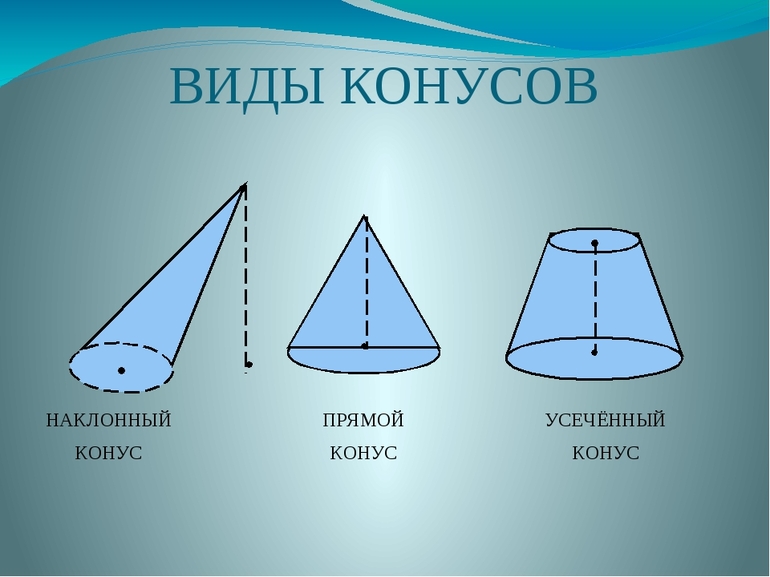
В геометрии известны несколько видов конуса. Каждый из них определяется характером директрисы и расположением относительно нее генератрисы. Выделяют следующие виды фигуры:
Круглая прямая фигура
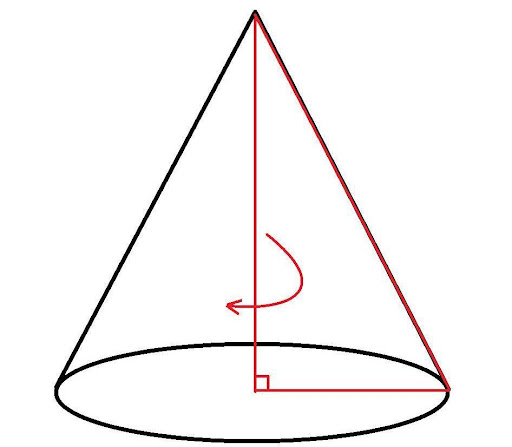
Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина — высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.
С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.
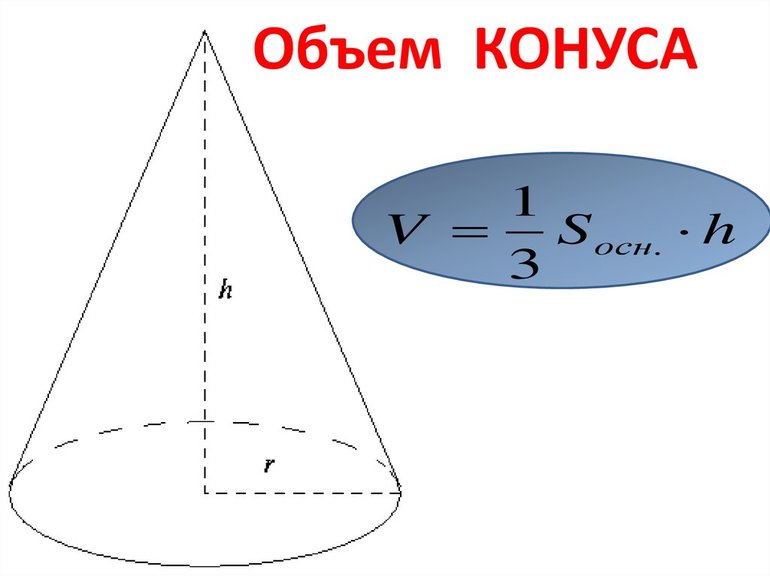
Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r 2 + pi*g*r, где число pi=3,14, r — радиус окружности в основании, g — длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.
Объем рассматриваемого конуса выражается следующей формулой: V = 1/3*pi*r 2 *h. Здесь h — высота фигуры. Можно заметить, что величина V ровно в три раза меньше аналогичной для цилиндра, имеющего то же основание, что и конус. Записанную формулу может вывести любой школьник, который знаком с интегральными вычислениями.
Усеченный геометрический объект
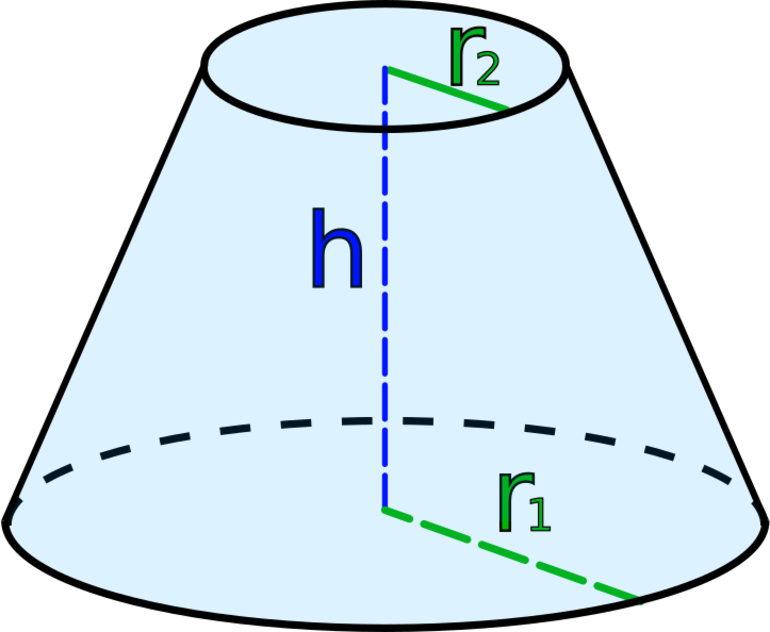
Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.
Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.
Способы построения
Можно выделить два основных способа построения усеченного круглого геометрического объекта:
В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной. Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.
Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.
Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.
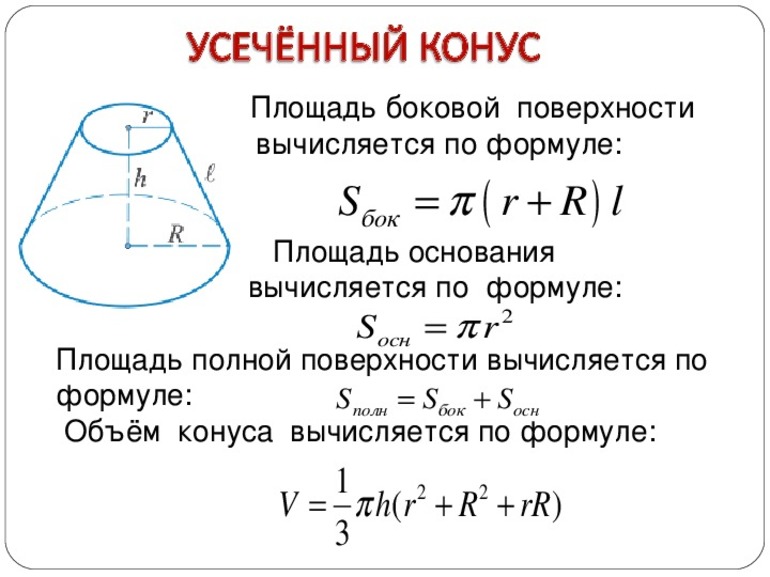
Площадь поверхности
Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:
S = S1 + S2 + Sb = pi*r1 2 + pi*r2 2 + pi*g*(r1 + r2).
Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.
Формула объема
Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:
V = 1/3*pi*r1 2 *H — 1/3*pi*r2 2 *(H-h).
Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:
V = 1/3*pi*h*(r1 2 + r2 2 + r1*r2).
Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:
V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).
Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.
Пример решения задачи
Из данных задачи можно определить значение каждого радиуса. Для этого необходимо ввести следующее равенство: r1 = 2*r2. Тогда для суммы площадей оснований можно записать выражение:
Откуда получается:
r2 = (S/(5*pi))^0,5 = (100/(5*3,14))^0,5 = 2,52 см.
Тогда радиус большего основания будет равен r1 = 2*r2 = 5,04 см.
Чтобы найти генератрису g усеченного конуса, следует рассмотреть прямоугольный треугольник, который образован двумя катетами: высотой h и отрезком r1-r2. Его гипотенуза является генератрисой, она равна:
g = ((r1-r2)^2 + h 2 )^0,5 = (2,52 2 + 15 2 )^0,5 = 15,21 см.
Поскольку известны все необходимые линейные параметры усеченной фигуры, можно воспользоваться известной формулой для площади ее боковой поверхности:
Таким образом, усеченный конус является фигурой вращения, поверхность которой состоит из оснований и боковой части. Чтобы воспользоваться формулами для определения его площади и объема, необходимо знать любые три его линейных параметра.
Усеченный конус: формула объема, площади поверхностей и другое
Содержание:
Конус – объемное тело, получаемое посредством вращения треугольника с углом 90° вокруг катета – его высоты. Расстояние от вершины до любой точки круга в основании тела называется образующей. Рассмотрим, как проводится расчет прямого и усеченного конусов: по каким формулам определяют их площади, объемы.
Понятие
Второй вариант образования рассматриваемого геометрического тела: прямоугольный треугольник вращается вокруг катета по или против часовой стрелки. Катет, ставший осью, будет высотой конуса, лежащий в основании – диаметром нижней поверхности, гипотенуза – образующей.
Разновидности конусов
Площадь
Площадь прямого конуса определяется по формуле:
Радиус – это половина диаметра: 12/2 = 6 см.
Подставим значения в выражение: S = πr (r + l).
Получим: S = π * 6 *(6 + 10) = 96 π ≈ 301,584 см2.
Как вычислить площадь усеченного конуса
Формула площади полной поверхности усеченного конуса:
S1 и S2 – площади поверхностей усеченного конуса.
Подставляем значения и упрощаем:
Зная радиусы – 6 и 10 см, расстояние от вершины к лежащей на круге точке – 12 см найдём площадь граней.
Объем усечённого конуса
Объем – пространство, занимаемое геометрическим телом. Численное значение указывает на количество кубиков с гранью единица, помещающихся в конусе. Объем тела вычисляется как треть произведения площади основания на его высоту.
.
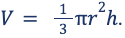
Пример: вычислить объем тела: r = 6 см, h = 9 см. Ставим значения в формулу, пошагово упрощаем выражение.
Если известен диаметр, разделите его на два: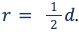 
.
Вычислим объем усеченного конуса. Для понимания, от полного объема исходного тела нужно отнять значение отрезанного параллельной нижней грани плоскостью.
Формула объема усеченного конуса:
Высота
Существует несколько способов как найти высоту усеченного конуса. Какой подойдёт, зависит от исходных данных.
Когда даны радиусы оснований и объем, достаточно провести вычисления:
Для прямого при известном радиусе или диаметре оснований с образующей можно воспользоваться теоремой Пифагора:
Усечённый конус
Смотреть что такое «Усечённый конус» в других словарях:
усечённый конус — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN truncated cone … Справочник технического переводчика
УСЕЧЁННЫЙ — УСЕЧЁННЫЙ, усечённая, усечённое; усечён, усечена, усечено. 1. прич. страд. прош. вр. от усечь (книжн.). 2. Такой, у которого верхняя часть отсечена плоскостью, параллельной основанию (о конусе, пирамиде; мат.). Усечённый конус. Усеченная пирамида … Толковый словарь Ушакова
усечённый — ая, ое.; матем. Такой, у которого верхняя часть отсечена плоскостью, параллельной основанию. Усечённый конус. У ая пирамида … Словарь многих выражений
УСЕЧЁННЫЙ — УСЕЧЁННЫЙ, ая, ое. В математике: такой, у к рого вершинная часть отделена, отсечена плоскостью, параллельной основанию. У. конус. Усечённая пирамида. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
усечённый — ая, ое. 1. прич. страд. прош. от усечь. 2. в знач. прил. мат. Такой, у которого верхняя часть отсечена плоскостью, параллельной основанию. Усеченный конус. Усеченная пирамида. 3. в знач. прил. грамм., лит. С усечением (во 2 знач.), представляющий … Малый академический словарь
Конус — Прямой круговой конус. Прямой и … Википедия
КОНУС — (лат. conus, от греч. konos) коническая поверхность множество прямых (образующих) пространства, соединяющих все точки нек рой линии (направляющей) с данной точкой (вершиной) пространства. Простейший К. круглый, или прямой круговой, направляющей к … Большой энциклопедический политехнический словарь
Конус — (лат. conus, от греч. konos) (математика), 1) К., или коническая поверхность, геометрическое место прямых (образующих) пространства, соединяющих все точки некоторой линии (направляющей) с данной точкой (вершиной) пространства.… … Большая советская энциклопедия
Построение разверток тел вращения — Окружающий нас мир динамичен и разнообразен, и далеко не всякий объект можно просто обмерить линейкой. Для подобного переноса используются специальные техники, как то триангуляция. Потребность в составлении сложных развёрток, как правило,… … Википедия