Что такое уравнение движения материальной точки

Уравнение движения материальной точки

Вы будете перенаправлены на Автор24

Система отсчета. Системы координат

Под движением материальной точки в пространстве понимают изменение ее положения относительно некоторых тел с течением времени. В связи с этим можно говорить только о движении в некоторой системе отсчета.

Сами по себе точки пустого пространства неразличимы между собой, поэтому говорить о той или иной точке пространства можно, если в ней находится материальная точка. Ее положение и определяется относительно тела отсчета с помощью измерений, для чего с телом (телами) отсчета жестко связывается некоторая система координат; в ней и измеряются пространственные координаты. Например, на поверхности Земли это географическая широта и долгота точки.

В теоретических рассуждениях часто не принимают во внимание реальную систему отсчета, сохраняя только систему координат, которая и служит математической моделью системы отсчета, применяемой при измерениях на практике.

Кинематическое уравнение движения материальной точки

Итак, в любой системе отсчета и системе координат имеется возможность определить координаты материальной точки в любой момент времени.

Если положение материальной точки в каждый момент времени определено в данной системе отсчета, то движение ее задано или описано.

Это задание достигается в виде кинематического уравнения движения:

Аналитически положение точки всегда определяется совокупностью трех независимых между собой чисел. Этот факт выражают словами: свободная точка имеет три степени свободы движения.

Готовые работы на аналогичную тему

В этом случае кинематические уравнения движения точки имеют следующий общий вид:

$r=r(t),\varphi =\varphi (t)$. (3)

кинематические уравнения движения точки запишутся так:

(Это могут быть сферические, цилиндрические и другие координаты).

Это уравнение является уравнением движения точки по траектории. Такой способ задания движения называется естественным или траекторным.

Координатный и естественный способы задания движения точки физически (в смысле фиксации ее положения в пространстве)

Закон движения точки по траектории может быть задан аналитически, графически или в виде таблицы. Оба последних способа широко применяются на транспорте (например, графики и расписания движения поездов).

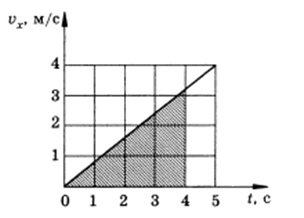
Решение: Зависимость скорости от времени имеет вид:

Запишем уравнение зависимости координаты от времени и сравним его с данным:

Подставим полученные данные в уравнение скорости и получим:

Определим точки и построим график:

Путь, пройденный телом, численно равный площади фигуры, ограниченной графиком и может быть найден по следующей формуле:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 01 07 2021

Источник

Теоретическая механика

26. Динамика материальной точки. Законы Ньютона. Уравнения движения материальной точки

Динамика есть часть теоретической механики, в которой устанавливается и изучается связь между движением материальных тел и действующими на них силами.

В основе динамики лежат эмпирические законы, точно сформулированные и систематически изложенные независимо друг от друга Ньютоном и Галилеем.

Если на материальную точку не действуют никакие силы или действующая система сил является уравновешенной, то материальная точка находится в состоянии покоя или равномерного и прямолинейного движения. Такое состояние точки называется инерциальным.

3. Закон равенства сил действия и противодействия.

Силы, с которыми действуют друг на друга две материальные точки, всегда равны по модулю и направлены по прямой, соединяющей эти точки, в противоположные стороны.

3′. Закон независимости действия сил.

Если на материальную точку действует система сил, то точка получит ускорение равное геометрической сумме ускорений, которые приобрела бы точка под действием каждой силы в отдельности.

Уравнение (1) называется основным уравнением динамики точки.

Дифференциальное уравнение движения материальной точки

Таким образом, можно записать

Уравнение (2) является основным дифференциальным уравнением движения материальной точки, записанное в векторном виде.

Координатная форма записи основного дифференциального уравнения движения точки

Разложим радиус-вектор и результирующую силу по осям координат

Подставим (3) в (2), получим

Система уравнений (5) является координатной формой записи основного дифференциального уравнения движения точки.

Источник

Уравнение движения материальной точки

Что такое движение материальной точки

В механике рассматривают перемещение объектов. Принципы характерны для материальной точки и твердого тела. Термин «материальная точка» введен с целью упростить решение практических задач. В случае, когда габариты объекта существенно меньше, чем расстояние, которое он преодолевает, либо размеры других тел, то условно данный объект обозначают материальной точкой.

Кинематика — раздел механики, изучающий математическое описание движения идеализированных тел, без рассмотрения причин движения.

Движением материальной точки в пространстве называют изменение ее положения по отношению к другим телам с течением времени.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Для расчета физических характеристик самолета относительно Земли в полете можно представить его в виде материальной точки. Однако если рассматривается система, которая включает самолет и пассажира, летящего в нем, то в данном случае принимать транспортное средство за материальную точку нецелесообразно. Таким образом, движение материальной точки рассматривают только в том случае, когда размерами объекта в конкретной ситуации можно пренебречь.

В одинаковое время положение точки в пространстве может отличаться в зависимости от того, относительно какого тела осуществляются наблюдения. С помощью системы координат и тела отсчета описывают перемещение материальной точки в пространстве. Согласно элементарным математическим закономерностям, задать положение какой-либо точки на плоскости можно, воспользовавшись системой координат.

Прямые, которые взаимно перпендикулярны и пересекаются в одной точке, являются координатными прямыми. А данная точка пересечения носит название начала координат.

Из начала координат можно вывести еще одну прямую, которая будет являться перпендикуляром к плоскости. Подобная система позволит задать положение точки в пространстве. Другим методом является применение радиус-вектора.

Радиус-вектор представляет собой отрезок, который провели из точки начала координат к заданной точке.

В течение времени движущаяся материальная точка меняет свое положение в пространстве. Для того чтобы выполнить расчет положения точки в какой-либо определенный момент времени, необходимо провести измерения времени.

Совокупность тела отсчета, связанной с ним системы координат и прибора отсчета времени представляет собой систему отсчета.

Выбор системы отсчета определяется следующими характеристиками:

Можно рассмотреть движение двух автомобилей, которые находятся на соседних полосах и перемещаются в одном направлении с равными скоростями. Когда телом отсчета является одно из этих транспортных средств, при заданной системе отсчета скорость, путь и перемещение второго транспорта будут иметь нулевые значения. Таким образом, второй автомобиль по сравнению с первым находится в состоянии покоя. В случае, когда в качестве тела отсчета выбрана дорога, значения скорости, пути и перемещения будут отличны от нуля.

Траектория материальной точки — линия, которую очерчивает материальная точка, двигаясь в пространстве.

Траектория включает множество точек, в которых рассматриваемая материальная точка была зафиксирована в прошедший момент времени, находится в данное время и будет замечена в будущий временной период.

Перемещением материальной точки называют вектор, берущий начало в точке траектории в начальный промежуток времени и заканчивающийся в точке траектории в конечный момент времени.

Путь материальной точки представляет собой сумму всех отрезков, пройденных материальной точкой в процессе движения.

Путем называют скалярную величину, которая всегда характеризуется положительным значением. При перемещении материальной точки пройденный ей путь может только увеличиваться.

Амплитуда — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении.

Система отсчета и координат

Точки, которые присутствуют в пустом пространстве, не различают. Рассуждать о точке целесообразно, когда в ней находится материальная точка. Система координат позволяет выполнить измерения, которые необходимы для вычисления пространственных координат. Исходя из полученных данных, определяют положение материальной точки в пространстве. В качестве примера можно рассмотреть поверхность нашей планеты. Тогда для определения положения необходимо вычислить широту и долготу заданной точки.

В теоретических расчетах применяют декартову прямоугольную систему координат. С ее помощью можно определить положение точки при условии наличия радиус-вектора \(\bar\) и трех проекций x, y, z, которые являются координатами точки.

Другие способы решения задачи на определение положения материальной точки:

В теоретических расчетах, как правило, пренебрегают реальной системой отсчета. Обычно для измерений используют ту систему, которая является математической моделью реальной, применяемой для практических исследований.

Какому закону подчиняется движение точки в пространстве

Кинематические законы движения

Механическое движение представляет собой изменение положения тела по отношению к другим телам, входящим в систему отсчета. Для описания движения тела выбирают систему отсчета, состоящую из следующих компонентов:

Основными способами описания движения тела являются:

Если тело рассматривают в рамках декартовой системы координат, то положение материальной точки М определяется с помощью радиус-вектора \(\bar\) и трех координат x, y, z. Радиус-вектор проводят из начала системы координат к рассматриваемой точке.

Во время движения материальной точки фиксируют изменение ее координат:

С помощью данных формул можно рассчитать перемещение точки координатным методом. Радиус-вектор будет определяться, согласно следующему уравнению:

где \(\bar, \bar,\bar\) являются единичными векторами по осям X,Y,Z.

Векторное кинетическое уравнение движения материальной точки будет записано таким образом:

Представленные уравнения являются кинетическими законами движения материальной точки. Эти закономерности необходимы для полноценного описания перемещения токи в пространстве. Найти модуль или длину радиус-вектора можно с помощью формулы:

Динамические законы движения материальной точки

В динамике движение материальной точки рассматривают, исходя из воздействия сил, приложенных к рассматриваемой точке. Ключевые закономерности классической динамики сформулировал Ньютон.

Первый закон Ньютона определяет тот факт, что материальная точка находится в состоянии покоя или перемещается равномерно и прямолинейно при отсутствии воздействия на нее внешних сил или, когда действие этих сил взаимно скомпенсировано.

Второй закон Ньютона гласит, что для инерционных систем отсчета результирующая сил, которые приложены к материальной точке, равна произведению ее массы и ускорения.

В виде формулы второй закон Ньютона можно записать следующим образом:

Дифференциальные уравнения для перемещения материальной точки записывают в таком виде:

где х, у, z являются координатами движущейся материальной точки,

\(>, >, >\) представляют собой проекции сил, которые воздействуют на точку.

Согласно дифференциальным уравнениям движения материальной точки, зная массу, можно найти силы, которые оказывают на рассматриваемую точку воздействие.

Кинематическое уравнение движения материальной точки

В любой системе отсчета или координат можно определить координаты материальной точки в разные моменты времени. Если определены положение и материальная точка в какой-либо системе отсчета, ее перемещение называют заданным или описанным. Такое условие соблюдается, благодаря применению кинематического уравнения движения:

Аналитическим положением точки является совокупность трех чисел, которые не зависят друг от друга, то есть трех степеней свободы движения.

При наличии указанного положения в любой момент времени t считается, что движение точки, согласно первому уравнению, определено. В этом случае необходимо задать декартовы координаты точки в виде однозначных и непрерывных функций времени:

Прямоугольными декартовыми координатами x, y, z являются проекции радиус-вектора, который выведен из начала координатной системы. Понятно, что длина и направление радиус-вектора рассчитывается из соотношений, в которых a, β, γ представляют собой углы с координатными осями, которые образованы радиус-вектором. Таким образом, кинематическими уравнениями движения материальной точки в декартовых координатах будут следующие равенства:

Данные формулы можно записать с помощью другой системы координат, связанной с декартовой по средствам однозначных преобразований. В случае, когда точка перемещается в плоскости Оху, можно воспользоваться полярными координатами r, ϕ, которые относятся к декартовым преобразованиям. При этом используют формулу движения точки, записанную следующим образом:

Кинематическое уравнение для описания перемещения точки в криволинейных координатах q₁, q₂, q₃, которые связаны с декартовыми преобразованиями:

будет представлено в следующей форме:

Кривая радиус-вектора, которую описывает конец вектора в процессе перемещения точки, совпадает с ее траекторией. Параметрическим уравнением траектории с t являются следующие равенства:

Исключая время из кинематических уравнений, получают вид координатного уравнения траектории. Для того чтобы определить движение точки, необходимо задать ее траекторию и мгновенное положение точки на ней. Положение точки на кривой рассчитывают по средствам лишь одной характеристики, которой является расстояние вдоль кривой от некого начала отсчета с положительным направлением:

Данная формула представляет собой уравнение движения точки по траектории. Метод его записи является естественным или траекторным. Установлена физическая эквивалентность понятий координатного и естественного метода задания движения материальной точки. С точки зрения математики, данное положение представляет собой возможность использования разных методик в зависимости от конкретных условий задачи. Задать такую закономерность можно с помощью аналитических, графических или табличных средств.

Источник

Уравнение движения точки

Всего получено оценок: 29.

Всего получено оценок: 29.

Кинематика — это раздел физики, который изучает движение без исследования его причин. С помощью кинематических закономерностей движения можно рассчитать, в каком месте будет находиться тело в тот или иной момент времени. Эти закономерности описываются с помощью математических формул, называемых «уравнения движения». Рассмотрим эту тему более подробно.

Движение материальной точки

Материальная точка — это тело, имеющее массу, размерами которого в данный момент можно пренебречь. Понятие материальной точки очень удобно в кинематике и динамике, поскольку позволяет исключить несущественные стороны исследуемого движения и сосредоточиться на основных параметрах.

Рис. 1. Материальная точка.

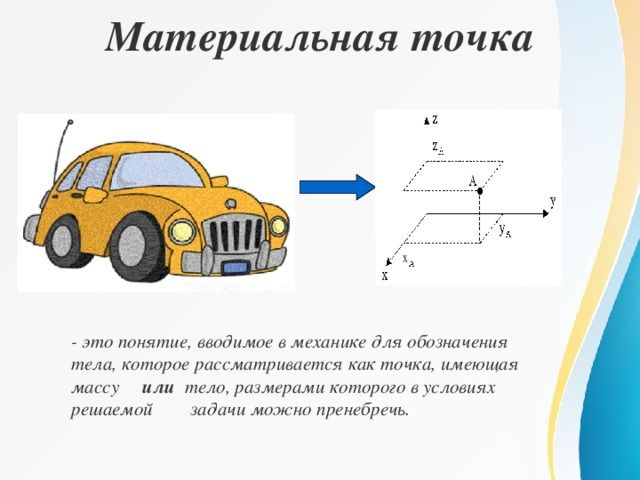
Материальная точка находится в некоторой системе отсчёта, поэтому ей можно приписать некоторые координаты — одну, две или три, в зависимости от числа координатных осей.

Движение материальной точки состоит в том, что некоторые из координат меняются с течением времени. Следовательно, для описания движения необходимо сопоставить каждому моменту времени соответствующие координаты. Сделать это можно различными способами, например, просто составив таблицу, в первом столбце которой стоят моменты времени, а в остальных столбцах — соответствующие координаты. Однако удобнее найти математическую формулу, в которой в качестве исходной независимой переменной берётся время, а результатом формулы является координата.

Рис. 2. Точка в системе координат

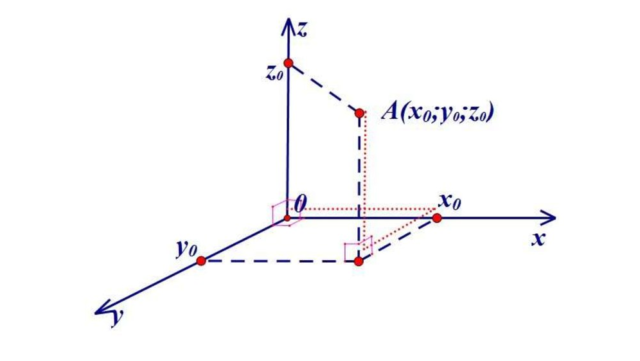
Уравнения движения точки

Математические формулы, с помощью которых можно найти координаты точки в любой момент времени, называются уравнениями движения материальной точки.

Примером самого простого уравнения движения точки является формула:

Возьмём пример немного сложнее. Если точка движется с постоянной скоростью, то, как известно к 9 классу, умножив скорость на время движения, мы получаем пройденное расстояние. В виде формулы это выразится, например, следующим образом:

С помощью этой формулы мы можем выяснить, что в начальный момент времени точка находилась в начале координат (подставив нулевое время, мы получим нулевую координату). Подставляя другие значения времени, мы найдём соответствующую координату. Кроме того, из формулы можно получить и скорость, с которой движется материальная точка — 5 метров в секунду, или других единиц, принятых в системе отсчёта.

Если в начальный момент точка имела некоторую координату, допустим, 1 (метр), то её уравнение движения примет вид:

Наконец, в системе отсчёта может быть не одна, а несколько координатных осей. В этом случае движение материальной точки описывается системой уравнений. Например:

В данном случае описывается движение в трёхмерном пространстве точки, которая в начальный момент имела координаты (1; 3; 5) и скорость которой равна 7.

Для описания движения в системе отсчёта с несколькими координатами нередко используется векторный способ описания, когда все переменные в уравнении являются векторами. Записи получаются более компактными, хотя описывают те же самые координаты и движения.

Что мы узнали?

Уравнения движения точки — это математические формулы, связывающие время в принятой системе отсчёта с координатами точки в ней. Подставляя в эти уравнения различные моменты времени, можно получить положения точки в эти моменты. Кроме того, из уравнений движения можно получить скорость, с которой движется точка.

Источник

Физика

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Механическое движение. Система отсчёта. Закон относительности движения

Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.

То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).

Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.

Рисунок 1 – Иллюстрация к примеру

Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение.

Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета. То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение.

Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)

Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.

Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку.

Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.

Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.

Уравнения движения. Радиус-вектор. Проекция вектора

Для описания движения тела необходимо уметь рассчитывать его положение в каждый момент времени. Как это сделать?

Самый очевидный способ – координатный. Если вернуться к примеру на рисунке 2, можно увидеть, что летящий мяч в каждый момент времени имеет три координаты по осям OX, OY и OZ. Эти координаты являются функциями времени (т.е. они зависят от времени), а значит, их можно записать в виде системы:

Вид этих уравнений будет зависеть от многих вещей: от того, с какой силой бросили мяч в начале, от массы мяча, под каким углом его бросили и так далее. В любом случае, если эти уравнения заданы, можно найти координаты (то есть положение) тела в любой момент времени. Поиск этих уравнений – основная задача кинематики.

Эта система является кинематическими уравнениями движения тела или материальной точки, записанными в координатной форме. Повторим: если вид уравнений движения задан, можно узнать координату движущейся точки в любой момент времени.

В общем случае, координат три, но иногда можно обойтись двумя или даже одной координатой. Например, для описания движения бильярдного шара достаточно двух координат (так как шар не может двигаться вверх и вниз), а для описания движения шарика, катящегося по прямому горизонтальному желобку достаточно одной координаты (шарик не может двигаться вверх-вниз и вправо-влево).

Еще один способ описания движения – векторный.

*Перед дальнейшим прочтением данной статьи желательно вспомнить основную теорию по теме «Векторы» и «Метод координат»

Вектор, проведенный из начала координат к материальной точке, называется радиус-вектором (см. рисунок 3).

Рисунок 3 – Радиус-вектор (серой линией изображены траектория движения материальной точки, r₁ и r₂* радиус-векторы, проведенные к этой материальной точке в разные моменты времени)

Радиус-вектор проведенный к материальной точке в разные моменты времени будет разным. Значит, его тоже можно представить, как функцию времени:

r = r(t)

Такая функция и будет уравнением движения в векторной форме. Если ее вид задан, можно описать движение тела с той же полнотой, как и при координатной записи.

Еще раз обозначим отличия: при записи уравнения движения в координатной форме в каждый момент времени наблюдающий будет знать три координаты тела; при записи в векторной форме в каждый момент времени известен радиус-вектор (его модуль и направление). Обе записи равносильны.

*На письме векторы обычно обозначаются стрелкой сверху, над величиной. Однако в печатном тексте не всегда удобно нагромождать формулы дополнительными знаками, поэтому в печати векторные величины пишут просто жирным шрифтом. В данной статье далее жирным шрифтом будут написаны только векторные величины.

Покажем, что векторная и координатная записи равносильны. Для этого необходимо вспомнить, как построить проекцию вектора на ось (см. рисунок 4).

Рисунок 4 – Построение проекции вектора на ось

Если вектор выходит из начала координат, задача облегчается – необходимо опустить перпендикуляр только из конца вектора.

Напоминания из геометрии:

два вектора равны, если они параллельны или лежат на одной прямой, сонаправлены, а их модули равны;

проекции равных векторов равны.

Рассмотрим пример (см. рисунок 5)

Рисунок 5 – Задача на нахождение проекции векторов

Предлагаем читателю самому подумать, а затем сравнить свои рассуждения с приведенными ниже.

В двумерном случае, проецировать нужно на две оси, но принцип остается тем же.

Иногда еще нужно находить составляющие компоненты вектора а_х и а_у. Рассмотрим пример, для простоты возьмем вектор, выходящий из начал координат (см. рисунок 6).

Сумма векторов а_х и а_у равна а. Модули векторов а_х и а_у численно равны координатам точек, куда попали перпендикуляры, опущенные из конца вектора а на оси ОХ и ОУ.

Еще следует отметить, что, если известен угол β между вектором а и осью ОХ, воспользовавшись основами тригонометрии, можно найти величины проекций:

Если бы вектор а совпадал с радиус-вектором какой-нибудь точки, то величины а_х и а_у совпадали бы с координатами тела по осям ОХ и ОY.

Способ с использованием тригонометрических функций удобен, когда координата конца вектора попадает в нецелое число и опустив перпендикуляр на ось его трудно найти точно. В физических задачах такое часто случается.

Рисунок 6 – Нахождение компонент вектора а

Рассмотрим пример (см. рисунок 7). Модуль вектора r равен 2. Сам вектор направлен под углом в 45 градусов к оси ОХ. Необходимо найти величины проекций (они же координаты) этого вектора на оси ОХ и ОУ.

Рисунок 7 – Задача на нахождение проекций вектора в двумерном пространстве

В общем случае радиус-вектор находится в трехмерном пространстве (см. рисунок 8). Построение проекции осуществляется по тому же принципу, что и в рассмотренных выше примерах. Когда строятся проекции на оси ОХ и ОУ, перпендикуляр сначала опускается на плоскость, в которой лежат оси ОХ и ОУ, а затем точка, в которую упал перпендикуляр к плоскости, проецируется на оси ОХ и ОУ.

Точки, в которые попал перпендикуляры к осям – r_x, r_y, r_z – это и есть координаты x, y, z тела в текущий момент времени.

Следует оговориться, что большинство задач 10-го класса будут ограничиваться двумерным пространством.

Рисунок 8 – Построение проекций радиус-вектора

Траектория. Путь. Перемещение

Траектория – это линия, вдоль которой движется тело.

Траектория движения может быть прямолинейной, если тело движется по прямой линии, и криволинейной, если тело движется по кривой.

Путь (S), пройденный телом, равен длине траектории.

Перемещение (r)* – это вектор, проведенный из начала пути в конец.

В случае прямолинейного движения путь и модуль перемещения тела совпадают (см. рисунок 9а). В случае криволинейного – путь и перемещение различаются (см. рисунок 9б), так как длина линии движения тела больше длины вектора, соединяющего начало и конец траектории.

Рисунок 9 – Путь (S) и перемещение (r) при прямолинейном (а) и криволинейном (б) движении

Равномерное прямолинейное движение: скорость и уравнение движения

Путь и перемещение при равномерном прямолинейном движении

Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.

Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:

Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.

Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см. рисунок 8). Радиус-вектор, проведенный в точку A обозначим r₀, а радиус-вектор в точку Б обозначим r₁. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.

Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении

Тогда скорость движения (v) будет вычисляться по формуле:

Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.

Из этого выражения следует:

Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:

Данное уравнение является уравнением движения при прямолинейном равномерном движении.

*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t₁, где t – конечный момент времени, t₁ – начальный. Если же начальный момент времени совпадает с началом отсчета t₁ = 0, то △t = t – 0 = t_.

Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.

Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.

В этих выражениях r_0x, r_0y, r_0z и v_x, v_y, v_z – это компоненты изначальных векторов r₀ и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:

Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.

В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х₀) и конечной (х₁) точки на ось ОХ.

Рисунок 9 – Перемещение тела в координатном представлении

Уравнение координаты (х) движения будет выглядеть:

А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:

Если точка начала двигаться из начала отсчета S₀ = 0, можно переписать эту формулу в виде:

Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:

Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x₀ = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.

Итак, для начала приведем все единицы измерения к СИ:

Теперь можно записывать уравнение для координаты х:

Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:

x(2) = 0,03 + 5*2 = 10, 03.

А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2) = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:

S = x(2) – x₀ = 10, 03 – 0,03 = 10 м.

А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?

Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:

Источник