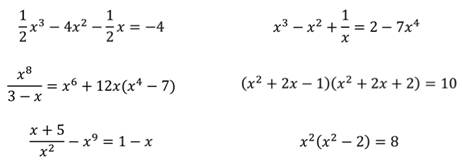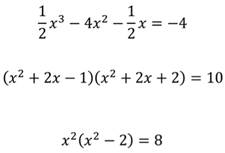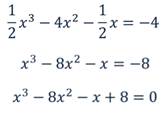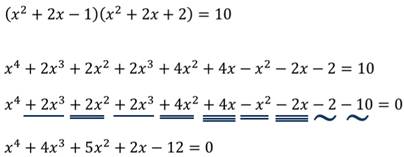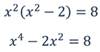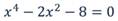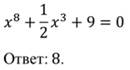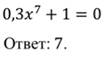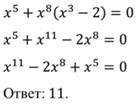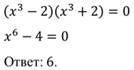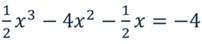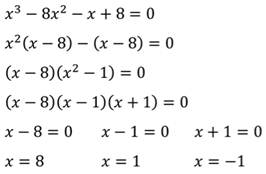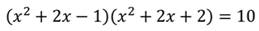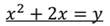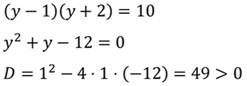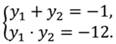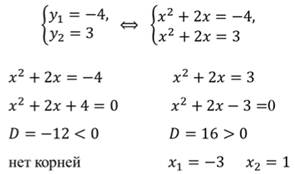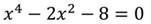Целое уравнение и его корни

В каждом из уравнений

обе части являются целыми выражениями. Такие уравнения называют, как известно, целыми уравнениями. Напомним, что

В уравнении (1) раскроем скобки, перенесем все члены в левую часть и приведем подобные члены. Получим

Выполним аналогичные преобразования в уравнении (2), умножив предварительно обе его части на 4:

В каждом из рассмотренных примеров мы выполняли такие преобразования, которые приводят к уравнению, равносильному данному. В результате получали уравнение, имеющее вид Р(х) = 0, где Р(х) — многочлен стандартного вида.

Вообще всякое целое уравнение можно заменить равносильным ему уравнением, левая часть которого — многочлен стандартного вида, а правая — нуль.

Например, уравнение (1) является уравнением пятой степени, а уравнение (2) — уравнением четвертой степени.

Уравнение первой степени можно привести к виду ах + b = 0, где х — переменная, а и b — некоторые числа, причем а ≠ 0. Из уравнения ах + b = 0 при а ≠ 0 получаем, что Число — корень уравнения. Каждое уравнение первой степени имеет один корень.

Для уравнений третьей и четвертой степеней известны формулы корней, но эти формулы очень сложны и неудобны для практического применения. Для уравнений пятой и более высоких степеней общих формул корней не существует.

Заметим, что иногда удается решить уравнение третьей и более высокой степени, применяя какой-либо специальный прием. Например, некоторые уравнения нетрудно решить с помощью разложения многочлена на множители.

Источник

Рациональные уравнения (ЕГЭ 2022)

Рациональные уравнения – это уравнения, в которых и левая, и правая части – рациональные выражения.

Ну… Это было сухое математическое определение, и слово-то какое: «рациональные». А по сути, рациональные выражения – это просто целые и дробные выражения без знака корня.

А получается, что под пугающим «рациональным уравнением» скрывается всего лишь уравнение, в котором могут присутствовать сложение, вычитание, умножение, деление и возведение в степень с целым показателем, но НЕ корень из переменной.

Рациональные уравнения — коротко о главном

Определение рационального уравнения:

Рациональное уравнение – это равенство двух рациональных (без знака корня) выражений.

Дробно-рациональное уравнение – рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.

Алгоритм решения рациональных уравнений:

Система для решения дробно рациональных уравнений:

Что такое рациональные уравнения?

Давай научимся отличать рациональные уравнения от иррациональных! Зачем? Рациональные уравнения решать проще.

А зачем работать больше, если можно работать меньше?

Надеюсь, теперь ты сможешь различать, к какому виду относится уравнение. (И не поедешь из Москвы в Петербург через Магадан, решая рациональные уравнения как нерациональные).

Целые рациональные уравнения

Важно знать, что рациональные уравнения в свою очередь тоже разные бывают.

Если в дроби нет деления на переменную (то есть на \( \displaystyle x\), \( \displaystyle y\) и т.д.), тогда рациональное уравнение будет называться целым (или линейным) уравнением, вот примеры:

Умеешь такие решать? – конечно, умеешь, упрощаешь и находишь неизвестное, тема-то 5-ого или 6-ого класса.

Ну, рассмотрим первый из примеров на всякий случай и по порядочку. Все неизвестные переносим влево, все известные вправо:

Какой наименьший общий знаменатель будет?

Правильно \( \displaystyle 6\)!

Чтоб к нему привести домножаем и числитель и знаменатель первого слагаемое на \( \displaystyle 2\), а второго на \( \displaystyle 3\), этого делать не запрещено, если и числитель и знаменатель дроби умножить на одно и то же значение, то дробь от этого не изменится, т.к. ее можно будет сократить на то же число.

А \( \displaystyle 13\) не трогаем, оно нам не мешает, имеем:

А теперь делим обе части на \( \displaystyle 13\):

Поскольку уравнение целое, что мы уже определили, то и ограничений никаких нет, \( \displaystyle 6\), так \( \displaystyle 6\), ну можно для верности подставить этот ответ в исходное уравнение, получим \( \displaystyle 0=0\), значит все верно и ответ подходит (ты можешь пересчитать, а вообще должно сойтись).

Дробно-рациональные уравнения

А вот еще одно уравнение \( \displaystyle \frac<5>+\frac<4-6><(x+1)\cdot (x+3)>=3\).

Это уравнение целое? НЕТ. Тут есть деление на переменную \( \displaystyle x\), а это говорит о том, что уравнение не целое. Тогда какое же оно? Это дробно рациональное уравнение.

Дробно-рациональное уравнение – рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.

На первый взгляд особой разницы не видно, ну давай попробуем решать его как мы решали целое (линейное) уравнение.

Для начала найдем наименьший общий знаменатель, это будет \( \displaystyle (x+1)\cdot (x+3)\).

Важный момент!

В предыдущем примере, где было целое уравнение мы не стали свободный член \( \displaystyle 13\) приводить к знаменателю, т.к. умножали все на числа без переменных, но тут-то наименьший общий знаменатель \( \displaystyle (x+1)\cdot (x+3)\).

А это тебе не шутки, переменная в знаменателе!

Решая дробно-рациональное уравнение, обе его части умножаем на наименьший общий знаменатель!

Это надеюсь, ты запомнишь, но давай посмотрим что вышло:

Что-то оно огромное получилось, надо все посокращать:

\( \displaystyle 5(x+3)+(4-6)=3\cdot (x+1)\cdot (x+3)\).

Раскроем скобки и приведем подобные члены:

Ну как, это уже попроще выглядит, чем в начале было?

Выносим за скобку общий множитель: \( \displaystyle 3x\cdot (x+1)=0\)

У этого уравнения два решения, его левая сторона принимает нулевое значение при \( \displaystyle x=0\) и \( \displaystyle x=-1\).

Вроде бы все, ну ладно давайте напоследок подставим корни \( \displaystyle x=0\) и \( \displaystyle x=-1\) в исходное уравнение, чтобы проверить, нет ли ошибок. Сначала подставим \( \displaystyle 0\), получается \( \displaystyle 3=3\) –нет претензий?

Но ведь это же будет ноль!

На ноль делить нельзя, это все знают, в чем же дело.

Дело в ОДЗ — Области Допустимых Значений!

Всякий раз когда ты видишь уравнение, где есть переменные (\( \displaystyle x,y\) и т.д.) в знаменателе, прежде всего, нужно найти ОДЗ, найти какие значения может принимать икс.

Хотя удобнее в ОДЗ написать, чему икс НЕ может быть равен, ведь таких значений не так много, как правило.

Просто запомни, что на ноль делить нельзя! И перед тем как решать наше уравнение нам следовало сделать так:

Если бы мы сразу так написали, то заранее бы знали, что эти ответы стоит исключить и так, из полученных нами \( \displaystyle x=0\) и \( \displaystyle x=-1\) мы смело исключаем \( \displaystyle x=-1\), т.к. он противоречит ОДЗ.

Значит, какой ответ будет у решенного уравнения?

В ответ стоит написать только один корень, \( \displaystyle x=0\).

Стоит заметить, что ОДЗ не всегда сказывается на ответе, возможны случаи, когда корни, которые мы получили, не попадают под ограничения ОДЗ.

Но писать ОДЗ в дробно рациональных уравнениях стоит всегда – так просто спокойнее, что ты ничего не упустил и да,

ВСЕГДА по окончании решения сверяй свои корни и область допустимых значений!

Алгоритм решения рационального уравнения

Усвоил, говоришь? А ты докажи! 🙂 Вот тебе примеры на закрепление. Попробуй решить сам, а потом сверься с ответом.

Источник

Целое уравнение и его корни

Урок 11. Алгебра 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Целое уравнение и его корни»

Отличие целого уравнения от дробно-рационального заключается в том, что областью определения целого уравнения является множество всех действительных чисел. То есть аргумент может принимать любые значения.

Среди уравнений найдем те, которые являются целыми уравнениями с одной переменной.

Целыми будут следующие уравнения.

Каждое из этих уравнений можно преобразовать.

Во втором уравнении:

В третьем уравнении:

Рассмотрим пример: определить степень уравнений.

Причём, во всех этих случаях, a≠0.

Данное уравнение имеет три корня.

Рассмотрим пример: решить уравнение.

Так как для него трудно найти способ решения, будем работать с исходной записью. Введём замену.

Получим новое уравнение, решим его:

Алгоритм решения биквадратного уравнения:

1. Ввести новую переменную .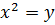

2. Решить уравнение 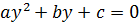, полученное после подстановки новой переменной.

3. Выполняю обратную подстановку .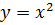

4. Найти корни исходного биквадратного уравнения.

Приведем его к биквадратному уравнению:

Введём новую переменную и выполним подстановку:

Источник

Конспект урока целые уравнения

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Урок алгебры в 9 классе

Тема урока: «Целые уравнения»

Урок алгебры в 9 классе

Тема урока: «Целые уравнения»

2 .Развивающие : развивать умения в применении знаний в конкретной ситуации; логическое мышление, умение работать в проблемной ситуации; умение обобщать, конкретизировать, правильно излагать мысли; развивать самостоятельную деятельность учащихся.

3. Воспитательные: воспитывать интерес к предмету через содержание учебного материала; умение работать в коллективе, взаимопомощь, культуру общения, умение применять преемственность в изучении отдельных тем; воспитывать настойчивость в достижении цели, умение не растеряться в проблемных ситуациях

Оборудование: ПК, мультимедийные проектор, интерактивная доска, пульты

Приложение: Презентация к уроку в программе PowerPoint

I. Организационный момент. Сообщение темы, целей урока.

Повторение: 1) целое выражение и его степень (привести примеры). ПК, мультимедийные проектор

7)

9)

10)

11)

Привести примеры дробных выражений. Указать степень многочлена.

2) 1) Что такое уравнение? (Равенство, содержащее переменную, называется уравнением с одной переменной)

2) Что такое корни уравнения? (Значение переменной, при котором уравнение обращается в верное числовое равенство )

Что значит решить уравнение? (Найти все его корни или доказать, что корней нет)

III. Объяснение нового материала

1)Определение целого уравнения.

Уравнения, в которых левая и правая часть являются целыми выражениями, называются целыми уравнениями.

2) Определите степень уравнения: Уравнения бывают 1, 2, 3, 4, и более высоких степеней. Мы с вами большей частью решаем уравнение I, II, III IV степени.

Всякое уравнение можно заменить равносильным ему уравнением, левая часть которого – многочлен стандартного вида, а правая – нуль.

Если уравнение с одной переменной записано в виде P(x) = 0, где P(x)- многочлен стандартного вида, то степень этого многочлена называют степенью данного уравнения

Всякое уравнение можно заменить равносильным ему уравнением, левая часть которого – многочлен стандартного вида, а правая – нуль.

Степенью произвольного целого уравнения называют степень равносильного ему уравнения вида Р(х)=0, где Р(х)- многочлен стандартного вида

Закрепление понятия степени уравнения

Укажите степень уравнения

(выполняют устно, при необходимости записать в тетрадь № 5,9,10)

1) x 2 = 0 6) x 2 –16 = 0

2) x 3 – 25x = 0 7) x 4 – 3x 2 = 0

3) 9x –27 = 0 8) x 2 = – 49

4) 10 – х 2 = 26х 9) x(x – 1)(x + 4) = 0

3)Примеры решения уравнений различных степеней:

Решите уравнения: (1чел. с каждого ряда, на месте 1 ряд 1 уравнение, 2 ряд- 2 уравнение, 3 ряд- 3 уравнение)

D =1, D >0, D =-12, D D =0,1 корень

Сколько корней может иметь уравнение 2 степени (квадратное)? Не более двух!

Динамическая пауза. ПК, проектор, гимнастика для глаз.

IV . Закрепление изученного материала.

Решение уравнений, применяя разложение на множители.

Пример 1: Вынесение множителя за скобки.

Разложение на множители способом группировки.

Решить № 267 (б) рассмотреть 2 способа решения: умножение на общий знаменатель и с помощью пропорции.

Вопросы учащимся: Какое уравнение называется целым? Как найти степень целого уравнения? Сколько корней имеет целое уравнение в зависимости от степени уравнения?

Обучающая самостоятельная работа.

(Работа с пультами, программа Mimio Studio )

Определить степень уравнения (ученики указывают степень уравнения пользуясь пультами)

Вариант 1 Вариант 2

2) x (x – 1)= 0 2) 2 x (x + 7) = 0

1) 2 2) 2 3) 3 4) 3 5) 2 6) 3 7) 4 8) 5

Результаты работы (в процентах высвечиваются на доске), анализ ошибок.

Домашнее задание : п.12(пример 1-2) решить № 265, 266(а),272 (а,в,д,)

Источник

Целое уравнение и его корни

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Тема урока. Целое уравнение и его корни.

Цели урока: обобщить сведения об уравнениях, вспомнить понятие целого уравнения, вспомнить понятие степени уравнения, продолжить формирование навыков решения уравнений.

Задания №1. Соотнесите простейшие целые уравнения и ответы:

ЦЕЛЫМ УРАВНЕНИЕМ С ОДНОЙ ПЕРЕМЕННОЙ НАЗЫВАЕТСЯ УРАВНЕНИЕ, ЛЕВАЯ И ПРАВАЯ ЧАСТИ КОТОРОГО- ЦЕЛЫЕ ВЫРАЖЕНИЯ

Если уравнение с одной переменной записано в виде P(x) = 0, где P(x)- многочлен стандартного вида, то степень этого многочлена называют степенью данного уравнения Например:

Задание №2. Определите степени следующих уравнений:

Задание №3. Найдите корни уравнения

Методы решения уравнений графический введение новой переменной разложение на множители вынесение за скобку общего множителя формулы сокращенного умножения способ группировки Делением многочлена на многочлен

Задание №4. Какую подстановку необходимо выполнить, чтобы уравнение стало квадратным? а) х4 +2х2 + 1 = 0; д) х6 – 3х3 + 2 = 0; е) у8 – 4 = 0.

Задание №5. Решите уравнение

Замечание 2 Из рассмотренных примеров видно, что биквадратное уравнение может иметь четыре, три, два, один действительный корень, но может и не иметь корней.

Задание №6. Решите уравнение 1 2

Д/З: в дневник.ру переходим по ссылке на интерактивную рабочую тетрадь.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1561208

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Учителям истории предлагают предоставить право бесплатно посещать музеи

Время чтения: 2 минуты

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

В Оренбурге школьников переведут на дистанционное обучение с 9 декабря

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Минпросвещения намерено расширить программу ускоренного обучения рабочим профессиям

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник