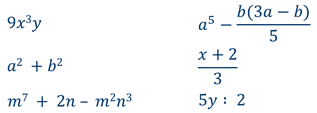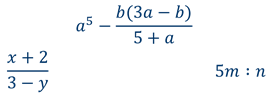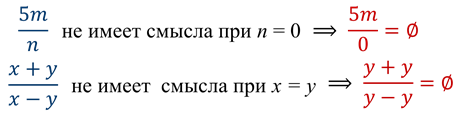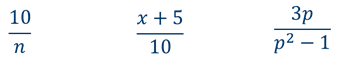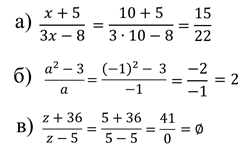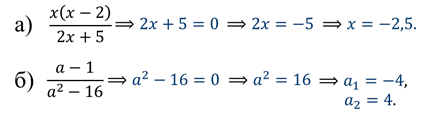Что такое целое выражение в алгебре
Преобразование целых выражений.
Данная статья посвящена одному из видов выражений курса алгебры – целым выражениям, а также их преобразованию. Сначала дадим определение целых выражений. Дальше покажем, какие тождественные преобразования наиболее часто выполняются с ними. Наконец, покажем, что любое целое выражение можно преобразовать в многочлен, и на примерах разберем, как это преобразование проводится и на чем оно основано.
Навигация по странице.
Определение и примеры целых выражений
Изучение целых выражений входит в программу курса алгебры для 7 классов. На уроках алгебры и дается следующее определение целых выражений.
Целыми выражениями называют числа, переменные, а также всевозможные выражения, составленные из них при помощи действий сложения, вычитания и умножения (произведение одинаковых множителей может быть записано и в виде степени с натуральным показателем), которые также могут содержать скобки и деление на отличное от нуля число.
К слову, любой многочлен, как и любой одночлен, являются целыми выражениями.
Следует отметить, что в школе мы работаем преимущественно с такими целыми выражениями, которые если содержат в своей записи числа, то эти числа рациональные (в частности, целые или натуральные). Иными словами, изучаемые в школе целые выражения не содержат в своей записи иррациональных чисел. Их еще называют целыми рациональными выражениями.
Какие преобразования целых выражений возможны?
С целыми выражениями можно выполнять все основные тождественные преобразования, такие как раскрытие скобок, группировка слагаемых и множителей, приведение подобных слагаемых и т.п. Рассмотрим решения нескольких примеров.
Преобразуйте целое выражение 

Представьте целое выражение 6·x 2 ·y+18·x·y−6·y−(x 2 +3·x−1)·(x 3 +4·x) в виде произведения двух многочленов.
Напомним, что при выполнении тождественных преобразований выражений, в том числе и целых, нужно соблюдать порядок выполнения действий.
Преобразование в многочлен
Во многих случаях преобразования целых выражений проводятся с единственной целью – представить их в виде многочленов. Вообще, любое целое выражение можно представить в виде многочлена. Это утверждение следует из определения целого выражения, которое мы дали выше, а также из того, как мы определены действия с многочленами и одночленами. Действительно, всякое целое выражение мы можем рассматривать как соединенные знаками действий многочлены, а мы знаем, что умножение многочленов, как и их сложение и вычитание в результате дает многочлен.
Чтобы целое выражение представить в виде многочлена, надо выполнить все действия с многочленами, одночленами и числами, составляющими это выражение, согласно принятому порядку выполнения действий.
Исходное целое выражение содержит и скобки, и возведение в степень, и действия разных ступеней.
Понятно, что при выполнении умножения многочленов и возведении их в степень по возможности следует пользоваться формулами сокращенного умножения, что ускорит процесс преобразования. Например, в предыдущем примере возведение многочлена 2·x−1 в квадрат было целесообразно проводить с использованием формулы квадрата разности. Да и вообще, любые действия желательно выполнять максимально рационально.
В заключение этой статьи отметим, что процесс преобразования в многочлен будет намного короче, если предварительно все составляющие исходное целое выражение одночлены и многочлены привести к стандартному виду.
Презентация по алгебре на тему «Целые выражения»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Описание слайда:
Описание слайда:
Любой многочлен, как и любой одночлен, являются целыми выражениями.
Любое целое выражение можно преобразовать в многочлен стандартного вида.
Целым выражением называют числа, переменные, а также всевозможные выражения, составленные из них при помощи действий сложения, вычитания и умножения.
Числа 9, 0, −12, 7/11, и др., переменные a, b, c, x и т.п. можно считать целыми выражениями.
Их разнообразные суммы, разности и произведения будут также давать целые выражения, например, x+1, 5·y−2·y−3, 3+x·z
Описание слайда:
ЦЕЛЫМ ВЫРАЖЕНИЕМ называют числа, переменные, а также всевозможные выражения, составленные из них при помощи действий сложения, вычитания и умножения.
Выражение x:5+5:x не является целым, так как содержит деление на переменную x.
не является целым, так как содержит деление на выражение с переменными.
Описание слайда:
ВОПРОС: Какие из данных выражений не являются целыми?
7ab2c, 15, ab, (1/4)x, 5/(a+d), y+5
Описание слайда:
№328 Вычислить значение выражения
а) (a+b+c)(a2+b2), a=-3, b=-2, c=4
б) (a+b-c)(a2-b2), a=3, b=2, c=-4
в) (0,1-x)(0,1+y)(0,1+z), x=2, y=-1, z=2
г) (x+0,1y)(0,1x+y)(0,1x+y), x=-2, y=1
д) (1/2-x)(1/2-x)(1/2-x), x=4
е) ((1/3)p+(1/2)q)((1/3)p+(1/2)q)((1/3)p+(1/2)q), p=9, q=-1
ж) (1+x)(x+2)(3+x)(x+4), x=-1/3
Описание слайда:
Описание слайда:
№329 Вычислить значение выражения
Описание слайда:
Описание слайда:
Преобразуйте выражение в многочлен стандартного вида и определите его степень:
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Презентация по алгебре на тему «Тождественные равенства целых выражений»
Презентация по алгебре на тему «Умножение одночленов и многочленов»
Контрольная работа по теме «Случайные события. Вероятность событий»»
Конспект урока на тему «Свойства действий над числами»
Видеоролик: » Решение систем уравнений методом подстановки» (7класс)
Методическая разработка по математике для 8 класса «Взаимное расположение окружностей»
Видеоролик: » Решение задач с помощью линейных уравнений» (7класс)
Видеоролик : «Решение задач с пощью систем уравнений» (8 кл)
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5376676 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
До конца 2024 года в РФ построят около 1 300 школ
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
МГУ откроет первую в России магистерскую программу по биоэтике
Время чтения: 2 минуты
ВПР для школьников в 2022 году пройдут весной
Время чтения: 1 минута
Более 50 российских школ перешли на дистанционку из-за коронавируса
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Преобразование целых выражений
Благодаря курсу алгебры, известно, что все выражения требуют преобразования для более удобного решения. Определение целых выражений способствует тому, что для начала выполняются тождественные преобразования. Будем преобразовывать выражение в многочлен. В заключении разберем несколько примеров.
Определение и примеры целых выражений
Целые выражения – это числа, переменные или выражения со сложением или вычитанием, которые записываются в виде степени с натуральным показателем, которые также имеют скобки или деление, отличное от нуля.
Многочлен и одночлен являются целыми выражениями, с которыми встречаемся в школе при работе с рациональными числами. Иначе говоря, целые выражения не включают в себя записи иррациональных дробей. Другое название – это целые иррациональные выражения.
Какие преобразования целых выражений возможны?
Целые выражения рассматриваются при решении как основные тождественные преобразования, раскрытие скобок, группирование, приведение подобных.
Для начала необходимо применить правило раскрытия скобок. Получим выражение вида 2 · ( a 3 + 3 · a · b − 2 · a ) − 2 · a 3 − ( 5 · a · b − 6 · a + b ) = = 2 · a 3 + 2 · 3 · a · b + 2 · ( − 2 · a ) − 2 · a 3 − 5 · a · b + 6 · a − b = = 2 · a 3 + 6 · a · b − 4 · a − 2 · a 3 − 5 · a · b + 6 · a − b
После чего можем привести подобные слагаемые:
Представить выражение 6 · x 2 · y + 18 · x · y − 6 · y − ( x 2 + 3 · x − 1 ) · ( x 3 + 4 · x ) в виде произведения.
6 · y · ( x 2 + 3 · x − 1 ) − ( x 2 + 3 · x − 1 ) · ( x 3 + 4 · x ) = = ( x 2 + 3 · x − 1 ) · ( 6 · y − ( x 3 + 4 · x ) )
Ответ: 6 · x 2 · y + 18 · x · y − 6 · y − ( x 2 + 3 · x − 1 ) · ( x 3 + 4 · x ) = = ( x 2 + 3 · x − 1 ) · ( 6 · y − x 3 − 4 · x )
Тождественные преобразования требуют строгое выполнение порядка действий.
8 · x 8 + 4 · x : 8 = 8 · x 8 + 4 · x · 1 8 = 8 · x 8 + 4 · 1 8 · x = 8 · x 8 + 1 2 · x
Преобразование в многочлен
Большинство случаев преобразования целых выражений – это представление в виде многочлена. Любое выражение можно представить в виде многочлена. Любое выражение может быть рассмотрено как многочлены, соединенные арифметическими знаками. Любое действие над многочленами в итоге дает многочлен.
Для того, чтобы выражение было представлено в виде многочлена, необходимо выполнять все действия с многочленами, согласно алгоритму.
Разберем умножение. Видно, что 2 · ( 2 · x 3 − 1 ) = 4 · x 3 − 2 и ( 4 · x 2 − 4 · x + 1 ) · ( 3 − x ) = 12 · x 2 − 4 · x 3 − 12 · x + 4 · x 2 + 3 − x = = 16 · x 2 − 4 · x 3 − 13 · x + 3
Выполняем сложение, после чего придем к выражению:
Умножение и возведение в степень многочлена говорит о том, что необходимо использовать формулы сокращенного умножения для ускорения процесса преобразования. Это способствует тому, что действия будут выполнены рационально и правильно.
Чтобы преобразование не было слишком длинным, необходимо заданное выражение приводить к стандартному виду.
Упростить выражение вида ( 2 · a · ( − 3 ) · a 2 · b ) · ( 2 · a + 5 · b 2 ) + a · b · ( a 2 + 1 + a 2 ) · ( 6 · a + 15 · b 2 ) + ( 5 · a · b · ( − 3 ) · b 2 )
− 6 · a 3 · b · ( 2 · a + 5 · b 2 ) + a · b · ( 2 · a 2 + 1 ) · ( 6 · a + 15 · b 2 ) − 15 · a · b 3 = = − 12 · a 4 · b − 30 · a 3 · b 3 + ( 2 · a 3 · b + a · b ) · ( 6 · a + 15 · b 2 ) − 15 · a · b 3 = = − 12 · a 4 · b − 30 · a 3 · b 3 + 12 · a 4 · b + 30 · a 3 · b 3 + 6 · a 2 · b + 15 · a · b 3 − 15 · a · b 3 = = ( − 12 · a 4 · b + 12 · a 4 · b ) + ( − 30 · a 3 · b 3 + 30 · a 3 · b 3 ) + 6 · a 2 · b + ( 15 · a · b 3 − 15 · a · b 3 ) = 6 · a 2 · b
Ответ: ( 2 · a · ( − 3 ) · a 2 · b ) · ( 2 · a + 5 · b 2 ) + a · b · ( a 2 + 1 + a 2 ) · ( 6 · a + 15 · b 2 ) + + ( 5 · a · b · ( − 3 ) · b 2 ) = 6 · a 2 · b
Рациональные выражения
Урок 1. Алгебра 8 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Рациональные выражения»
На этом уроке мы вспомним, какие выражения называют целыми и дробными. Познакомимся с рациональными выражениями. Узнаем, какие значения называют допустимыми. А также научимся находить допустимые значения выражения.
Вы уже знакомы с целыми и дробными выражениями. Давайте вспомним их определения.
Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.
В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.
Целые и дробные выражения называют рациональными выражениями.
Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.
Напомним, что целые выражения имеют смысл при любых значениях переменных. Чтобы найти значение целого выражения, нужно подставить указанное значение переменной и выполнить все действия.
Дробное выражение при некоторых значениях переменных может не иметь смысла.
Чтобы найти значение рационального выражения, надо:
1) подставить числовое значение переменной в данное выражение;
2) выполнить все действия.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Множество всех допустимых значений переменных называется областью допустимых значений (коротко ОДЗ) или областью определения выражения.
Как вы уже знаете, выражение вида 
Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.
Найдите значение дроби.
Найдите допустимые значения переменной в выражениях:
Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.
В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.
Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.
Чтобы найти значение рационального выражения, надо:
1) Подставить числовое значение переменной в данное выражение;
2) Выполнить все действия.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Множество всех допустимых значений переменных называется областью допустимых значений или областью определения выражения.
Основные виды выражений в алгебре
Уроки алгебры знакомят нас с различными видами выражений. По мере поступления нового материала выражения усложняются. При знакомстве со степенями они постепенно добавляются в выражение, усложняя его. Также происходит с дробями и другими выражениями.
Чтобы изучение материала было максимально удобным, это производится по определенным названиям для того, чтобы можно было их выделить. Данная статья даст полный обзор всех основных школьных алгебраических выражений.
Одночлены и многочлены
Выражения одночлены и многочлены изучаются в школьной программе, начиная с 7 класса. В учебники были даны определения такого вида.
Одночлены – это числа, переменные, их степени с натуральным показателем, любые произведения, сделанные с их помощью.
Многочленами называют сумму одночленов.
Чтобы отличать одночлен от многочлена, обращают внимание на степени и их определения. Немаловажно понятие коэффициента. При приведении подобных слагаемых их разделяют на свободный член многочлена или старший коэффициент.
Над одночленами и многочленами чаще всего выполняются какие-то действия, после которых выражение приводится к вижу одночлена. Выполняется сложение, вычитание, умножение и деление, опираясь на алгоритм для выполнения действий с многочленами.
Когда имеется одна переменная, не исключено деление многочлена на многочлен, которые представляются в виде произведения. Такое действие получило название разложение многочлена на множители.
Рациональные (алгебраические) дроби
Понятие рациональные дроби изучаются в 8 классе средней школы. Некоторые авторы называют их алгебраическими дробями.
Рациональной алгебраической дробью называют дробь, в которой на месте числителя и знаменателя выступают многочлены или одночлены, числа.
Алгебраические дроби можно складывать, вычитать, умножать, делить, возводить в степень. Подробнее это рассматривается в разделе действий с алгебраическими дробями. Если необходимо преобразовать дробь, нередко пользуются свойством сокращения и приведения к общему знаменателю.
Рациональные выражения
В школьном курсе изучается понятие иррациональных дробей, так как необходима работа с рациональными выражениями.
Рациональные выражения считаются числовыми и буквенными выражениями, где используются рациональные числа и буквы со сложением, вычитанием, умножением, делением, возведением в целую степень.
Рациональные выражения могут не иметь знаков, принадлежащих функции, которые приводят к иррациональности. Рациональные выражения не содержат корней, степеней с дробными иррациональными показателями, степеней с переменными в показателе, логарифмических выражений, тригонометрических функций и так далее.
Все рациональные выражения подразделяют на целые и дробные.
Целые рациональные выражения
Целые рациональные выражения – это такие выражения, не содержащие деления на выражения с переменными отрицательной степени.
Дробные рациональные выражения
Дробное рациональное выражение – это выражение, которое содержит деление на выражение с переменными отрицательной степени.
Выражения со степенями
Выражения, которые содержат степени в любой части записи, называют выражениями со степенями или степенными выражениями.
Иррациональные выражения, выражения с корнями
Корень, имеющий место быть в выражении, дает ему иное название. Их называют иррациональными.
Иррациональными выражениями называют выражения, которые имеют в записи знаки корней.
Тригонометрические выражения
Для работы с такими функциями необходимо пользоваться свойствами, основными формулами прямых и обратных функций. Статья преобразование тригонометрических функций раскроет этот вопрос подробней.
Логарифмические выражения
После знакомства с логарифмами можно говорить о сложных логарифмических выражениях.
Выражения, которые имеют логарифмы, называют логарифмическими.
Для углубления изучения материала, следует обратиться к материалу о преобразовании логарифмических выражений.
Дроби
Существуют выражения особого вида, которые получили название дроби. Так как они имеют числитель и знаменатель, то они могут содержать не просто числовые значения, а также выражения любого типа. Рассмотрим определение дроби.
Дробью называют такое выражение, имеющее числитель и знаменатель, в которых имеются как числовые, так и буквенные обозначения или выражения.
Выражение общего вида
Их вид говорит о том, что можно отнести к любому из вышеперечисленных видов. Чаще всего их не относят ни к какому, так как они имеют специфичное комбинированное решение. Их рассматривают как выражения общего вида, причем для описания не используются дополнительные уточнения или выражения.
При решении такого алгебраического выражения всегда необходимо обращать внимание на его запись, наличие дроби, степеней или дополнительных выражений. Это нужно для того, чтобы точно определиться со способом его решения. Если нет уверенности в его названии, то рекомендуется называть его выражением общего типа и решать, согласно выше написанному алгоритму.