что такое свойство фигур в математике 2 класс

Основные геометрические фигуры

Основные понятия

Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.

Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.

Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.

Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

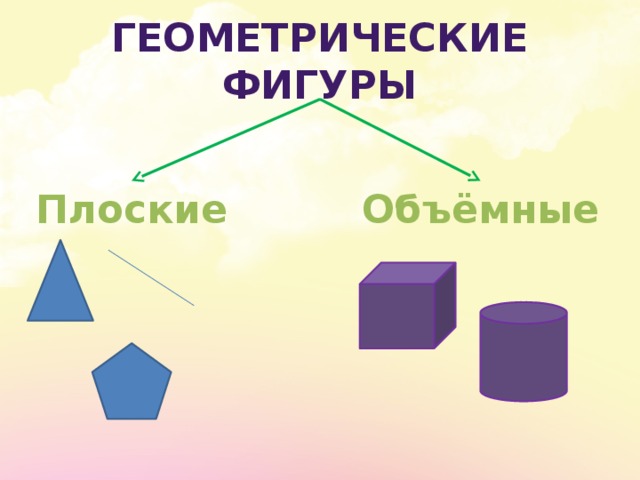
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Если все точки фигуры принадлежат одной плоскости, значит она является плоской.

Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.

Примеры объемных геометрических фигур:

Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.

Прямоугольник

Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом.

Узнать площадь прямоугольника помогут следующие формулы:

Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.

Периметр прямоугольника — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Квадрат

Квадрат — это тот же прямоугольник, у которого все стороны равны.

Найти площадь квадрата легко:

Периметр квадрата — это длина стороны, умноженная на четыре.

P = 4 × a, где a — длина стороны.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны

Ромб — это параллелограмм с равными сторонами.

Общие формулы расчета площади фигур:

Периметр ромба — это произведение длины стороны на четыре.

P = 4 × a, где a — длина стороны.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

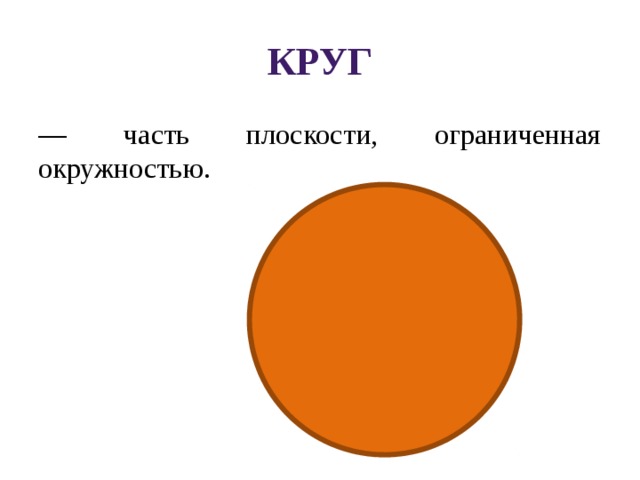
Круг — это множество точек на плоскости, которые удалены от центра на равном радиусу расстоянии.

Окружность — это граница круга.

Радиус окружности — это расстояние от центра окружности до любой точки на ней.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Источник

Геометрические фигуры, 2 класс

Данная презентация предназначина для повтрения геометрических фигур, их видов

Содержимое разработки

— это эталон*, с помощью которого можно определить форму предмета или его частей.

* 1. точная мера или точный измерительный прибор, служащие для воспроизведения, хранения и передачи единицы измерения какой-либо величины. 2. перен. мерило, образец для подражания, сравнения.

— это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса.

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать

— это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет.

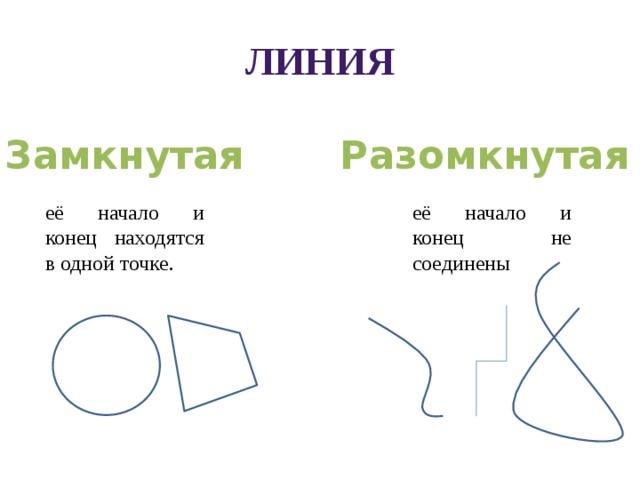
её начало и конец находятся в одной точке.

её начало и конец не соединены

— это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны.

— это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону.

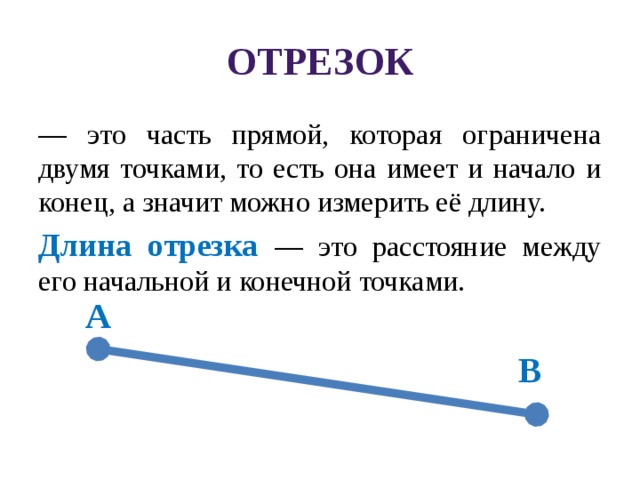
— это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.

Длина отрезка — это расстояние между его начальной и конечной точками.

— замкнутая плоская кривая

— часть плоскости, ограниченная окружностью.

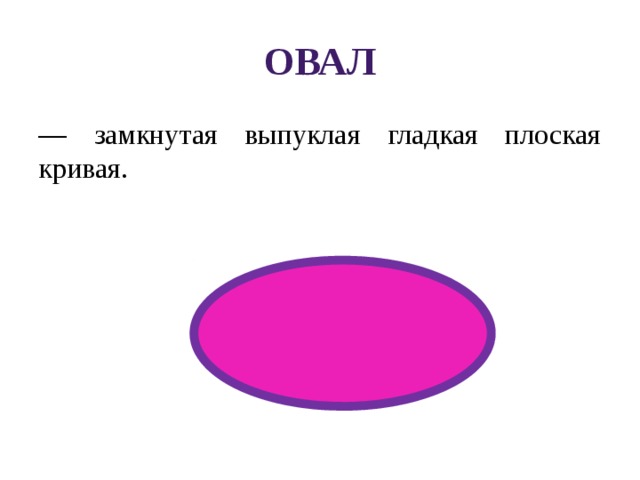
— замкнутая выпуклая гладкая плоская кривая.

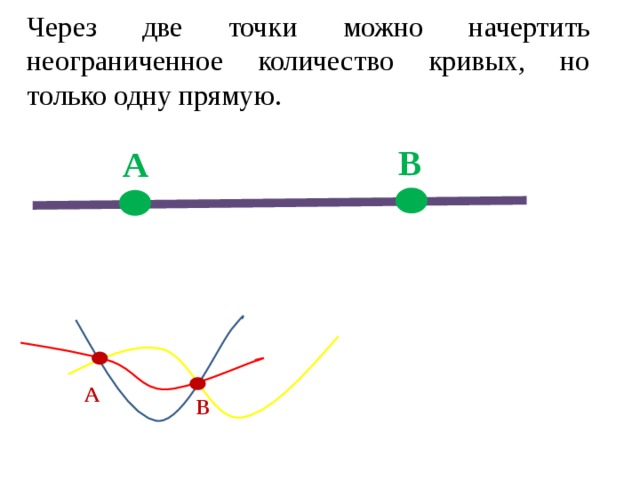
Через две точки можно начертить неограниченное количество кривых, но только одну прямую.

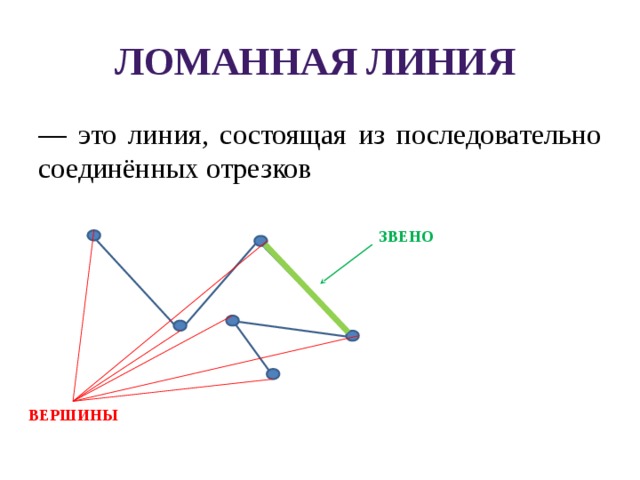
— это линия, состоящая из последовательно соединённых отрезков

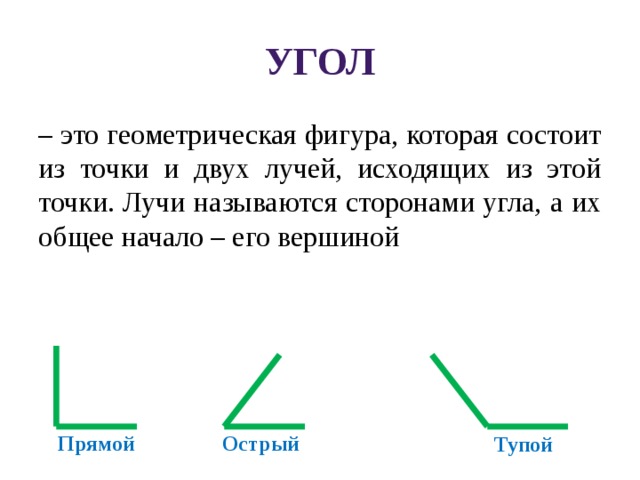
– это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало – его вершиной

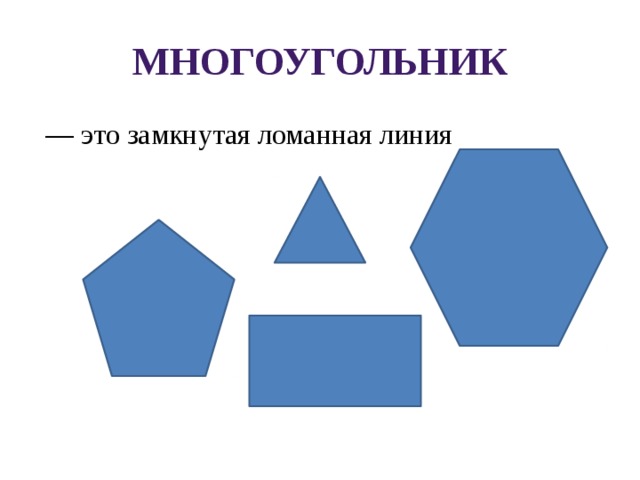
— это замкнутая ломанная линия

— геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков.

— это фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков, причем никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Точки называются вершинами четырехугольника, а соединяющие их отрезки – сторонами.

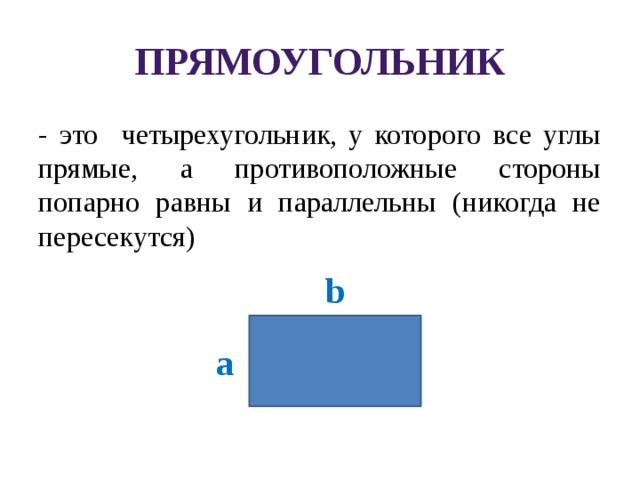
— это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны и параллельны (никогда не пересекутся)

— это четырехугольник, у которого все углы прямые и все стороны равны.

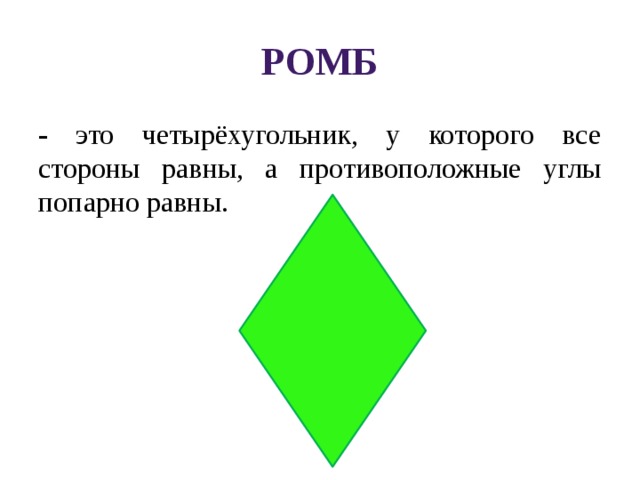
— это четырёхугольник, у которого все стороны равны, а противоположные углы попарно равны.

Источник

Урок математики для 2 класса «Геометрические фигуры и их свойства»

Геометрические фигуры и их свойства

Цели: учить чертить два отрезка, которые пересекаются под прямым углом; формировать умение строить тупоугольный (остроугольный, прямоугольный) треугольник; строить треугольник по данной стороне и высоте, проведенной к этой стороне; определять вид треугольника.

1. Рассмотрите рисунки. Назовите геометрическую фигуру, которую можно увидеть в каждом предмете.

2. Найдите длину гусеницы, используя длину радиуса каждой окружности.

– Из каких фигур состоит гусеница?

II. Работа по учебнику.

Задание 369. Какой треугольник называется остроугольным? Постройте остроугольный треугольник, у которого одна из сторон имеет длину 10 см. Сколько острых углов у остроугольного треугольника?

Задание 370. Какой треугольник называется тупоугольным? Постройте тупоугольный треугольник, у которого одна из сторон имеет длину 10 см.

– Сколько острых углов у тупоугольного треугольника?

Задание 371. Какой треугольник называется прямоугольным? Постройте прямоугольный треугольник, у которого одна из сторон имеет длину 10 см.

– Сколько острых углов у прямоугольного треугольника?

Задание 372. Постройте треугольник, у которого одна сторона имеет длину 8 см, а высота, проведенная к этой стороне, имеет длину 4 см.

Задание 373. Что общего у всех данных треугольников? (Основание треугольников равно диаметру окружности.) Определите вид каждого треугольника. (Прямоугольный разносторонний и прямоугольный равнобедренный.) Чем является бoльшая сторона каждого треугольника для окружности? (Диаметром.) Начертите прямоугольный треугольник, у которого бoльшая сторона имеет длину 4 см.

III. Самостоятельная работа (задание на доске).

– Вычислите числовое значение площади и периметра данных прямоугольников, если от них осталась такая часть:

Фронтальная проверка. Объясните, что обозначают выражения:

7 ∙ 10; 10 ∙ 4; 8 ∙ 2; (7 + 10) ∙ 2; (10 + 4) ∙ 2; (8 + 2) ∙ 2.

– Назовите виды треугольников.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Скоростное чтение

Курс повышения квалификации

Специфика преподавания предмета «Родной (русский) язык» с учетом реализации ФГОС НОО

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Краткое описание документа:

Геометрические фигуры и их свойства Цели: учить чертить два отрезка, которые пересекаются под прямым углом; формировать умение строить тупоугольный (остроугольный, прямоугольный) треугольник; строить треугольник по данной стороне и высоте, проведенной к этой стороне; определять вид треугольника. Ход урока I. Устный счет. 1. Рассмотрите рисунки. Назовите геометрическую фигуру, которую можно увидеть в каждом предмете. 2. Найдите длину гусеницы, используя длину радиуса каждой окружности. – Из каких фигур состоит гусеница? II. Работа по учебнику. Задание 369. Какой треугольник называется остроугольным? Постройте остроугольный треугольник, у которого одна из сторон имеет длину 10 см. Сколько острых углов у остроугольного треугольника? Задание 370. Какой треугольник называется тупоугольным? Постройте тупоугольный треугольник, у которого одна из сторон имеет длину 10 см. – Сколько острых углов у тупоугольного треугольника? Задание 371. Какой треугольник называется прямоугольным? Постройте прямоугольный треугольник, у которого одна из сторон имеет длину 10 см. – Сколько острых углов у прямоугольного треугольника? Задание 372. Постройте треугольник, у которого одна сторона имеет длину 8 см, а высота, проведенная к этой стороне, имеет длину 4 см. Задание 373. Что общего у всех данных треугольников? (Основание треугольников равно диаметру окружности.) Определите вид каждого треугольника. (Прямоугольный разносторонний и прямоугольный равнобедренный.) Чем является бoльшая сторона каждого треугольника для окружности? (Диаметром.) Начертите прямоугольный треугольник, у которого бoльшая сторона имеет длину 4 см. III. Самостоятельная работа (задание на доске). – Вычислите числовое значение площади и периметра данных прямоугольников, если от них осталась такая часть: Фронтальная проверка. Объясните, что обозначают выражения: 7 ∙ 10; 10 ∙ 4; 8 ∙ 2; (7 + 10) ∙ 2; (10 + 4) ∙ 2; (8 + 2) ∙ 2. IV. Итог урока. – Назовите виды треугольников.

Источник

Урок математики во 2 классе «Геометрические фигуры и их свойства»

Тема: геометрические фигуры и их свойства.

Цель: формировать понятие «геометрическая фигура», «свойства фигур», развивать умение наблюдать и сравнивать, воспитывать любознательность

Орг. момент. Вступительная беседа учителя.

Сообщение темы урока:

Сегодня мы совершим путешествие в одну необычную, но знакомую нам математическую страну. Мы повстречаемся с жителями этой страны (на уроках математики мы с некоторыми из них уже познакомились). А что может быть лучше, чем встреча старых приятелей?

Просьба к вам, путешественники, прихватить с собой внимание, наблюдательность, смекалку, чтобы справиться с заданиями, которые встретятся на нашем пути. А все записи о путешествии будем вести в личном дневнике, т.е. в рабочей тетради. Итак, первая запись, историческая дата нашего путешествия. Дети записывают число, классная работа.

Как же называется страна,

Куда мы держим путь?

Ты букву напиши вместо числа,

На сколько 45 больше 43? (на 2).

Уменьшаемое 53, вычитаемое 41. Найди разность. (12)

25 уменьшить на 21 (4).

На сколько 9 меньше 11. (на 2)

Чему равна сумма двух восьмёрок? (16)

Какое число на 7 меньше 13? (6)

Какое число больше 0 на 20? (20)

Читаем хором название страны, где ждут нас с нетерпением.

Прежде чем мы двинемся дальше, ещё раз внимательно посмотрите на числа, которые помогли нам. Делаем очередную запись в нашем дневнике путешествия.

№ 2. Работа с числами.

а) найди закономерность расположения чисел, продолжи ряд пятью своими числами составь свой ряд

б) сгруппируй (выпиши)

только однозначные (02468)

двузначные (10 12 14 16 18 20)

Можно ли продолжить ряды?

— /первый — нет, т.к. однозначные числа от 0 до 9/

РАБОТА НАД ТЕМОЙ УРОКА. Вот и назван маршрут

И друзья всех нас ждут

Как приятно будет им

Услышать имена свои

Так какие геометрические фигуры вы знаете? Назовите их.

Назовите только те фигуры, которые сейчас перед вами.

/ на партах у детей наборы геометрических фигур/

У вас есть минута одну из фигур с помощью карандаша и линейки начертить в тетради.

И две минуты на то, чтобы превратить эту фигуру, в какой- нибудь предмет. Делаем очередную запись в нашем дневнике.

/ дети рисуют и дополняют фигуру/

Я думаю, что жителям страны Геометрии такие превращения понравятся. А вы как считаете?

№ 4. Квадрат и треугольник. Их свойства.

Пока вы рисовали, в стране Геометрии произошёл странный случай. Вот послушайте, что мне удалось услышать и увидеть.

Жили-были два брата: Треугольник и Квадрат.

— Почему ты злишься, брат?

Тот кричит ему в ответ: смотри, ты полней меня и шире. У меня углов лишь три, у тебя же их — четыре.

Но квадрат ответил: брат, я же старше. Я — квадрат! И сказал ещё нежней: неизвестно, кто нужней!

Но настала ночь и к брату, натыкаясь на столы, младший лезет воровато срезать старшему углы, (срезаем углы у квадрата) Уходя, сказал:

— Приятных я тебе желаю снов! Спать ложился — был Квадратом, а проснёшься без углов.

Но на утро младший брат страшной мести был не рад.

Какая фигура получилась? (восьмиугольник).

Расскажите всё, что знаете о квадрате.

Можно ли начертить в тетради квадрат, зная длину одной стороны?

Записать примеры в столбик, решить их.

Сравните периметр 1 варианта с периметром 2 варианта.

№ 5. Практическая работа. Изготовление лодочки.

Пусть та лодочка, которую мы сейчас сделаем, станет для каждого из вас символом новых открытий.

/изготовление лодочки из квадрата/.

Приложи линейку к линии диагонали и проведи ещё одну линию.

Поменяйся с одноклассниками треугольниками

Что интересного было для вас на уроке?

Что вы знаете про геометрические фигуры и их свойства?

Для современного этапа развития школьного математического образования характерен переход от экстенсивного обучения к интенсивному. Вновь актуальными становятся проблемы развития интуиции, образного мышления, а также способности мыслить творчески, не стандартно. Для формирования высокой мотивации учебного процесса, а также в развитии всех форм мышления младшего школьника, ведущую роль важно отводить геометрии.

Геометрический материал в программе начальной школы не выделяется в самостоятельный раздел, он включается в программу каждого года обучения. Надо отметить его тесную связь с другими разделами математики, и прежде всего с арифметикой. В основе этой связи лежит возможность установления отношений между числом и геометрической фигурой, что позволяет использовать фигуры при формировании понятий числа, свойств чисел и операций над ними.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Скоростное чтение

Курс повышения квалификации

Специфика преподавания предмета «Родной (русский) язык» с учетом реализации ФГОС НОО

Ищем педагогов в команду «Инфоурок»

Для современного этапа развития школьного математического образования характерен переход от экстенсивного обучения к интенсивному. Вновь актуальными становятся проблемы развития интуиции, образного мышления, а также способности мыслить творчески, не стандартно. Для формирования высокой мотивации учебного процесса, а также в развитии всех форм мышления младшего школьника, ведущую роль важно отводить геометрии.

Геометрический материал в программе начальной школы не выделяется в самостоятельный раздел, он включается в программу каждого года обучения. Надо отметить его тесную связь с другими разделами математики, и прежде всего с арифметикой. В основе этой связи лежит возможность установления отношений между числом и геометрической фигурой, что позволяет использовать фигуры при формировании понятий числа, свойств чисел и операций над ними.

Номер материала: 176537

Не нашли то что искали?

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Комиссия РАН призвала отозвать проект новых правил русского языка

Время чтения: 2 минуты

В России стартовал прием заявок на конкурс для журналистов-школьников «Медиабум»

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Российские школьники установили рекорд на олимпиаде по астрономии

Время чтения: 2 минуты

Отказавшихся от вакцинации сотрудников МГУ отстранили от работы со студентами

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник