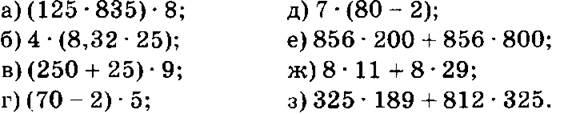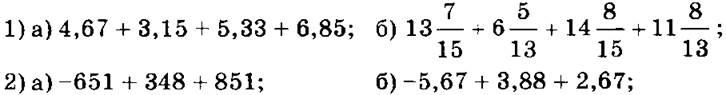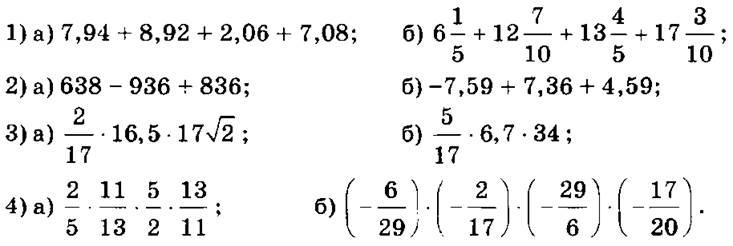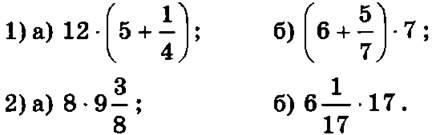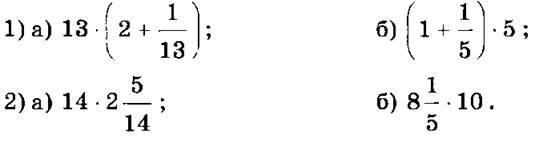что такое свойство действий над числами в алгебре
Свойства действий над числами
Напомним основные свойства сложения и умножения чисел.
1) Переместительное свойство: для любых чисел а и b верны равенства
2) Сочетательное свойство: для любых чисел a, b и с верны равенства
(а + b) + с = а + (b + с), (ab)c = a(bc).
3) Распределительное свойство:
Из переместительного и сочетательного свойств сложения следует:
в любой сумме можно как угодно переставлять слагаемые и произвольным образом объединять их в группы.
П р и м е р 1. Вычислим сумму 1,23 + 13,5 + 4,27.
Для этого удобно объединить первое слагаемое с третьим. Получим
1,23 + 13,5+ 4,27 = (1,23+ 4,27)+ 13,5 = 5,5 + 13,5= 19. 
Из переместительного и сочетательного свойств умножения следует:
в любом произведении можно как угодно переставлять множители и произвольным образом объединять их в группы.
П р и м е р 2. Найдём значение произведения 1,8 • 0,25 • 64 • 0,5.
Объединив первый множитель с четвёртым, а второй — с третьим, получим
1,8 • 0,25 • 64 • 0,5 = (1,8 • 0,5) • (0,25 • 64) = 0,9 • 16= 14,4.
Распределительное свойство справедливо и в том случае, когда число умножается на сумму трёх и более слагаемых.
Например, для любых чисел а, b, с и d верно равенство
а (b + с + d) = ab + ас + ad.
Мы внаем, что вычитание можно заменить сложением, прибавив к уменьшаемому число, противоположное вычитаемому:
Пример 3. Найдём значение выражения 3,27- 6,5-2,5+ 1,73.
Применив свойства сложения, получим
Пример 4. Вычислим произведение 
Множитель 
можно рассматривать как сумму чисел 
и 
Используя распределительное свойство умножения, получим
Сочетай, перемещай, свойства действий
Как найти значение выражения используя свойства арифметических действий?
Напомним известные уже из арифметики главнейшие свойства действий сложения, вычитания, умножения и деления, так
как этими свойствами придется часто пользоваться и в алгебре.
Свойства сложения
Переместительный закон сложения
Пример:
3 + 8 = 8 + 3; 5 + 2 + 4 = 2 + 5 + 4 = 4 + 2 + 5.
В общем случае:
a+b+c=c+a+b
Стоит иметь ввиду, что число слагаемых может быть и более трёх.
Сочетательный закон сложения
Пример:
3 + 5 + 7 = 3 + (5 + 7) = 3 + 12 = 15;
4 + 7+11+6 + 5 = 7 +(4+ 5)+ (11+6) = 7 + 9+17 = 33.
В общем случае:
а + b + с = а+(b + с) = b+(а + с) и т. п.
Иногда этот закон выражают так: слагаемые можно соединять в какие угодно группы.
Чтобы прибавить к какому-либо числу сумму нескольких чисел, можно прибавить отдельно каждое слагаемое одно за другим.
Пример:
5 + (7 + 3) = (5 + 7) + 3 = 12 + 3 = 15.
В общем случае:
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть из какого-нибудь числа сумму нескольких чисел, можно вычесть отдельно каждое слагаемое одно за другим.
Например:
20 — (5+ 8) = (20 — 5) — 8 = 15 — 8 = 7.
В общем случае:
а — (b + с + d+ …) = а — Ь — с — d — …
Свойство сложения разности чисел
Чтобы прибавить разность двух чисел, можно прибавить уменьшаемое и затем вычесть вычитаемое.
Свойство вычитания разности из числа
Чтобы вычесть разность, можно сначала прибавить вычитаемое и затем вычесть уменьшаемое.
Например:
18-(9-5) = 18 + 5-9= 14.
Вообще:
а — (Ь — с) = а + с — b.
Свойства умножения
Переместительный закон умножения
Сочетательный закон умножения
Так:
7*3*5 = 5*(3*7) = 5*21 = 105.
Вообще:
abc = а(bс) = b(ас) и т. п.
Умножение числа на произведение чисел
Чтобы умножить какое-либо число на произведение нескольких сомножителей, можно умножить это число на
первый сомножитель, полученный результат умножить на второй сомножитель и т. д.
Так:
3*(5*4) = (3*5)*4= 15*4 = 60.
Вообще:
a•(bcd…) = <[(a·b)•c]•d>…
Чтобы умножить произведение нескольких сомножителей на какое-либо число, можно умножить на это число один
из сомножителей, оставив другие без изменения.
Так:
3 • 2 • 5 • 3 = (3 • 3) • 2 • 5 = 3 • (2 • 3) • 5 = 3 • 2 • (5 • 3).
Вообще:
(abc.. )m = (аm)bс… = а(bm)с… и т. п.
Умножение числа на сумму чисел
Чтобы умножить сумму на какое-либо число, можно каждое слагаемое умножить на это число и полученные ре-
результаты сложить.
В силу переместительного закона умножения это же свойство можно выразить так: чтобы умножить какое-либо число на
сумму нескольких чисел, можно умножить это число на каждое слагаемое отдельно и полученные результаты сложить.
Так:
5·(4 + 6) = 5·4 + 5·6.
Вообще:
r·(а + Ь + с +…) = rа + rb + rс + …
Это свойство называется распределительным законом умножения, так как умножение, производимое над суммой, распределяется на каждое слагаемое в отдельности.
Распределительный закон умножения для разности чисел
Распределительный закон можно применять и к разности.
Так:
(8 — 5) • 4 = 8 • 4 — 5 • 4;
7 • (9 — 6) = 7 • 9 — 7 • 6.
Вообще:
(а — b)с = ас — bc,
а(b — с) = ab — ас,
т. е. чтобы умножить разность на какое-либо число, можно умножить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй; чтобы умножить какое-либо число на разность, можно это число умножить
отдельно на уменьшаемое и вычитаемое и из первого результата вычесть второй.
Свойства деления
Деление суммы на число
Чтобы разделить сумму на какое-либо число, можно разделить на это число каждое слагаемое отдельно и полученные результаты сложить:
Деление разности на число
Чтобы разделить разность на какое-либо число, можно разделить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй:
Деление произведения на число
Чтобы разделить произведение нескольких сомножителей на какое-либо число, можно разделить на это число один
из сомножителей, оставив другие без изменения:
(40 • 12 • 8) : 4 = (40:4) • 12 • 8 = 10 • 12 • 8 = 40 • 12 • 2.
Вообще:
(a·b·c…) : t = (а : t)bс… = а(b : t)с… и т. д.
Деление числа на произведение
Чтобы разделить какое-либо число на произведение нескольких сомножителей, можно разделить это число на
первый сомножитель, полученный результат разделить на второй сомножитель и т.д.:
120 : (12 • 5 • 3) = [(120 : 2) : 5] : 3 = (60 : 5) : 3 = 12 : 3 = 4.
а : (bcd …) = [(а : b) : с] : d… и т. п.
Укажем еще следующее свойство деления:
Если делимое и делитель умножим (или разделим) на одно и то же число, то частное не изменится.
Поясним это свойство на следующих двух примерах:
1)8:3 = 8/3|,
умножим делимое и делитель, положим, на 5; тогда получим
новое частное: (8*5)/(3*5)
которое по сокращении дроби на 5 даст прежнее частное — 8/3
Вообще, какие бы числа a, b и m ни были, всегда
(am) : (bm) = а : b, что можно написать и так:
am/bm= a/b
Свойства действий над числами
Сложение
Сложение многозначных чисел производится поразрядно.
Законы сложения.
Пример. 310 + 1454 = 1454 + 310. Каким бы мы способом не складывали результат будет равен 1764.
Пример: (329 + 85) + 120 = 329 + (85 + 120) = 329 + 205 =534;
Вычитание
Свойства действий вычитания:
Задача как пример действий сложения и вычитания
Вычислите удобным способом:
Применяем 2-й и 5-й законы вычитания:
Умножение
Умножить число а на число b (b>1)- значит найти сумму b слагаемых (каждое слагаемое равно а).
Если b = 1, то а x 1 = a.
a (первый множитель) x b (второй множитель) = c (произведение)
Например: 57 + 57 + 57 + 34 + 34 = 57 х 3 + 34 х 2 = 171 + 68 + 239
Законы умножения
Пример. 15 х 110 = 110 х 15.
Пример: (9 х 30) х 10= 9 х (30 х 10) = 9 х 300= 2700;
(65 х 25) х 44 = (25 х 65) х 44 = 25 х (65 X 44)=25 х 2860 = 71500.
a x (b + c) = a x b + a x c;
Задачи как пример действия умножения
Задача 1. Вычислить удобным способом:
1) (37 х 125) х 8 = 37 х (125 х 8) = 37 х 1000 = 37000;
Задача 2. 1 квт/ч стоит 12 руб. Электрический утюг за 1 ч работы расходует 2 квт/ч. Утюгом два дня гладили бельё: в первый день- 3 ч, во второй- 2ч. Сколько стоит электроэнергия, израсходованная за два дня? Задачу решите сами, а мы дадим только ответы: за 3 ч- 72руб; за 2ч- 48руб.
Деление
а (делимое) : b (делитель) = с (частное)
Законы деления:
2224222 : 2222 = 1001
Закон деления суммы (разности) на число:
Пример: (4800 + 9300) : 300 = 4800 : 300 + 9300 : 300 = 16 + 31 + 47.
Закон деления произведения на число:
(а х b) :с = (а : с) х b = (b : с) х а, с не равно 0.
Пример: (125 х 27) : 25 = (125 : 25) х 27 = 5 х 27 = 135.
Свойства действий над числами
Переместительное и сочетательное свойство гласит, что в любой сумме можно как угодно переставлять слагаемые и произвольно объединять их в группы (от перемены мест слагаемых сумма не меняется!).
Распределительное свойство справедливо тогда, когда число умножается на сумму трех и более слагаемых.
Свойства действий над числами
70. а) переместительное свойство; б) переместительно свойство; в) сочетательное свойство; г) распределительное свойство.
71. а) 3,17 + 10,2 + 0,83 + 9,8 = (3,17 + 0,83) + (10,2 + 9,8) = 4 + 20 = 24;
б) 4,11 + 15,5 + 0,89 + 4,4 = (4,11 + 0,89) + (15,5 + 4,4) = 5 + 19,9 = 24,9;
72. а) 8,91 + 25,7 + 1,09 = (8,91 + 1,09) + 25,7 = 10 + 25,7 = 35,7;
б) 6,64 + 7,12 + 2,88 = 6,64 + (7,12 + 2,88) = 6,64 + 10 = 16,64;
73. a) 
Использовали: 1) переместительное свойство; 2) сочетательное свойство,
Использовали: 1) переместительное свойство; 2) сочетательное свойство.
75. а) 50 • 1,34 • 0,2 = (50 • 0,2) • 1,34 = 10 • 1,34 = 13,4;
г) 0,47 • (0,4 • 25) = 0,47 • 10 = 4,7.
77. а) 3,5 • 6,8 + 3,5 • 3,2 = 3,5 • (6,8 + 3,2) = 3,5 • 10 = 35;
78. а) 15,7 • 3,09 + 15,7 • 2,91 = 15,7 • (3,09 + 2,91) = 15,7 • 6 = 94,2;
79. а) 24 • 17 + 17 • 6 = 17 • (24 + 6) = 17 • 30. 30 делиться на 5 значит и 24 • 17 + 17 • 6 делиться на 5.
80. 5 • а — стоимость 5 наборов карандашей; 10 х b — стоимость 10 альбомов; 5 • а + 10 • 6 — стоимость покупки.
81. υср — средняя скорость движения автомобиля.
Урок по теме «Свойства действий над числами. Решение задач»
Урок математики по теме «Свойства действий над числами. Решение задач»
Просмотр содержимого документа
«Урок по теме «Свойства действий над числами. Решение задач»»
ТЕМА: Свойства действий над числами. Решение задач.
ЦЕЛЬ УРОКА: Формирование у учащихся умений применять свойства действий над числами для рациональных вычислений.
Нацелить учащихся на урок
Проверка домашнего задания
Актуализация опорных знаний
Формирование умений применять свойства действий над числами для рационализации вычислений
Упражнения на повторение
Повторить нахождение координаты точки на числовой прямой
Подведение итогов урока
Обобщить теоретические сведения, полученные на уроке
Сообщение домашнего задания
Разъяснить содержание домашнего задания
I. Организационный момент.
II. Проверка домашнего задания.
III. Актуализация опорных знаний.
1. Сформулировать переместительное и сочетательное свойства сложения и умножения; распределительное свойство.
2. Вычислить наиболее удобным способом:
Прокомментировать, какие свойства действий над числами определяют способы решения.
3. Как трехзначное число умножить на 1001?
4. Вынести общий множитель за скобки:
IV. Самостоятельная работа (с последующей проверкой).
Вариант I Вариант II
1. Вычислить наиболее рациональным способом:
2. Найдите значение выражения, используя распределительное свойство умножения:
V. Упражнения на повторение.
№№ 79, 83, 84 — коллективно, с записью на доске.