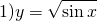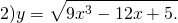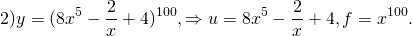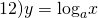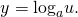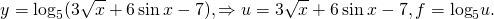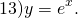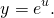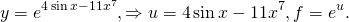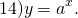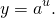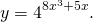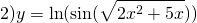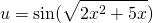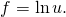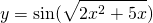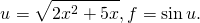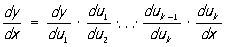что такое сложная функция

Сложная функция. Производная сложной функции

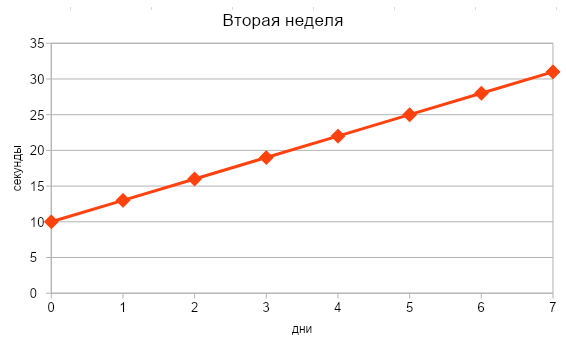
Раз ты зашел сюда, то уже, наверное, успел увидеть в учебнике эту формулу

и сделать вот такое лицо:

Друг, не переживай! На самом деле все просто до безобразия. Ты обязательно все поймешь. Только одна просьба – прочитай статью не торопясь, старайся понять каждый шаг. Я писал максимально просто и наглядно, но вникнуть в идею всё равно надо. И обязательно реши задания из статьи.

Что такое сложная функция?

Представь, что ты переезжаешь в другую квартиру и поэтому собираешь вещи в большие коробки. Пусть надо собрать какие-нибудь мелкие предметы, например, школьные письменные принадлежности. Если просто скидать их в огромную коробку, то они затеряются среди других вещей. Чтобы этого избежать, ты сначала кладешь их, например, в пакет, который затем укладываешь в большую коробку, после чего ее запечатываешь. Этот «сложнейший» процесс представлен на схеме ниже:

Например, возьмем x и «запакуем» его в функцию косинуса :

Что получится в итоге? Да, верно, будет «пакет с вещами в коробке», то есть «косинус икса в кубе».

В школьном курсе видов этих самых «упаковок» совсем мало, всего четыре :

Напиши теперь сам функции, где икс:
— сначала «упаковывается» в косинус, а потом в показательную функцию с основанием \(3\);
— сначала в пятую степень, а затем в тангенс;
— сначала в логарифм по основанию \(4\) , затем в степень \(-2\).

Ответы на это задание посмотри в конце статьи.

А можем ли мы «упаковать» икс не два, а три раза? Да, без проблем! И четыре, и пять, и двадцать пять раз. Вот, например, функция, в которой икс «упакован» \(4\) раза:

«Распаковка» сложной функции

Теперь правильный ответ: сначала икс «упаковали» в \(4\)-ую степень, потом результат упаковали в синус, его в свою очередь поместили в логарифм по основанию \(2\), и в конце концов всю эту конструкцию засунули в степень пятерки.

То есть разматывать последовательность надо В ОБРАТНОМ ПОРЯДКЕ. И тут подсказка как это делать проще: сразу смотри на икс – от него и надо плясать. Давай разберем несколько примеров.

\(x → \log_2⁡x → tg⁡(\log_2⁡x )\)

Еще пример: \(y=\cos⁡<(x^3 )>\). Анализируем – сначала икс возвели в куб, а потом от результата взяли косинус. Значит, последовательность будет: \(x → x^3 → \cos⁡<(x^3 )>\). Обрати внимание, функция вроде бы похожа на самую первую (там, где с картинками). Но это совсем другая функция: здесь в кубе икс (то есть \(\cos⁡<(x·x·x)>)\), а там в кубе косинус \(x\) (то есть, \(\cos⁡x·\cos⁡x·\cos⁡x\)). Эта разница возникает из-за разных последовательностей «упаковки».

Последний пример (с важной информацией в нем): \(y=\sin⁡<(2x+5)>\). Понятно, что здесь сначала сделали арифметические действия с иксом, потом от результата взяли синус: \(x → 2x+5 → \sin⁡<(2x+5)>\). И это важный момент: несмотря на то, что арифметические действия функциями сами по себе не являются, здесь они тоже выступают как способ «упаковки». Давай немного углубимся в эту тонкость.

Однако если к такой комбинации применить еще одну функцию – будет уже сложная функция, так как «упаковок» станет две. Смотри схему:

Хорошо, давай теперь сам. Напиши последовательность «заворачивания» функций:
\(y=cos<⁡(sin⁡x)>\)
\(y=5^\)
\(y=arctg⁡<11^x>\)
\(y=log_2⁡(1+x)\)
Ответы опять в конце статьи.

Внутренняя и внешняя функции

Зачем же нам нужно разбираться во вложенности функций? Что нам это дает? Дело в том, что без такого анализа мы не сможем надежно находить производные разобранных выше функций.

Вот в этом примере: \(y=tg⁡(log_2⁡x )\), функция \(\log_2⁡x\) – внутренняя, а — внешняя.

Заполни пропуски в таблице:

Производная сложной функции

Браво нам, мы всё ж таки добрались до «босса» этой темы – собственно, производной сложной функции, а конкретно, до той самой ужасной формулы из начала статьи.☺

Формула эта читается так:

Производная сложной функции равна произведению производной внешней функции по неизменной внутренней на производную внутренней функции.

И сразу смотри схему разбора «по словам» чтобы понимать, что к чему относится:

Ответ: это обычная производная внешней функции, при которой изменяется только внешняя функция, а внутренняя остается такой же. Все равно непонятно? Хорошо, давай на примере.

Пусть у нас есть функция \(y=\sin⁡(x^3 )\). Понятно, что внутренняя функция здесь \(x^3\), а внешняя . Найдем теперь производную внешней по неизменной внутренней.

Тогда производная внешней функции по неизменной внутренней для нашего случая будет \(\cos⁡(x^3)\). То есть, мы взяли ее как обычную производную синуса, а содержимое синуса (внутреннюю функцию) просто скопировали в полученную производную (косинус), ничего в ней не меняя.

Таким образом, на данный момент имеем:

Осталась «производная внутренней функции». Ну, это совсем легко – обычная производная от внутренней функции, при этом внешняя не влияет вообще никак. В нашем примере, производная от \(x^3\).

Все, теперь можем писать ответ:

Вот так. Давай еще один пример разберем.

Пусть надо найти производную функции \(y=(\sin⁡x )^3\).

Анализируем. Последовательность «заворачивания» у нас такая: \(x → \sin⁡x → (\sin⁡x )^3\). Значит, в данном примере внутренняя функция это \(\sin⁡x\), а внешняя .

Производная внешней по внутренней – это производная куба (содержимое куба при этом не меняется). Так как , а в нашем случае в куб «завернут» \(\sin⁡x\), то производная внешней будет \(3(\sin⁡x)^2\). То есть, имеем:

Ну, а производная внутренней – это просто производная синуса икс, то есть косинус икс.

Понятно?
Ладно, ладно, вот еще один пример с разбором. ☺

Пример. Найти производную сложной функции \(y=\ln(x^2-x)\).

Ну и напоследок можно немного «причесать» ответ, чтоб никто не докопался:

Что, еще примеров желаешь? Легко.

Еще пример с важным замечанием в нем.

Пример. Найти производную сложной функции \(y=\sqrt \)
Вложенность функций: \(x → x^6 → \sqrt\)
Внутренняя: \(x^6\) Внешняя:
Производная внешней по внутренней: \(\sqrt‘=\) \(\frac<1><2\sqrt>\)
Производная внутренней: \((x^6)’= 6x^5\)
Имеем: \((\sqrt)’=\) \(\frac<1><2\sqrt>\) \(·6x^5\)
И теперь упростим ответ. Вспомним свойство корня: \(\sqrt[b] =x^<\frac>\). Тогда \(\sqrt=x^<\frac<6><2>>=x^3\). С учетом этого получаем:

Всё. А теперь, собственно, важное замечание:

Давай рассмотрим пример, где эта идея нам сильно поможет.

Пример. Найти производную сложной функции \(y=\ln⁡(x^3)\).
Можно, конечно, рассмотреть вложенность функций: \(x → x^3 → \ln⁡(x^3 )\), разобрать на внутреннюю и внешнюю и так далее. Но можно вспомнить свойство логарифма: \(\log_a⁡=c·\log_a<⁡b>\). И тогда функция получается \(y=\ln⁡(x^3 )=3\ln⁡x\). Отлично! Берем производную:

Теперь задачка посложнее, для продвинутых. Решим пример с тройной вложенностью!

Пример. Найти производную сложной функции \(y=3^<\sin⁡(x^4+1)>\).
Вложенность функций: \(x → x^4+1 → \sin⁡(x^4+1) → 3^<\sin⁡(x^4+1)>\)
Внутренняя: \(x^4+1\) Средняя: Внешняя:
Сначала производная внешней по средней. Вспоминаем таблицу производных: . Значит, в нашем случае будет \(3^<\sin⁡(x^4+1)>·\ln⁡3\).
Хорошо, теперь производная средней по внутренней. По таблице: . Значит, мы получим, \(\sin⁡(x^4+1)’=\cos⁡(x^4+1)\).
И наконец, производная внутренней: \((x^4+1)’=(x^4 )’+(1)’=4x^3\).
Отлично. Теперь собираем все вместе, перемножая отдельные производные:

Готово. Да, это ответ. ☺

Ну, а что ты хотел, я сразу сказал – пример для продвинутых! А представь, что будет с четырехкратной или пятикратной вложенностью? ☺

Пример: Найти производную сложной функции \(y=tg⁡(7^x)\).

Ну, теперь думаю всё понятно? И снова повторю – не пугайся сложных конструкций в ответах и промежуточных вычислениях. Они «на лицо ужасные», но зато добрые (в смысле простые) внутри. ☺ Пойми принцип и делай все последовательно.

Последний пример. Такие задания в разных вариациях весьма часто дают на контрольных и тестах. Он вроде как считается сложным. ☺ Хех, наивные учителя. ☺

Пример: Найти производную сложной функции \(y=\sqrt[3]<(x^5+2x-5)^2>\).

Казалось бы, опять у нас тройная вложенность функций:

Но давай снова воспользуемся свойством корня \(\sqrt[b] =x^<\frac>\) и преобразуем нашу функцию к виду:

Вот так. И теперь у нас вложенность двойная: \(x → x^5+2x-5 → (x^5+2x-5)^<\frac<2><3>>\)
При этом функция осталась той же! Удобное свойство, однако. Стоит его запомнить, да? ☺ Ладно, поехали дальше.
Внутренняя функция: \(x^5+2x-5\). Внешняя: .
Производная внешней по внутренней. По таблице производных общая формула производной степенной функции: . Получаем: . Тогда в нашем случае будет: \(\frac<2><3>(x^5+2x-5)^<-\frac<1><3>>\).
Производная внутренней: \((x^5+2x-5)’=5x^4+2\).
Общий результат: \(y ‘=(\sqrt[3]<(x^5+2x-5)^2>)’=((x^5+2x-5)^<\frac<2><3>> )’=\frac<2><3>(x^5+2x-5)^<-\frac<1><3>>·(5x^4+2)\).

Ну, и перемножаем дроби.

Найти производные функций:

Ответы ко всем заданиям (вперемежку).

\(x → 1+x → \log_2⁡ <(1+x)>\)
\(x → 11^x → arctg⁡(11^x) \)
\(x → x^7 → 5^\)
\(x → \sin⁡x → \cos⁡(\sin⁡x)\)

Источник

Примеры сложных функций

Сложная функция — это функция от функции. Если u — функция от x, то есть u=u(x), а f — функция от u: f=f(u), то функция y=f(u) — сложная.

А u в этом случае называют промежуточным аргументом. Еще часто f называют внешней функцией, а u — внутренней. Лучший способ понять, что такое сложная функция — рассмотреть примеры сложных функций.

1) y=sin x — эта функция «простая». Синус зависит от x. Как только вместо x под знаком синуса появится выражение, зависящее от x, даже самое простое — такая функция называется сложной. То есть y=sin u — сложная функция, если u — некоторая функция от x. Примеры сложных функций с синусом:

y=sin (x+1). Эта функция — сложная. Внутренняя функция u здесь равна x+1, а внешняя функция f — это синус. То есть u=x+1, f=sin u.

y=sin (5x-2x³+3). Внутренняя функция u=5x-2x³+3, внешняя функция f=sin u.

y=sin (x/7). Внутренняя функция u=x/7, внешняя функция f=sin u.

2) y=cos x — «простая» функция. y=cos u — сложная функция, если u — некоторая функция, зависящая от x. Примеры сложных функций с внешней функцией — косинусом:

y=cos (4-11x). Внутренняя функция u=4-11x, внешняя функция — косинус: y=cos u.

3) y=tg x — «простая» функция. y = tg u — сложная функция, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — тангенс:

y=tg(17+5x²). Внутренняя функция u=17+5x², внешняя — y=tg u.

y=tg(9-x). Внутренняя u=9-x, внешняя — y=tg u.

4) y=ctg x — «простая» функция. y=ctg u — сложная функция, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — котангенс:

y=ctg(2x+6). Внутренняя функция u=2x+6, внешняя — y=ctg u.

5) y=√x — «простая» функция. y=√u — сложная, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — квадратный корень:

Здесь внутренняя функция y=sin x, а внешняя — f=√u.

6) y=xⁿ — «простая» функция. y=uⁿ — сложная, если u=u(x). Примеры сложных функция для случая, когда внешняя функция — степенная.

y=sin³x. Внутренняя функция y=sin x (так как sin³x=(sin x)³), внешняя — у=u³.

7) y=arcsin x — «простая» функция. y=arcsin u — сложная, когда u=u(x).

Например, y=arcsin (3x-9) — сложная функция. Внутренняя функция u=3x-9, внешняя — f=arcsin u.

y=arcsin (17-5x³). u=17-5x³, f=arcsin u.

8) y=arccos x — «простая» функция. y=arccos u — сложная, при u=u(x).

Например, y=arccos (34x+5) — сложная функция. Внутренняя функция u=34x+5, внешняя — f=arccos u.

9) y=arctg x — «простая» функция. y=arctg u — сложная, при u=u(x).

Например, y= arctg (6x+2x³-7). Внутренняя функция u =6x+2x³-7, внешняя — f=arctg u.

10) y=arcctg x — «простая функция. При u=u(x) функция y=arcctg u — сложная.

Например, y= arcctg(2-11x+x²) — сложная функция. u=2-11x+x², f= arcctg u.

11) y=ln x — «простая» функция. y= ln u — сложная, при u=u(x).

Например, y=ln(4+32x-2x³). Внутренняя функция y=4+32x-2x³, внешняя — f=ln u.

Это — «простая» функция. А вот при u=u(x) получаем логарифм сложной функции:

Эта функция — «простая» (называется экспонента). А вот если в показателе стоит не x, а некоторая функция от икса: u=u(x), то это — уже экспонента сложной функции:

Эта функция — «простая». А вот если в показателе стоит не x, а некоторое выражение с x — функция u=u(x), то это уже степень сложной функции:

Эта функция — сложная. Внутренняя функция u=8x³+5x, а внешняя — степень сложной функции

Следует добавить, что внутренняя функция u, в свою очередь, может быть сложной функцией. И таких «вложенных» функций может быть несколько (теоретически — сколько угодно).

1) y=cos³(3x-12). Здесь внутренняя функция u =cos(3x-12), а внешняя функция f=u³. Но внутренняя функция y=cos(3x-12), в свою очередь, тоже является сложной функцией. Для нее внутренняя функция u=3x-12, а внешняя f=cos x.

Сначала рассмотрим эту функцию, как логарифм сложной функции. Тогда внутренняя функция

В свою очередь, функция

— тоже сложная. Это — синус сложной функции, то есть

Но u — снова сложная функция. Здесь уже внутренняя функция u=2x²+5x, а внешняя f=√u.

Источник

Таблица производных функций

10 класс, 11 класс, ЕГЭ/ОГЭ

Что такое производная и зачем она нужна

Прежде чем переходить к таблице для вычисления производных, дадим определение производной. В учебнике оно звучит так:

Производная функции — это предел отношения приращения функции к приращению ее аргумента, при условии, что приращение аргумента стремится к нулю.

Если же говорить простыми словами, то производная функции описывает, как и с какой скоростью эта функция меняется в данной конкретной точке. Процесс нахождения производной называется дифференцированием.

Объясним на примере: допустим, Маша решила по утрам делать зарядку и стоять в планке. В первую неделю она держалась каждый день по 10 секунд, но начиная со второй недели смогла стоять в планке с каждым днем на 3 секунды дольше. Успехи Маши можно описать следующими графиками:

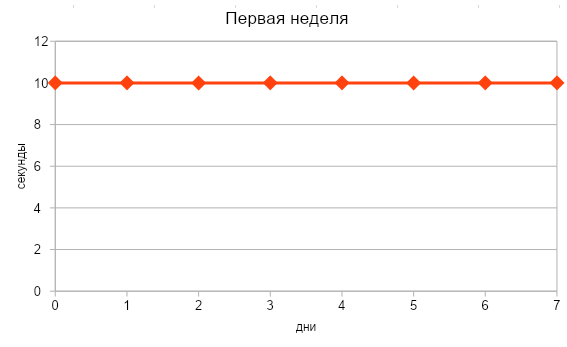
Очевидно, что в первую неделю результаты Маши не менялись (т. е. были константой), скорость прироста оставалась нулевой. Если мы заглянем в таблицу производных простых функций, то увидим, что производная константы равна нулю.

Во вторую неделю время выполнения планки с 10 сек начало увеличиваться на 3 сек ежедневно.

Снова смотрим в таблицу дифференцирования производных, где указано, что производная от х равна 1.

Вот так с помощью таблицы производных и элементарной математики мы докажем, что успехи Маши росли со скоростью 3 сек в день.

Это был очень простой пример, который в общих чертах объясняет азы дифференциального исчисления и помогает понять, для чего нужны формулы из таблицы производных функций. Но разобраться в решении задач, где скорость меняется нелинейно, конечно, не так просто.

Быстрее освоить производные поможет обучение на курсах по математике в онлайн-школе Skysmart.

Производные основных элементарных функций

Таблица производных для 10 и 11 класса может включать только элементарные часто встречающиеся функции. Приведем несколько формул, которых достаточно для решения большинства задач.

Источник

Сложная функция

Смотреть что такое «Сложная функция» в других словарях:

сложная функция — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN composite function … Справочник технического переводчика

сложная функция — функция от функции. Если величина у является функцией от u, то есть у = f(u), а u, в свою очередь, функцией от х, то есть и = φ(х), то у=F(х) является сложной функцией от х, то есть y=F(x)=f[φ(x)]. * * * СЛОЖНАЯ ФУНКЦИЯ СЛОЖНАЯ ФУНКЦИЯ, функция… … Энциклопедический словарь

СЛОЖНАЯ ФУНКЦИЯ — функция, представленная как композиция нескольких функций. Если множество значений Yi функции fi содержится во множестве определения Х i+1 функции fi+1, т. е. то функция определяемая равенством наз. сложной функцией или (п 1) кратной композицией… … Математическая энциклопедия

СЛОЖНАЯ ФУНКЦИЯ — функция от функции. Если величина у является функцией от и, то есть у = f(u), а и, в свою очередь, функцией от х, то есть u = ф(х), то y = F(x) является С. ф. от х, то есть y = F(x) = f[ф(x)] … Естествознание. Энциклопедический словарь

Сложная функция — … Википедия

Сложная трёхчастная форма — Сложная трёхчастная форма музыкальная репризная трёхчастная форма, первая часть которой сложнее периода. Чаще всего первая часть представляет собой простую двух или трёхчастную форму, но иногда бывает и сложнее (кроме того, средний раздел… … Википедия

МОДУЛЯРНАЯ ФУНКЦИЯ — эллиптическая модулярная функция, одного комплексного переменного автоморфная функция комплексного переменного ассоциированная с группой Г всех дробно линейных преобразований вида где целые действительные числа (эта группа наз. модулярной).… … Математическая энциклопедия

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия

АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ — 1) А. н. интеграла свойство неопределенного интеграла (Лебега). Пусть функция f интегрируема на множестве Е. Интеграл от f на измеримых подмножествах является абсолютно непрерывной функцией (см. ниже п. 3) множества относительно меры m, т. е. для … Математическая энциклопедия

Источник

Сложные и обратные функции

Содержимое разработки

Тема : Сложная и обратная функции

Сложная функция — это функция от функции. Если u — функция от x, то есть u=u(x), а f — функция от u: f=f(u), то функция y=f(u) — сложная.

А u в этом случае называют промежуточным аргументом. Еще часто f называют внешней функцией, а u — внутренней. Лучший способ понять, что такое сложная функция — рассмотреть примеры сложных функций.

1) y=sin x — эта функция «простая». Синус зависит от x. Как только вместо x под знаком синуса появится выражение, зависящее от x, даже самое простое — такая функция называется сложной. То есть y=sin u — сложная функция, если u — некоторая функция от x. Примеры сложных функций с синусом:

y=sin (x+1). Эта функция — сложная. Внутренняя функция u здесь равна x+1, а внешняя функция f — это синус. То есть u=x+1, f=sin u.

Что такое обратная функция? Как найти функцию, обратную данной?

Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.

Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.

Чтобы найти функцию, обратную данной функции y=f(x), надо:

1) В формулу функции вместо y подставить x, вместо x — y:

2) Из полученного равенства выразить y через x:

Найти функцию, обратную функции y=2x-6.

Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.

Источник