что такое симметричное множество

Бинарные операции над упорядоченными множествами

В предыдущей статье я писал о бинарных операциях над неупорядоченными множествами. В этой статье мы рассмотрим алгоритмы с меньшей сложностью выполнения, для упорядоченных множеств.

I. Пересечение упорядоченных множеств

Пересечение двух упорядоченных множеств A и B — это множество только с теми элементами A и B, которые одновременно принадлежат обоим множествам, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных множеств A и B соответственно.

Сделал небольшую анимацию, чтобы показать как работает алгоритм.

Пример реализации на javascript:

Обращение к функции:

II. Разность упорядоченных множеств

Разность двух упорядоченных множеств A и B — это множество с элементами A, не совпадающими с элементами B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.

III. Объединение упорядоченных множеств

Объединение двух упорядоченных множеств A и B — это множество с элементами A и элементы множества B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.

IV. Симметрическая разность упорядоченных множеств

Симметрическая разность двух упорядоченных множеств A и B — это такое множество, куда входят все те элементы первого упорядоченного множества, которые не входят во второе упорядоченное множество, а также те элементы второго упорядоченного множества, которые не входят в первое упорядоченное множество. Сложность алгоритма O(2(m+n)), где m и n — длины входных упорядоченных множеств A и B соответственно.

По сути это вычитание множеств, сначала A из B, затем B из A.

Источник

Разработка урока «Четные и нечетные функции»

разработка урока по теме Четные и нечетные функции

Содержимое разработки

ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ

сформировать понятие чётности и нечётности функции, учить умению определять и использовать эти свойства при исследовании функций, построении графиков;

развивать творческую активность учащихся, логическое мышление, умение сравнивать, обобщать;

воспитывать трудолюбие, математическую культуру; развивать коммуникативные качества.

Формы работы: фронтальная и групповая с элементами поисково-исследовательской деятельности.

1. Организационный момент

Постановка целей и задач урока.

2. Проверка домашнего задания

№10.17 (Задачник 9кл. А.Г. Мордкович).

а) у = f(х), f(х) =

0,4
4. f(х) 0 при х 0,4 ; f(х) х 0,4.
5. Функция возрастает при х € [– 2; + ∞)
6. Функция ограничена снизу.
7. у_наим = – 3, у_наиб не существует
8. Функция непрерывна.

(Вы использовали алгоритм исследования функции?) Слайд.

2. Таблицу, которую вам задавалась, проверим по слайду.

Координаты точек пересечения графика с Оу

( 0;)

( 0;)

( 0;)

3. Актуализация знаний

– Даны функции.
– Указать область определения для каждой функции.
– Сравнить значение каждой функции для каждой пары значения аргумента: 1 и – 1; 2 и – 2.
– Для каких из данных функций в области определения выполняются равенства f(– х) = f(х), f(– х) = –f(х)? (полученные данные занести в таблицу) Слайд

1. f(х) =

5. f(х) =

6. f(х)=

и 0

и не опред.

– Выполняя данную работу, ребята мы выявили ещё одно свойство функции, незнакомое вам, но не менее важное, чем остальные – это чётность и нечетность функции. Запишите тему урока: «Чётные и нечётные функции», наша задача – научиться определять чётность и нечётность функции, выяснить значимость этого свойства в исследовании функций и построении графиков.
Итак, найдём определения в учебнике и прочитаем (стр. 110). Слайд

Опр. 2 Функция у = f (х), заданная на множестве Х называется нечётной, если для любого значения хЄ Х выполняется равенство f(–х)= –f(х). Приведите примеры.

Изучение вопроса о том, является ли функция чётной или нечётной называют исследованием функции на чётность. Слайд

В определениях 1 и 2 шла речь о значениях функции при х и – х, тем самым предполагается, что функция определена и при значении х, и при – х.

Опр 3. Если числовое множество вместе с каждым своим элементом х содержит и противоположный элемент –х, то множество Х называют симметричным множеством.

(–2;2), [–5;5]; (∞;∞) – симметричные множества, а [0; ∞), (2;–2], [–5;4] – несимметричные.

– У чётных функций область определения – симметричное множество? У нечётных?
– Если же D(f) – несимметричное множество, то функция какая?
– Таким образом, если функция у = f(х) – чётная или нечётная, то её область определения D(f) – симметричное множество. А верно ли обратное утверждение, если область определения функции симметричное множество, то она чётна, либо нечётна?
– Значит наличие симметричного множества области определения – это необходимое условие, но недостаточное.
– Так как же исследовать функцию на четность? Давайте попробуем составить алгоритм.

Алгоритм исследования функции на чётность

1. Установить, симметрична ли область определения функции. Если нет, то функция не является ни чётной, ни нечётной. Если да, то перейти к шагу 2 алгоритма.

2. Составить выражение для f(– х).

если f(– х) ≠ f(х) и f(– х) ≠ –f(х), то функция не является ни чётной, ни нечётной.

Исследовать на чётность функцию а) у = х 5 +; б) у = ; в) у= .

а) h(х) = х 5 +,

1) D(h) = (–∞; 0) U (0; +∞), симметричное множество.

2) h (– х) = (–х) 5 + – х5 –= – (х 5 +),

3) h(– х) = – h (х) = функция h(х) = х 5 + нечётная.

б) у = ,

у = f(х), D(f) = (–∞; –9)? (–9; +∞), несимметричное множество, значит функция ни чётная, ни нечётная.

в) f(х) = , у = f (х),

1) D(f) = (–∞; 3] ≠ [3; +∞), симметричное множество.

2)f (– х) == ;

3) f (– х) = f (х) = функция f(х) = чётная.

Итак, по аналитической записи можно определить четность функции? Но кроме аналитического способа задания функции есть другие. Какие? Можно ли по графику функции выявить её четность? Давайте вернёмся к заданию, которое мы выполняли в начале урока, найдём соответствие между аналитически заданными функциями и их графиками (изображёнными на доске), что вы находите примечательного в расположении графиков чётных функций? Нечётных?

График чётной функции симметричен относительно оси у.

График нечётной функции симметричен относительно начала координат.

– Верны ли обратные утверждения?

Если график функции у = f(х) симметричен относительно оси ординат, то у = f(х) – чётная функция.

Если график функции у = f(х) симметричен относительно начала координат, то у = f(х) – нечётная функция.

Доказательство данных утверждений разобрать дома самостоятельно по учебнику и записать в тетрадь.

5. Первичное закрепление

1. Является ли симметричным заданное множество: а) [–7;7]; б) (∞; –2), (–4; 4]?

2. Исследуйте на чётность функцию:
а) ; б) у = х· (5 – х 2 ).

2. Исследуйте на чётность функцию:

а) у = х 2 · (2х – х 3 ), б) у =

3. На рис. построен график у = f(х), для всех х, удовлетворяющих условию х? 0.
Постройте график функции у = f(х), если у = f(х) – чётная функция.

Источник

Осевая и центральная симметрия

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах на 8 марта.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 2. Постройте треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра (точки О).

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Источник

Диаграммы Эйлера-Венна

Что такое диаграммы Эйлера-Венна

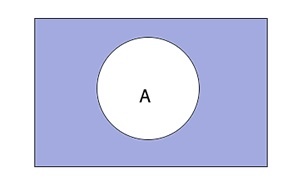
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.

Для отражения отношений между множествами математики Джон Венн и Леонард Эйлер использовали для способа. Если Венн использовал для обозначения множеств замкнутые фигуры, то Эйлер использовал круги.

Диаграммы Эйлера-Венна являются важным частным случаем кругов Эйлера. Диаграммы изображают все 2^n комбинаций n свойств, что является конечной булевой алгеброй. В случае n = 3 диаграмма Эйлера-Венна обычно состоит из трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приближенно равным длине стороны треугольника.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Принцип построения

Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.

Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.

С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:

Дополнение множества

При этом не все элементы, не являющиеся элементами А, могут быть включены в \(\overline A.\) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение \overline A определяется следующим образом:

Таким образом выглядит дополнение \(\overline A\) графически:

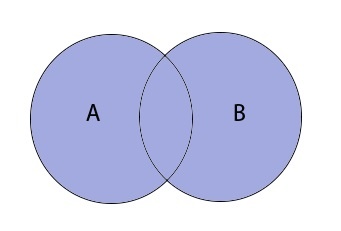
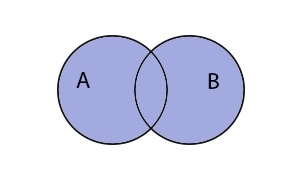
Объединение множеств

Объединение записывается следующим образом:

Таким образом объединение множеств выглядит графически:

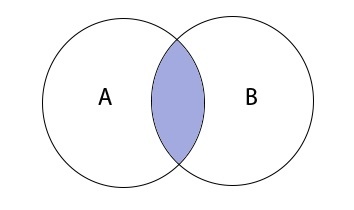
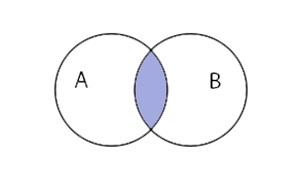
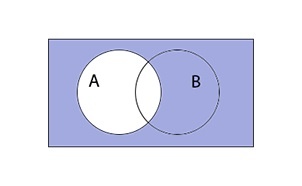
Пересечение множеств

Пересечение множеств записывается следующим образом:

Таким образом пересечение множеств выглядит графически:

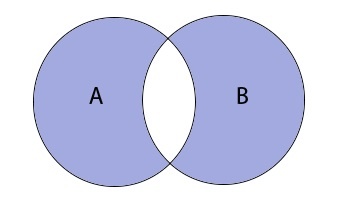
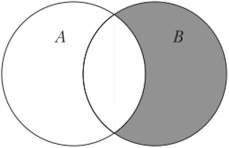
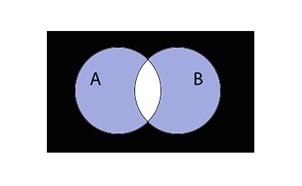
Симметричная разность множеств

Симметричная разность A \ B — это такое множество, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество

Разность множеств записывается следующим образом:

\(A\bigtriangleup B=(A\backslash B)\cup(B\backslash A)\)

Таким образом разность выглядит графически:

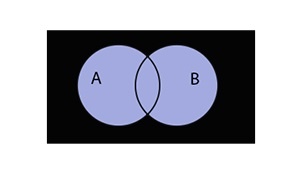
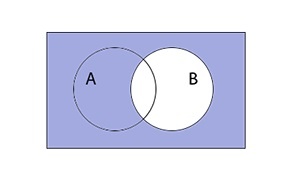
Разность множеств

Разностью A \ B является множество элементов A, не входящих в B.

Разность множеств записывается следующим образом:

Таким образом разность выглядит графически:

Использование диаграмм Эйлера-Венна для доказательства логических равенств

Рассмотрим, как диаграммы Эйлера-Венна применяются для доказательства логических равенств.

Предположим, что перед нами конъюнкция множеств \(A\;\wedge\;B\)

В первую очередь обратим внимание на левую часть равенства. Построим диаграмму для множеств А и B. Графически отметим дизъюнкцию, заштриховав оба круга цветом.

Теперь отобразим инверсию, заштриховав область за пределами множеств.

Обратим внимание на правую часть равенства. В первую очередь отобразим инверсию A штриховкой область за пределами круга множества A цветом.

Проведем аналогичную операцию с множеством B.

Теперь штриховкой черным цветом всех областей пересечения отобразим конъюнкцию инверсий множеств А и B.

При сравнении области для отображения правой и левой частей, становится очевидно, что они равны. Справедливость логического равенства доказана с помощью диаграммы Эйлера-Венна.

Примеры задач с решением

Задача

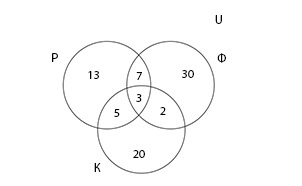
Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?

Решение

В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.

Необходимо найти \(n(Р\;\cup\;Ф\;\cup\;К)\;=\;n\;(U\;\backslash\;(Р\;\cap\;Ф\;\cap\:К))\)

В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна. Составляя ее, важно помнить, что если в \(Р\;\cap\;Ф\;\cap\:К\) три элемента, а в множестве \(Р\;\cap\;Ф\) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено.

Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.

Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:

Ответ: 20 туристов не побывали ни в одном из указанных заведений.

Задача

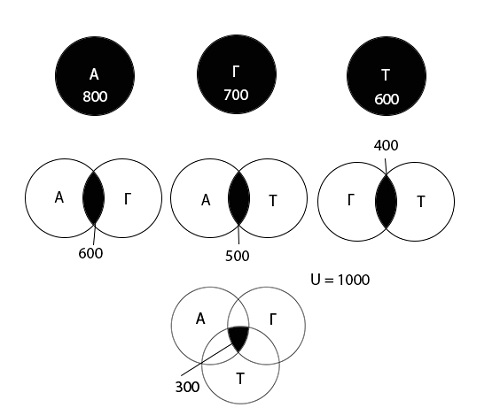
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?

Решение

Начнем с определения множеств и введения обозначений. В данном случае, их три:

Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.

Теперь используя диаграмму, обозначим область, которую необходимо найти:

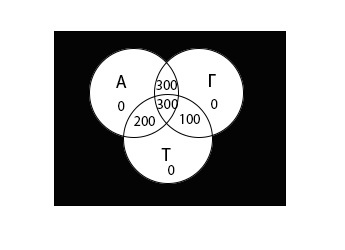
Определим количество школьников для всех возможных областей.

Обозначим искомую область А = 0, Г = 0, Т = 0 как «х».

Найдем остальные области:

Теперь внесем значения всех областей в диаграмму:

\((A\;\cup\;Г\;\cup\;Т)\;=\; 0 + 0 + 0 + 300 + 300 + 200 + 100 = 900\)

Ответ: 100 школьников не решило ни одной задачи.

Источник