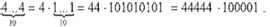что такое семизначное число

Семизначное число это сколько

Ответ или решение 1

Нам нужно узнать сколько всего существует семизначных цифр.

Для того, чтобы узнать это, нам нужно от самого максимального семизначного числа отнять самое минимальное семизначное число, в ответе мы получим количество цифр.

Вспомним эти числа.

Максимальное семизначное число — 9.999.999.

Минимальное семизначное число — 1.000.000.

9999999 — 1000000 = 8999999.

Ответ:8.999.999 существует семизначных цифр.

Сколько существует семизначных чисел без нуля в записи, у которых все цифры повторяются хотя бы дважды?

задан 4 Ноя ’17 7:24

1 ответ

Прежде всего, рассмотрим все варианты представления числа 7 в виде суммы слагаемых, каждое из которых не меньше двух. Таких вариантов немного: 7, 5+2, 4+3, 3+2+2. Для каждого из них подсчитаем количество чисел, а затем всё сложим.

Что ты хочешь узнать?

Ответ

Ответ:

2187 семизначных чисел

Пошаговое объяснение:

Х₁ Х₂ Х₃ Х₄ Х₅ Х₆ Х₇ — семизначное число

Х может быть 3, 7 или 9, следовательно, цифры в семизначном числе могут повторятся

Например: 7777777; 3377997

Первую цифру Х₁ семизначного числа можно выбрать тремя способами (так как выбираем из чисел 3, 7, 9),

вторую цифру — Х₂ семизначного числа можно выбрать тремя способами (выбираем из чисел 3, 7, 9 и они могут повторятся)

третью цифру — Х₃ семизначного числа можно выбрать тремя способами (выбираем из чисел 3, 7, 9)

четвертую цифру — Х₄ семизначного числа можно выбрать тремя способами (выбираем из чисел 3, 7, 9)

пятую цифру — Х₅ семизначного числа можно выбрать тремя способами (выбираем из чисел 3, 7, 9)

шестую цифру — Х₆ семизначного числа можно выбрать тремя способами (выбираем из чисел 3, 7, 9)

седьмую цифру — Х₇ семизначного числа можно выбрать тремя способами (выбираем из чисел 3, 7, 9)

По правилу умножения (известное в комбинаторике правило) умножаем все способы для выбора цифр,

получаем 3*3*3*3*3*3*3 = 2187 семизначных чисел.

Источник

Какое самое наибольшее семизначное число?

Ответы:

Самое наибольшее семизначное целое число это число, которое состоит из семи девяток, а точнее это

Самым большим семизначным числом будет 9. 999. 999 (девять миллионов девятьсот девяносто девять тысяч девятьсот девяносто девять), потому что следующее число будет 10. 000. 000 (десять миллионов), а оно уже имеет восемь знаков.

Вопрос из области математики, которую я очень любила в школе.

Семизначное число- это уже миллионы.

Самый маленький разряд-это единицы, затем десятки, сотни и т.д

Поэтому самым наименьшем семизначным числом будет 1 000 000.

Самым наибольшим семизначным числом будет 9 999 999.

Попробуем найти наибольшее семизначное число:

Можно найти самое наибольшее семизначное число еще и другим способом:

возьмем самое наименьшее восьмизначное число (10 000 000) и вычтем из него единицу (1), и получим самое наибольшее семизначное число, то есть:

Самая большая цифра (одна) это девятка.

Семизначное число значит цифр в нём семь.

Соответственно семь подряд девяток и будут тем самым самым большим семизначным числом.

Если прописью (словами), то это девять миллионов, девятьсот девяносто девять тысяч девятьсот девяносто девять.

На самом деле на вопрос ответить не сложно, ведь семизначное число это то, которое состоит из семи знаков.

Следовательно, таковым является 9999999 (девять миллионов девятьсот девяносто девять тысяч девятьсот девяносто девять).

Источник

ЗАМЕЧАТЕЛЬНЫЕ «СМИТЫ»

Кандидат педагогических наук Наталья КАРПУШИНА.

История науки знает немало примеров случайных открытий. Кто не слышал предание о том, как Архимед, принимая ванну, открыл закон о телах, погружённых в жидкость, или байку о Ньютоне, который, наблюдая за падением с дерева яблока, создал теорию тяготения? Сколько раз пытливые умы находили источник озарения в живой природе! А как много блестящих идей посетили учёных во сне! Д. И. Менделееву приснилась его периодическая таблица элементов, а Ф. Кекуле — структурная формула бензола. Но иногда важное открытие, сделанное специалистом, запоминается куда меньше, чем нехитрая закономерность, подмеченная человеком, вовсе её не искавшим, да и вообще далёким от науки. Каким-то непостижимым образом та находит его сама. И чем необычнее обстоятельства, сопутствующие этому событию, тем более яркое впечатление оно производит.

Невероятное везение профессора Смита

Один из примечательных случаев такого рода произошёл четверть века назад с любителем чисел, наблюдательным профессором психологии Гарольдом Смитом, которому (безо всякого преувеличения) крупно повезло: он сумел войти в историю математики, не имея к ней, в сущности, никакого отношения. А счастливым для Смита оказался. номер собственного телефона! Как-то профессор заметил, что этот номер, выражающийся составным семизначным числом 4 937 775, обладает любопытным свойством — сумма цифр номера равна сумме цифр всех его простых делителей:

4 937 775 = 3 · 5 · 5 · 65 837,

4 + 9 + 3 + 7 + 7 + 7 + 5 = 42,

3 + 5 + 5 + 6 + 5 + 8 + 3 + 7 = 42.

Быть может, этот факт так и остался бы в разряде числовых курьёзов, не вмешайся в историю родственник Смита — математик, профессор одного из американских университетов Альберт Виланский. Он опубликовал в 1982 году заметку об обнаруженном свойстве, а обладающие им составные числа назвал именем Смита. Тогда же Виланский предположил, что таких чисел существует бесконечно много. И оказался прав: вскоре эту гипотезу доказал его коллега. Так было положено начало исследованию весьма интересного множества чисел.

Самое удивительное, что изучение чисел Смита, или просто «смитов», началось с семизначного (!) числа, но ещё поразительнее то, что их не открыли гораздо раньше. Даже любой школьник знает: 2 + 2 = 4, и это никакой не курьёз!

Диковинки среди Смитов

Числа Смита обладают многими замечательными свойствами. Мы не станем на них останавливаться, заметим только, что смиты тесно связаны с другими известными математикам числами, через которые могут выражаться: репьюнитами (они записываются с помощью одних единиц) и простыми числами Мерсенна.

В семействе смитов найдётся немало настоящих диковинок! Одни числа отличаются красивым сочетанием цифр: 654, 44733, 67067. Другие — их повторяемостью: 666, 1111, 4444444444. Третьи — симметрией записи (палиндромностью): 3663, 22522, 864468. А разве не радует глаз разложение некоторых смитов на множители?

3663 = 3 · 1221 = 33 · 111,

864468 = 2 · 432234 = 111 · 7788,

К изюминкам множества смитов можно смело отнести и десятизначные числа, у которых все цифры различные. Укажем наименьшее и наибольшее из них:

1 023 465 798 и 9 876 542 103.

А вот семизначное число 1 346 269 привлекает внимание тем, что это самый маленький смит, встречающийся в знаменитой последовательности Фибоначчи (31-й её член). Не редкость смиты и среди так называемых фигурных чисел, учение о которых восходит ещё к пифагорейцам. Так, смит 121 — квадратное число, 378 — треугольное, а 22 — пятиугольное.

Кроме того, во множестве смитов имеются примечательные пары чисел, отличающихся друг от друга всего на 1. Вероятно, по аналогии с числами-близнецами (простыми числами, отличающимися на 2), их прозвали братьями смита. Наименьшую такую пару составляют числа 728 и 729. Для примера именно она выбрана потому, что каждый из «братьев» интересен сам по себе: первый — сумма двух смитов, второй — квадрат смита:

то есть они оба порождены числами Смита.

Надо сказать, некоторые члены этого семейства образуются из других его представителей более простыми путями. Иногда бывает достаточно записать рядом (без пробела) два смита. Таким способом из чисел 22 и 27 получаются четырёхзначные числа Смита 2227 и 2722. В ином случае в запись исходного смита-палиндрома добавляются нули. Например, числа 22 и 535 порождают смиты 202 и 50305. Нередко нужный результат достигается простой перестановкой цифр (как в тройке смитов 319, 391, 913) или благодаря симметрии их расположения, приводящей к повтору цифр в образующихся числах (454, 45454, 454454).

В этом удивительном множестве выделяют также числа, у которых сумма цифр выражается числом Смита. Им даже дали собственное название — суперчисла Смита. Таким свойством обладают, к примеру, числа 202 (2 + 0 + 2 = 4) и 778 (7 + 7 + +8 = 22).

Особо ценятся среди смитов рекордсмены по числу цифр, присутствующих в их записи. К ним относится, в частности, исполин

где 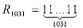— наибольший из известных простых репьюнитов.

В этом числе Смита насчитывается 107 060 074 цифры! С трудом верится — так компактно оно «упаковано» с помощью степеней. А знаете, сколько времени потребовалось бы, чтобы записать это число полностью? Даже при непрерывной работе с высокой скоростью письма 90 цифр в минуту на это ушло бы 2 года и 3 месяца!

В книге М. Гарднера «От мозаик Пенроуза к надёжным шифрам» приведён магический квадрат третьего порядка, составленный из чисел Смита (рис. 1). Его магическая постоянная равна 822 и является, по словам автора, наименьшей из возможных для такого квадрата.

Все указанные в клетках числа — чётные. Разделив каждое из них на 2, получим новый магический квадрат с постоянной (суммой чисел в каждой строке, каждом столбце и на диагоналях), равной 411 (рис. 2). Примечателен он тем, что состоит из девяти простых чисел; согласитесь, неплохое наблюдение автора. Но если бы дело было только в обнаруженном им свойстве… Ведь известны и другие магические квадраты, составленные из простых чисел. Однако нас сейчас интересуют вовсе не они, а числа Смита. Какое отношение имеют они к получившейся таблице?

Приглядитесь внимательнее, и вы заметите, что суммы некоторых её чисел дают числа Смита. Так, в простейшем случае

Разность магической постоянной 411 и числа 137 из центральной клетки равна другому представителю семейства смитов — числу 274. Это означает, что сумма любых двух простых чисел, занимающих центрально-симметричные клетки квадрата, оказывается числом Смита:

11 + 263 = 83 + 191 = 47 + 227 = 101+ + 173 = 274.

А вот ещё один любопытный факт: суммы пар чисел, стоящих вдоль линий, параллельных главным диагоналям, также равны числам Смита. Действительно:

11 + 83 = 94, 83 + 263 = 346,

263 + 191 = 454, 191 + 11 = 202.

Все пять смитов есть в исходной таблице и, что характерно, красиво располагаются в её угловых клетках и в центре (рис. 1), в то время как сами слагаемые размещаются в средних клетках по сторонам второй таблицы (рис. 2). Если собрать все девять чисел в новую таблицу (рис. 3), они образуют двойной симметричный узор (рис. 4).

К тому же теперь наглядно видно, как просто и разумно связаны между собой тройки чисел, входящих в каждое из четырёх последних равенств (рис. 5, 6).

Можно также рассматривать суммы трёх или более чисел второго квадрата, при выборе которых логично руководствоваться симметрией их расположения — к примеру, относительно главной диагонали. Возьмём для определённости диагональ квадрата, идущую из левого нижнего в правый верхний угол. Она даёт три числа: 101, 137 и 173. Добавим к ним ещё четыре: 47, 263, 227 и 83 (рис. 7).

Оказывается, их различные комбинации приводят к разным числам Смита. Скажем, каждая из троек 47, 263, 173 и 227, 83, 173 при сложении даёт 483.

47 + 263 + 173 = 227 + 83 + 173 = 483.

Весьма любопытная картина вырисовывается при игре с четвёрками чисел. Легко заметить, что смит 483 получается также при сложении 346 и 137 (оба числа встретились в рассмотренных магических квадратах, рис. 1 и 2). Тогда смит 346 можно представить в виде разности 483 и 137:

(47 + 263 + 173) – 137 = (227 + 83 + +173) – 137 = 346.

Аналогично 483 = 382 + 101, откуда 382= 483 – 101, или (47 + 263 + 173) – 101 = (227 + 83 + 173) – 101 = 382.

Пойдём дальше: 274 = 411 – 137, где 411 есть магическая постоянная второго квадрата, а значит, выполняются равенства

(47 + 263 + 101) – 137 = (227 + 83 + 101) – 137 = 274.

Итак, задействовав возможные пары чисел главной диагонали этого квадрата, удалось «сконструировать» три числа Смита, присутствующие в исходном квадрате: 346, 382 и 274. И если в первый раз такой результат мог быть случайностью, а во второй — простым совпадением, то в третий раз начинает проявляться вполне определённая закономерность. А какой истинный любитель математики откажется её проверить?

Если теперь ограничиться рассмотрением чисел 47, 263, 83 и 227, нетрудно получить хотя и не столь очевидные, но уже вполне ожидаемые и даже предсказуемые результаты:

227 + 83 – 263 + 47 = 94,

227 + 83 – 47+263 = 526,

47 + 263 – 227 + 83 = 166,

47 + 263 – 83 + 227 = 454.

И вот перед нами ещё четыре смита из исходного квадрата. Любопытно, что они занимают такие же клетки, что и числа второго квадрата, из которых получены. Мозаика почти сложилась, осталось всего ничего — выразить ещё два смита: 22 и 202. А в том, что эта задача разрешима, сомнений не осталось.

Воспользуемся тем, что уже известно. Ближайший к числу 22 смит из составленного Гарднером магического квадрата — число 94; 22 = 94 – 72, или (227 + 83 – 263 + 47) – (173 – 101) = 22.

Аналогично 202 = 166 + 36, или (47 + 263 – 227 + 83) + (173 – 137) = 202. Впрочем, в этом случае можно обойтись и четвёркой чисел: 202 = 303 – 101 = 47 + 83 + 173 – 101.

Между тем попытки выразить аналогичным образом число 22 приводят к ещё одному открытию: оказывается, смиты из исходной таблицы можно получить из четвёрок чисел, занимающих соседние центрально-симметричные клетки второй таблицы (рис. 8), например:

58 – 36 = (47 + 11) – (263 – 227) = 22,

58 + 36 = (47 + 11) + (263 – 227) = 94,

(173 + 83) – (191 – 101) = 166,

(173 + 83) + (191 – 101) = 346.

Получается изящная головоломка: как, имея набор простых чисел, составить простейший магический квадрат из составных чисел Смита, да ещё и с наименьшей постоянной?

Такие простые закономерности…

Поразмышляв немного, вы обнаружите и, возможно, обоснуете немало интересных закономерностей, связывающих числа Смита. А начать можно с чего-нибудь совсем простого.

Скажем, 58 – 36 = 22, а 58 + 36 = 94, откуда 58 = (22 + 94) : 2, следовательно, смит 58 — среднее арифметическое смитов 22 и 94. В свою очередь 94 — среднее арифметическое 22 и 166, а вот число 22 — среднее геометрическое смитов 4 и 121 (22 =2 · 11 = ).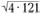

Или другой пример. Выпишем по порядку первые пятнадцать чисел Смита и выделим из них каждое второе:

Посмотрите, как интересно они связаны:

22 = 265 – 1 · 3 5 = 319 – 11 · 3 3 = 355 – 111 · 3.

А вот ещё одно наблюдение. Оно касается многозначных чисел Смита, у которых всего два простых множителя.

22 = 2 · 11 = 22 + 0, 2 + 1 + 1 = 2 + 2 + 0 = 4,

58 = 2 · 29 = 22 + 36, 2 + 2 + 9 = 2 + 2 + 3 + 6 = 13,

85 = 5 · 17 = 22 + 63, 5 + 1 + 7 = 2 + 2 + 6 + 3 = 13,

94 = 2 · 47 = 22 + 72, 2 + 4 + 7 = 2 + 2 + 7 + 2 = 13.

Как видим, если такое число представить в виде суммы двух слагаемых, причём одно из них 22 (смит), то сумма цифр его множителей будет такой же, как и сумма цифр слагаемых, и равна либо 4, либо 13.

Оказывается, аналогичным свойством обладают и трёхзначные числа Смита, при этом повторяется слагаемое 202 (снова смит!), а суммы цифр равны 4, 13 или 22. Например:

355 = 5 · 71 = 202 + 153 (суммы цифр — 13),

778 = 2 · 389 = 202 + 576 (суммы цифр — 22).

Любопытно также, что у всех ключевых чисел (4, 13, 22, 202) сумма цифр равна наименьшему смиту, а два из них (22 и 202) — суперчисла Смита.

Можно изучать самые разные группы смитов и даже отдельных представителей этого семейства, открывая всё новые и новые их свойства. Чем, например, примечательна тройка 27, 58 и 85? Что общего у чисел 4, 121 и 10 201? А какое отношение к смитам имеет число 31? Как говорил в таких случаях один из героев Гарднера, не существует ни одного числа, которое не обладало бы какими-нибудь необычными свойствами. И представители многочисленного семейства смитов лишь подтверждают это.

Репьюниты (от англ. repeated unit — повторенная единица) — натуральные числа, в записи которых присутствуют только единицы: то есть R₁ = 1, R₂ = 11, R₃ = 111 и т. д., в общем виде R_n = (10_n – 1) : 9, где n = 1, 2, 3… — числа натурального ряда.

Простые числа Мерсенна — простые числа вида M_p = 2 p – 1, где p также простое число 2, 3, 5, 7, 13, 17, 19, 31… (М₁₁ простым не является). Вероятно, самое большое известное простое число Мерсенна — М₂₁₆₀₉₁ имеет 65 050 цифр.

Ряд Фибоначчи — числовой ряд 1, 1, 2, 3, 5, 8, 13, 21… каждый последующий член которого равен сумме двух преды- дущих: A_n = A_n–1 + A_n–2. Ряд интересен тем, что отношение двух соседних членов ряда в пределе даёт «золотое сечение» — отношение частей поделённого отрезка 0,62 : 0,38. Например, уже 13 : 21= = 0,619 ≈ 0,62.

Источник

Формула вселенского Созидания – семизначное число!

 17.10.2007 01:05 Обновлено 15.05.2011 14:24 Автор: Пьянов В. И.

Виктор Пьянов

(по материалам ОТКРЫТОГО ПИСЬМА А. ГОРДОНУ от 2004 г.)

Формула вселенского Созидания – семизначное число!

ФОРМУЛА ТОТА.

Поэтому можно сказать, что семизначное число No, вычисляемое по формуле, содержащей семь целочисленных коэффициентов [1], лежит в основе всего сущего во Вселенной.

Все существующее в мироздании действительно РОЖДАЕТСЯ И СОЗИДАЕТСЯ действием физических законов как бы из этого числа.

А высокоразвитые внеземные цивилизации могли считать эту формулу (формулу созидания) и само число No (число созидания), как одно из высших достижений разума, достойными для передачи развивающимся цивилизациям.

Можно показать, что некоторые из этих чисел и их комбинаций являются коэффициентами или разложениями семи целочисленных коэффициентов формулы для вычисления «числа созидания» No.

Изложенное в настоящем письме доказывает, что тысячи лет назад заключенное в числах Абсолютное Знание в закодированном, непонятном для непосвященных виде было различными способами дано людям для расшифровки.

Это часть интеллектуальной игры, которую вело и ведет с человечеством Мировой разум.

22.01.97 г. я выступил в Русском географическом обществе с докладом «От палеоконтактов к расчету мировых констант», в котором изложил разработанную мною гидродинамическую вихревую теорию строения материи и устройства мироздания, гипотезу о контактах древних греков с инопланетянами, передававшими им знания и гипотезу о тайном смысле «Чуда в Фатиме» [3].

Из теории следует, что первичными «кирпичиками» мироздания являются мюонные нейтрино, а относительные массы всех стабильных элементарных частиц выражаются через количество No мюонных нейтрино в электроне.

Численное значение No = 1881302.

Присутствовавший на докладе корреспондент “Известий” опубликовал в своей газете заметку о моем выступлении, в которой он назвал полученную мною формулу для вычисления No “формулой созидания”.

Девять лет назад я считал, что древнегреческие философы, чьи идеи два с половиной тысячелетия служат неиссякаемым источником истинного знания, получили это знание от внеземных цивилизаций [1].

Поэтому можно сказать, что семизначное число No, вычисляемое по формуле, содержащей семь целочисленных коэффициентов [1], лежит в основе всего сущего во Вселенной.

Все существующее в мироздании действительно РОЖДАЕТСЯ И СОЗИДАЕТСЯ действием физических законов как бы из этого числа.

А высокоразвитые внеземные цивилизации могли считать эту формулу (формулу созидания) и само число No (число созидания), как одно из высших достижений разума, достойными для передачи развивающимся цивилизациям.

Многие ученые, изучающие историю человечества, отмечают, что некоторые числа и их комбинации с удивительным постоянством повторяются в мифах и календарных системах разных народов.

Повторяются они также в священных писаниях различных религий, в архитектуре культовых сооружений древних цивилизаций, в ритуалах некоторых тайных обществ и в различного рода древних поверьях.

Можно показать, что некоторые из этих чисел и их комбинаций являются коэффициентами или разложениями семи целочисленных коэффициентов формулы для вычисления «числа созидания» No.

Изложенное в настоящем письме доказывает, что тысячи лет назад заключенное в числах Абсолютное Знание в закодированном, непонятном для непосвященных виде было различными способами дано людям для расшифровки.

Это часть интеллектуальной игры, которую вело и ведет с человечеством Мировой разум.

После того, как я обнаружил [3], что во временных характеристиках шести явлений Фатимской Богоматери в 1917 году в Португалии закодированы семь целочисленных коэффициентов формулы для вычисления No (в том числе 666 и 13, вызывающие мистический ужас у христиан).

Я не сомневался, что само число созидания No, которое постановкой точек преобразуется в дату 1881.3.02, закодировано в таком же необычном, как Чудо в Фатиме, событии 1881 года.

В моей памяти тогда были даты двух связанных с мистикой событий 1881 года.

В первый день марта 1881г. (1881.3.01) в России был убит Царь-Освободитель Александр II. Это убийство подтверждает существование феномена сбывающихся пророчеств. Оно, также как и убийство 17.7.1918 г. последнего из царей династии Романовых Николая II было предсказано монахом Авелем задолго до этих событий.

В последний день февраля 1881 года (1881.28.2) “Тексты пирамид” впервые увидел ученый – французский египтолог Гастон Масперо.

Согласно документальным отчетам путь к погребальной камере пирамиды Унаса, стены которой от пола до потолка оказались расписанными тысячами иероглифов, показал шакал.

В Древнем Египте поклонялись двум богам с головами шакалов, Анубису и Упуату.

Кажется, что есть что-то мистическое в том, что путь к древним текстам указал шакал, а имена богов, чьими символами служили шакалы, в переводе означают “Хранитель священных писаний” и “Открыватель путей”.

В уже неоднократно мною цитированной книге Хэнкока приводится краткое содержание одного из разделов мифа об Осирисе в изложении Э. А. Уоллис-Баджа, бывшего хранителя египетских древностей в Британском музее:

«Богиню Нут, супругу бога Солнца Ра,

Когда Ра раскрыл эту интригу,

он выбранил жену и провозгласил,

что она не сможет родить

ни в один из месяцев года.

Тогда бог Тот, который тоже питал к Нут

нежные чувства, выиграл у Луны пять дней,

которые присоединил к 360 дням, из которых

в то время состоял год.

В ПЕРВЫЙ ЖЕ (выделено мною В. П.) из этих пяти

дней был рожден Осирис;

в момент его рождения некий голос провозгласил,

что родился бог созидания”.

Необходимо, наверное, напомнить, что по религиозным верованиям древних египтян Нут – богиня Неба и матерь всех звезд, Геб – бог Земли, а бог мудрости Тот одновременно считался и богом Луны.

Действующие лица мифа отражают космические тела, определяющие значения характеристик прецессионного движения Земли.

Во-первых, это сама Земля, во-вторых, Солнце, притяжение которого определяет длительность года, выраженную в земных сутках и влияет на период прецессии, в-третьих, Луна, притяжение которой в основном и определяет период прецессии, в-четвертых, небо, на звездном фоне которого можно наблюдать прецессию точек равноденствий.

Число 361, как порядковый номер дня рождения (27.12), служит идентификатором Осириса.

Наличие чисел и описание арифметических действий в мифе о рождении Осириса, повествующем о биологических процессах, позволяет предположить, что в нем закодирована числовая загадка, а перечень персонажей мифа указывает на то, что загадка каким-то образом связана с периодом прецессии земной оси.

В своей книге Г. Хэнкок пишет, что археоастроном Джейн Б. Селлерс выдвинула гипотезу, согласно которой в мифе об Осирисе были сознательно заложены исходные данные для расчета прецессии равноденствий.

По проведенным ею расчетам закодированный в мифе период прецессии равен 25920 лет.

На момент прочтения выше процитированного изложения мифа о рождении Осириса у меня уже не было сомнений, что Тоту, которого древние египтяне называли Измерителем Земли, было известно точное значение периода прецессии земной оси – 25776 лет.

Я предположил, что именно это число зашифровано в изложении мифа о рождении бога созидания.

Кроме этого, на момент прочтения я твердо знал, что Бог – выраженное в числах Абсолютное Знание, что Бог – Число (см. Раздел 3.), а про себя называл число N0 (1881302) числом созидания.

Так как итогом манипуляций Тота с числами стало рождение бога (числа) созидания, то несложно было догадаться, что в результате решения (раскодирования) числового ребуса должно получиться число созидания N0, а при решении нужно производить арифметические действия и использовать числа, указанные в мифе (5, 360) и значение периода прецессии.

Очевидно, что один из самых простых вариантов кодировки – разложить число на множители и сделать множители частями кода. Посмотрим, как это можно выполнить с числом 1881302.

В полученном результате число 25423 сопоставимо по величине с приближенным значением периода прецессии равноденствий – числом 25920, указанным госпожой Селлерс, а число 370 сопоставимо с длительностью года. Так как 25423 25920.

Рассмотрим третий вариант (посреднему):

В разложении посреднему число 365 на 5 больше 360, а, без учета дробной части, 25771 меньше, чем известное (Г. Хэнкок) в современной астрономии значение периода прецессии 25776 также на 5. Вариант очень удобный для кодирования в мифе: во-первых, и 365, и 25776 численно равны временным характеристикам движения Земли, а во-вторых, можно обыграть одинаковую разность между парами 365-360 и 25776-25771.

Проведенный анализ вариантов кодирования числа созидания No и содержание мифа свидетельствуют, что Тот проводил аналогичный анализ разложения числа 1881302 и знал, с какой точностью будут знать значение периода прецессии земной оси современные нам астрономы.

В работе [1] приведены полученные мною расчетные уточненные значения физических и космологических мировых констант.

До расшифровки сценария Тота я испытывал удовлетворение от выполненной работы. В процессе расшифровки я стал осознавать, что особых оснований гордиться у меня нет, как робот я выполняю то, на что запрограммирован.

В силу единства Природы все мировые константы уравнениями физики связаны между собой и каждая со всеми.

Период прецессии земной оси является одной из космологических констант и в последнем из приведенных разложений мировой константы No связан со значением No арифметическим равенством, не имеющим никакого отношения к физике.

Не исключено, что число 25776,26027, «явившееся» из разложения числа созидания No и мифа о рождении бога созидания, представляет собой данное мне таким образом уточненное значение периода прецессии.

С учетом этого предположения поступим так, как действовал Тот в мифе. Отнимем от уточненного значения периода прецессии число 5 и прибавим 5 к 360 (длительности года).

Так как в мифе речь идет об умножении числа богов, а Тота называли Умножителем времени, перемножим полученные числа, а затем разделим произведение на 5 (в мифе говорится, что Осирис был рожден в один из пяти дней), как это подсказывает разложение числа No:

Говоря Тот, я каждый раз имею в виду Мировой Разум, управляющий движением материи во Вселенной, поэтому нет ничего удивительного в том, что обладатель Абсолютного Знания Демиург, сотворивший все на основе предварительного числового сценария и, в том числе, Землю и окружающие ее небесные тела, знал значение No и будущий период прецессии замышленной им планеты Земля.

Осуществим те же действия Тота с известным астрономам значением периода прецессии:

Полученный результат меньше, чем 1881302 на 19. По буквенно-цифровому шифру Тота число 19 представляет собой аббревиатуру АЗ слов Абсолютное Знание.

То есть число 1881283, в отличие от 1881302, – это ещё не Абсолютное Знание. Шифр Тота позволяет узнать, что же закодировано в этом числе.

В соответствии с шифром произведем в числе 1881283 замену 3 на 2 и поставим точки – 1881.28.2.

Полученная дата является датой открытия “Текстов пирамид” – 28 февраля 1881г., последним днем второго месяца 1881г. Удивительный результат!

В древнейших “Текстах пирамид” в мифе о рождении бога созидания была закодирована дата открытия самих Текстов будущими поколениями. Когда наступил сценарный момент, шакал Упуату указал путь к священным писаниям.

В древнеегипетском и древнерусском календарях год состоял из 12 месяцев по 30 дней, к которым в конце года прибавляли 5 дополнительных дней.

Последний день второго месяца может в этих календарях быть обозначен как 30.2, что при удалении точек и в совокупности с современным обозначением года открытия “Текстов пирамид” вновь приводит к числу созидания 1881302. Это число является закодированным обозначением даты открытия “Текстов пирамид”.

Обобщая полученные результаты, можно заключить, что произведение 1/5 приблизительного значения периода прецессии (значение 25776 лет, по сравнению с точным значением 25776,26027 является одним из таковых) на календарную длительность года (различную в отличающихся календарных системах) позволяет получать даты событий.

Пятая часть приблизительного значения периода прецессии может колебаться в некотором диапазоне относительно значения 25776,26027 / 5 = 5155,252054 лет.

Этот обобщающий вывод можно записать в виде формулы:

(П : 5)∙Г = Т,

где П – приближенное значение периода прецессии;

Г – длительность года по древним и современным календарным системам в днях;

Т– семизначная дата события в виде: год, месяц, число; год, число, месяц; год, порядковый номер дня события в году; год, день события в десятичной форме.

Воспользуемся понятием об обратных величинах (раздел 2) применительно к 1/5 приблизительного значения периода прецессии в полученной формуле.

Первые 7 знаков результата могут служить обозначением даты какого-то события 7 октября 1939 года, года начала Второй мировой войны.

Днём начала этой войны принято считать 1 сентября – день нападения Германии на Польшу. Однако действительно мировой она стала 3 сентября, после того как Англия и Франция объявили войну Германии.

В десятичной форме дата 3 сентября 1939г. предстаёт в виде 1939,67397.

Так как оккультная нумерология для познания закодированной информации позволяет перестановку цифр в числе, то дробная часть полученного выше числа 1939,7693 после перестановки цифр (или в кольцевой записи) обозначает день 3 сентября.

В итоге рассуждений, обозначив величину 5:П через t, приходим к выводу, что в мифе о рождении Осириса с помощью приближенного значения периода прецессии земной оси была закодирована расчетная формула, которую, как выяснилось при проведении расчетов [2], использовал Тот для вычисления дат запланированных им и взаимосвязанных по сценарию событий 19, 20 и 21 веков н.э.:

Г / t = T, (4)

где Г – длительность года по древним и современным календарным системам в днях;

Т и t – семизначные даты событий в виде: год, месяц, число; год, число, месяц; год, порядковый номер дня события в году; год, день события в десятичной форме.

Даты Т и t событий в (4) можно выражать через соответствующие приближенные значения периода прецессии.

Уравнение (4) я назвал формулой Тота.

Логично предположить, что, если No – число созидания, то обратная величина 1/ No должна быть связана с числом разрушения.

Воспользуемся формулой Тота, чтобы определить число разрушения, дату события, связанного с разрушением.

Примем в (4), что дата t = 1881302, а длительность года Г = 365,25. До 1918г. в XIX веке (1881.3.02) в России, на родине расшифровщика, даты определялись по юлианскому календарю, по которому длительность года равнялась 365,25 дней.

Согласно григорианскому календарю, длительность года равна 365,2425 дней. Выполнив деление, получим:

365,25 / 1881302 = 1941,474575∙10-7.

Семь первых цифр правой части равенства с точностью до 5 секунд (без учета декретного времени) по московскому времени выражают момент вероломного нападения Гитлера на Советский Союз.

Формула Тота показала, что открытие “Текстов пирамид” и начало самой разрушительной из всех войн в истории человечества – взаимосвязанные события.

Не следует, однако, считать, что между этими событиями имеются какие-нибудь причинно- следственные связи.

Формула Тота почти с такой же точностью, как и в предыдущем равенстве, связывает дату убийства Александра II (1881.3.01) с днём 22 июня 1941г.

В июне 1941г. в Самарканде велись подготовительные работы для вскрытия захоронения Тамерлана, воителя и жестокого завоевателя средневековья.

Узбекские религиозные авторитеты уговаривали археологов не делать этого, ссылаясь на древние книги, в которых якобы говорится, что, если прах Тимурленга будет потревожен, то случится война.

Гроб с останками Тамерлана, несмотря на предупреждения, был открыт 22 июня. Почти тот час же после открытия гроба проводившие работы услышали по радио сообщение о начале войны.

Появление бога-шакала, указавшего путь в погребальную камеру пирамиды Унаса и открытие “Текстов пирамид” французским археологом, убийство Александра II, предупреждение аксакалов, вскрытие советскими археологами гроба Тамерлана и начало войны – эти события объединены не мистической связью, а реализующимся численно событийным сценарием Тота.

Древние мифы в закодированной различными способами форме указывают на связь периодически повторяющихся вселенских катастроф с прецессией земной оси (Г. Хэнкок).

В формуле Тота связь чисел созидания (1881302) и разрушения (1941.6.22) с 1/5 значения периода прецессии земной оси с убеждающей точностью представлена математически.

Воспользуемся формулой Тота ещё раз, приняв в ней за величину Г длительность обычного года и положив t = 1881302:

365/1881302 = 1940,145708∙10-7 ≈ 1940,14571∙10-7.

Начало (1940) и конец (7.1) приближённого значения результата – обозначения года моего рождения и дня Рождества Христа Спасителя. Середина числа (145) после кодовой замены (1-А-Аз-19) – обозначение года окончания войны, начавшейся 22 июня 1941г.

Примем триаду 708 в конце более точного значения результата за обозначение дня 7 августа (7.08).

Порядковый номер этого дня (219) после постановки точки становится обозначением Рожества Богоматери (21 сентября), а в кольцевой записи триады 219 читается порядковый номер 129 дня 9 мая. Год моего рождения кодовой заменой (0-О-16) преобразуется в 1941.6.

Конечно, к датам начала и конца отгремевшей войне я не имею прямого отношения, однако я имею самое непосредственное отношение к числу 1881302, выражающему значение впервые вычисленной мною мировой константы No и к расшифровке исходного сценария богов, в котором были запрограммированы войны, даты их начал и окончаний.

По календарю майя нынешней цивилизации отпущено на существование 5125 лет, что соответствует примерному значению 1/5 периода прецессии.

Проведенная расшифровка мифа о рождении бога созидания показывает, что его создатель рождению мифического бога созидания Осириса ставит в соответствие познание тайн строения материи, в конечном итоге выразившееся в получении “числа созидания” No [1], через которое выражаются относительные массы элементарных частиц.

Для русского уха имя бога созидания древних египтян звучит как комбинация двух слов “оси” и “рис(унок)”.

В графическом представлении формула (4) Тота (Г = Т∙t) при различных значениях Г выражается рисунком семейства гипербол на координатной плоскости ТОt.

Использование осей ОТ и Оt для обозначения временных координат является общепринятым. В соответствии с шифром Тота (раздел 2) обозначение начала координат О – Осирис.

Точки гипербол соответствуют произведению (результату умножения) времени событий, а обозначение координатной плоскости ТОt совпадает с именем Умножителя времени Тота.

Графическое представление формулы (4) шифром Тота согласовано с содержанием мифа о рождении Осириса.

Родительный падеж слова “гиперболы” по звучанию может быть переведен на русский язык, как “очень большой шар”. В свою очередь, очень большой шар (гипербол) является метафорой слов комета, болид, астероид.

Каждой точке гипербол семейства соответствуют на осях ОТ и Оt даты взаимосвязанных по сценарию Тота событий. Событием, несомненно, глобального значения будет столкновение кометы Биела с Землёй 22 декабря 2012г.

В ожидании грядущего столкновения этот високосный год покажется людям самым длинным.

Чтобы узнать дату события, связанного с датой столкновения (2012.12.22), обратимся к формуле Тота (бога Луны), приняв длительность года Г, равной наибольшей длительности года по используемым в настоящее время календарным системам.

На родине Иоанна Богослова, сказавшего, что “В начале было Слово”, в самом длинном високосном году (шаламиме) лунно-солнечного календаря 385 суток.

В разделе 3 было показано, что в логарифме числовой кальки (1913030) слова СЛОВО, означающего “Абсолютное Знание от начала начал” закодирована дата открытия кометы Биела. Подставив 385 и 20121222 в формулу Тота, получим:

385 / 20121222 = 1913,402675∙10-8.

В 1913г. Россия праздновала 300-летие царствовавшего Дома Романовых.

В разделе 3 цифровая калька СЛОВА из 1 ст. 1 гл. Евангелия Иоанна Богослова была представлена в виде 1913030.

Достаточно произвести перестановку нуля в кальке СЛОВА, чтобы получить обозначение указанного события – 1913300.

Такая возможность получения обозначения юбилейного года указывает на связь СЛОВА с датами важных событий в истории России, родины расшифровщика сценария.

21 февраля 1613г. Всероссийский собор из представителей дворян, духовенства, купцов и служилого казачества избрал на престол первого из Романовых – Михаила Федоровича.

Дата 300-летия династии Романовых может быть записана в виде 1913.21.2. или в виде 1913.21.02.

При прочтении второго варианта записи даты справа налево первые четыре знака дают обозначение года столкновения Земли с кометой Биела – 2012.

Уместно напомнить, что в логарифме числовой кальки СЛОВА справа налево читается дата открытия кометы (раздел 3), а числовой определитель (11) 1 ст. 1 гл. Евангелия Иоанна Богослова является обозначением 2012г, закодированным с помощью принципов дополнительности и эквивалентности.

По шифру Тота, используя принцип идентичности по звучанию, АБ Б можно представить в виде ab Б(ога), что означает от Бога. Эта расшифровка показывает, что и СЛОВО, и царская власть – от Бога.

В полученном выше по формуле Тота результате, после цифр 1913, означающих “Абсолютное Знание ab (от)” (см. раздел 3), следуют краткое обозначение года моего рождения 40, порядковый номер дня моего рождения в обычном году – 267 и числовой аналог буквы Д (по шифру Тота Д – день, дата).

Расшифровка полученного результата показывает, что Абсолютное Знание о будущем (знание о том, “чему надлежит быть вскоре”) люди получат от родившегося 24 сентября 1940г. (40.24.9).

Обратимся к формуле Тота еще раз, приняв в ней t = 1913,40249∙10-8:

385 / 1913, 40249∙10-8 = 20121223,95.

Семь первых знаков правой части равенства служат обозначением первого дня мира после Победы над 3-им Антихристом, первого дня новой эпохи – 23 декабря 2012г., а два знака после запятой – обозначение дня 9 мая, Дня Победы над 2-ым Антихристом. Ассоциации вселяют надежду.

Не исключено, что 22 и 23 декабря выражают один и тот же момент времени с учетом различия времени для Восточного и Западного полушарий.

В разделе 3 при раскодировании слова СЛОВО три последних буквы по идентичности звучания с латинским ovo, были расшифрованы, как яйцо – начало начал.

Имеет место и другая расшифровка этих букв. Заменив буквы ОВО их порядковыми номерами в русском алфавите, получим число 16316.

Как указывалось выше, имя бога созидания древних египтян для русского уха звучит как комбинация двух слов – оси и рис(унок).

В следующем разделе будет показано, что имя Бога Е(е), совпадающее с обозначением основания натуральных логарифмов, с древнейших времен закодировано в различных источниках.

Источник