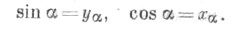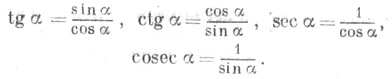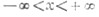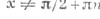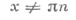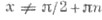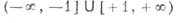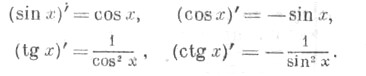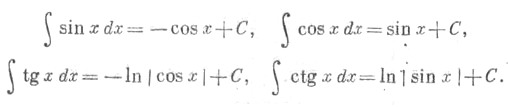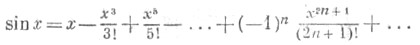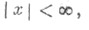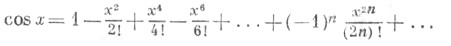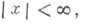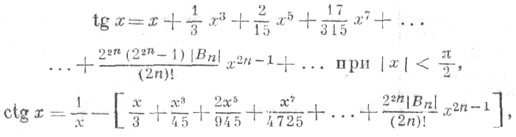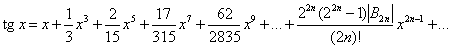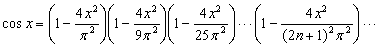что такое sec в photomatch

Что такое SEC в математике?

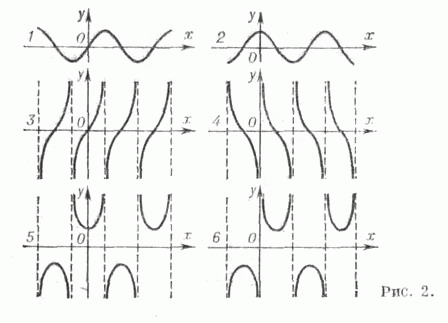
Функция SEC — это одна из математических и тригонометрических функций. Она возвращает секанс заданного угла в радианах. где x — это угол в радианах, секанс которого требуется вычислить.

Что значит SEC в тригонометрии?

Величина, обратная косинусу этого угла (числа) – называется секансом х и обозначается через sec x: … Функция у = sec x – одна из тригонометрических функций, раньше (примерно до 60-х годов прошлого века) эта функция изучалась в школьном курсе тригонометрии. Сейчас ее изучение не обязательно.

Чему равен SEC?

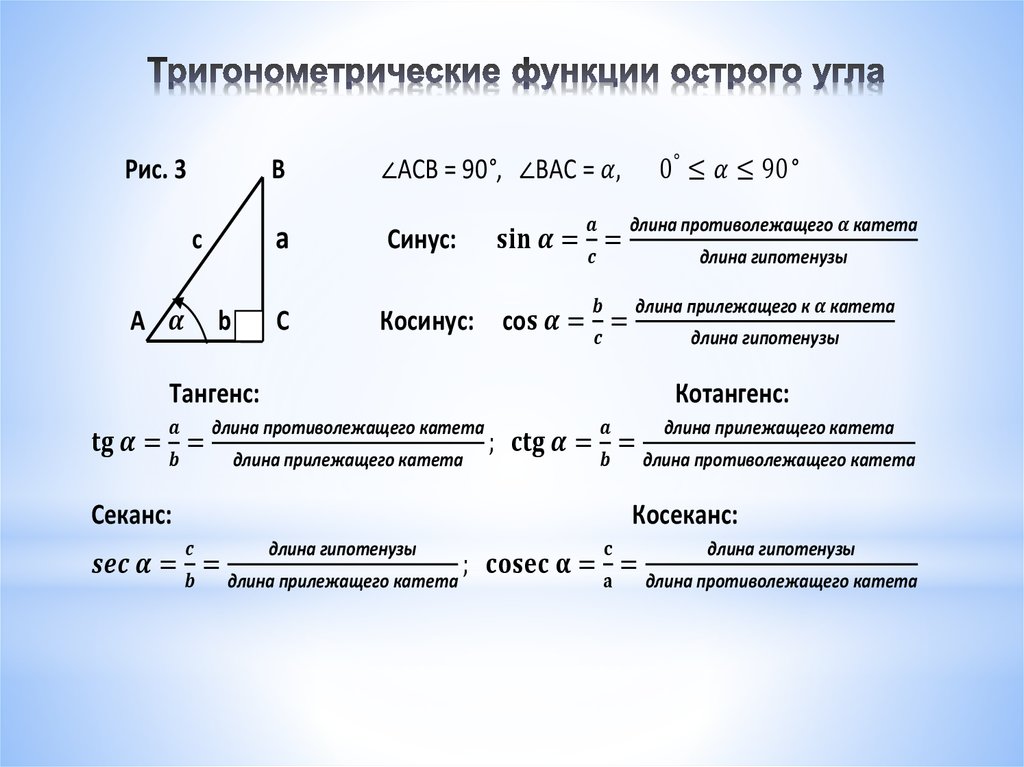
СЕКАНС, в ТРИГОНОМЕТРИИ — отношение длины гипотенузы к длине катета, прилежащего к данному острому углу в прямоугольном ТРЕУГОЛЬНИКЕ. Секанс угла А обычно сокращенно записывается, как sec А, и равен обратному КОСИНУСУ, т. е. 1/cos A.

Что такое CSC в тригонометрии?

Функция CSC — это одна из математических и тригонометрических функций. Она возвращает косеканс заданного угла в радианах. где x — это угол в радианах, косеканс которого требуется вычислить.

Что такое Секанс и Косеканс?

Косинусом угла α называется отношение прилежащего катета к гипотенузе. … Секанс угла α представляет собой отношение гипотенузы к прилежащему катету. Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.

Что такое Косеканс?

КОСЕКАНС, в ТРИГОНОМЕТРИИ — отношение длины ГИПОТЕНУЗЫ к длине стороны, противоположной острому углу в прямоугольном треугольнике. Косеканс угла А обычно сокращенно обозначают как cosec (А). Это величина, обратная синусу. Научно-технический энциклопедический словарь.

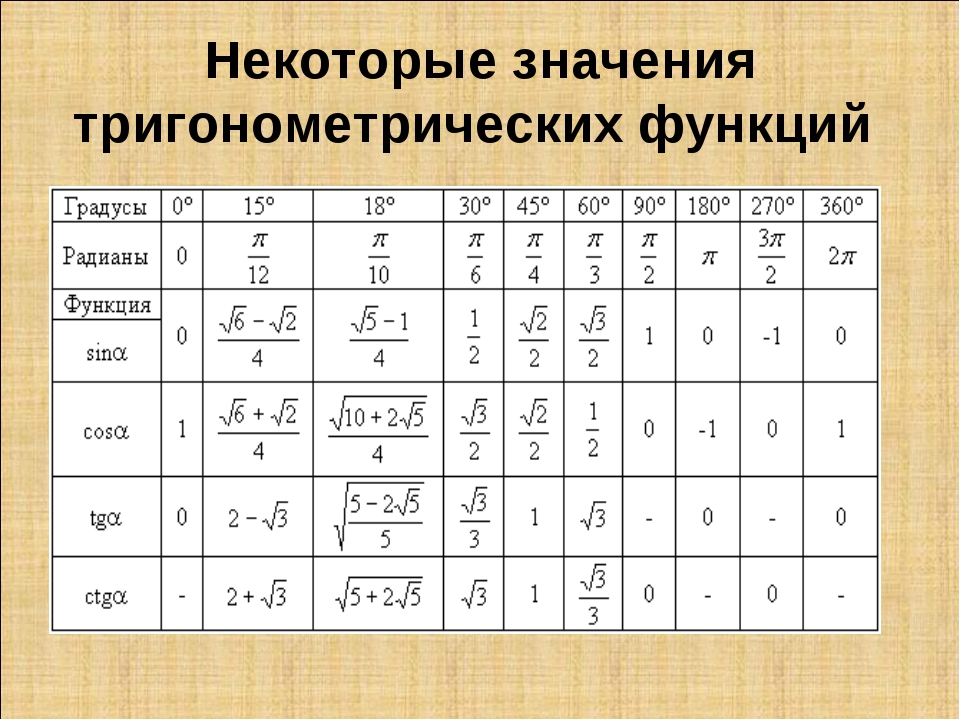
Что такое синус и косинус простыми словами?

Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике: Синус угла – отношение противолежащего катета к гипотенузе; Косинус угла – отношение прилежащего катета к гипотенузе; … Котангенс угла – отношение прилежащего катета к противолежащему.

Что называется Косинусом угла а?

Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. Определение. Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе. … Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.

Чему равен синус угла в произвольном треугольнике?

Находить синус угла в произвольном треугольнике проще всего с использованием теоремы косинусов (cos): квадрат длины любой стороны равен сумме квадратов длин двух других сторон за минусом их удвоенного произведения на косинус угла между ними.

Что такое тангенс угла?

Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе. … Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).

Где используется синус и косинус?

Синусы и косинусы часто присутствуют в формулах разных расчетов, инженерных или научных. Часто с синусами и косинусами приходится сталкиваться геодезистам. Они имеют специальные инструменты для точного измерения углов.

Что такое синус числа?

Синус некоторого числа — это значение ординаты на плоскости, которая соответствует точке этого числа на единичной окружности. Косинус некоторого числа — это значение абсциссы на плоскости, которая соответствует точке этого числа на единичной окружности.

Что такое Cosec в математике?

тригонометрические функции — функции угла: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec). … Обратные тригонометрические функции — (круговые функции, аркфункции) математические функции, являющиеся обратными к тригонометрическим функциям.

Что означает слово тригонометрия?

-греч. τρίγωνον «треугольник» и μετρέω «измеряю», то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии. Данный термин впервые появился в 1595 г.

Почему синус называется синусом?

Слово «синус» — латинского происхождения. Слово «синус» хорошо известно врачам в значении «пазуха», «впадина». … Однако ни одно из этих многочисленных значений не имеет никакого отношения к синусу в тригонометрии.

Как работает синус?

Источник

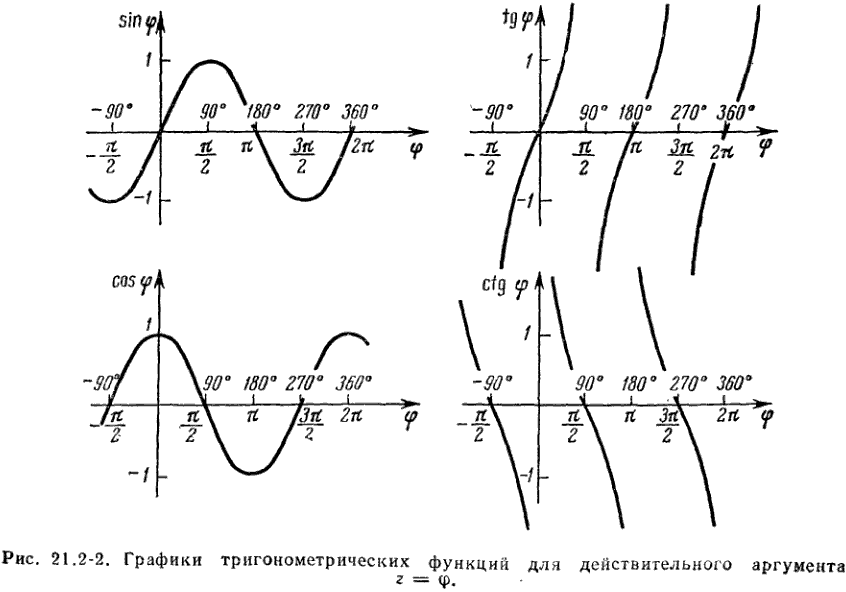
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

Если 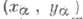— прямоугольные декартовы координаты точки А, то Т. ф. синус и косинус определяются формулами

Остальные Т. ф. могут быть определены формулами

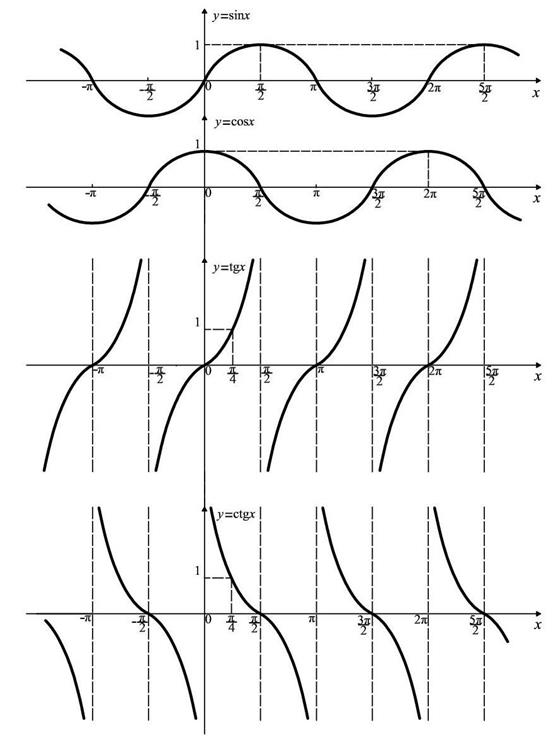
Все Т. ф.- периодические функции. Графики Т. ф. даны на рис. 2.

Основные свойства Т. ф.: область определения, множество значений, четность и участки монотонности приведены в табл.

Каждая Т. ф. в каждой точке своей ооласти определения непрерывна и бесконечно дифференцируема; производные Т. ф.:

Все Т. ф. допускают разложение в степенные ряды:

при

при

Полезное

Смотреть что такое «ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ» в других словарях:

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — (от греческого trigonon треугольник и функция), функции угла. Таковы, например, синус (sin a), косинус (cos a), тангенс (tg a), котангенс (ctg a). Они выражают отношения длин сторон прямоугольного треугольника. Например, sin a отношение длины… … Современная энциклопедия

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — функции угла: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec). Их можно определить как отношения длины r и проекций а и b на оси координат радиуса вектора, образующего с положительным направлением оси Ох… … Большой Энциклопедический словарь

Тригонометрические функции — (от греческого trigonon треугольник и функция), функции угла. Таковы, например, синус (sin a), косинус (cos a), тангенс (tg a), котангенс (ctg a). Они выражают отношения длин сторон прямоугольного треугольника. Например, sin a отношение длины… … Иллюстрированный энциклопедический словарь

Тригонометрические функции — Запрос «sin» перенаправляется сюда; см. также другие значения. Запрос «sec» перенаправляется сюда; см. также другие значения. Запрос «Синус» перенаправляется сюда; см. также другие значения … Википедия

Тригонометрические функции — один из важнейших классов элементарных функций. Для определения Т. ф. обычно рассматривают окружность единичного радиуса с двумя взаимно перпендикулярными диаметрами A A и B B (рис. 1). От точки А по окружности откладываются дуги … Большая советская энциклопедия

тригонометрические функции — функции угла: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec). Их можно определить как отношения длины r и проекций а и b на оси координат радиуса вектора, образующего с положительным направлением оси Ох… … Энциклопедический словарь

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — ф ции угла: синус (sin), косинус (cos), тангенс (tg), котангенс> (ctg), секанс (sес), косеканс(соsес). Т. ф. можно определить как отношения длины г и проекций а и b на оси координат радиус вектора, образующего с положит. направлением оси Ох угол… … Большой энциклопедический политехнический словарь

Обратные тригонометрические функции — (круговые функции, аркфункции) математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций: арксинус (обозначение: arcsin) арккосинус (обозначение: arccos)… … Википедия

Обратные тригонометрические функции — аркфункции, круговые функции, решают следующую задачу: найти дугу (число) по заданному значению её тригонометрической функции. Шести основным тригонометрическим функциям соответствуют шесть О. т. ф.: 1) Arc sin х («арксинус x») функция,… … Большая советская энциклопедия

Редко используемые тригонометрические функции — Редко используемые тригонометрические функции функции угла, которые в настоящее время используются редко по сравнению с шестью основными тригонометрическими функциями (синусом, косинусом, тангенсом, котангенсом, секансом и косекансом). К… … Википедия

Источник

Тригонометрические функции

Формулы понижения степени.

Из формул кратного аргумента выводятся формулы:

С помощью этих формул тригонометрические уравнения можно приводить к уравнениям более низких степеней. Таким же образом можно вывести и формулы понижения для более высоких степеней синуса и косинуса.

Каждая тригонометрическая функция в каждой точке своей области определения непрерывна и бесконечно дифференцируема. Причем и производные тригонометрических функций являются тригонометрическими функциями, а при интегрировании получаются так же тригонометрические функции или их логарифмы. Интегралы от рациональных комбинаций тригонометрических функций всегда являются элементарными функциями.

Формулы приведения.

– a+ a p – a p + a+ a+ a2 p – asin bcos acos asin a–sin a–cos a–cos a–sin acos bsin a–sin a–cos a–cos a–sin asin acos a

1) название функции сохраняется, если k четное, и меняется на «дополнительное», если k нечетное;

Четность и периодичность.

Функция называется четной, если f(–x) = f(x). Функции косинус и секанс – четные, а синус, тангенс, котангенс и косеканс – функции нечетные:

Периодичность синуса и косинуса следует из того, что все точки P _{a + 2k p} , где k = 0, ±1, ±2,…, совпадают, а периодичность тангенса и котангенса – из того, что точки P _{a + k p} поочередно попадают в две диаметрально противоположные точки окружности, дающие одну и ту же точку на оси тангенсов.

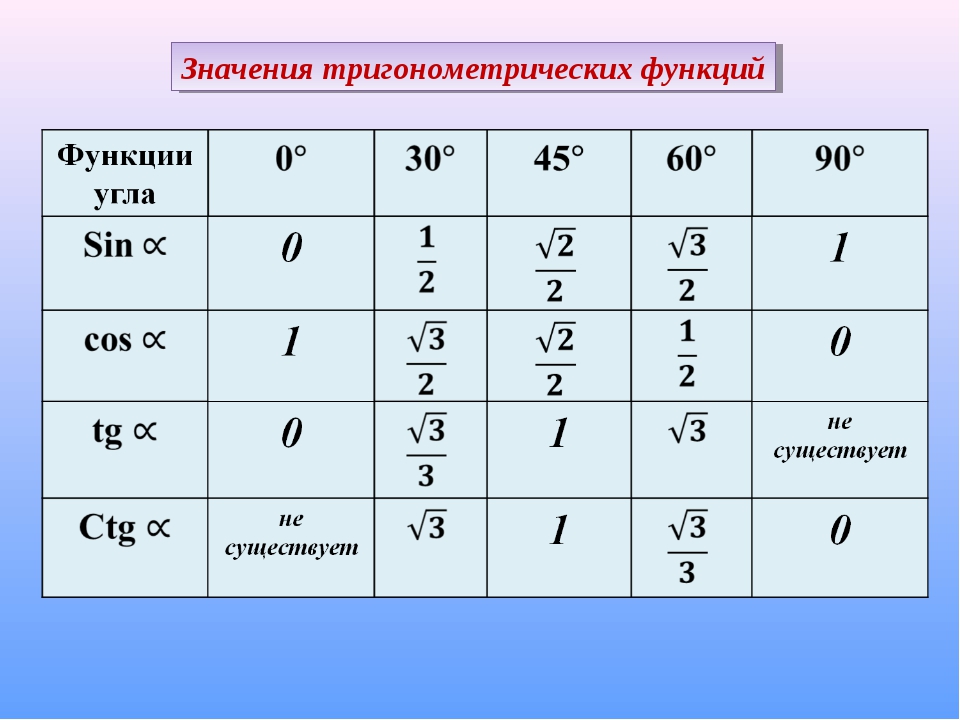
Основные свойства тригонометрических функций могут быть сведены в таблицу:

Тригонометрические функции комплексного аргумента

определяются как аналитические продолжения соответствующих тригонометрических функций действительного аргумента в комплексную плоскость. Так, sin z и cos z могут быть определены с помощью рядов для sin x и cos x,если вместо x поставить z:

Эти ряды сходятся по всей плоскости, поэтому sin z и cos z – целые функции.

Тангенс и котангенс определяются формулами:

Функции tg z и ctg z – мероморфные функции. Полюсы tg z и sec z – простые (1-го порядка) и находятся в точках z = p /2 + p n, полюсы ctg z и cosec z – также простые и находятся в точках z = p n, n = 0, ±1, ±2,…

Все формулы, справедливые для тригонометрических функций действительного аргумента, справедливы и для комплексного. В частности,

т.е. четность и нечетность сохраняются. Сохраняются и формулы

т.е. периодичность также сохраняется, причем периоды такие же, как и для функций действительного аргумента.

Тригонометрические функции могут быть выражены через показательную функцию от чисто мнимого аргумента:

Обратно, eiz выражается через cos z и sin z по формуле:

Эти формулы носят название формул Эйлера. Леонард Эйлер вывел их в 1743.

Тригонометрические функции также можно выразить через гиперболические функции:

z = –i sh iz, cos z = ch iz, z = –i th iz.

где sh, ch и th – гиперболические синус, косинус и тангенс.

Тригонометрические функции комплексного аргумента z = x + iy, где x и y – действительные числа, можно выразить через тригонометрические и гиперболические функции действительных аргументов, например:

Синус и косинус комплексного аргумента могут принимать действительные значения, превосходящие 1 по абсолютной величине. Например:

Если неизвестный угол входит в уравнение как аргумент тригонометрических функций, то уравнение называется тригонометрическим.Такие уравнения настолько часто встречаются, что методы ихрешения очень подробно и тщательно разработаны. С помощью различных приемов и формул тригонометрические уравнения сводят к уравнениям вида f(x) = a, где f – какая-либо из простейших тригонометрических функций: синус, косинус, тангенс или котангенс. Затем выражают аргумент x этой функции через ее известное значение а.

Поскольку тригонометрические функции периодичны, одному и тому же а из области значений отвечает бесконечно много значений аргумента, и решения уравнения нельзя записать в виде одной функции от а.Поэтому в области определения каждой из основных тригонометрических функций выделяют участок, на котором она принимает все свои значения, причем каждое только один раз, и находят функцию, обратную ей на этом участке. Такие функции обозначают, приписывая приставку агс (дуга) к названию исходной функции, и называют обратными тригонометрическимифункциями или просто аркфункциями.

Представление тригонометрических функций в виде степенных рядов и бесконечных произведений.

Все тригонометрические функции допускают разложение в степенные ряды. При этом функции sin x b cos x представляются рядами. сходящимися для всех значений x:

Эти ряды можно использовать для получения приближенных выражений sin x и cos x при малых значениях x:

Функции sin x и cos x могут быть представлены в виде бесконечных произведений:

(эта формула была получена Эйлером в 1740);

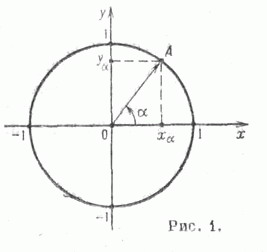
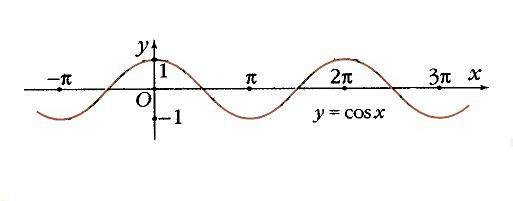
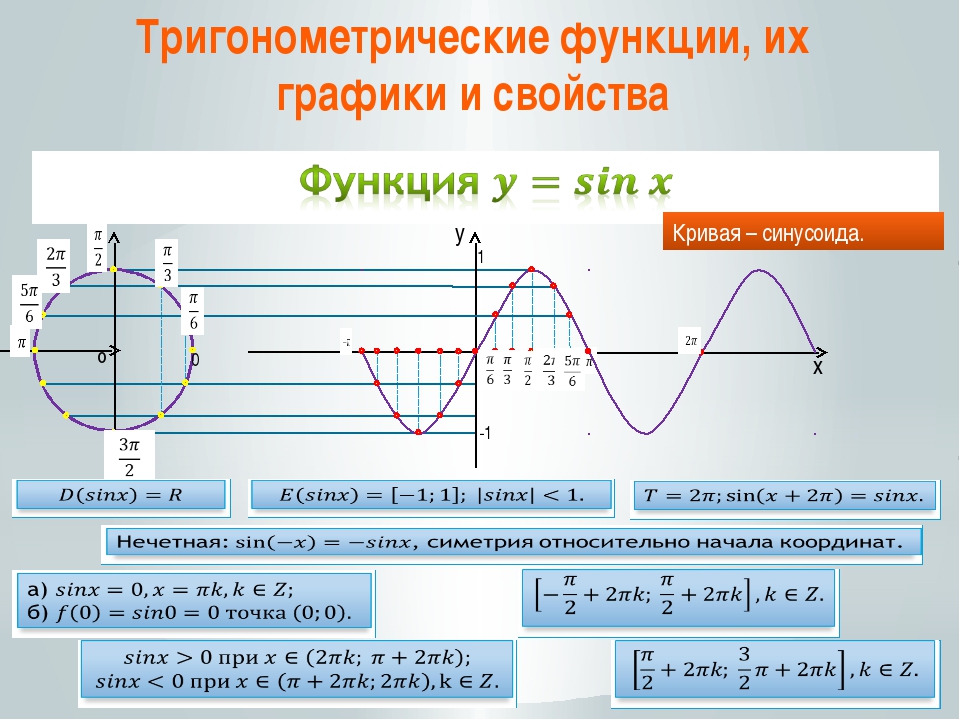
Функция у = cos х.

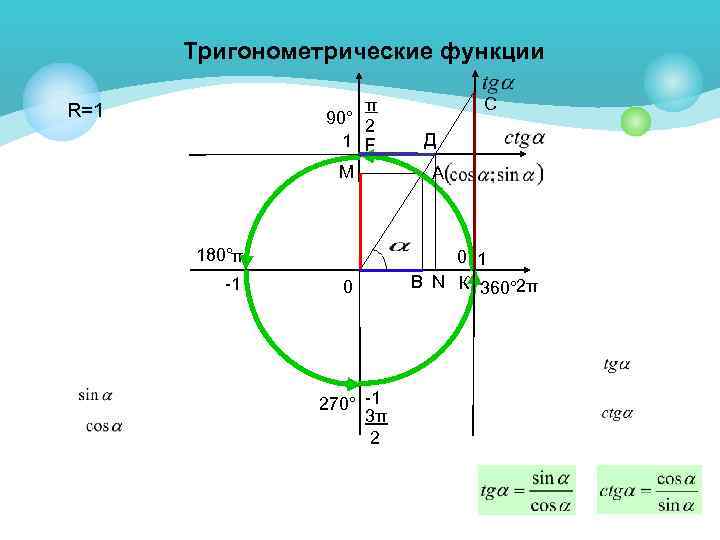
Если построить единичную окружность с центром в начале координат, и задать произвольное значение аргумента xи отсчитать от оси Ox угол x_0,то этому углу на единичной окружности соответствует некоторая точка A (рис. 1)а ее проекцией на ось Ох будет точка М.Длина отрезка ОМ равна абсолютной величине абсциссы точки A. Данному значению аргумента xсопоставлено значение функции y =cos xкак абсциссы точки А.Соответственно точка В (x; у)принадлежит графику функции у = cos х (рис. 2).Если точка А находится правее оси Оу,токосинус будет положителен, если же левее – отрицателен. Но в любом случае точка А не может покинуть окружность. Поэтому косинус лежит в пределах от –1 до 1:

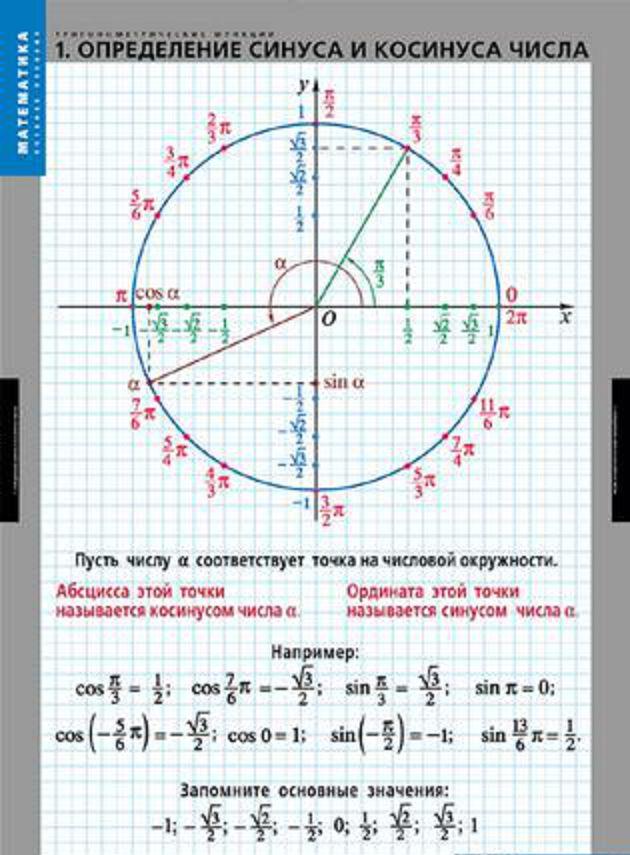
Если взять два значения аргумента, равные по абсолютной величине, но противоположные по знаку, x и –x,найти на окружности соответствующие точки A_x и А_-x.Как видно на рис. 3их проекцией на ось Ох является одна и та же точка М.Поэтому

Значит, можно исследовать свойства функции y = cos х на отрезке [0, p ], а затем учесть ее четность и периодичность.

Источник

Что такое SEC. Объясняем простыми словами

В сфере интересов SEC находятся все операции с ценными бумагами в США. Основная задача регулятора — обеспечить прозрачность сделок и противодействовать мошенническим схемам, чтобы сохранить доверие инвесторов к фондовому рынку.

Для этого SEC устанавливает правила регистрации ценных бумаг и отслеживает их выполнение. Комиссия также следит за обращением акций и облигаций, деятельностью брокеров, торговыми операциями частных инвесторов и инвесткомпаний, появлением пузырей, манипуляциями и т. д.

Комиссия по ценным бумагам и биржам США также занимается расследованиями нарушений. Разбирательство может быть инициировано, если произошла кража ценных бумаг, вскрылись договорные сделки или факты использования инсайдерской информации и т. д.

SEC обладает неоспоримым авторитетом в экономической сфере, а также независимой судебной системой, благодаря которой участвует в самых сложных юридических спорах на рынке. Инструменты и методы, которые используются регулятором для разрешения различных процессов и конфликтных ситуаций, стали своего рода эталоном и примером для международных регуляторов.

Пример употребления на «Секрете»

(Из новости о вознаграждениях, которые американский регулятор выплачивает осведомителям.)

Нюансы

Под контроль Комиссии по ценным бумагам и биржам США подпадают любые компании (в том числе и российские), акции которых торгуются на американских биржах. Основанием для расследования со стороны SEC могут стать любые нарушения законодательства в сфере оборота ценных бумаг и обслуживания инвесторов. В числе таких обстоятельств значится также и отказ от предоставления финансовой информации контролирующим органам.

Особенно большое внимание SEC обращает на сделки, имеющие признаки корпоративного поглощения. Например, если инвестор приобретает пакет в 5% и более от числа акций компании, это событие обязательно становится предметом пристального внимания со стороны SEC. В связи с этим рейдерские захваты предприятий оказываются практически невозможными.

Кроме того, интерес SEC могут вызвать жалобы клиентов на недобросовестное брокерское обслуживание, подозрение на использование инсайдерской информации, манипулирование ценами и пр.

Регулятор обеспечивает информационную поддержку инвесторов и трейдеров. Законы и правила, регулирующие американскую индустрию ценных бумаг, основываются на идее о том, что все инвесторы — от частных лиц до крупных институтов — должны иметь доступ к полной, точной и актуальной информации о том или ином активе либо компании. Это позволяет участникам рынка быть в курсе происходящих событий и принимать наиболее эффективные инвестиционные решения.

Информация, которую компании должны предоставлять в SEC:

Практика

Ежегодно SEC рассматривает множество правонарушений. Наиболее частыми из них оказываются:

неправомерные действия брокеров в отношении клиентов.

При выявлении подобных нарушений SEC вправе определять размеры штрафов, изымать нелегально полученную прибыль, запрещать частным лицам и компаниям проводить операции с ценными бумагами и налагать запрет на незаконные действия.

Если же заходит речь о необходимости уголовного преследования, регулятор объединяет усилия с министерством юстиции США, Федеральным бюро расследований (ФБР) или прокуратурами штатов.

Один из самых резонансных за последние годы скандалов на фондовом рынке США связан с заявлением миллиардера Илона Маска о намерении скупить все акции компании Tesla, которую он же и возглавлял. Анонс вызвал переполох на биржах, взвинтив стоимость ценных бумаг производителя электромобилей. Проведённое SEC расследование показало, что Маск не располагал необходимыми средствами, не говоря уже о реальном намерении совершить сделку.

История SEC ведётся с 1934 года. Тогда США переживали последствия Великой депрессии, на биржах орудовали мошенники, а рядовые инвесторы перестали доверять государственным структурам. Это и стало толчком к созданию организации, получившей фактически чрезвычайные полномочия. Первым руководителем SEC стал Джозеф Кеннеди, отец будущего президента США Джона Кеннеди.

Источник