что такое сар в автоматизации

Что такое сар в автоматизации

13. Системы автоматического регулирования

Системы автоматического регулирования (САР) применяются для регулирования отдельных параметров (температура, давление, уровень, расход и т.д.) в объекте управления. В современных системах автоматического управления (САУ) системы автоматического регулирования являются подсистемами САУ и их применяют для регулирования различных параметров при управлении объектом или процессом.

Принцип действия всякой системы автоматического регулирования (САР) заключается в том, чтобы обнаруживать отклонения регулируемых величин, характеризующих работу объекта или протекание процесса от требуемого режима и при этом воздействовать на объект или процесс так, чтобы устранять эти отклонения.

Для осуществления автоматического регулирования к регулируемому объекту подключается автоматический регулятор, вырабатывающий управляющее воздействие на регулирующий орган. Это управляющее воздействие вырабатывается регулятором в зависимости от разности между текущим значением регулируемой величины (температуры, давления, уровня жидкости и т. д.), измеряемой датчиком, и желаемым её значением, устанавливаемым задатчиком. Регулируемый объект и автоматический регулятор вместе образуют систему автоматического регулирования.

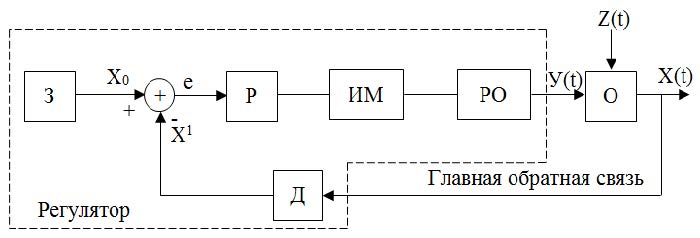
Основным признаком САР, является наличие главной обратной связи, по которой регулятор контролирует значение регулируемого параметра.

Пример системы регулирования температуры

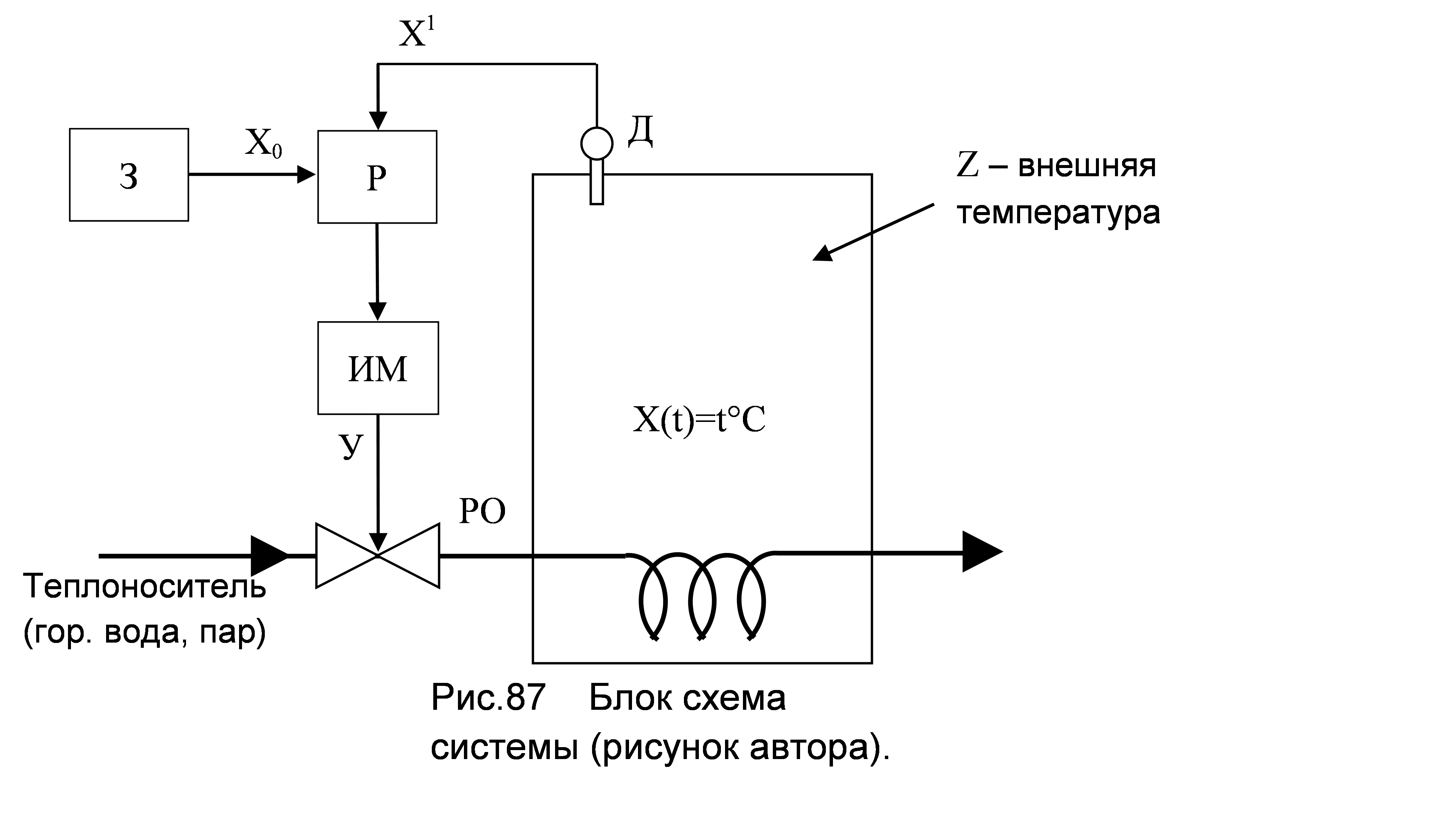
На Рис. 87 показана блок схема системы регулирования температуры в объекте, а на Рис. 88 функциональная схема САР, показывающая общий принцип работы любой системы автоматического регулирования.

Рис. 88 Функциональная схема САР

З – задатчик, для установки заданного значения параметра X₀

Д – датчик (термопара, терморезистор, датчик уровня, скорости и др. для разных систем)

ИМ – исполнительный механизм (эл. мотор с редуктором, пневмоцилиндры и др.)

РО – регулирующий орган (кран, вентиль, заслонка и др.)

О – объект регулирования (печь, эл. мотор, резервуар и др.)

У – регулирующее (управляющее) воздействие

Z – помеха (возмущение)

Х – регулируемый параметр

X 1 – сигнал на выходе датчика

X₀ – заданное значение регулируемого (управляемого) параметра может быть постоянным X₀ или изменяемым (Ut).

Сигнал с задатчика может быть:

-может изменяться во времени U(t) по определённой программе (программное регулирование);

-может изменяться во времени U(t) в соответствии с измеряемым внешним процессом (следящее регулирование).

1.От каких воздействий может измениться регулируемый параметр?

2.Как действует обратная связь, и для чего она нужна?

3.Какие функции выполняют Д и ИМ?

4.Как действует система при возникновении ошибки «е»?

5.Приведите пример системы стабилизации и следящей системы?

Источник

Что такое система автоматического регулирования?

При современном развитии техники системы автоматического регулирования (САР) встречаются практически повсюду, как на высокотехнологических производствах, так и в бытовых приборах (стиральная машина, стабилизаторы напряжения). Такие системы очень активно внедряются, благодаря удобству при их использовании, а также исключая человеческий фактор при управлении различными процессами.

Для осуществления автоматического управления применяют довольно сложные устройства, именуемые автоматическими регуляторами. Эти устройства должны формировать управляющие воздействия на объект регулирования на основании измерения переменных подлежащих регулированию. Такое управления может осуществляться по принципу замкнутого и разомкнутого цикла.

Разомкнутый принцип управления

В таких системах не используют обратные связи и по своей структуре они довольно просты. Пример схемы такой системы показан ниже:

Это система управления скоростью вращения якоря двигателя постоянного тока которая имеет следующий алгоритм работы: задающее воздействие перемещает движок 2 потенциометра 1, тем самым меняя напряжение на усилителе 3. Изменение напряжения приводит к изменению тока машины 4 и соответственно его скорости вращения. Измерение скорости вращения машины измеряют с помощью тахогенератора 5 и с помощью стрелочного прибора 6 приводят напряжение на выходе тахогенератора к доступному для человеческого глаза виду. Если движок потенциометра будет приводить в движение человек, то такое управление называют ручным.

В данной схеме отсутствует обратная связь, поэтому ее называют разомкнутой. Регулирование координат таким образом довольно проблематичное занятие, так как чтоб получить точное значение скорости необходимо провести довольно точную градуировку системы, что довольно таки затруднительно. Даже при отличной градуировке все элементы системы подвержены износу, что делает необходимым производить частые градуировки. Также при изменении какого – то параметра (например, возрос момент нагрузки вала) скорость вращения электродвигателя просядет, но система никак не отреагирует на это. Поэтому, если нужно поддреживать какую – то из переменных величин постоянной, используют замкнутые системы управления.

Замкнутый принцип управления

Такая система отличается от предыдущей лишь наличием обратной связи по скорости. Схема ниже:

Наличие обратной связи с тахогенератора 5 сравнивать заданную скорость вращения с реальной и в итоге возникает ошибка ∆U = U_П – U_ТГ. При этом сигнал ошибки будет подаваться на усилитель, который в свою очередь будет увеличивать скорость якоря машины до тех пор, пока ошибка ∆U не станет равной нулю или значению допустимой ошибки. Допустимая ошибка в таких системах определяется необходимой точностью, задаваемой технологическим процессом.

При автоматическом регулировании могут сочетать оба принципа управления и замкнутый и разомкнутый в сочетании друг с другом.

Возмущающие и задающие воздействия

Системы автоматического управления характеризуют по возмущающим и управляющим воздействиям.

Воздействие, стремящееся нарушить функциональную связь между регулируемой переменной и задающим воздействием, называют возмущающим. Для систем показанных выше таким воздействие может быть момент нагрузки, ток возбуждения электродвигателя.

Применительно системы выше напряжение на потенциометре будет задающим воздействием.

Также стоит отметить, что задающее воздействие g(t) может приложено только к элементу сравнения, то возмущающее – к любой точке системы.

Такие воздействия приводят к тому, что требуемые и реальные величины регулирования могут отличатся друг от друга. Разность между такими воздействиями называют ошибкой системы регулирования.

Разность между регулируемой величиной в данный промежуток времени и некоторым ее постоянным значением, принятым за номинальное, именуют отклонением величины регулируемой. (рис. а)).

При постоянном возрастании управляющего воздействия, ошибка регулирования ε(t) будет оставаться постоянной величиной, как показано ниже (рис. б)):

Где: g(t) – воздействие управляющее;

х(t) – величина регулируемая (на выходе системы);

f(t) – воздействие возмущающее;

Системы с обратной связью

САР имеющая одну регулируемую величину показана ниже:

Введение в данном случае обратной связи заставляет устройство реагировать на изменение возмущения f(t), что делает из устройства некий фильтр, который довольно точно передает управляющее воздействие и подавляет возмущающее. Сигнал, поступающий из выхода на вход, именуют сигналом обратной связи, а разницу между сигналом задания и обратной связью называют ошибкой.

Ошибка, возникающая в каждом элементе устройства, оказывает влияние на вход следующего элемента, тем самым наращивая сигнал ошибки.

Итак, можем сделать вывод что САР – это динамическая система, которая стремится сохранить в допустимых пределах отклонение между заданным и реальным значением регулируемой величины, используя при этом метод сравнения сигналов обратной связи получаемых с выхода устройства, с сигналами, поступающими на вход устройства.

Источник

Классификация и основные устройства САР

Управляющее воздействие системы g(t) может изменятся по различным законам. Поэтому в зависимости от таких изменений САР подразделяют на основные классы, а именно: следящие системы, автоматической стабилизации (регулирования) и программного управления.

Автоматическое регулирование

Давайте рассмотрим на примере схеме показанной ниже:

Если предположить что в данной САР движок 2 потенциометра 1 неподвижен, то есть задающий сигнал не изменяющийся во времени, то такая система будет называться системой автоматического регулирования скорости вращения вала электромашины. Ее задача поддерживать постоянство скорости машины. Имеющий постоянное значение входной сигнал будет носить название уставки или настройки регулятора. Он зависит от требований к стабилизируемой величине.

Программное регулирование

Если этот же движок 2 потенциометра 1 будет перемещаться по какому-то алгоритму или программе, например с помощью кулачкового механизма, а снимаемое на выходе потенциометра напряжение изменяется по определенному закону, то такой способ управления будет носить название программного управления.

Следящая система

А вот если движок 2 потенциометра 1 будет перемещаться по неизвестному закону, скажем в зависимости от показаний какого – то прибора, а угловая скорость машины находится в зависимости от положения движка, то такая система имеет название следящей системы.

Типовая функциональная схема САР

Ниже показана функциональная схема САР с одной регулируемой переменной х(t):

Такая система состоит из автоматического регулятора и объекта, подлежащего регулированию. Объектом регулирования называет устройство, для которого нужно поддерживать заданный режим работы при помощи автоматических регуляторов. Элементы и устройства такой системы можно классифицировать следующим образом:

Задающее устройство

Оно изображено на схеме 1 и предназначено для преобразования входного сигнала g(t) с нужной пропорциональностью, а также в удобную для сравнения величину со значением регулируемой координаты х(t). Задающими устройствами могут быть резисторы, калиброванные, кулачковые контроллеры и прочие механизмы. Но при современном развитии технологий, задающими механизмами выступают, как правило, микропроцессорные устройства, которые реализуют заложенные в них алгоритмы управления.

Сравнивающее устройство

Показано 2 на схеме и служит для сравнения сигналов поступающих на вход с сигналами обратной связи. В результате таких сравнений генерирует сигнал ошибки ε(t). Зачастую представляют собой арифметическое устройство, которое суммирует или вычитает (в зависимости от типа обратных связей) сигналы поступающие на его вход из задающего элемента и элемента обратной связи.

Преобразующее устройство

На рисунке показано 3. Оно выполняет преобразования результатов полученных в ходе сравнения в форму, которая используется в процессе регулирования, при этом не выполняя ни корректирующих, измерительных или усилительных функций.

Корректирующие устройства

Показаны как 4 и 8. Их основная задача – повышение устойчивости и улучшение динамических свойств системы автоматического управления. Корректирующие элементы бывают последовательные и параллельные. Мы не будем подробно рассматривать их в этой статье. С помощью последовательного корректирующего элемента 4 сигнал ошибки преобразуется и в закон регулирования вводят воздействия по интегралам и производным регулируемой величины по времени. При параллельном 8 – сигнал с выхода подают на вход предыдущего элемента.

Вспомогательный сравнивающий элемент

Показан цифрой 5 и предназначен для сопоставления сигналов промежуточной цепи с местной обратной связью этой же цепи.

Усилительное устройство

Цифра 6 на схеме. Оно предназначается для управления посторонними источниками энергии. Например управлением коммутацией транзисторов в инверторе напряжения, или открытием задвижек в мощных насосных станциях.

Исполнительное устройство

Показано цифрой 7 и предназначено для непосредственного r(t) воздействия на исполнительный механизм. Например, электропривод приводящий в движение валок прокатного стана.

Чувствительные или измерительные элементы

Показаны 9 и они нужны для формирования сигналов обратных связей с регулируемых величин, для дальнейшего сравнения с задающими величинами и осуществления автоматического управления. Например, таким устройством может служить тахогенератор, который преобразует скорость вращения валка прокатного стана в электрический сигнал напряжения, который дальше используется для формирования задающих сигналов.

Элемент главной обратной связи

Показан цифрой 10. Он необходим для согласования величин вырабатываемых датчиком обратной связи с величиной управляющего воздействия. Как пример, можно привести делитель напряжения тахогенератора, который преобразует напряжение выхода тахогенератора к напряжению на входе, а это порядка 0 — 15 или 0 — 24 В.

Обычно часть регулятора, которая преобразует сигнал ошибки ε(t) в воздействие регулирующее r(t) – именуют сервомеханизмом.

Таким образом можно выделить три основные части САР – объект регулирования, датчики, сервомеханизм. Такая система показана ниже:

Не стоит забывать, что на рисунках выше приведены типичные схемы САР. На практике таких схем довольно много и они могут довольно сильно между собой различаться. Также могут в управлении применять элементы, которые в себе могут хранить довольно большой функционал и выполнять роль нескольких датчиков или задающих механизмов сразу.

Источник

2. Математическое описание систем автоматического управления

Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях

При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.

На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).

При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.

Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др

Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).

где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.

В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.

Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:

где, m — масса тела, F_j — все силы воздействующие на тело (поршень демпфера)

Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:

где — сила тяжести; — сила сопротивления пружины, — сила вязконо трения (пропорциональна скорости поршеня)

Размерности сил и коэффициентов, входящих в уравнение (2.1.2):

Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть

перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:

если , то уравнение принимает вид:

Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).

Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:

тогда, разделив на k, имеем:

Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!

«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:

Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [].
Тогда уравнение (2.1.6) можно записать в операторной форме:

, что эквивалентно

где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную .

Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.

Введем новые нормированные (безразмерные) переменные:

Подставляя эти соотношения в уравнение (2.1.2), имеем:

Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на , получаем:

где: — коэффициент усиления, причем безразмерный.

Проверим размерность коэффициента

Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.

На рис. 2.1.4 представлены статические характеристики для механического демпфера:

Процедура нормировки отклонений позволяет привести уравнения динамики к виду:

где дифференциальные операторы.

Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).

А если – нелинейные дифференциальные операторы, или , то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).

Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»

2.2. Линеаризация уравнений динамики САУ (САР)

Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:

Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).

Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N₀ Рис. 2.2.1 – Пример изменения мощности реактора

Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:

Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:

Перенесем в левую часть уравнения и запишем уравнение в виде%

где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.

Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:

Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .

Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки будет выглядеть так:

C учетом вышеприведенного разложение принимает вид:

Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку , получаем:

Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:

Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.

В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:

где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора выше порядка оператора :

Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.

Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).

Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:

Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>

Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на , то уравнение принимает вид:

или в операторном виде:

Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.

Пример

Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x₀, y₀), если полное уравнение динамики имеет вид:

Нелинейность полного уравнения динамики проявляется в следующем:

• во-первых, в нелинейности статической характеристики:

• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.

Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x₀, y₀) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.

Преобразования выполним в следующей последовательности:

Перейдем к новым безразмерным переменным:

Заметим, что:
.

Подставляя значения x(t) и y(t) в исходное уравнение:

Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости: , получаем следующее уравнение:

Вводим новые обозначения:

Получаем уравнения в «почти» классическом виде:

Если в правой части вынести за общую скобку и разделить все уравнение на , то уравнение (линеаризованное) принимает вид:

Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).

2.3. Классический способ решения уравнений динамики

Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.

Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:

Переходя к полной символике, имеем:

Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.

Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).

Требуется найти y(t) при известных начальных условиях.

Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).

Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием , поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:

Напомним этапы решения:

1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:

2) Записываем характеристическое уравнение:

3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:

если среди нет повторяющихся корней (кратность корней равна 1).

Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:

Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:

5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…

Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .

6) Суммируя полученные составляющие (собственную и вынужденную), имеем:

7) Используя начальные условия (t = 0), находим значения постоянных интегрирования . Обычно получается система алгебраических уравнений. Решая систему, находим значения постоянных интегрирования

Пример

Найти аналитическое выражение переходного процесса на выходе звена, если

Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем: тогда:

где — неизвестные (пока) постоянные интегрирования.

По виду временной функции в правой части запишем как:

Подставляя в исходное уравнение, имеем:

Суммируя , имеем:

Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:

Решая систему уравнений относительно и , имеем:
Тогда окончательно:

Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:

Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).

Рис. 2.3.1 – структурная схема для проверки решения

На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).

Источник