что такое рекуррентное соотношение

Производящие функции — туда и обратно

«Производящая функция является устройством, отчасти напоминающим мешок. Вместо того чтобы нести отдельно много предметов, что могло бы оказаться затруднительным, мы собираем их вместе, и тогда нам нужно нести лишь один предмет — мешок».
Д. Пойа

Введение

Математика делится на два мира — дискретный и непрерывный. В реальном мире есть место и для того и для другого, и часто к изучению одного явления можно подойти с разных сторон. В этой статье мы рассмотрим метод решения задач с помощью производящих функций — мостика ведущего из дискретного мира в непрерывный, и наоборот.

Идея производящих функций достаточно проста: сопоставим некоторой последовательности — дискретному объекту, степенной ряд g₀ + g₁z + g₂z 2 +… + g_nz n +… — объект непрерывный, тем самым мы подключаем к решению задачи целый арсенал средств математического анализа. Обычно говорят, последовательность генерируется, порождается производящей функцией. Важно понимать, что это символьная конструкция, то есть вместо символа z может быть любой объект, для которого определены операции сложения и умножения.

История возникновения производящих функций

Известно, что начало методу производящих функций положил английский математик Абрахам де Муавр, а дальнейшему развитию и продолжению данного метода мы обязаны великому математику, имя которого Леонард Эйлер.

Метод производящих функций

Изучение этого мощного механизма позволяющего решать многие задачи, мы начнём с простенькой задачи: сколькими способами можно расположить в линию чёрные и белые шары, общее количество которых равно n?

Обозначим белый шар символом ○, чёрный — ●, T_n — искомое количество расположений шаров. Символом Ø — обозначим нулевое количество шаров. Как и любое решение комбинаторной задачи начнём с тривиальных случаев:

Если n=1, то очевидно имеется 2 способа — взять либо белый шар ○, либо взять чёрный шар ●, таким образом, T₂ = 2.

Если n=2, то имеется 4 способа расположений: ○○, ○●, ●○, ●●.

Рассмотрим случай для n=3. Мы можем начать белым шаром и продолжить 4-мя комбинациями, описанными выше ○○○, ○○●, ○●○, ○●●, или же мы можем начать чёрным шаром и аналогично продолжить 4-мя шарами ●○○, ●○●, ●●○, ●●●.

В итоге количество шаров удвоилось, то есть T₃ = 2T₂. Аналогично T₄ = 2T₃, то есть, обобщая для всех n, получаем рекуррентное уравнение T_n = 2T_n-1 которое и является решением для данной задачи. Решение такого уравнения можно легко угадать — T_n = 2 n (так как 2⋅2 n-1 = 2 n ).

А что если у нас плохо с угадыванием? И что делать, если уравнение будет сложнее? А вообще причём здесь производящие функции?

«Просуммируем» все возможные комбинации расположений шаров:

Вопрос о допустимости такой нелепой на первый взгляд суммы опустим. Будем складывать и умножать последовательности шаров. Со сложением всё понятно, но что значит умножить одну последовательность шаров на другую? Перемножив ○● на ●○ мы получим не что иное как ○●●○. Заметим, однако, что произведение шаров в отличие от произведения чисел не является коммутативным, так как ○●⋅●○ ≠ ●○⋅○●. Символ Ø — в произведении играет роль мультипликативной единицы, то есть Ø ⋅ ○○● = ○○● ⋅ Ø = ○○● и коммутирует с любой последовательностью шаров.

Производя с рядом G последовательность манипуляций, а именно вынося за скобки левый белый и чёрный шары

получим уравнение G = Ø + ○G +●G.

Несмотря на то, что умножение некоммутативно, и мы фактически не различаем левое и правое деление, попробуем всё же «решить» это уравнение, на свой страх и риск. Получим,

Учитывая формулу суммы геометрической прогрессии , имеем

.

В этой сумме так же учтены все возможные варианты разбиения в точности по одному разу. Далее воспользуемся формулой бинома Ньютона: , где — число сочетаний из n по k. Тогда с учетом этого имеем:

Коэффициент при ○ k ● n-k равный числу сочетаний из n по k, показывает общее количество последовательностей из n шаров содержащих ○ шары в количеств k штук и ● шары в количестве n-k штук. Таким образом, общее количество расположений n шаров есть сумма по всем возможным значениям k. Как известно .

Обсуждение метода

Так что же позволяет данному методу быть работоспособным при решении различных задач?

Алгоритм решения задачи можно описать примерно следующим образом: рассматривается некоторая бесконечная сумма, которая в конечном итоге представляет собой формальный степенной ряд G(z) = g₀ + g₁z + g₂z 2 +… + g_nz n +… причем коэффициенты g_k (не заданные в явном виде) — являются ключом к решению исходной задачи. То, что ряд является формальным, говорит о том, что z — является просто символом, то есть вместо него может быть любой объект: число, шар, кость домино и т.д. В отличие от степенных рядов в анализе формальным степенным рядам не придается числовых значений и, соответственно, нет смысла говорить о сходимости таких рядов для числовых аргументов.

Затем производя различные преобразования с бесконечной суммой G(z) мы преобразуем её к замкнутому (компактному) виду. То есть у производящей функции есть 2 представления: бесконечное и замкнутое и, как правило, для решения задачи необходимо бесконечный вид преобразовать к замкнутому, а затем замкнутый вид разложить в степенной ряд, и тем самым получить значения для коэффициентов g_k.

А теперь вооружившись знаниями, вернемся к задаче, которую решал Эйлер.

Я не знаю, как долго Эйлер придумывал решение для этой задачи, но оно поражает своей неожиданностью. Посудите сами. Эйлер рассматривает произведение G(z) = (1+z)(1+z 2 )(1+z 4 )… которое после раскрытия скобок представляется в виде бесконечного ряда G(z) = 1 + g₁z + g₂z 2 + g₃z 3 +….

Следующий шаг Эйлера поражает не менее предыдущего. Он умножает обе части равенства на (1-z).

(1-z)G(z) = (1-z)(1+z)(1+z 2 )(1+z 4 )(1+z 8 )…
(1-z)G(z) = (1-z2)(1+z 2 )(1+z 4 )(1+z 8 )…
(1-z)G(z) = (1-z 4 )(1+z 4 )(1+z 8 )…
(1-z)G(z) = 1

С одной стороны G(z) = 1 + g₁z + g₂z 2 + g₃z 3 +… с другой стороны мы только что получили . Последнее равенство есть не что иное, как сумма геометрической прогрессии, которая равна . Сопоставляя эти два равенства, получаем g₁ = g₂ = g₃ =… = 1, то есть любой груз в k грамм можно взвесить гирями в 1, 2, 4, 8,… грамм притом единственным способом.

Решение рекуррентных соотношений

Производящие функции подходят для решения не только комбинаторных задач. Оказывается, с их помощью можно решать рекуррентные соотношения.

Начнем со всеми знакомой последовательностью чисел Фибоначчи. Каждый из нас знает её рекуррентный вид: F₀ = 0, F₁ = 1, F_n = F_n-1 + F_n-2, n ≥ 2. Однако не каждый знает вид этой формулы в замкнутом виде и это не удивительно, ведь она содержит иррациональное число(«золотое сечение») в своём составе.

Просуммируем эти равенства:

Обозначим левую часть

Рассмотрим каждое из слагаемых в правой части:

Имеем следующее уравнение G(z) = z + z G(z) + z 2 G(z) решая которое относительно G(z) находим

— производящая функция для последовательности чисел Фибоначчи.

Разложим её на сумму простейших дробей, для этого найдем корни уравнения . Решая это простое квадратное уравнение, получаем: . Тогда нашу производящую функцию можно разложить следующим образом:

Следующим шагом является нахождение коэффициентов a и b. Для этого умножим дроби на общий знаменатель:

Подставляя в это уравнение значение z = z₁ и z = z₂, находим

Напоследок немного преобразуем выражение для производящей функции

Теперь каждая из дробей представляет собой сумму геометрической прогрессии.

По формуле находим

Но ведь мы искали G(z) в виде . Отсюда делаем вывод, что

Эту формулу можно переписать в другом виде не используя «золотое сечение»:

что достаточно трудно было ожидать, учитывая красивое рекуррентное уравнение.

Давайте запишем общий алгоритм решения рекуррентных уравнений, используя производящие функции. Он записывается в 4 шага:

Прежде чем переходить к следующему примеру, рассмотрим 2 операции, совершаемые над производящими функциями, которые часто оказываются полезными.

Дифференцирование и интегрирование производящих функций

Для производящих функций обычное определение производной можно записать следующим образом.

Пусть G = G(z) – производящая функция. Производной этой функции называется функция . Дифференцирование, очевидно, линейная операция, поэтому для того, чтобы понять, как оно действует на производящих функциях, достаточно посмотреть на его действие, на степенях переменной. Имеем

Тем самым, действие дифференцирования на произвольной производящей функции
G (z) = g₀ + g₁z + g₂z 2 + g₃z 3 +… дает G΄(z) = g₁ + 2g₂z + 3g₃z 2 + 4g₄z 3 +….

Интегралом называется функция

Операция дифференцирования обратна операции интегрирования:

Операция же интегрирования производной приводит к функции с нулевым свободным членом, и поэтому результат, отличается от исходной функции,

Нетрудно заметить, что для функций, представимых в виде степенных рядов, формула для производной соответствует обычной. Формула для интеграла соответствует значению интеграла с переменным верхним пределом

Используя только что полученные знания о дифференцировании и интегрировании производящих функций, попробуем решить следующее рекуррентное уравнение:

Будем следовать вышеописанному алгоритму. Первое условие алгоритма выполнено. Умножим обе части всех равенств на z в соответствующей степени и просуммируем:

z 0 ⋅ g₀ = 1,
z 1 ⋅ g₁ = z,
z n ⋅ g_n = z n ⋅ g_n-1 + 2z n ⋅ g_n-2 + (-1) n ⋅ z n

Левая часть представляет собой производящую функцию в бесконечном виде.

Попытаемся выразить правую часть через G(z). Рассмотрим каждое слагаемое:

Это и есть производящая функция для заданного рекуррентного уравнения. Раскладывая её на простейшие дроби (например, методом неопределенных коэффициентов или методом подстановки различных значений z), получаем:

Второе и третье слагаемые легко раскладываются в степенной ряд, а вот с первым придется чуть повозиться. Используя правило дифференцирования производящих функций имеем:

Собственно всё. Раскладываем каждое слагаемое в степенной ряд и получаем ответ:

С одной стороны мы искали G(z) в виде , с другой стороны .

Значит, .

Вместо заключения

Возводя в квадрат обе части этого равенства получим

Приравнивая коэффициенты при x n в левой и правой частях, получаем

Эта формула имеет прозрачный комбинаторный смысл, но доказать её непросто. Еще в 80-е годы XX века появились публикации, посвященный этому вопросу.

Источник

Персональная страничка
Диканева Тараса
Викторовича

4.1. Рекуррентные соотношения: основные понятия

В основе рассмотренных ранее алгоритмических приемов накопления суммы и произведения лежит фундаментальная идея о том, что результат вычислений на каждом шаге цикла должен зависеть от результата вычислений на предыдущем шаге. Обобщенным математическим выражением этой идеи являются рекуррентные соотношения.

Будем говорить, что последовательность векторов задана рекуррентным соотношением, если задан начальный вектор и функциональная зависимость последующего вектора от предыдущего

Вектора можно интерпретировать как наборы значений переменных. Таким образом, они характеризуют состояние вычислительного процесса. Функцию будем понимать как преобразование значений переменных на каждом шаге цикла.

Пример 1: Запишите рекуррентные соотношения для нахождения суммы целых чисел от 1 до m и факториала m!

Как видно, вычислительные процессы, соответствующие накоплению суммы и произведения действительно могут быть заданы рекуррентными соотношениями.

В приведенных примерах рекуррентные соотношения явно содержали номер шага n, чего, вообще говоря, нет в формуле (1). С практической точки зрения это не важно – в цикле for на каждом шаге можно использовать значение переменной-счетчика шагов. Однако, заботясь о математической строгости, нетрудно свести все к виду (1), сделав номер шага элементом вектора состояния вычислительного процесса. Так для вычисления факториала будем иметь:

Однократное вычисление следующих значений по предыдущим посредством рекуррентных соотношений называется итерацией. А процесс вычислений с помощью рекуррентных соотношений соответственно итерированием.

Источник

Рекурсия и деревья

Во-первых, рекурсивная структура этого решения непосредственно обуславливает количество необходимых перемещений.

Как обычно, из кода немедленно следует, что количество перемещений удовлетворяет условию рекуррентности. В данном случае рекуррентная формула похожа на формулу 2.5:

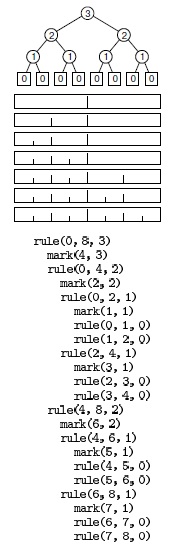
Программа 5.7. Решение задачи о ханойских башнях

Чтобы переместить башню из дисков вправо, мы перемещаем (рекурсивно) все диски, кроме нижнего, влево, потом перекладываем нижний диск вправо, а затем перемещаем (рекурсивно) башню поверх нижнего диска.

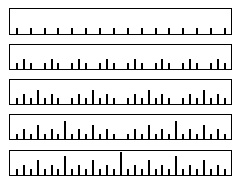
Программа 5.8. Применение алгоритма «разделяй и властвуй » для рисования линейки

Cразу видно, что последовательность длин в точности совпадает с последовательностью перемещаемых дисков при решении задачи о ханойских башнях. Действительно, простым доказательством их идентичности является идентичность рекурсивных программ. То есть для определения перекладываемого диска наши монахи могли бы воспользоваться метками на линейке.

То есть после перекладывания маленького диска на остальных двух стержнях находятся сверху два диска, один из которых меньше другого.

Восходящий подход предполагает изменение порядка выполнения вычислений при рисовании линейки. На рис. 5.11 показан еще один пример, в котором изменен порядок следования трех вызовов функций в рекурсивной реализации. Этот пример соответствует рекурсивному рисованию первоначально описанным способом: нанесение средней метки, затем левой половины, а затем правой. Последовательность нанесения меток выглядит сложной, но является результатом простой перемены мест двух операторов в программе 5.8. Как будет показано в разделе 5.6, взаимосвязь между рис. 5.8 и рис. 5.11 сродни различию между постфиксными и префиксными арифметическими выражениями.

Программа 5.9. Нерекурсивная программа для рисования линейки

Возможно, нанесение меток в порядке, показанном на рис. 5.8, более удобно по сравнению с вычислениями в измененном порядке, которые содержатся в программе 5.9 и приведены на рис. 5.11, поскольку в этом случае можно нарисовать линейку произвольной длины. Достаточно представить себе графическое устройство, которое просто непрерывно перемещается от одной метки к следующей. Аналогично, при решении задачи о ханойских башнях мы ограничены последовательностью перемещений, которая должна быть выполнена. Вообще говоря, многие рекурсивные программы основываются на решениях подзадач, которые должны быть выполнены в конкретном порядке. Для других вычислений (см., например, программу 5.6) порядок решения подзадач роли не играет. Для таких вычислений единственным ограничением служит необходимость решения подзадач перед тем, как можно будет решить главную задачу. Понимание того, когда можно изменять порядок вычисления, не только служит ключом к успешной разработке алгоритма, но и во многих случаях оказывает непосредственное практическое влияние. Например, этот вопрос исключительно важен при реализации алгоритмов для работы на параллельных процессорах.

Восходящий подход соответствует общему методу разработки алгоритмов, при котором задача решается путем решения вначале элементарных подзадач с последующим объединением этих решений для получения решения несколько больших подзадач и т.д., пока вся задача не будет решена. Этот подход можно было бы назвать «объединяй и властвуй «.

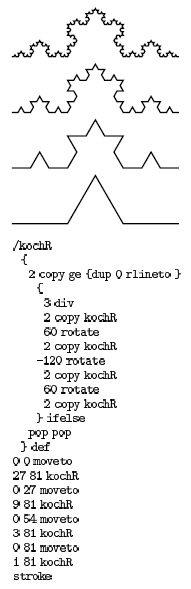
Лишь небольшой шаг отделяет рисование линеек от рисования двумерных узоров, похожих на показанный на рис. 5.12. Этот рисунок показывает, как простое рекурсивное описание может приводить к сложным на вид вычислениям (см. упражнение 5.30).

Для рисования линейки нерекурсивным методом вначале рисуются все метки длиной 1 и пропускаются позиции, затем рисуются метки длиной 2 и пропускаются остающиеся позиции, затем рисуются метки длиной 3 с пропуском остающихся позиций и т.д.

Эта последовательность отображает результат нанесения меток перед рекурсивными вызовами, а не между ними.

Подобно решениям задач рисования линейки и ханойских башен, эти алгоритмы линейны по отношению к количеству шагов, но это количество связано экспоненциальной зависимостью с максимальной глубиной рекурсии (см. упражнения 5.29 и 5.33). Они также могут быть непосредственно связаны с последовательностью натуральных чисел в соответствующей системе счисления (см. упражнение 5.34).

Это изменение программы PostScript, приведенной на рис. 4.3, преобразует результат ее работы в фрактал (см. текст).

Таблица 5.1. Основные алгоритмы типа «разделяй и властвуй »

рекуррентное соотношение	приближенное решение
Бинарный поиск
количество сравнений	CN = CN/2 + 1	lg N
Сортировка слиянием
количество рекурсивных вызовов	AN = 2AN/2 + 1	N
количество сравнений	CN = 2CN/2 + N	NlgN

Заслуживают внимания и следующие разновидности основной темы: разбиение на части различных размеров, разбиение более чем на две части, разбиение на перекрывающиеся части и выполнение различного объема вычислений в нерекурсивной части алгоритма. В общем случае алгоритмы «разделяй и властвуй » требуют выполнения вычислений для разбиения входного массива на части, либо для объединения результатов обработки двух независимо решенных частей исходной задачи, либо для упрощения задачи после того как половина входного массива обработана. То есть, код может находиться перед, после и между двумя рекурсивными вызовами. Естественно, подобные вариации приводят к созданию более сложных алгоритмов, чем бинарный поиск или сортировка слиянием, и эти алгоритмы труднее анализировать. В данной книге будут рассмотрены многочисленные примеры; к более сложным приложениям и способам анализа мы вернемся в части VIII.

5.16. Напишите рекурсивную программу, которая находит максимальный элемент в массиве, выполняя сравнение первого элемента с максимальным элементом остальной части массива (найденным рекурсивно).

5.17. Напишите рекурсивную программу, которая находит максимальный элемент в связном списке.

5.19. Нарисуйте дерево, которое соответствует рекурсивным вызовам, выполняемым программой из упражнения 5.18 при размере массива 11.

5.20. Методом индукции докажите, что количество вызовов функции, выполняемых любым алгоритмом «разделяй и властвуй «, который делит задачу на части, в сумме составляющие задачу в целом, а затем решает части рекурсивно, линейно относительно размера задачи.

5.24. Напишите программу, которая выдает решение задачи о ханойских башнях путем заполнения массива, содержащего все перемещения, как сделано в программе 5.9.

5.27. Докажите следующее свойство программы рисования линейки (программа 5.8): если разность между ее первыми двумя аргументами является степенью 2, то оба ее рекурсивных вызова также обладают этим свойством.

5.28. Напишите функцию, которая эффективно вычисляет количество завершающих нулей в двоичном представлении целого числа.

5.29. Сколько квадратов изображено на рис. 5.12 (включая и те, которые скрыты большими квадратами)?

5.31. Напишите восходящую нерекурсивную программу (аналогичную программе 5.9), которая вычерчивает верхнюю часть рис. 5.12 способом, описанным в упражнении 5.30.

5.35. Измените программу рисования звезды Коха, приведенную на рис. 5.13, для создания другого фрактала, на основе фигуры, состоящей из 5 линий нулевого порядка, вычерчиваемых смещениями на одну условную единицу в восточном, северном, восточном, южном и восточном направлениях (см. рис. 4.3).

5.36. Напишите рекурсивную функцию «разделяй и властвуй » для отображения аппроксимации прямолинейного отрезка в пространстве целочисленных координат для заданных конечных точек. Считайте, что все координаты имеют значения от 0 до M. Совет: вначале поставьте точку вблизи середины сегмента.

Источник