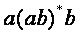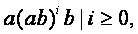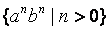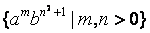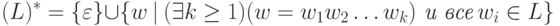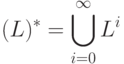что такое регулярный язык

Регулярный язык

В теории языков регуля́рным мно́жеством (или, регуля́рным языком) называется формальный язык, который удовлетворяет приведённым ниже свойствам. Эти простые свойства таковы, что класс регулярных множеств удобно изучать в целом и полученные результаты оказываются применимы во многих важных случаях формальных языков. То есть, понятие регулярного множества является примером математической структуры.

Определение регулярного множества

Пусть Σ — конечный алфавит. Регулярное множество R(Σ) в алфавите Σ определяется следующими рекурсивными свойствами:

№.	Свойство	Описание
1		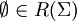Пустое множество является регулярным множеством в алфавите Σ
2		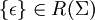Множество, состоящее из одной лишь пустой строки является регулярным множеством в алфавите Σ
3		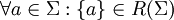Множество, состоящее из одного любого символа алфавита Σ является регулярным множеством в алфавите Σ
4		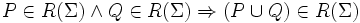Если два какие-либо множества являются регулярными в алфавите Σ, то и их объединение тоже является регулярным множеством в алфавите Σ
5		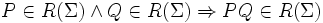Если два какие-либо множества являются регулярными в алфавите Σ, то и множество, составленное из всевозможных сцеплений пар их элементов тоже является регулярным множеством в алфавите Σ
6		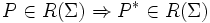Если какое-либо множество является регулярным в алфавите Σ, то множество всевозможных сцеплений его элементов тоже является регулярным множеством в алфавите Σ
Ничто другое, кроме следующего из перечисленного, не является регулярным множеством в алфавите Σ

См. также

Полезное

Смотреть что такое «Регулярный язык» в других словарях:

регулярный язык — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN regular language … Справочник технического переводчика

РЕГУЛЯРНЫЙ — (лат. regularius, от regula правило). Правильный, правильно устроенный, сделанный. Регулярный ход машины. Равномерный ход. Регулярная жизнь. Правильная, порядочная, однообразная жизнь. Словарь иностранных слов, вошедших в состав русского языка.… … Словарь иностранных слов русского языка

регулярный — См … Словарь синонимов

Язык кечуа — Кечуа Самоназвание: Qhichwa Simi, Runa Simi Страны: Аргентина, Боливия, Колумбия, Перу, Чили, Эквадор Регионы: Анды Официальный статус: Перу … Википедия

Древнеписьменный язык — Язык с давними письменными традициями, т. е. получивший письменность, приспособленную к структуре данного языка, несколько веков тому назад, причем функционирование письменного варианта языка носило не эпизодический, а регулярный характер, при… … Словарь социолингвистических терминов

Кечуа (язык) — У этого термина существуют и другие значения, см. Кечуа. Кечуа Самоназвание: Qhichwa Simi, Runa Simi Страны … Википедия

КАРКАС РЕГУЛЯРНЫЙ — каркас здания с сеткой колонг или стоек, основанной на шаге одного размера (Болгарский язык; Български) равномерен скелет (Чешский язык; Čeština) pravidelný skelet (Немецкий язык; Deutsch) regelmäßiges Skelett (Венгерский язык; Magyar) szabályos… … Строительный словарь

ПАРК РЕГУЛЯРНЫЙ — [ПАРК ФРАНЦУЗСКИЙ] парк, имеющий геометрически правильную планировку, обычно осевую схему (Болгарский язык; Български) френски парк (Чешский язык; Čeština) francouzský park (Немецкий язык; Deutsch) regelmäßiger Park; französischer Park… … Строительный словарь

Кечуа язык — Кечуа Самоназвание: Qhichwa Simi, Runa Simi Страны: Аргентина, Боливия, Колумбия, Перу, Чили, Эквадор Регионы: Анды Официальный статус: Перу … Википедия

Тагальский язык — (тагал, тагала, тагало; тагалог) один из филиппинских языков. Ареал первоначального распространения приходится на самый важный в политическом, экономическом и культурном отношении регион Республики Филиппины центральные и южные части острова… … Лингвистический энциклопедический словарь

Источник

Что такое регулярный язык

конспекты занятий по курсу

«Теория и реализация языков программирования»

5. Условия регулярности языка

Строение и некоторые способы задания правильных (регулярных) языков наводит на мысль о возможности создания критерия проверки, с помощью которого можно определить является ли язык правильным. В данном занятии подробно рассматривается вопрос о регулярности конечных языков, а также лемма о накачке для правильных языков (необходимое условие регулярности языка). В конце дана ссылка на материал для изучения теоремы Майхилла-Нероуда, определяющей необходимое и достаточное условие регулярности языка и подробно рассматриваемой на лекции.

Поскольку данное занятие является заключительным по правильным языкам, в конце его приводится ряд задач и примеров из данной области.

5.1. Регулярность конечных языков

Теорема. Конечный язык всегда регулярен.

Действительно, если у нас имеется конечное число ( n ) слов в языке

,

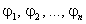
то мы всегда можем предложить для этого языка праволинейную грамматику

,

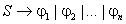
либо регулярное выражение

,

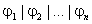
либо известным уже нам способом всегда (хотя бы теоретически) сможем построить для него КА.

Все эти возможности определённо говорят о регулярности произвольного конечного языка.

5.2. Условия регулярности для бесконечного языка

Понятно, что для бесконечного языка применение приведённых в предыдущем разделе приёмов приведёт к началу построения в общем случае бесконечного числа правил грамматики, бесконечного (а не конечного) автомата и т.д., т.е. построения, которое никогда не закончится.

Поэтому для таких языков были разработаны свои критерии, помогающие прояснить вопрос о регулярности соответствующего языка.

5.2.1. Лемма Огдена (лемма о накачке, лемма о разрастании) ( необходимое условие регулярности бесконечного языка)

Эта лемма вытекает из следующих простых соображений.

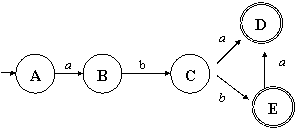
Если у нас есть ДКА, где каждое состояние при исследовании любой из входных цепочек может быть посещено не более одного раза, то понятно, что длина принимаемой цепочки не может превышать числа состояний данного автомата.

Этот автомат никогда не примет цепочку длиннее 4 знаков.

Если же длина принимаемой КА цепочки не меньше, чем число состояний ДКА, то очевидно, что какое-то состояние при разборе данной цепочки было посещено повторно, т.е. данный КА имеет хотя бы одно кольцо (круговорот) состояний, т.е. имеет подмножество состояний, передача управления по которым может происходить по кругу.

Этот автомат может принять цепочку

неограниченно большой длины.

Наличие такого круговорота отражается и в записи соответствующего РВ:

Если переписать это РВ с использованием степени

то можно утверждать, что слово для любого 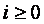будет принадлежать данному РЯ.

В более общем виде это наблюдение можно записать так:

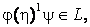
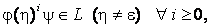
Если цепочку языка можно представить как причём то это один из признаков того, что данный язык – регулярный. Понятно, что цепочка h не должна быть пустой, иначе получим вырожденный случай, выполняющийся для любого языка.

В данном определении не учтено одно обстоятельство. Предваряющая и заключающая цепочки j и y могут быть достаточно длинными, поэтому если возьмём слишком короткое слово, то может так получится, что нам не удастся подобрать соответствующее h даже в регулярном языке (для короткого слова степень его вхождения будет равна нулю). И критерий не сработает.

5.3. Примеры применения леммы о разрастании

Применим данную лемму для языка

Если этот язык регулярен, то для достаточно большого k

ещё более длинную цепочку 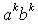можно представить в требуемом леммой виде.

Попробуем это сделать, рассмотрев разные возможности выбора цепочки разрастания h для цепочки, к примеру, .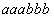

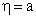
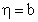
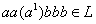
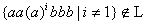
1. Если взять или , то цепочка вида , но , поскольку нарушится соотношение a и b в получаемых словах.

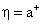
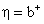
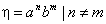
2. По той же причине не выполнится лемма и при выборе или или .

3. Если мы выберем за 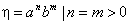, то при возведении h в степень большую 1 у нас нарушится порядок букв в слове.

Поскольку иначе h подобрать для удовлетворения условия леммы также, очевидно, нельзя, то необходимое условие регулярности для данного языка не выполнено и он не является регулярным.

Применим данную лемму для языка

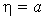
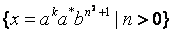
В этом случае для любого допустимого n и любого заранее заданного большого числа k мы можем взять и все слова будут длинной не менее k и принадлежать нашему языку. Т.е. необходимое условие регулярности для этого языка выполнено. В тоже время известно, что данный язык не является регулярным.

Упражнение 5.1. Можно ли утверждать, что за k в вышеприведённой лемме может быть взято число состояний ДКА, задающего исследуемый на регулярность язык (если такой ДКА, разумеется, существует)?

Упражнение 5.2. Как вы думаете – можно ли предложить подобную лемму для контекстно-свободных языков? Если да, то в чём будет их отличие? Сможете ли вы её записать?

5.4. Примеры задач на регулярные языки

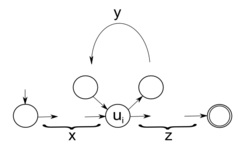
Пример 5.4.1. Построить ДКА для языка < x 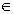<0, 1>* : на каждом кратном двум месте цепочки которого (1, 3, 5, …) стоит знак 0 (нумерация знаков начинается с 1), а | x |₁ – чётно>.

Самые короткие цепочки из данного языка такие:

, 0, 00, 000, 0000, 0101 и т.д.

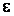
Не будем торопиться переходить к решению этой, в общем-то, простой задачи, а сначала постараемся разобрать её условие, понять, что оно может нам подсказать о будущих свойствах ДКА или ПГ, которые соответствуют данному языку.

Заметим, что в условии задачи указаны два ограничения, одно из которых касается нулей, второе – единиц.

По нулям имеем следующие состояния:

А – мы на кратном двум месте цепочки (начиная с 1-го), здесь должен стоять 0

B – мы на некратном двум месте, здесь может стоять как 0, так и 1.

Источник

Регулярные языки и конечные автоматы

Регулярные выражения и языки

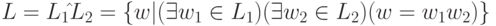
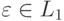
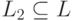
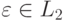
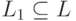
Тогда , т.е. конкатенация языков состоит из конкатенаций всех слов первого языка со всеми словами второго языка. В частности, если , то , а если , то .

Введем обозначения для «степеней» языка L :

Итерацию (L) * языка L образуют все слова которые можно разбить на несколько подряд идущих слов из L :

Ее можно представить с помощью степеней:

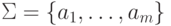
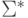
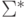
Отметим также, что если рассматривать алфавит как конечный язык, состоящий из однобуквенных слов, то введенное ранее обозначение для множества всех слов, включая и пустое, в алфавите соответствует определению итерации этого языка.

В следующей таблице приведено формальное индуктивное определение регулярных выражений над алфавитом и представляемых ими языков.

Нетрудно проверить, например, такие свойства регулярных операций:

Рассмотрим несколько примеров регулярных выражений и представляемых ими языков.

Пример 5.2. Регулярное выражение (0 +1) * представляет множество всех слов в алфавите <0, 1>.

Пример 5.3. Регулярное выражение 11(0 +1) * 001 представляет язык, состоящий из всех слов в алфавите <0, 1>, которые начинаются на ’11’, а заканчиваются на ‘001’.

Пример 5.4. Регулярное выражение 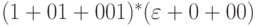представляет язык, состоящий из всех слов в алфавите <0, 1>, которые не содержат подслово ‘000’ ( см. задачу 5.3).

Источник

Доказательство нерегулярности языков: лемма о разрастании

Лемма о разрастании (лемма о накачке, англ. pumping lemma) — лемма, позволяющая во многих случаях проверить, является ли данный язык регулярным.

Содержание

Лемма о разрастании [ править ]

Замечание. Условие леммы не является достаточным для регулярности языка. (См. пример)

Лемма о разрастании в общем виде [ править ]

Исходя из формулировки леммы в общем виде, стандартная версия леммы, которая описана выше, является особым случаем, в котором строки [math]u[/math] и [math]v[/math] пусты.

Доказательство леммы в общем виде аналогично доказательству стандартной версии леммы, с тем отличием, что строки [math]u[/math] и [math]v[/math] теперь могут быть как не пусты, так и пусты.[math]\triangleleft[/math]

Использование леммы для доказательства нерегулярности языков [ править ]

Пример нерегулярного языка, для которого выполняется лемма о разрастании [ править ]

Пример языка, удовлетворяющего стандартной версии леммы [ править ]

Рассмотрим следующий язык: [math]L= \< a^b^c^ \mid i \ne 1, j \geqslant 0, k \geqslant 0\> \cup \< ab^c^ \mid i \geqslant 1\>[/math]

Таким образом, язык [math] L [/math] удовлетворяет второй части леммы и при этом является нерегулярным, что доказывает тот факт, что лемма о разрастании не является достаточным для регулярности языка.

Пример языка, удовлетворяющего лемме в общем виде [ править ]

Рассмотрим другой пример.

[math]L = L_1 \cup L_2[/math]

Источник

Регулярные выражения

В начале лекции даются необходимые определения. Затем в разделе 5.2* приводятся некоторые тождества регулярных выражений, такие как ассоциативность конкатенации, дистрибутивность конкатенации относительно объединения и др. В разделе 5.3 доказывается, что регулярные выражения задают в точности класс автоматных языков. В разделе 5.4* формулируется теорема о классификации автоматных языков по их сложности, измеряемой звездной высотой (необходимой глубиной вложенности итераций при задании данного языка регулярным выражением).

5.1. Определение регулярного выражения

Определение 5.1.1. Регулярное выражение над алфавитом определяется рекурсивно следующим образом: 0 является регулярным выражением; 1 является регулярным выражением; если , то a является регулярным выражением; если e и f являются регулярными выражениями, то , и тоже являются регулярными выражениями.

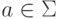
Для экономии скобок будем считать, что операция * связывает сильнее (то есть имеет более высокий приоритет), чем умножение, а умножение связывает сильнее, чем сложение. Вместо часто пишут просто .

Пример 5.1.2. Пусть . Тогда является регулярным выражением над алфавитом .

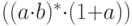
Пример 5.1.4. Пусть . Согласно определению

Определение 5.1.5. Язык L называется регулярным если он задается некоторым регулярным выражением.

Упражнение 5.1.7. Упростить регулярное выражение ((a+bc) * ) *

Упражнение 5.1.8. Найти праволинейную грамматику для языка ab * a

5.2*. Свойства регулярных выражений

Равенство понимается как равенство языков, задаваемых регулярными выражениями.

Лемма 5.2.2. Для любых регулярных выражений e и f выполняются следующие тождества:

Источник