что такое ребро фигуры
Ребро (геометрия)
Связанные понятия
Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.
Упоминания в литературе
Связанные понятия (продолжение)
Пра́вильный двадцатичетырёхъяче́йник, или просто двадцатичетырёхъяче́йник, или икоситетрахор (от др.-греч. εἴκοσι — «двадцать», τέτταρες — «четыре» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве.
Пра́вильный шестнадцатияче́йник, или просто шестнадцатияче́йник — один из правильных многоячейников в четырёхмерном пространстве. Известен также под другими названиями: гексадекахор (от др.-греч. ἕξ — «шесть», δέκα — «десять» и χώρος — «место, пространство»), четырёхмерный гиперокта́эдр (поскольку является аналогом трёхмерного октаэдра), четырёхмерный кокуб (поскольку двойственен четырёхмерному гиперкубу), четырёхмерный ортоплекс.
В геометрии политоп (многогранник, многоугольник или замощение, например) изогонален или вершинно транзитивен, если, грубо говоря, все его вершины эквивалентны. Отсюда следует, что все вершины окружены одним и тем же видом граней в том же самом (или обратном) порядке и с теми же самыми углами между соответствующими гранями.
Если дано топологическое пространство и группа действий на нём, образы отдельной точки под действием группы действий образуют орбиты действий. Фундаментальная область — это подмножество пространства, которое содержит в точности по одной точке из каждой орбиты. Она даёт геометрическую реализацию абстрактного множества представителей орбит.
Многогранник размерности 3 и выше называется изоэдральным или гране транзитивным, если все его грани одинаковы. Точнее сказать, все грани должны быть не просто конгруэнтны, а должны быть транзитивны, то есть должны прилежать в одной и той же орбите симметрии. Другими словами, для любых граней A и B должна существовать симметрия всего тела (состоящая из вращений и отражений), которая отображает A в B. По этой причине выпуклые изоэдральные многогранники имеют формы правильных игральных костей.
В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с ним только вращениями и параллельными переносами. Хиральная фигура и её зеркальный образ называют энантиоморфами. Слово хиральность происходит от др.-греч. χειρ (хеир) — «рука». Это самый известный хиральный объект. Слово энантиоморф происходит от др.-греч. εναντιος (энантиос) — «противоположный», и μορφη (морфе) — «форма». Нехиральный.
Полуправильные многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки, например: все грани равны, или все грани являются правильными многоугольниками, или имеются определённые пространственные симметрии. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.
Пра́вильный пятияче́йник, или просто пятияче́йник, или пентахор (от др.-греч. πέντε — «пять» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве: правильный четырёхмерный симплекс.
Ребро
Религия
В христианской традиции считается, что первая женщина — Ева — была создана Богом из ребра первого человека (Адама).
Ссылки
 |
 Кости человека Кости человека | ||||||||
|---|---|---|---|---|---|---|---|---|
| Череп |
| 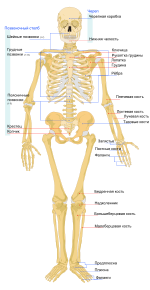 | ||||||
| Позвоночник | Позвонок · Шейные позвонки (Атлант · Эпистрофей) · Грудные позвонки · Поясничные позвонки · Крестец · Копчик | |||||||
| Верхняя конечность |
| |||||||
| Грудная клетка | Грудина · Рёбра | |||||||
| Плечевой пояс | Ключица · Лопатки | |||||||
| Таз | Тазовая кость (Лобковая кость · Подвздошная кость · Седалищная кость) | |||||||
| Нижняя конечность |
| |||||||
Полезное
Смотреть что такое «Ребро» в других словарях:
РЕБРО — ср. реберце, ребрецо, ребрышко; ребришко; ребрище или ребрина жен. край, кромка, ость, гребень, острая грань, щипец, острый или узкий бочок вещи. Ребро доски, узкий край, в толщину. Став ребром, ·противоп. клади плашмя или ставь торцом, стоймя.… … Толковый словарь Даля
ребро — забирать за десятое ребро, задевать за десятое ребро, задирать за десятое ребро, зацепить за десятое ребро, последняя копейка ребром, поставить ребром, ставить вопрос ребром, схватить за десятое ребро, трогать за десятое ребро.. Словарь русских… … Словарь синонимов
ребро — а; мн. рёбра, рёбер, рёбрам; ср. 1. Одна из парных дугообразных плоских костей, идущих от позвоночника к грудной кости и образующих грудную клетку. Грудинные рёбра. Сломать р. Рёбра выпирают, проступают. Повреждение ребра. Одни рёбра остались у… … Энциклопедический словарь
ребро — мн. рёбра, укр. ребро, народн. лебро, др. русск., ст. слав. ребро πλευρά (Остром., Супр.), болг. ребро, сербохорв. рѐбро, мн. ре̏бра, словен. rẹbro, чеш. řebro, žеbrо, слвц. rebro, польск. żebro, в. луж. rjebɫo, н. луж. robro, rоbɫо, полаб.… … Этимологический словарь русского языка Макса Фасмера
РЕБРО — РЕБРО, ребра, мн. рёбра, рёбер, рёбрам, ср. 1. Дугообразная узкая кость, прикрепленная сзади к позвоночнику и идущая к грудной кости. У человека семь верхних и пять нижних, или ложных, ребер. Так похудел, что ребра видно. 2. Линия пересечения… … Толковый словарь Ушакова
ребро — РЕБРО1, а, мн рёбра, род. рёбер, дат. рёбрам, ср Часть скелета человека и животных, представляющая собой одну из парных дугообразных костей, идущих от позвоночника к грудной кости и составляющих грудную клетку. Кроме валунов, здесь было также… … Толковый словарь русских существительных
ребро — ребро, рёбра, ребра, рёбер, ребру, рёбрам, ребро, рёбра, ребром, рёбрами, ребре, рёбрах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов
РЕБРО — РЕБРО, а, мн. рёбра, рёбер, рёбрам, ср. 1. Одна из нескольких парных дугообразных плоских костей, идущих от позвоночника к грудной кости и составляющих грудную клетку. Грудинные рёбра. Шейное р. Поясничное р. Одни рёбра остались у кого н. (перен … Толковый словарь Ожегова
РЕБРО — многогранника см. Многогранник … Большой Энциклопедический словарь
РЕБРО — РЕБРО, длинная и плоская изогнутая кость, набор которых образует каркас грудной клетки позвоночных. Ребра располагаются парами и расходятся в обе стороны от позвоночника. У людей 12 пар ребер. Первые семь пар, так называемые истинные ребра,… … Научно-технический энциклопедический словарь
ребро́ — ребро, а; мн. рёбра, рёбер, рёбрам … Русское словесное ударение
Что такое куб: определение, свойства, формулы
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем
Объем куба равен длине его ребра, возведенной в куб.
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
Многогранники
Математика. 4 класс
Тема. «Многогранник. Элементы многогранника – грани, вершины, ребра».
Цели. Создать условия для расширения теоретических знаний о пространственных фигурах: ввести понятия «многогранник», «грани», «вершина», «ребро»; обеспечить развитие у школьников умения выделять главное в познавательном объекте; содействовать развитию пространственного воображения учащихся.
Учебные материалы. Учебник «Математика. 4 класс» (авт. В.Н. Рудницкая, Т.В. Юдачева); компьютер; проектор; презентация «Многоугольники»; печатные бланки «Координатный угол», «Многоугольники», «Задача»; модели многогранников, развертки многогранников; зеркала; ножницы.
Перед началом урока дети распределяются на три группы соответственно уровню знаний – высокий, средний, низкий.
I. Организационный момент
Учитель. Дорогие мои непоседы, в очередной раз я приглашаю вас в увлекательный мир математики. И я уверена в том, что и на этом уроке вы узнаете новое, закрепите изученное и сможете полученные знания применить на практике.
Сегодня наш урок мне хочется начать словами английского философа Роджера Бэкона о математике: «Тот, кто не знает математики, не может изучить другие науки и не может познать мир». Я думаю, что на уроке мы непременно найдем подтверждение словам этого философа.
II. Повторение пройденного материала. Построение многоугольников по координатам
У. На уроках математики в 1-м, 2-м, 3-м классах мы изучали различные плоские геометрические фигуры, а также учились их строить. Я предлагаю вам построить в координатном угле плоские фигуры по данным координатам.
Задание выполняется на печатных бланках.
Постройте фигуру, если известны координаты А (0; 2), В (2; 5), С (9; 2). Какая фигура получилась?
Постройте прямоугольник, если точки А (3; 2) и В (6; 5) – его противоположные вершины. Назовите координаты противоположных вершин. Как по-другому называется эта фигура?
Постройте фигуру, если известны координаты ее вершин А (2; 3), В (2; 6), С (5; 8), D (8; 6), K (8; 3), М (5; 1). Какая фигура получилась?
– Как можно назвать все эти фигуры?
Дети. Это многоугольники.
У. Нам известно, что все многоугольники имеют вершины и стороны. Назовите и покажите их.
По одному человеку от группы выполняют задание у доски.
III. Знакомство с новым материалом
У. Сегодня я познакомлю вас с объемными геометрическими фигурами, которые называются многоугольниками. Их модели представлены у вас на столах.
На столах у учащихся объемные фигуры: куб, параллелепипед, пирамиды, призмы.
– Садитесь поудобнее, смотрите внимательно, слушайте старательно и запоминайте.
Знакомство с понятиями «многогранник», «грань», «вершина», «ребро»
– Если взять 4 треугольника, то можно создать объемную фигуру – пирамиду. Из квадратов можно получить другую фигуру – куб, из прямоугольников – параллелепипед. У вас на столе еще одна фигура – призма, которая составлена из прямоугольников и треугольников. Все эти фигуры называются многогранниками.
Каждый из многоугольников (в данном случае треугольников) называют гранью многогранника. А стороны многоугольников называют ребрами многогранника. И, конечно же, вершины многоугольника будут вершинами многогранника. Вот так выглядит чертеж многогранника на листе бумаги.
– Кажется, что фигура сделана из стекла. Как вы думаете, что изображено пунктиром на чертеже?
Дети работают по рисунку у доски.
У. Назовите и покажите грани многогранника, его ребра и вершины.
Дети показывают указкой и перечисляют.
– Если разрезать пирамиду с вершины до основания по ребрам, то получится вот такая развертка.
А теперь, дорогие мои непоседы, отыщите на столе бланк с изображением многоугольника, внимательно прочитайте инструкцию:
– На доске представлены развертки многогранников. Попробуйте по чертежу отыскать развертку своей фигуры и собрать многогранник. Работайте вместе, и, я думаю, у вас все получится.
Проверка выполнения задания (слайды 3, 4, 5).
вершин – 8; ребер – 12; граней – 6;
вершины – M, B, C, A, X, K, O, T;
ребра – MB, MA, MT, TX, TO, XK, XA, KO, KC, CB, AC, BO;
грани – MBOT, MBCA, KCBO, TXKO, ACKX, MAXT.
вершин – 8; ребер – 12; граней – 6;
вершины – M, B, C, A, X, K, O, T;
ребра – MB, MA, MT, TX, TO, XK, XA, KO, KC, CB, AC, BO;
грани – MBOT, MBCA, KCBO, TXKO, ACKX, MAXT.
вершин – 12; ребер – 18; граней – 8;
вершины – Y, B, A, X, N, M, P, E, D, F, L, C;
ребра – YB, YX, BA, XA, XN, NM, AM, ME, EP, NP, ED, PF, DF, FL, LC, CD, LY, CB;
грани – BAMEDC, YXNPFL, YBAX, XAMN, NMEP, EDFP, DFLC, CLYB.
IV. Обобщение и систематизация знаний
У. Скажите, есть ли в окружающем нас мире предметы, которые имеют форму многогранников?
Выслушиваются ответы детей. Проводится импровизированная «прогулка» по школьному двору. Дети «рассматривают» модели школьного здания, подсобных помещений, которые имеют вид многогранников.
Волк и Заяц склеили из цветной бумаги домик. Сколько граней каждого цвета потребовалось? Форму какого многоугольника имеет грань каждого цвета?
Волк и Заяц склеили из цветной бумаги модель нового здания нашей школы.
Сколько граней имеет модель здания?
Форму какого многоугольника имеет грань каждого цвета?
Сколько граней каждого цвета понадобилось?
V. Закрепление ранее изученного
У. Ребята, представьте себя архитекторами, дизайнерами или строителями и попробуйте решить задачи.
Задание для группы 1
Найдите площадь, которую будет занимать новое школьное здание, если его длина 74 м, а ширина – 13 м. (Ответ: 962 кв. м.)
Задание для группы 2
Площадь игровой площадки во дворе нашей школы равна 1080 кв. м. Это на 1320 кв. м меньше, чем площадь хоккейной площадки. Вычислите площадь хоккейной площадки. (Ответ: 2400 кв. м)
Задание для группы 3
Под строительство нового здания для нашей школы отведен участок площадью 2500 кв. м. Известно, что здание будет шириной 13 м, длиной 74 м. Какая площадь участка останется под цветники и дорожки после постройки здания? (Ответ: 1) 962 кв. м; 2) 1538 кв. м)
Дети проверяют решения задач, объясняют, как решали.
VI. Итог урока
У. Оказывается, Роджер Бэкон был прав, сказав: «Тот, кто не знает математики, не может изучить другие науки и не может познать мир».
Значение слова ребро
Словарь Ушакова
1. Дугообразная узкая кость, прикрепленная сзади к позвоночнику и идущая к грудной кости. У человека семь верхних и пять нижних, или ложных, ребер. Так похудел, что ребра видно.
2. Линия пересечения двух плоскостей (мат.). Ребро многогранника. Ребро двугранного угла.
Архитектурный словарь
(Архитектура: иллюстрированный справочник, 2005)
Фразеологический словарь русского языка
Фразеологический словарь (Волкова)
► Там ему рёбра пересчитают, пусть только явится!
Словарь музыкальных терминов
горизонтальная черта, соединяющая несколько восьмых нот. Двойное рёбро соединяет шестнадцатые ноты, тройное — тридцать вторые и т. д.
Словарь охотничьих терминов и выражений
вся грудная клетка борзой.
Словарь Ожегова
РЕБРО, а, мн. рёбра, рёбер, рёбрам, ср.
1. Одна из нескольких парных дугообразных плоских костей, идущих от позвоночника к грудной кости и составляющих грудную клетку. Грудинные рёбра. Шейное р. Поясничное р. Одни рёбра остались у когон. (перен.: очень исхудал; разг.). Пересчитать рёбра комун. (перен.: поколотить; прост.).
2. В геометрии: отрезок прямой, лежащий на пересечении двух граней многогранника.
3. Узкий край или сторона предмета. Поставить доску на р.
4. Дугообразно изогнутая скрепляющая часть остова какогон. сооружения (спец.).
• Поставить вопрос ребром (разг.) заявить о чёмн. со всей решительностью.
| уменьш. рёбрышко, а, ср. (к 1 знач.).
| прил. рёберный, ая, ое (к 1 знач.) и ребровый, ая, ое (ко 2 и 3 знач.; спец.).















