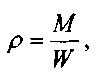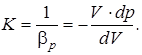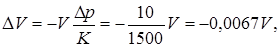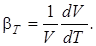что такое реальная жидкость
Чем отличается идеальная жидкость от реальной
Чтобы легче усваивать законы движения жидкости, ученые ввели понятие «идеальная и реальная жидкость».
Идеальная – невязкая жидкость. В ней нет сил трения, касательных напряжений, поэтому под воздействием внешних сил такая жидкость не изменяется в объеме. В реальной жизни такой жидкости не существует.
Реальной жидкостью называется жидкость, характеризующаяся вязкостью. В ней присутствуют силы трения и напряжения. Поэтому она сжимается, сопротивляется, обладает подвижностью.
Вязкость и реальная жидкость
Любой реальной жидкости присуща определенная степень вязкости. Благодаря этому при относительном сдвиге смежных частиц жидкости возникает внутреннее трение. Существуют легко подвижные жидкости – воздух, вода. Какие жидкости называют реальными высоковязкими? Те, в которых сопротивление сдвигу значительно. Это тяжелые масла, глицерин.
Вязкость характеризует подвижности частиц жидкости, ее текучесть. На этом построен закон внутреннего трения Ньютона. По нему при течении жидкости между ее слоями образуются касательные напряжения, которые пропорциональны градиенту скорости.
Реальные жидкости делятся на:
Ньютоновские реальные жидкости это жидкости, при движении одного слоя которых относительно другого величина касательных напряжений (внутреннего трения) пропорциональна скорости сдвига. При относительном покое эти напряжения равны нулю.
Неньютоновские. Обладают большой подвижностью и отличаются от ньютоновских жидкостей наличием касательных напряжений (внутреннего трения) в состоянии покоя, величина которых зависит от вида жидкости.
Основные физические свойства реальных жидкостей
Также к свойствам относятся газосодержание, испарение, кипение, теплоемкость и др.
Информация о реальной жидкости – это в гидравлике теоретическая основа. Законы равновесия и движения жидкости, эксперименты, связанные с ними, позволяют решать инженерные задачи. Полученные расчеты и выводы применяются при конструировании систем кондиционирования, вентиляции, газопроводов.
Понятие жидкости. Реальная и идеальная жидкости
Предмет гидравлики и краткая история её развития.
Введение
Содержание
1.1 Предмет гидравлики и краткая история её развития.
1.4 Общие уравнения сплошной среды
1.5 Потери напора при установившемся движении.
2. Объемные гидромашины.
2.1 Понятие объемной гидромашины. Насосы, гидродвигатели.
2.2 Величины характеризующие рабочий процесс ОГМ.
2.3 Роторные гидромашины. Классификация.
3. Основные сведения об оъемном гидроприводе.
3.1 Назначения и основные свойства
3.2 Основные параметры гидрооборудования.
3.3 Основные режимы работы и условия эксплуатации гидрооборудования.
Раздел механики, в котором изучают равновесие и движение жидкости, а также силовое взаимодействие жидкостью и обтекаемыми ею телами или ограничивающими её поверхностями, называется гидромеханикой.
Науку о законах равновесия и движения жидкостей и о способах приложения этих законов к решению практических задач называют гидравликой. В гидравлике рассматривают, главным образом, потоки жидкости, ограниченные и направленные твердыми стенками, т. е. течение в закрытых и открытых каналах.
Таким образом, можно сказать, что в гидравлике изучают в основном внутренние течения жидкостей и решают так называемую внутреннюю задачу в отличие от внешней, связанной с внешним обтеканием тел сплошной средой, которое имеет место при движении тела в жидкости или газе.
Историческое развитие механики жидкостей шло двумя различными путями:
— первый путь – теоретический, путь точного математического анализа, основанного на законах механики. Он привел к созданию теоретической гидромеханики, которая долгое время являлась самостоятельной дисциплиной, непосредственно не связанная с экспериментом. Однако на пути чистого теоретического исследования движения жидкости встречается множество трудностей, и методы теоретической гидромеханики не всегда дают ответы на вопросы, выдвигаемые практикой.
— второй путь – путь широкого применения эксперимента и накопления опытных данных для использования их в инженерной практике – привел к созданию гидравлики.
Жидкость – физическое тело, молекулы которого слабо связаны между содой. Поэтому незначительные силы способны легко изменить форму жидкости, которая способна сохранить объем, но не форму. В гидравлике жидкость рассматривают как непрерывную среду, заполняющую пространство без пустот и промежутков, т.е. отвлекаются от молекулярного строения жидкости и её частицы, даже бесконечно малые, считают состоящими из большого числа молекул.
Реальной жидкостью называют жидкость, обладающую вязкостью (свойство жидкости сопротивляться сдвигу ее слоев).
Идеальная или невязкая жидкость является упрощенной моделью реальной (вязкой) жидкости. По предположению, идеальная жидкость имеет все свойства реальной, кроме вязкости.
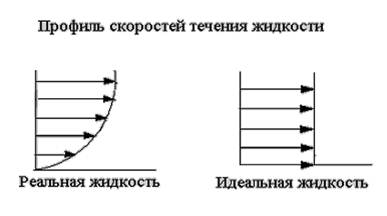
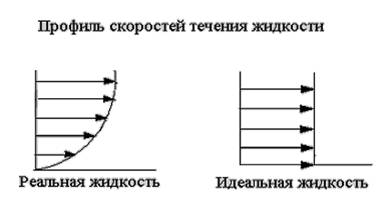
рис. 1.1 Профиль скоростей течения жидкости.
Реальная и идеальная жидкости
Жидкость– физическое тело, молекулы которого слабо связаны между собой. Поэтому незначительные силы способны легко изменить форму жидкости, которая способна сохранить объем, но не форму. В гидравлике жидкость рассматривают как непрерывную среду, заполняющую пространство без пустот и промежутков, т.е. отвлекаются от молекулярного строения жидкости и её частицы, даже бесконечно малые, считают состоящими из большого числа молекул.
Реальной жидкостью называют жидкость, обладающую вязкостью (свойство жидкости сопротивляться сдвигу ее слоев).
Идеальная или невязкая жидкость является упрощенной моделью реальной (вязкой) жидкости. По предположению, идеальная жидкость имеет все свойства реальной, кроме вязкости.
5.Физические свойства жидкостей
Физические свойства характеризуются температурным расширением, сжимаемостью, упругостью, испаряемостью и вязкостью.
Температурное расширение – это свойство жидкости изменять свой объем при изменении температуры
Сжимаемость жидкостей– это свойство жидкостей изменять свой объем при изменении давления
Упругость жидкостей – это способность жидкости принимать свой прежний объем после снятия внешней нагрузки. Такое свойство жидкости характеризуется коэффициентом упругости e= 1/bp. Свойство упругости определяет использование жидкости в качестве рабочего тела во многих гидравлических устройствах и в машинах и характеризуется модулем упругости К, Н/м.
Испаряемость. Испаряемость присуща всем жидкостям, но в различной степени, причем она сильно зависит от условий, в которых находится жидкость. Одной из характеристик испаряемости является температура кипения при нормальном атмосферном давлении. Но атмосферное давление – это лишь частный случай давления в гидросистеме, поэтому более полной характеристикой испаряемости являетсядавление (упругость) насыщенных паровpн.п.. Чем выше pн.п, тем более летучая жидкость. С ростом температуры оно возрастает, но для разных жидкостей в различной степени. Поэтому даже сухой воздух в квартире зимой при контакте с предметом, занесенным с мороза, при остывании становится влажным, и из него конденсируются капельки воды. Это хорошо знают люди, носящие очки. Образование конденсата можно наблюдать на поверхности труб, по которым подается холодная вода, на оконных стеклах и т.п.
Вязкость жидкостей–это свойство жидкостей оказывать сопротивление перемещению слоев жидкости относительно друг друга. Вязкость есть свойство противоположное текучести: более вязкие жидкости (глицерин, масла и т.п.) являются менее текучими и наоборот.
При течении вязкой жидкости вдоль твердой стенки происходит торможение потока, обусловленное вязкостью жидкости. Скорость потока отдельных слоев уменьшается по мере приближения слоя жидкости к стенке.
Вязкость капельных жидкостей в значительной мере зависит от температуры. Например, с повышением температуры вязкость капельной жидкости уменьшается, а воздуха увеличивается.
Абсолютная и относительная плотность жидкости
Важнейшим физическим свойством жидкости, определяющим её концентрацию в пространстве, является плотность жидкости. Под плотностью жидкости понимается масса единицы объёма жидкости:
Исключительными особенностями обладает вода, максимальная плотность которой отмечается при 4 °С
Относительной плотностью вещества называют отношение плотности исследуемого вещества к плотности эталонного вещества. В качестве эталонной жидкости чаще всего используют дистиллированную воду, плотность которой при +20 °C равна 998,203 кг/м3, а при температуре максимальной плотности (+4 °C) составляет 999,973 кг/м3.
Определяют относительную плотностьпри помощи пикнометра, взвешивая сначала пустой пикнометр, затем пикнометр с дистиллированной водой, а потом пикнометр с исследуемой жидкостью.
7. Сжимаемость.Сжимаемость –это свойство жидкости изменять свой объем под действием давления. Сжимаемость характеризуется двумя величинами: коэффициентом объемного сжатия bp и объемным модулем упругости K.
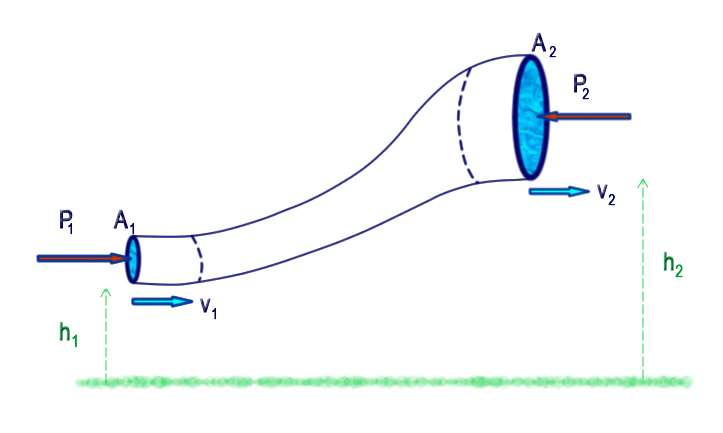
Коэффициент объемного сжатия – это относительное изменение объема жидкости, приходящееся на единицу давления
.
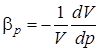
Знак “минус” в этом выражении введен для того, чтобы этот коэффициент имел положительные значения, так как производная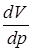 
всегда отрицательная.
Если принять, что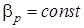 
, то можно приближенно рассчитать объем и плотность жидкости при изменении давления:
Величина, обратная коэффициенту объемного сжатия, называется объемным модулем упругости
Объемный модуль упругости несколько возрастает при повышении давления и немного снижается при росте температуры. Оценим сжимаемость капельных жидкостей. При атмосферном давлении для минеральных масел K » 1320 – 1720 МПа. При повышении давления на 10 МПа (приблизительно 100 ат) изменение объема минерального масла составит примерно
то есть изменение объема жидкости при столь существенном изменении давления составило 0,67%. По этой причине в гидравлике очень часто жидкость считают несжимаемой.
Для воды коэффициент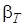 
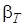
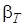
при увеличении температуры возрастает. Рост давления при низких температурах приводит к увеличению , а при температурах выше 50°С – к его снижению. Для большинства других капельных жидкостей с ростом давления уменьшается.
В конечной форме при bT = const (при малом изменении температуры)
; 
,
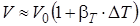
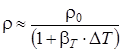
где DT = T – T0 – изменение температуры жидкости.
Изменение объема при нагревании жидкостей весьма ощутимо, поэтому его необходимо учитывать при проектировании гидравлических устройств, в которых жидкость существенно нагревается.
Дата добавления: 2018-05-02 ; просмотров: 4580 ; Мы поможем в написании вашей работы!
Идеальная жидкость и уравнения, описывающие ее движение
Раздел физики, который изучает особенности движение жидких сред, называется гидродинамикой. Одним из главных математических выражений гидродинамики является уравнение Бернулли для идеальной жидкости. Именно этой теме посвящена статья.
Что такое идеальная жидкость?
Многие знают, что жидкая субстанция представляет собой такое агрегатное состояние материи, которое сохраняет при постоянных внешних условиях объем, но изменяет свою форму при малейшем воздействии на нее. Под идеальной жидкостью понимают такую текучую субстанцию, которая не имеет вязкости и является несжимаемой. Это два главных свойства, которые отличают ее от реальных текучих сред.
Вам будет интересно: Как разобрать предложение по составу? Русский язык
Отметим, что практически все реальные жидкости можно считать несжимаемыми, поскольку для небольшого изменения их объема необходимо огромное внешнее давление. Например, если создать давление в 5 атмосфер (500 кПа), то вода увеличит свою плотность всего на 0,024 %. Что касается вопроса вязкости, то для ряда практических задач, когда в качестве рабочей жидкости рассматривается вода, ею можно пренебречь. Для полноты информации отметим, что динамическая вязкость воды при 20 oC составляет 0,001 Па*с2, что в сравнении с этой величиной для меда (>2000), является мизерным значением.
Важно не путать понятия идеальной жидкости и идеального газа, поскольку последний является легко сжимаемым.
Уравнение непрерывности
В гидродинамике движение идеальной жидкости начинают рассматривать с изучения уравнения непрерывности ее потока. Чтобы понять суть вопроса, необходимо рассмотреть движение жидкости по трубе. Представим, что на входе труба имеет площадь сечения A1, а на выходе A2.
Теперь предположим, что жидкость течет в начале трубы со скоростью v1, это означает, что за время t через сечение A1 пройдет поток объемом V1 = A1*v1*t. Поскольку жидкость является идеальной, то есть несжимаемой, то точно такой же объем воды должен выйти из конца трубы за время t, получаем: V2 = A2*v2*t. Из равенства объемов V1 и V2 следует уравнение непрерывности потока идеальной жидкости:
Из полученного уравнения следует, что если A1>A2, то v1 должно быть меньше, чем v2. Другими словами, уменьшая сечение трубы, мы тем самым увеличиваем скорость выходящего из нее потока жидкости. Очевидно, что этот эффект наблюдал каждый человек в жизни, кто хотя бы раз поливал из шланга клумбы с цветами или огород, так, прикрывая пальцем отверстие шланга, можно наблюдать, как струя бьющей из него воды становится сильнее.
Уравнение непрерывности для разветвленной трубы
Интересно рассмотреть случай движения идеальной жидкости по трубе, которая имеет не один, а два и более выхода, то есть является разветвленной. Например, площадь сечения трубы на входе равна A1, а к выходу она разветвляется на две трубы с сечениями A2 и A3. Определим скорости потоков v2 и v3, если известно, что на вход вода поступает со скоростью v1.
Используя уравнение непрерывности, получаем выражение: A1*v1 = A2*v2 + A3*v3. Чтобы решить это уравнения относительно неизвестных скоростей, нужно понимать, что на выходе, в какой бы трубе не находился поток, он движется с одинаковой скоростью, то есть v2=v3. Этот факт можно понять интуитивно. Если разделить некоторой перегородкой выходную трубу на две части, скорость потока при этом не изменится. Учитывая этот факт, получаем решение: v2 = v3 = A1*v1/(A2 + A3).
Уравнение Бернулли для идеальной жидкости
Швейцарский физик и математик голландского происхождения Даниил Бернулли в своей работе «Гидродинамика» (1734 год) представил уравнение идеальной жидкости, описывающее ее движение. Оно записывается в следующей форме:
P+ ρ*v2/2 + ρ*g*h = const.
Напомним, что это уравнение справедливо для идеальной жидкости. В действительности же всегда существует трение текучей субстанции о стенки трубы и внутри ее объема, поэтому в приведенное уравнение Бернулли вводят дополнительный член, описывающий эти энергетические потери.
Использование уравнения Бернулли
Интересно привести некоторые изобретения, в которых используются выводы из уравнения Бернулли:
Режимы течения жидкости
Уравнение Бернулли не учитывает режим движения жидкости, который может быть двух типов: ламинарный и турбулентный. Ламинарный поток характеризуется спокойным течением, при котором слои жидкости движутся по относительно плавным траекториям и не смешиваются между собой. Турбулентный режим движения жидкости характеризуется хаотичным перемещением каждой молекулы, составляющей поток. Особенностью турбулентного режима является наличие завихрений.
Каким способом будет течь жидкость, зависит от ряда факторов (особенности системы, например, наличия или отсутствия шероховатостей на внутренней поверхности трубы, вязкости субстанции и скорости ее перемещения). Переход между рассматриваемыми режимами движения описывается числами Рейнольдса.
Что такое реальная жидкость
Ежедневно на улицах городов мы видим людей, выдыхающих большое количество пара, использующих для этого специальные устройства.
Вейперов делят на 2 группы:
Цели курильщиков электронных сигарет:
Курильщики считают курение электронных устройств абсолютно безопасной имитацией курения, но все чаще в различных источниках публикуются материалы, в которых говорится о том, что вред от курения электронных сигарет сравним с вредом от курения обычных.
Вейп можно сравнить с ингалятором, в котором при закипании жидкости образуется пар, который вдыхает курильщик.
Из чего состоит жидкость для парения?
Вейперы считают, что :
НО отсутствие канцерогенных смол не может сделать устройство для парения абсолютно безопасным.
Что мы имеем на самом деле?
Воздействие на организм:
Кому ни в коем случае нельзя курить электронные сигарет любых видов?
Каждый курильщик электронных устройств обязан знать, что:
Всемирная организация здравоохранения (ВОЗ) относит электронные сигареты к электронным системам доставки никотина и отмечает, что их применение недостаточно исследовано в отношении безопасности и эффективности в качестве средства лечения никотиновой зависимости.
Курение вредит здоровью, последствия курения проявляются позже.