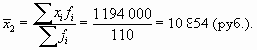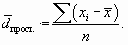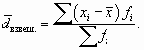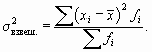что такое размах вариации в статистике
Вариация, размах, межквартильный размах, среднее линейное отклонение
В этой статье мы приступим к изучению показателей вариации: размах вариации, межквартильный размах, среднее линейное отклонение.
В математической статистике вариация занимает одно из центральных мест. Что же такое вариация? Это изменчивость. Вариация показателя – изменчивость показателя.
Показатели вариации дают очень важную характеристику процессам и явлениям. Они отражают устойчивость процессов и однородность явлений. Чем меньше показатель вариации, тем более процесс устойчивый, а значит, и более предсказуемый.
Показатели вариации отражают не отдельно взятые значения, а дают характеристику некоторому явлению или процессу в целом. Имея в наличии показатели среднего значения и вариации, можно получить первичное представление о характере данных. Средняя – это обобщающий уровень, а вариация характеризует, насколько среднее значение (или другой показатель) хорошо обобщает значения некоторой совокупности данных. Если показатель вариации незначительный, то значения совокупности находятся близко к среднему, следовательно, среднее значение хорошо обобщает совокупность. Если вариация большая, то среднее значение плохо обобщает данные (значения разбросаны далеко друг от друга), и получается «средняя температура по больнице».
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.
Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Межквартильный размах
В статистике для анализа выборки часто прибегают к другому показателю вариации – межквартильному размаху. Квартиль – это то значение, которые делит ранжированные (отсортированные) данные на части, кратные одной четверти, или 25%. Так, 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данных пополам (то бишь медиана), ну и 3-й квартиль отделяет 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями. У данного показателя есть одно неоспоримое преимущество: он является робастным, т.е. не зависит от аномальных отклонений.
Наглядное отображение размаха вариации и межкварительного расстояния производят с помощью диаграммы «ящик с усами».
Среднее линейное отклонение
Есть показатели вариации, которые учитывают сразу все значения, а не только отдельные наблюдения (типа максимума или минимума). Одним из таких является среднее линейное отклонение. Этот показатель характеризует меру разброса значений вокруг их среднего. В чем суть? Для того, чтобы показать меру разброса данных, нужно вначале определиться, относительно чего этот самый разброс будет считаться. Обычно это среднее арифметическое. Далее нужно посчитать, насколько каждое значение отклоняется от средней. Нас интересует среднее из таких отклонений. Однако напрямую складывать положительные и отрицательные отклонения нельзя, т.к. они взаимоуничтожатся и их сумма будет равна нулю. Поэтому все отклонения берутся по модулю. Средне линейное отклонение рассчитывается по формуле:
a – среднее линейное отклонение,
X – анализируемый показатель,
X̅ – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
Рассчитанное по этой формуле значение показывает среднее абсолютное отклонение от средней арифметической. Наглядная картинка в помощь.
Отклонения каждого наблюдения от среднего указаны маленькими стрелочками. Именно они берутся по модулю и суммируются. Потом все делится на количество значений.
Для полноты картины нужно привести еще и пример. Допустим, имеется фирма по производству черенков для лопат. Каждый черенок должен быть 1,5 метра длиной, но, что еще важней, все должны быть одинаковыми или, по крайней мере, плюс-минус 5 см. Однако нерадивые работники то 1,2 м отпилят, то 1,8 м. Дачники недовольны. Решил директор провести статистический анализ длины черенков. Отобрал 10 штук и замерил их длину, нашел среднюю и рассчитал среднее линейное отклонение. Средняя получилась как раз, что надо – 1,5 м. А вот среднее линейное отклонение вышло 0,16 м. Вот и получается, что каждый черенок длиннее или короче, чем нужно, в среднем на 16 см. Есть, о чем поговорить с работниками.
На этом сегодняшнюю заметку закончим. В следующей статье будут рассмотрены такие показатели вариации, как дисперсия, среднеквадратичное отклонение и коэффициент вариации.
Средние величины и показатели вариации
Понятие и виды средних величин
Существует 2 класса средних величин: степенные и структурные.
К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.
Степенные средние величины
Степенные средние могут быть простыми и взвешенными.
Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:
Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида, которые будут далее подробно рассмотрены.
Средняя арифметическая
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической простой: (3+4+4+5)/4 = 16/4 = 4.
Средняя арифметическая взвешенная имеет следующий вид:
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической взвешенной: (3*1 + 4*2 + 5*1)/4 = 16/4 = 4.
Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X отсутствует нижняя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.
Средняя арифметическая применяется чаще всего, но бывают случаи, когда необходимо применение других видов средних величин. Рассмотрим такие случаи далее.
Средняя гармоническая
Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:
Средняя геометрическая
Средняя геометрическая применяется при определении средних относительных изменений, о чем сказано в теме Ряды динамики. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.
Средняя квадратическая
Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.
Главной сферой применения квадратической средней является измерение вариации значений X, о чем пойдет речь позднее в этой лекции.
Средняя кубическая
Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.
Структурные средние величины
К наиболее часто используемым структурным средним относятся статистическая мода и статистическая медиана.
Статистическая мода
Если X задан дискретно, то мода определяется без вычисления как значение признака с наибольшей частотой. В статистической совокупности бывает 2 и более моды, тогда она считается бимодальной (если моды две) или мультимодальной (если мод более двух), и это свидетельствует о неоднородности совокупности.
Если X задан равными интервалами, то сначала определяется модальный интервал как интервал с наибольшей частотой f. Внутри этого интервала находят условное значение моды по формуле:
где Мо – мода;
ХНМо – нижняя граница модального интервала;
hМо – размах модального интервала (разность между его верхней и нижней границей);
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующего модальному;
fМо+1 – частота интервала, следующего за модальным.
Если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.
Статистическая медиана
Если X задан дискретно, то для определения медианы все значения нумеруются от 0 до N в порядке возрастания, тогда медиана при четном числе N будет лежать посередине между X c номерами 0,5N и (0,5N+1), а при нечетном числе N будет соответствовать значению X с номером 0,5(N+1).
Если X задан в виде равных интервалов, то сначала определяется медианный интервал (интервал, в котором заканчивается одна половина частот f и начинается другая половина), в котором находят условное значение медианы по формуле:
где Ме – медиана;
ХНМе – нижняя граница медианного интервала;
hМе – размах медианного интервала (разность между его верхней и нижней границей);
fМе – частота медианного интервала; 
Также как и в случае с модой, при определении медианы если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.
Показатели вариации
Размах вариации
Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:
Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.
Cреднее линейное отклонение
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4. Рассчитаем среднее линейное отклонение простое: Л = (|3-4|+|4-4|+|4-4|+|5-4|)/4 = 0,5.
Вернемся к примеру про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4 и среднее линейное отклонение простое = 0,5. Рассчитаем среднее линейное отклонение взвешенное: Л = (|3-4|*1+|4-4|*2+|5-4|*1)/4 = 0,5.
Линейный коэффициент вариации
С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.
В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, линейный коэффициент вариации составит 0,5/4 = 0,125 или 12,5%.
Дисперсия
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил оценки: 3, 4, 4 и 5, ранее уже была рассчитана средняя арифметическая = 4. Тогда дисперсия простая Д = ((3-4) 2 +(4-4) 2 +(4-4) 2 +(5-4) 2 )/4 = 0,5.
В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию взвешенную: Д = ((3-4) 2 *1+(4-4) 2 *2+(5-4) 2 *1)/4 = 0,5.
Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию методом разности средней квадратов и квадрата средней:
Д = (3 2 *1+4 2 *2+5 2 *1)/4-4 2 = 16,5-16 = 0,5.

Cреднее квадратическое отклонение
Выше уже было рассказано о формуле средней квадратической, которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:
Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:
В примере про студента, в котором выше рассчитали дисперсию, найдем среднее квадратическое отклонение как корень квадратный из нее:
.
Квадратический коэффициент вариации
В примере про студента, в котором выше рассчитали среднее квадратическое отклонение, найдем квадратический коэффициент вариации V = 0,707/4 = 0,177, что меньше критериального значения 0,333, значит вариация слабая и равна 17,7%.
Показатели вариации в статистике
7.1. Абсолютные и относительные показатели вариации
Рассмотрим две совокупности сотрудников рекламных агентств.
Распределение сотрудников первого агентства по уровню месячной заработной платы представлено в табл. 7.1.
| Размер месячной заработной платы, руб. | Середина интервала, xi | Число сотрудников, чел., fi | xi*fi |
|---|---|---|---|
| 4 000-6 000 | 5 000 | 10 | 50 000 |
| 6 000-8 000 | 7 000 | 6 | 42 000 |
| 8 000-10 000 | 9 000 | 19 | 171 000 |
| 10 000-12 000 | 11 000 | 26 | 286 000 |
| 14 000-16 000 | 15 000 | 10 | 150 000 |
| 16 000-18 000 | 17 000 | 5 | 85 000 |
| Сумма | — | 95 | 1 031 000 |
Распределение сотрудников второго агентства по уровню месячной заработной платы представлено в табл. 7.2.
| Размер месячной заработной платы, руб. | Середина интервала, xi | Число сотрудников, чел., fi | xi*fi |
|---|---|---|---|
| 1 500-4 500 | 3 000 | 9 | 27 000 |
| 4 500-7 500 | 6 000 | 26 | 156 000 |
| 7 500-10 500 | 9 000 | 24 | 216 000 |
| 10 500-13 500 | 12 000 | 18 | 216 000 |
| 13 500-16 500 | 15 000 | 14 | 210 000 |
| 16 500-19 500 | 18 000 | 10 | 180 000 |
| 19 500-22 500 | 21 000 | 9 | 189 000 |
| Сумма | — | 110 | 1 194 000 |
Рассчитаем средний уровень заработной платы:
Как видим, средние в двух совокупностях практически совпадают между собой (с разницей в 1 руб.). Однако если вы вдруг случайно встретите сотрудников этих агентств и поинтересуетесь уровнем оплаты их труда, то вас заверят, что платят у них вовсе не одинаково! Почему?! Оказывается, что разброс значений вокруг средней в этих совокупностях абсолютно разный. Значит, такой характеристики, как средняя, вовсе не достаточно, чтобы делать выводы о совокупности. Для этого используют показатели вариации.
Вариацией называется изменчивость значений признака у единиц статистической совокупности. Для измерения величины вариации используются абсолютные и относительные показатели вариации.
Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака
 | ( 7.1) |
Среднее линейное отклонение (d) представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от их средней. Если данные не сгруппированы, то рассчитывается невзвешенное среднее линейное отклонение
 | ( 7.2) |
Для сгруппированных данных, представленных в виде вариационного ряда, используется взвешенное среднее линейное отклонение, где весами выступают частоты соответствующих вариант:
 | ( 7.3) |
Дисперсией (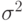
 | ( 7.4) |
 | ( 7.5) |
Квадратный корень из дисперсии называется средним квадратическим отклонением (его называют также стандартным отклонением):
 | ( 7.6) |
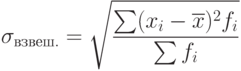 | ( 7.7) |
Для сравнения вариации одного и того же показателя в разных совокупностях (например, заработной платы двух рекламных агентств) или вариации разных показателей в одной совокупности (например, вариации заработной платы и возраста в одном рекламном агентстве) используют относительные показатели вариации. К ним относят:




















 .
.